提高初中生利用“一元二次方程”解决实际问题能力的教学研究
广西北流市沙垌镇初级中学 岑平海
在初中数学中,“一元二次方程”是一个非常重要的学习内容,特别是用它来解决实际生活当中的问题,非常有效,而且只要熟练掌握,可以为我们的生活带来极大的方便。然而,“一元二次方程”对初中学生而言又是一个比较难学的数学内容,因此老师需要通过故事引导激发学生学习兴趣、举一反三提高学生应变能力、挖掘现实引导学生学以致用这三个步骤,来培养和提高初中生运用“一元二次方程”解决实际问题的能力。
本文以人教版九年级上学期的数学课本为参考,分析如何提高初中生利用“一元二次方程”解决实际问题的能力。
一、故事引导,激发学生学习兴趣
爱听故事是每个人的天性,对初三的学生而言,随着他们学习压力进一步增大,像数学中“一元二次方程”这样比较难学且枯燥的内容,他们的学习兴趣往往会受到压制,因此我们可以通过形式各样的数学故事,来引起他们对“一元二次方程”的关注,激发他们的学习兴趣。故事教学法有利于为学生创设趣味的学习情境,使学生产生强烈的求知欲,从而提高学生自主探索、创造、思考的能力。
如在讲解“一元二次方程”时,我们可以为学生讲解关于“一元二次方程”由来的故事:方程这个名词最早见于中国古代数学著作《九章算术》,它成书于东汉末年,书中记录了246个实际应用问题的计算解决方法。《九章算术》一共分为九章,“方程”是其中的一部分,对于“方程”的解释,中国古代数学家刘徽作了经典注释:“程,课程也。二物者二程,三物者三程,皆如物数程之,并列为行,故谓之方程。”这里所说的“如物数程之”意思是指“有几个未知数,就需要列出几个等式”。对于一次方程组而言,因为它每个未知数的系数如果用“算筹”(一根根同样长短和粗细的小棍子)来表示,就如同方阵,因此被称作是“方程”。
在《九章算术》勾股章中的第20题,有这样一个问题:“今有邑方不知大小,各中开门,出北门二十步有木,出南门十回步,折而西行一千七百七十五步见木。问邑方几何。”用今天的话说,大意是:如图1,DEFG是一座正方形小城,北门H位于DG的中点,南门K位于EF的中点,出北门20步到A处有一树木,出南门14步到C,再向西行1775步到B处,正好看到A处的树木(即点D在直线AB上),小城的边长为 步。
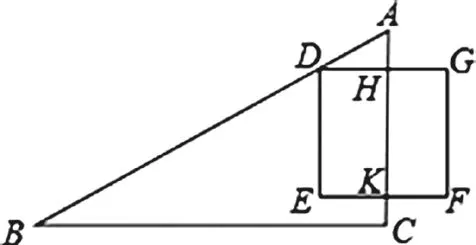
图1
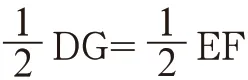
提示:因为△AHD、△ACB它们都是直角三角形,所以它们是相似三角形,这里我们可以用到初中八年级所学到的知识“相似三角形比例关系公式”,即如果两个三角形是相似三角形,其中一个三角形的三边分别为A、B、C,另一个三角形的三边为M、N、X,那么我们可以得到A:M=B:N=C:X。然后再结合我们学习到的一元二次方程的知识,这道题是不是很容易求解呢?
总结:这道题看起来很难,但是经过分析我们发现,只要我们充分利用好“相似三角形比例关系公式”和“一元二次方程”的相关知识,这道题就会迎刃而解。通过这道题,既可以让学生从故事中感受到我国古人的高度智慧和才华,感受到中华民族的伟大,也锻炼了他们运用“一元二次方程”知识解决实际问题的能力。
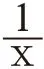
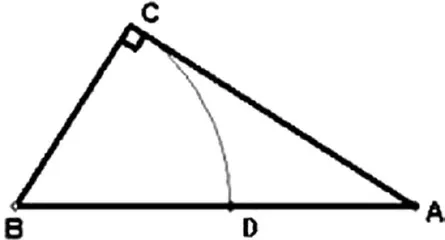
图2
总之,通过关于“一元二次方程”故事的引入,可以让学生知道“一元二次方程”的起源、发展、衍变过程,认识到历代数学家曾经在对这个问题上进行了无数努力,付出了辛勤的汗水,激励学生们树立一种锲而不舍的数学探究精神,并引发他们对数学科学的浓厚兴趣,提高他们对“一元二次方程”的应用能力。
二、举一反三,提高学生应变能力
在学习初中数学时,举一反三、灵活变通是学生必备的一种数学思维和解题能力,这对于提高学生的数学素养、巩固他们的数学基础,有着十分重要的作用。那么,在初中数学课堂教学过程中,该怎样培养学生应用“一元二次方程”解决实际问题的“举一反三”能力呢?这就要求老师善于对问题进行归类,让他们在解决实际问题过程中,既能够掌握基本的理论知识,做到“知其然”,又掌握到类似问题的解题思路和方法,做到“知其所以然”,让他们跳出原来的思维束缚,对同类问题能够举一反三,提高解题效率和准确度。
对于一元二次方程应用题而言,主要有四个类别:增长率问题、行程问题、经济问题、工程问题,不同类别的题目都有相应固定的解题思路和方法,但解题的步骤万变不离其宗,都有六个步骤:(1)仔细审题,明确题意;(2)找出已知量和未知量以及相等关系;(3)设未知数;(4)用所设未知数表示相关的量;(5)列等式;(6)解方程;(7)检验所得的根是否符合题意和实际要求。
如这样一个题目:某商店购进一种商品,进价30元,试销中发现这种商品每天的销售量P(件)与每件的销售价X(元)满足关系:P=100-2X,若商店每天销售这种商品要获得200元的利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
分析:很明显这是一个关于“一元二次方程”的经济问题求解,题目中已经给出了一个等量关系:P=100-2X,因此我们可以围绕这个关系来找到解决问题的突破口。已知量:进价30为元,每天的利润为200元,未知量:每件的售价,每天售出的件数。
提示:利润=售价-进价,总利润=单件商品利润×所售商品件数
解题思路和过程:我们可以设每件的售价为x元,那么每天的销售量则为(100-2x)件,单件的利润为(x-30),所以总的利润为(x-300)(100-2x)元,因此我们可以得到一元二次方程:(x-300)(100-2x)=200,经过整理得到:x-350x-15000=0,解这个方程即可得到答案。需要注意的是100-2x≥0,x≥0,所以x的取值范围是0≤x≤50。
当老师引导学生把上述题目解决后,可以再出一道同类型的题目,让学生经过独立思考进行解答,从而培养他们举一反三的数学解题能力。
如:某商店将进价为8元的商品按每件10元售出,每天可销售200件,现在采用提高商品售价减少销售量的办法增加利润,如果这种商品按每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
分析:这也是一个关于“一元二次方程”的经济问题,已知量:进价8元,提高售价前的售价为10元,销售件数为200件,总利润为640元,并且还知道每件的销售价每提高0.5元其销售量就减少10件,未知量:提高售价后每件商品的定价。
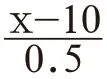
同样的,关于“一元二次方程”的增长率问题、行程问题、工程问题,我们也可以通过同类题型的归纳总结,训练学生“举一反三”用数学解决实际问题的能力。
三、挖掘现实,引导学生学以致用
培养和提高初中生利用“一元二次方程”解决实际问题的能力,实际上是锻炼初中生对数学科学知识“学以致用”的能力。学以致用,对初中生而言是一个十分重要的学习应用技能。初中生在生理上正处于青春发育期,这一时期他们的最大特点是:生理上蓬勃成长、急骤变化,智力迅速发展,情绪和情感的内容十分丰富,心理的稳定性也在逐步提高。因此,培养和提高他们“学以致用”的能力,可以为他们今后的学习和生活,乃至人生发展奠定非常重要的基础。
数学作为一门基础性的学科,和我们的日常生活息息相关,“学以致用”的需求性更强,因此老师在讲解“一元二次方程”问题时,要特别注意从现实生活中挖掘有意思的数学问题,和“一元二次方程”挂钩,从而提高初中生利用“一元二次方程”解决实际问题的能力。
如有这样一个问题:微信红包是沟通人们之间感情的一种方式,已知小明在2016年“元旦节”收到微信红包为300元,2018年为675元,若这两年小明收到的微信红包的年平均增长率为x,根据题意可列方程为________。
分析:很明显这是一个关于“一元二次方程”增长率的数学应用问题,同时和我们日常生活紧密相关。已知量:2016年和2018年元旦收到的红包钱数分别为300元、675元,并且题目已经设出了未知数x(增长率),因此这个问题很好解决。
提示:增长率=增量/原总量*100%
解题思路和过程:增长率为x,2016年元旦节的红包为300元,那么2017年元旦节的红包为300(1+x)元,2018年元旦节的红包为300(1+x)元,因此我们可以列出等式:300(1+x)=675。
除了微信红包问题,新冠肺炎更是当今社会关注的热点话题,我们可以将其和“一元二次方程”数学问题紧密结合起来。如:有一个人患了新冠肺炎,经过两轮传染后共有169人患了新冠肺炎,每轮传染中平均一个人传染了____个人。
分析:这是一个关于“一元二次方程”的传播问题,已知量:两轮传染后新冠肺炎的感染人数,未知量:平均一个人传染的人数。
提示:一元二次方程传播问题公式 为:a(1±χ)=b,a为 基 准 量,也就是变化之前的量;b为变更量,即:变化之后的量;χ为增长率(也可以为降低率,此时χ前面是负号)。
解题思路和过程:设平均一个人传染的人数为x人,那么第一轮传染后的总人数为(1+x)人,第二轮传染后的总人数为(1+x)人,因此可以得到等式:(1+x)=169,解得x=12(取正值),因此每轮传染中平均一个人传染了12个人。
四、结语
总之,利用“一元二次方程”解决实际问题是初中生必须要掌握的重要技能之一,只要我们通过故事引导、举一反三、紧密联系现实这几种常用的数学教学方法,就能够提高初中生对于“一元二次方程”问题的学习兴趣,提高他们举一反三、学以致用的数学应用思维和能力,为他们今后的学习和生活打下坚实的基础。希望通过我们全体数学老师的共同努力,继续探索更多、更好、更加创新的利用“一元二次方程”解决数学实际问题的数学教学方案,从而提高初中数学的教学水平和质量。

