基于起重船的海上风机整机吊装动力响应分析*

刘永平 杨乐楠 苑桂博 陈明胜

(1.保利长大工程有限公司 广州 51010； 2.武汉理工大学船海与能源动力工程学院 武汉 430063)

我国海上风能资源丰富，可利用海域面积300多万 km2，5～25 m水深的近海领域内，风电可装机容量2亿kW[1]。截至2020年底，我国海上风电产业并网装机容量已达5×106kW以上[2-3]。海上风电安装船需求大，而国内自升式海上风机安装船资源缺乏，浮式起重船以其船源充足、使用费率低、不受水深限制等优点被广泛应用于海上风电安装作业。与自升式风机安装船相比，起重船依赖锚泊系统定位，受风浪流等外部环境影响产生的运动较大，出于安全和经济考虑，有必要在施工之前使用数值仿真方法预报起重船、风机和锚链耦合系统的运动和重要结构受力，为实际施工提供参考。

鲁华伟[4]在国内首次采用模型试验的手段进行系泊-大型起重船-索具-大型上部组块耦合系统运动响应特性及其机理的研究，用试验手段验证了之前对于吊物耦合系统运动响应特性的猜想。方田等[5]考虑吊物提升对船舶重心的影响，开展了不同海况下起吊作业动态连续过程的时域运动模拟研究，分析了起吊作业过程中船舶运动变化规律，以及船舶和吊重摆动的相互影响。将体积较大、形状复杂的风机简化为体积小、形状规则的吊物或质点进行研究有一定的局限性，有必要对风机进行建模与起重船耦合进行动态响应分析，朱明等[6-7]考虑吊索的弹性变形，建立了6自由度的船舶模型和5自由度的风机模型，对起重船和风机的耦合多体动力学模型采用数值仿真的方法分析系统的动力响应。

本文以 “长大海升”3 200 t起重船为研究对象，使用海洋工程分析软件AQWA模拟海上风机整体式吊装作业。首先建立起重船、平衡梁、风机机组，以及风机基础的边界元模型，对自由漂浮状态下起重船进行水动力分析。然后对边界元模型施加约束条件，如吊索、护弦、系泊系统等，建立多体耦合模型。最后分别对静态悬吊风机工况和风机与基础对接作业进行时域模拟，揭示海洋环境和吊放速度对船舶运动、风机运动、对接碰撞次数，以及碰撞力的影响规律。

1 计算理论

频域水动力计算使用基于格林定理的边界元法。在满足自由表面、结构湿表面、海底表面和无穷远处表面边界条件的情况下，求解每个面元上的速度势，然后根据线性伯努利方程推导出船舶受到的水压力，沿船舶湿表面积分，得到波浪激励力、附加质量，以及辐射阻尼系数，并求解频域运动方程得到响应幅值算子(RAO)，频域运动方程如下。

[-ω2(Ms+A(ω))-iωBs(ω)+

(1)

时域计算根据频域计算得到的水动力系数，通过逆傅里叶变换，建立以Cummins方程为基础的系泊船舶时域耦合运动方程。

(2)

式中：A(∞)为无穷大频率下的附加质量矩阵；xs为船舶的位移；K(t)为脉冲响应函数；fs为船舶受到的外力，N；上标表示力的形式，exc为波激力，wind为风力，c为海流力，m为系泊力，cable为船舶受到的吊索拉力。

加速度脉冲响应函数矩阵由下式定义。

(3)

船舶和风机之间的吊索传递两者运动引起的吊索力，两者也通过吊索力耦合在一起。风机的运动方程可以表示为

(4)

式中：MO为风机质量矩阵；BO为施加给风机的阻尼矩阵；xO为风机的位移；fO为风机受到的外力，N;上标wind为风力，cable为吊索拉力，fender为风机与基础之间碰撞力，下标O为海上风机。

2 数值分析模型

“长大海升”号起重船和5 MW风机[8]主尺度见表 1。

表1 “长大海升”号和5 MW风机主尺度

使用AQWA-DM和AQWA建立起重船、风机、单桩和平衡梁的边界元模型。根据研究的侧重点，对模型进行了简化，假设船舶和吊臂是刚性结构，只建立对吊装过程动力响应影响较大的塔筒。使用AQWA中的Linear Cable模型模拟吊索，根据实船所用吊索设置刚度和预伸长量。系泊系统参数见表2。

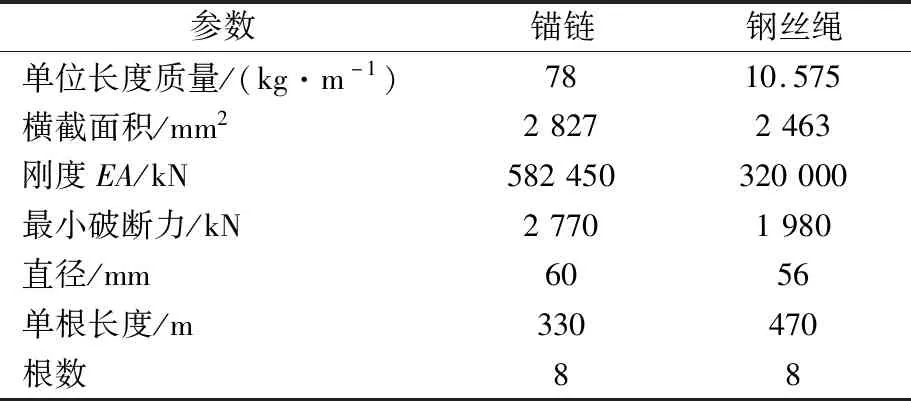
表2 系泊系统参数

使用Nonlinear Catenary模型建立两段式八字形锚泊系统。使用fender模块模拟平衡梁抱箍和单桩基础与风机的碰撞。整体仿真模型见图1。AQWA中风浪流的方向定义见图2。环境参数见表3，文中假设波浪、定常风、定常流同向。

图1 计算模型

图2 AQWA中方向定义

表3 环境参数

3 频域水动力分析

频域水动力分析模块中每间隔22.5°取1个浪向。本文主要计算不同浪向角时起重船的响应幅值算子(RAOs)。响应幅值算子通常用来表达自由漂浮状态浮体结构在单位波幅规则波下的频率响应特性，与波幅成正比。海上风机安装过程主要关注船舶横摇、纵摇和垂荡响应，运动响应结果见图3，假定船舶沿纵轴对称，选择分析的入射浪向分别为0°、45°、90°和135°。从图3中可知，“长大海升”号起重船的响应主要集中在0～-1 rad/s的频率范围内，横摇响应在0.66 rad/s出现峰值，纵摇响应在0.56～0.71 rad/s较大，垂荡响应在频率小于0.21 rad/s时较大，施工中应尽量避免这些波浪频率。

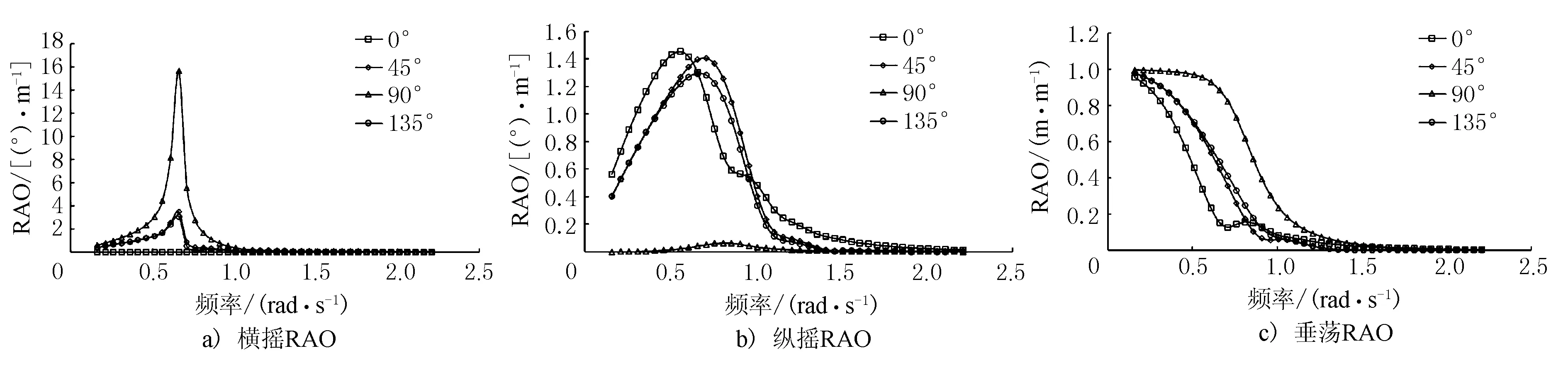
图3 “长大海升”号频域响应分析结果

4 运动响应时域分析

采用时域分析方法，在风浪流的共同作用下，对风机悬吊的静态工况和风机与单桩基础的对接工况进行数值模拟。时域计算模型整体包括船舶、系泊缆、吊索、风机、平衡梁和单桩。计算时间1 500 s，步长0.01 s。

4.1 静态工况下环境荷载方向的影响分析

1) 起重船运动。根据起重船和吊装作业的特性，主要关注垂荡、横摇和纵摇这3个自由度的运动响应，不同波浪入射角的运动数据见表4。

表4 船舶在不同波浪入射角下运动数据统计

由表4可见，船舶各自由度的运动对波浪入射角的敏感度不同，浪向角对垂荡的影响较小，横浪作用下响应最大；不同浪向下横摇运动幅度变化量较大，顺浪和迎浪下运动幅度较小，横浪下较大；斜浪下起重船纵摇运动幅度较大，横浪下较小。起重船进行吊装作业时，出于安全考虑，一般要求横倾角小于5°，纵倾角小于2°， “长大海升”号在横摇和纵摇方向最大运动峰峰值分别为1.01°和0.55°，均小于安全值。

2) 风机运动。风机在吊装过程中的运动类似单摆运动，主要关注横荡、纵荡、垂荡和纵摇这4个自由度的运动，运动响应值见表5。

表5 风机在不同波浪入射角下的运动数据统计

由表5可见，风机纵摇运动和起重船纵摇运动规律相似；随浪向角从横浪向迎浪或顺浪移动，风机横荡运动逐渐减小，而纵荡运动则相反，但是由于起重船的遮蔽，顺浪下纵荡运动比45°斜浪下小；风机垂荡运动在斜浪中最大，在横浪时最小，这主要是因为风机垂荡运动受起重船垂荡和纵摇的两方面的影响。

4.2 对接工况下碰撞

对接作业时，风机底座与单桩基础平台会发生碰撞，严重时会造成结构损坏。起重机把风机下放到一定高度后，由人工牵引靠近粗导向板，后沿着粗导向板下降，直到风机底座和单桩基础平台接触。在这个过程中，粗导向板起到限制风机水平平移和摇摆的作用，因此本文主要考虑垂荡方向运动。

1) 对接速度的影响。取0.00 2，0.006和0.01 m/s 3种不同的对接速度，分析风机与基础碰撞时的垂荡运动和碰撞力。参考S.J.Jung[9]等对海上平台安装桩腿钢对钢接触的模拟，在AQWA中使用4个fender模拟碰撞，设置fender的刚度为9.933×108N/m，长度为0.1 m，布置于单桩基础顶部平台，见图4。在确保精确度的情况下，设置时间步长为0.002 s。波浪方向为90°。

图4 Fender布置图

风机垂向位移和碰撞力见图5、图6，由于吊索的存在，起重船的运动影响着风机的垂荡运动，导致发生多次碰撞。不同吊速下的碰撞力见表6。由表6可见，在0.002，0.006，0.01和0.08 m/s的下放速度下，风机与基础平台的碰撞次数分别为9次、5次、5次和1次，最大碰撞力分别为1.22×106，1.27×106，1.57×106和1.43×106N。当发生多次碰撞时，第二次碰撞的碰撞力显著大于第一次碰撞，所以应尽量避免多次碰撞的发生。

表6 不同吊速下风机与基础平台的碰撞力

图5 不同对接速度下的风机垂向位移

图6 不同吊速下风机与基础平台的碰撞力

2) 波浪周期的影响。系泊船舶的各自由度运动对波浪周期的变化较为敏感，有必要研究不同波浪周期下风机的垂向位移和碰撞力的变化规律。在0.006 m/s的对接速度下，取波浪周期分别为5.5、6.5和7.5 s，不同周期下的风机垂向位移和碰撞力见图7、图8和表7。由表7可见，波浪周期为5.5、6.5和7.5 s时碰撞次数分别为1次、5次和9次，最大碰撞力分别为2.44×105、1.27×106和2.02×106N。显然，随着波浪周期的增大，碰撞次数增多，最大碰撞力也增大，实际施工时应尽量选择较小周期海浪环境下进行风机安装作业。

图7 不同波浪周期下的风机垂向位移

图8 不同波浪周期下风机与基础平台的碰撞力

表7 不同波浪周期下风机与基础平台的碰撞力

5 结论

本文采用基于势流理论的海洋工程软件AQWA对海上风机整体吊装作业进行仿真模拟，首先进行起重船的水动力分析，并对风机悬吊静态工况和对接工况进行时域分析。对波浪浪向角、波浪周期和对接速度进行了敏感性分析。

1) 根据频域水动力分析和静态工况时域模拟的计算结果可知，横摇、纵摇和垂荡RAO均有取得较大值的海浪频率范围，应避免在此范围内施工。同时起重船布置时应该尽量使船艏迎浪或者顺浪，避免波浪横向或斜向入射。

2) 风机垂荡运动和风机与基础的碰撞力受对接速度和海浪周期的影响显著。当对接速度较小或者海浪周期较大时，风机会与基础碰撞多次，第二次碰撞时碰撞力显著大于第一次碰撞，所以应尽量避免多次碰撞的情况发生，如难以避免，可在对接点配置缓冲器，防止结构损伤。同时随着对接速度增大或者海浪周期增大，最大碰撞力呈明显增大的趋势。