对2022年高考数学全国甲卷一道真题的解读

⦿河南省周口市淮阳红旗中学 余良涛

1 引言

众所周知，全国卷因覆盖面广、重基础、重能力而精彩，近几年它又注重对数学本质的考查，使之更具有探究性和挑战性，集中体现出了“活”的特点.高考命题始终坚持“源于课本，高于课本，不拘泥于课本”的命题导向.笔者在闲暇之余，意外发现了2022年一道高考试题在课本上的“影子”，现结合案例进行解读，以飨读者.

2 高考真题呈现

(2022年全国甲卷文科第14题) 设点M在直线2x+y-1=0上，点(3,0)和(0,1)均在⊙M上，则⊙M的方程为________.

3 真题解析

分析：设出点M的坐标，利用点(3,0)和(0,1)均在⊙M上，求出圆心及半径，即可得圆的方程.

解析：因为点M在直线2x+y-1=0上，所以不妨设点M坐标为(a,1-2a).

又点(3,0)和(0,1)均在⊙M上，则点M到点(3,0)和(0,1)的距离相等且为半径r.

整理，得a2-6a+9+4a2-4a+1=5a2.

解得a=1.

因此，⊙M的方程为(x-1)2+(y+1)2=5.

4 考题出处

笔者通过认真比对，惊奇地发现它的“影子”.它是源自普通高中课程标准实验教科书(必修)《数学2(A版)》(人民教育出版社，2007年2月第3版)第120页的例3.题目如下：

已知圆心为C的圆经过点A(1,1)和B(2,-2)，且圆心C在直线l：x-y+1=0上.求圆心为C的圆的标准方程.

分析：本题采用2022年全国甲卷的解法肯定是可行的，而教材的解法是采用几何性质法，即利用“圆中任意弦的垂直平分线必过圆心”“圆内的任意两条弦的垂直平分线的交点一定是圆心”，然后再利用两点间的距离公式求出半径r即可.笔者在这里就不再详细解答了，具体过程读者可参考课本例题的解答.

通过以上分析，我们不难发现，2022年全国甲卷这道高考试题是教材例3的“影子”.当然，2022年全国甲卷这道高考题也可采用教材例3的解法求解.笔者在这里真诚地希望读者要重视“影子”类问题，而教师也更应该重视“影子”类问题的教学.

5 变式探究

这种类型问题除了上述分析中提到的两种解法外，不妨试想一下它还有没有其他的解法？因此，我们可以放开手大胆探究一下.下面结合教材中的例3进行解读.

教材例3体现了是圆的标准方程的灵活应用，特别是要强调图形在分析问题中的辅助作用.我们知道确定一个圆的要素主要是圆心位置和半径长.借助图形再结合题设条件，发现这类问题的关键是找出圆心位置，圆心位置一旦确定，就可以利用距离公式求出半径r，从而再求解.

需要指出的是，在求线段AB的垂直平分线的方程时也可以不求线段AB的中点坐标与直线l′的斜率，而是根据线段垂直平分线的性质“线段垂直平分线上的点到线段两端点的距离相等”这一结论得到(x-1)2+(y-1)2=(x-2)2+(y+2)2，然后再经过化简整理可得直线l′的方程为x-3y-3=0.

请读者记住上述方法，以后我们再求圆的方程就可以采用以上三种方法解答，同时还要密切关注解法的灵活性.

6 自我提升

例题已知圆心C在直线x-2y-3=0上，且过点A(2,-3)和B(-2,-5)，求圆心为C的圆的标准方程.

解法1：待定系数法.

设所求圆的标准方程为(x-a)2+(y-b)2=r2.

由题设条件,可得

①

②

③

联立方程①②③，解得

a=-1,b=-2,r2=10.

故所求圆的标准方程为(x+1)2+(y+2)2=10.

解法2：几何性质法.

由圆心C在直线x-2y-3=0上，可设点C的坐标为(2t+3,t).

因为该圆经过A,B两点，所以|CA|=|CB|,即

解得t=-2.

故所求圆的标准方程为(x+1)2+(y+2)2=10.

解法3：几何性质法.

所以，弦AB的垂直平分线的方程为y+4=-2x，即2x+y+4=0.

又圆心C是直线2x+y+4=0与x-2y-3=0的交点，易解得交点坐标为(-1,-2).

所以，圆心C坐标为(-1,-2).

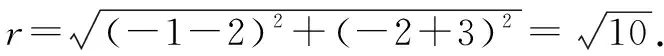
故所求圆的标准方程为(x+1)2+(y+2)2=10.

点评：此题是“一题多解”类问题，通过求解后发现，“待定系数法”思维简单，运算量较大，但此法易于理解掌握.而“几何性质法”略显抽象，掌握起来有一定难度，此法需结合圆的有关性质进行考虑，如垂径定理等.但这两种解法备受命题人青睐，请读者一定要掌握.

你真的掌握了吗？下面两个题目读者不妨尝试一下.

(1)(2001年全国高考题改编)过点A(1,-1)，B(-1,1)且圆心在直线x+y-2=0上的圆的方程是.

分析：对于求解圆的方程问题，我们首先要善于挖掘题设条件中隐含的几何要素，即圆心坐标和半径长，但圆心坐标的确定是难点，通常确定圆心位置在弦的垂直平分线上、直径的中点上或中心对称点上等等，再利用两点间距离公式求半径长即可.

(2)(2019年甘肃酒泉中学二模)已知圆M与直线x-y=0及x-y+4=0都相切，且圆心在直线y=-x+2上，则圆M的标准方程为.

分析：根据题设条件很容易想到设出圆心M的坐标，然后利用圆心M到两直线距离相等，建立等量关系式，求出圆心M的坐标，从而解出圆M的半径即可.

上述两个题目，请读者自行完成.可以结合本文所述的内容，做好解题反思，因为它们都具备一定的“模型化”和“套路化”的特点，所以以后要注意“影子”类问题，深刻理解，灵活把握，从而达到“举一反三”的效果.

7 解读启示

通过以上解读，我们知道数学因“问题”而生，探究因“问题”而明，课堂因“问题”而精彩.笔者建议教师要做到：课前带着“问题”精备，课上带着“问题”精讲，课后带着“问题”精练，促使“问题”式探究教学法贯穿教学始终，有效穿插“一题多解”“一题多变”“一题多问”“一题多联”等多种解题方法的灵活运用，稳步提高教学效果.