坐标方法终有时 蝴蝶万态醉题中*——从四个视角研究2022年全国高考数学甲卷理科第20题

⦿四川省双流中学 曹军才 李莎莎 耿晓琦

解析几何的基本研究方法就是坐标法，即用代数方法研究几何问题.对一道具体题目的研究，需要思考如何用坐标或方程表达点和线，即如何将几何问题代数化，实现“从几何中来”；也需要研究题目背后隐藏的东西，即问题本身或解决途径可否类比、迁移，实现“到几何中去”.贾德(Charles H.Judd)的一项早期实验表明：一切教育的目的都是在发展系统的思想，这种思想能从它被获得的情境中迁移到别的情境中去[1].下面以2022年全国高考数学甲卷理科第20题为例，从几个视角谈谈从“解题”到“解决问题”[2]的系统认知.

1 问题再现

(2022年全国高考数学甲卷理科第20题)设抛物线C:y2=2px(p>0)的焦点为F，点D(p,0)，过F的直线交C于M，N两点．当直线MD垂直于x轴时，|MF|=3．

(1)求C的方程；

(2)设直线MD,ND与C的另一个交点分别为A,B，记直线MN,AB的倾斜角分别为α,β．当α-β取得最大值时，求直线AB的方程．

2 问题分析

第(2)小题思维导图如图1.

图1

思路1:以直线斜率为参数，由线及点.

思路2：以点的坐标为参数，由点及线.

设出点M,N,A,B的坐标，由四点所满足的直线方程MN,MA,NB,AB的统一结构，通过直线经过定点寻得坐标积的定值关系，进而发现两直线MN,AB斜率的关系.

思路3：以角度为参数，由角及形.

已知条件中有直线倾斜角，因此可以写出直线的参数方程并代入抛物线方程，借助参数t表达点、线.

思路4：以直线系方程入手，由线及形.

题目中有四条直线，其中MN过定点(1,0)，MA,NB过定点(2,0)，因此可以从过定点的直线系方程入手解答，优化思路1的多次联立直线与抛物线方程.

思路5：以动态图形寻定点，由静制动.

抛物线中有四边形ABMN且其对角线的交点为定点，图形形似蝴蝶，联想蝴蝶定理，借助几何关系，猜证结合，辅助代数推理.

思路6：以动态图形寻定线，由形释数.

由蝴蝶图形的对称性，MB,NA在x轴上下方的对称位置的交点纵坐标互为相反数、横坐标相同，猜想直线MB,NA的交点轨迹是一条垂直于x轴的定直线.

3 问题解决

图2

(一)视角一：通法.

(2)通法1：如图2，设直线MN:x=my+1.由(1)知，曲线C的方程为y2=4x.设M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4).

所以y3=2y2.同理可得y4=2y1.

又因为直线MN，AB的倾斜角分别为α,β，所以

则Δ3>0,y3y4=-4n=4y1y2=-16，得n=4.

另解(求直线AB方程)：当α-β最大时，

又因为y3y4=4y1y2=-16，所以

点评：这是中学生熟悉的解析法——线参法，即含参直线和二次曲线相交，联立方程，获得关键方程，再用韦达定理获得交点的坐标关系，是通法.难点是如何寻求直线AB与MN的斜率关系，只能边算边看.此题坐标法运用自然，突出解析几何的基本分析方法，摒弃了弦长、范围等套路问题.

通法2：设M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4)，则

又因为直线MN过定点(1,0)，所以y1y2=-4.

同理,直线MA的方程为4x-(y1+y3)y+y1y3=0，直线NB的方程为4x-(y2+y4)y+y2y4=0.

又因为直线MA，NB都经过定点(2,0)，所以

同理，直线AB的方程为4x-(y3+y4)y+y3y4=0.

点评：这也是中学生熟悉的解析法——点参法，即设出点的坐标，利用点在曲线上，则点的坐标就满足相应曲线方程，进而注意到抛物线中任意弦所在的直线方程具有对称的统一结构.此法也是通法，较通法1更为简洁.

t2sin2α-4tcosα-4=0.

设M,N对应的参数分别为t1,t2,则

下同通法1.

点评：这也是中学生熟悉的解析法——角参法，即引入角作参数，利用直线参数方程求解.

下同通法1.

点评：借助过定点的直线系，获得点的坐标关系.

(二)视角二：溯源.

图3

蝴蝶定理如图3,设D为圆内弦PQ的中点，过点D作弦MA,NB，设MN,AB分别交弦PQ所在直线于点X,Y，则D是XY的中点.

注：① 点D在圆内是不必要的，可以在圆外；

② 圆可以改为任意圆锥曲线.

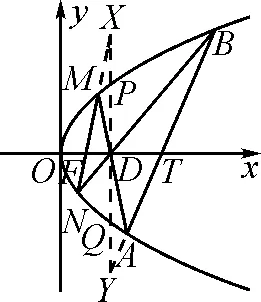
图4

解法5：如图4,过点D作直线DQ垂直于x轴，交MN于点X，交AB于点Y，交抛物线于P,Q两点.因为|PD|=|QD|，所以由蝴蝶定理可知|XD|=|YD|.

设直线AB交x轴于点T，则

下面证明直线AB过定点T.

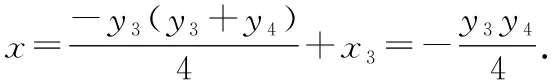
所以|DT|=4-2=2，从而tanα=2tanβ.

下同通法1.

点评：蝴蝶翩翩，形态万千.借助蝴蝶定理猜想直线AB过定点T，进而需要寻求y1y2与y3y4的关系.目标明确，思路清晰.

图5

解法6：如图5,设直线MN与AB交于点Q(x,y).

由通法2可知，直线MN的方程为

4x-(y1+y2)y+y1y2=0①

直线AB的方程为4x-(y3+y4)y+y3y4=0，即

4x-2(y1+y2)y+4(y1y2)=0

②

①×2-②，得4x+2y1y2-4(y1y2)=0.

所以4x=2y1y2=-8，即x=-2.

故交点Q的轨迹是定直线x=-2.

设此直线交x轴于点H，要使α-β最大，即使∠FQT最大.

问题转化为在定直线x=-2上取一点Q，使张角∠FQT最大.

显然，当HQ与△FQT的外接圆相切于点Q时，满足条件.

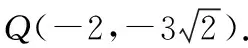
点评：此法是该题的一种几何解释，转化后的问题“张角∠FQT最大”即为米勒问题(最大视角问题).其实，极点(x0,y0)关于曲线y2=2px的极线就是y0y=p(x+x0)，则极点D(2,0)关于曲线y2=4x的极线就是0·y=2(x+2)，即定直线HQ：x=-2.

(三)视角三：拓展.

反思1:此题中F,D可定位于x轴上任意点.当然，F,D也可定位于形内其他位置.

变式设M,N,A,B为抛物线y2=2px(p>0)上任意四点，MN,AB交x轴于F,T，MA,BN交于点D.设F(a,0)，D(b,0)，MN,AB的倾斜角分别为α,β，当α-β取最大值时，求直线AB的方程.

解：设M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4)，直线MN的方程为x=my+a.

y1+y2=2pm，y1y2=-2pa

③

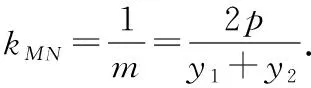
所以y1y3=-2pb.同理，可得y2y4=-2pb.

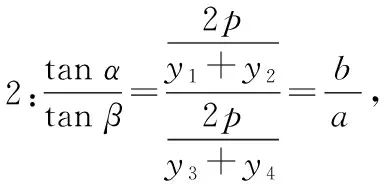
点评：点F,D确定，直线AB过定点是蝴蝶定理蕴含的一个结论.令p=2,a=1,b=2，即为原题及其解答.

(四)视角四：推广.

反思2：原题可以推广至椭圆中.当然，也可以推广到其他圆锥曲线中.

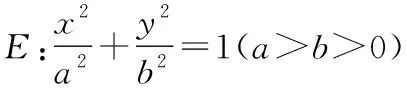
(1)求椭圆E的方程；

图6

分析：本题第(1)问过程略，第(2)问有如下3种解法.

解法1:不妨设A(x1,y1),B(x2,y2)，且y1>0，如图6.

(3m2+4)y2+6my-9=0.

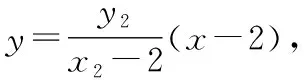
所以

图7

因为MO//XF，所以

又FY//ON，所以

图8

点评：此题中蝴蝶定理的运用尽显其优越性，解法2，3较解法1，运算简洁，近乎秒杀！

对试题的研究，贵在迁移，形成知识链，进入命题意境.从通法角度研究各种解法固然重要，此为“境”；但若能从溯源题目出处、拓展题目结论、推广题目类型等视角，揣测命题者想法，更能从一定高度审视题目，此为“意”.身在高考试题的“境”中，达其“蝴蝶定理”之“意”，悟数学之美妙，通数学之本真.