竖直平面内的圆周运动模型解析

王世超

(山东省沂南第一中学)

竖直平面内的圆周运动是高中阶段物理各类考试中最常考的题型,是高考考查的重点,而且常以大分值的计算题形式出现.它之所以会成为高考考查的重点和热点,是因为想要解决这类问题,就需要掌握牛顿运动定律、动能定理、功能关系等主要知识点,还要对临界状态分析、数形结合等物理思想有较深入的理解,对学生的综合能力和学科素养有较高要求.因此,我们有必要对这一题型做深入分析.

1 题型特征总结

1.1 常见模型

1)轻绳模型

如图1所示,运动物体在一轻绳的作用下绕固定点在竖直平面内做圆周运动,该模型的最大特征是物体运动过程中轻绳只能提供拉力,无法提供支持力.对轻绳模型2种情况总结如下.

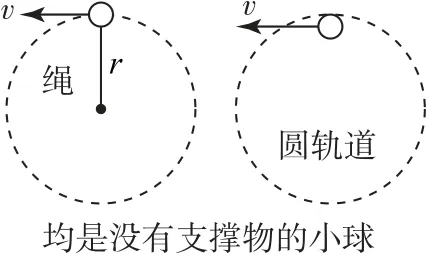
图1

a)临界条件分析.

由mg＝可得物体过最高点的临界条件是,故有物体能过最高点时,v≥v临＝;物体不能达到最高点时,v＜v临＝

b)最高点和最低点分析.

在最高点有2种情况:一是轻绳或圆轨道对物体仍有力的作用,提供向心力,有F＋mg＝,其中F是轻绳或者圆轨道对物体的弹力.二是轻绳或圆轨道对物体无力的作用,不提供向心力,有mg＝

在最低点只有一种情况,即轻绳或圆轨道对物体有力的作用,提供向心力,则有F－mg＝

c)在最高点F-v2图像如图2 所示(以竖直向下为正方向).

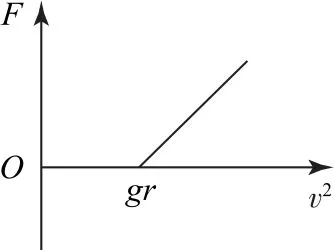
图2

2)轻杆模型

如图3所示,运动物体在一轻杆的作用下绕固定点在竖直平面内做圆周运动,该模型的最大特征是物体运动过程中杆对物体有支持力和拉力作用,物体过最高点时所受合力可以为零,在最高点能够处于平衡状态.

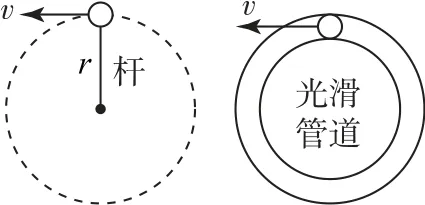
图3

a)临界条件分析.

由于有轻杆的支持力作用,物体过最高点时临界速度v临＝0.

b)最高点和最低点分析.

在最高点可能有4种情况:

Ⅰ.当v＝0时,轻杆或圆轨道对物体竖直向上的支持力等于物体的重力,即F＝mg,支持力F的方向沿半径背离圆心.

Ⅱ.轻杆或圆轨道对物体无力的作用,只有物体的重力提供向心力,即mg＝,有v＝.

Ⅲ.当,轻杆或圆轨道对物体有拉力作用,拉力和物体的重力提供向心力,有F＋mg＝,拉力F的方向沿半径指向圆心,大小随v的增大而增大.

Ⅳ.当时,物体的重力大于其所需的向心力,轻杆或圆轨道对物体有向上的支持力,有mg－F＝,支持力F的方向沿半径背离圆心,支持力F的大小随v的增大而减小.

在最低点只有一种情况:轻杆或圆轨道对物体有竖直向上的力的作用,有F－mg＝

c)在最高点F-v2图像如图4所示(以竖直向下为正方向).

图4

1.2 方法点拨

物理模型是物理问题最基本的提炼.我们遇到的问题不可能完全按照物理模型进行设计,但熟练掌握基本模型的知识原理,能帮助我们以不变应万变.

1)解题步骤

a)审题,确定研究对象;b)分析研究对象的运动情况,即确定研究对象的速度、运动半径、圆周运动的圆心等;c)受力分析,确定向心力的来源;d)列式,可根据牛顿运动定律、功能关系等列式;e)求解、讨论,避免计算错误或漏掉某些情况.

2)解题思路

“两点一过程”:“两点”即上面提到的最高点、最低点,根据对两点的受力分析,寻找向心力来源,根据牛顿第二定律等列方程;“一过程”是指在研究某个过程中运用能量观点(机械能守恒定律、动能定理)列方程.

2 典型例题解析

例“水流星”是杂技表演中较受欢迎的表演项目,已知“水流星”由两个水桶和一根刚性绳组成,将水桶拴在绳子两端,在水桶中装满水,杂技演员握着绳子将它甩动起来,两水桶就会如流星般飞舞,即便水桶口竖直朝下了,桶里的水也不会流出一滴.图5-乙是某一时刻水流星位置示意图,水桶A在最高点,水桶B在最低点,杂技演员只需控制绳子中点O位置不动,水桶A和B恰好能通过最高点.已知绳长l＝1.6m,两水桶的质量(包括桶和桶里的水)相等,均为m＝0.5 kg,不计空气阻力和绳子的重力,g取10m·s－2.求:

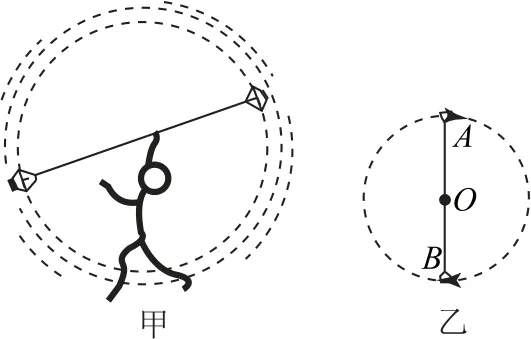
图5

(1)在最高点和最低点水桶的速度大小;

(2)图乙状态时,手对绳子的力的大小.

分析本题是最典型的竖直面内的圆周运动,属于轻绳模型.该题难度不大,只需要应用牛顿第二定律、机械能守恒定律,结合受力分析和向心力表达式,就能完成解题.

解(1)设在最高点和最低点水桶的速度分别为v1和v2.由题意知水桶做圆周运动的半径

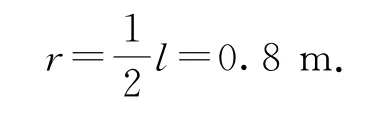
由题中“水桶A和B恰好能通过最高点”一句可知,当水桶通过最高点时,绳子对桶没有拉力,桶和水的重力提供向心力,即mg＝,代入数据解得

根据机械能守恒定律,当水桶由最高点运动到最低点时,有mgl＋,代入数据解得

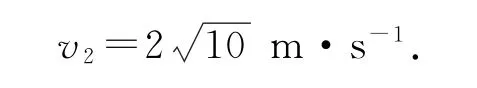
(2)由题意可知,绳OA对水桶A没有力的作用,绳子OB对水桶B有力的作用,水桶B做圆周运动的向心力由绳子的拉力FOB和水桶的重力的合力提供,以水桶B为研究对象,受力分析得FOB－mg＝代入数据解得FOB＝30N.

3 总结

竖直平面内的圆周运动是牛顿运动定律和功能关系综合考查的最好结合点,与该模型相关的大都是圆周运动、平抛运动、多体运动的综合问题,甚至还会涉及电场和磁场的相关知识,看似繁杂,解题思路和方法却很简单,那就是先确定研究对象,确定不同运动的衔接点和运动状态,然后利用相关公式列式即可.对于竖直平面内的圆周运动,一定要先确定是轻绳模型还是轻杆模型,然后根据我们总结的知识结合题意分析即可.对于瞬时状态(如最高点和最低点)应用牛顿运动定律解答;对于过程(如两点的联系)应用功能关系(如动能定理、机械能守恒定律)解答.

(完)