近刚性圆柱水下爆炸气泡动力学特性研究

黎一锴，席儒

（北京理工大学 机械与车辆学院，北京 100081）

气泡广泛存在于自然现象及工程应用中，例如空化气泡产生的空蚀效应[1-2]，水下炸药爆炸所产生的爆炸气泡对海底结构产生冲击作用[3-4]，超声波清洗中产生的声空化泡在特定区域的溃灭会剥除边界上污垢[5-7]. 很多学者对气泡和不同类型的边界之间的相互作用进行了大量的实验研究，比如刚性边界[8-10]，弹性边界[11-12]，自由液面边界[13-14]等. 汪浩等[15]对水下爆炸气泡的脉动载荷和气泡溃灭高速射流对内加筋圆柱壳结构的毁伤机理进行了计算分析.ZHANG 等[16]对刚性圆柱体附近的脉动气泡的动力学特性做了详细的实验研究，实验展示了不同参数条件下气泡的丰富形态变化.

数值模拟可以提供更多实验中无法观测的流场细节. GONG 等[17]采用了边界积分法（BIM）研究了火花产生的气泡与弹性橡胶之间相互作用的物理行为. 该方法基于势流理论，在无粘不可压缩流体域边界上求解流场，模拟结果与实验结果达成较好的一致性. Li 等[18]基于有限体积法在OpenFOAM 中开发了一个计算模型来研究水下爆炸气泡和自由液面耦合的动力学特性，该模型基于可压缩两相流求解器结合流体体积法（VOF）捕捉气液界面，很好地验证了实验中自由液面表面尖刺，气泡坍缩过程中射流及气泡分裂合并等动力学现象. 夏冬生等[19]采用VOF 多相流模型对近平面固壁微米尺度空化泡的溃灭进行了数值研究，研究表明空泡与固壁的量纲一的距离对固壁的空蚀破坏机理有着重要影响.

气泡的脉动过程是一个高度非稳态、非线性的过程，平面边界相对于气泡脉动过程是一个封闭边界，而圆柱形边界相对于气泡脉动过程则是一个半封闭边界，因此圆柱形边界的存在对气泡脉动过程中的形态、射流速度、气泡质心的偏移等需要进一步的研究.

文中采用数值模拟并借助实验验证的方法研究刚性圆柱附近脉动气泡的动力学特性. 为了研究气泡与刚性圆柱之间的相互作用，采用电容水下放电产生气泡的实验方法，并用高速摄像机捕捉气泡和刚性圆柱相互作用下的形态变化. 基于Navier-Stokes方程并结合VOF 方法捕捉气液两相界面，模拟脉动气泡在刚性圆柱附近的动力学特性. 文中的研究结果将丰富气泡-复杂边界相互作用机制的理论.

1 实验设置

实验设置如图1 所示. 实验在一个边长为30×30×30 cm 的立方玻璃水箱中进行. 直径为3 mm 的刚性圆柱右端固定在水箱上，气泡通过控制电容器的充放电产生. 充电过程中，采用220 V 的电源对电容为2 200 μF 的电容进行充电. 在放电过程中，当电容器两端电压达到120 V 时，信号发生器发生信号，放电电路接通，电容器产生高能量，一对直径为0.1 mm的铜线在接触点被熔断. 瞬间的高温使得铜线交点处液体蒸发成气体，铜丝接触点即为初始气泡的中心，通过控制接触点的初始位置来控制气泡到圆柱表面的距离. 采用这种方法所产生的气泡最大半径为5 mm±0.2 mm. 由于尺寸差异较大，细铜线对气泡和刚性圆柱相互作用的影响可以忽略不计.

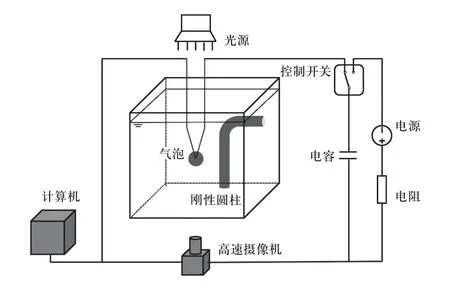
图1 实验装置Fig. 1 Experiment setup

文中采用高速摄像机捕捉气泡的瞬态演化过程.相机帧率为17 021 fps，曝光时间为4 μs. 实验采用LED 灯为相机拍摄提供光源. 所有实验均在大气压（约0.1 MPa）和室温（约25oC）下进行.

2 物理模型和数值方法

2.1 物理模型

气泡和刚性圆柱之间的距离参数如图2 所示. 图中S*为气泡型心到圆柱表面的水平距离；Sh为气泡初始中心到圆柱表面的水平距离，则在初始时刻有：S*=Sh；Rm为气泡的最大半径. 并取水平线与刚性圆柱的左侧交点为观测点A.

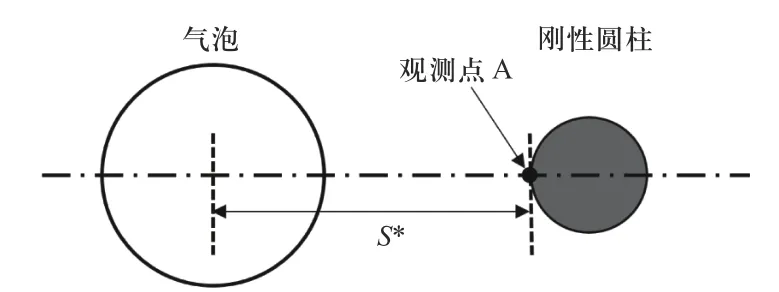
图2 气泡-刚性圆柱距离参数示意图Fig. 2 Schematic diagram of the distance between bubble and rigid cylinder

由于刚性圆柱的存在，气泡在膨胀过程中理论上与刚性圆柱存在三种不同的相对位置关系，包括无接触，刚好接触和过度接触三种. 不同的相对位置关系下气泡与圆柱之间的耦合作用显然是不一样的，为了量化气泡与圆柱之间的相对位置关系，文中引入了一个量纲一的参数γ=Sh/Rm来表示气泡与圆柱之间的相对距离.

2.2 数值方法

根据文中研究所对应的物理模型，文中在Fluent 软件计算环境中，采用气-液两相流方法进行数值模拟.为求解文中所对应的两相流问题，数值计算采用欧拉-欧拉法. 在欧拉-欧拉法中，不同的相被处理成相互贯穿的连续介质，各相的体积不能被其他相占据，且各相的体积分数之和为1，不同的相均满足守恒方程. 在本文中，流体第一相为液态水，第二相为水蒸气. 假定气泡内部气体为可压缩的水蒸气，气泡周围的液体为不可压缩牛顿流体. 并假定气相和液相不相混，不考虑气体在气-液界面的扩散. 由于实验中产生的气泡尺寸较小并且气泡存在时间很短，所以不考虑重力的影响. 此外，忽略气体的冷凝和蒸发. 流动状态视为层流.

2.2.1 控制方程

文中基于N-S 方程并结合VOF 模型对刚性圆柱附近水下爆炸气泡的脉动过程进行数值计算，气泡的运动由控制方程决定. 整个流场的连续性方程、动量和能量方程为

文中采用流体体积法（VOF）来跟踪欧拉网格中的气-液两相界面. VOF 方法通过各相流体在每个网格中所占的体积分数来追踪并重构界面，这里引入标量函数c跟踪两相界面，并利用对流方程计算：

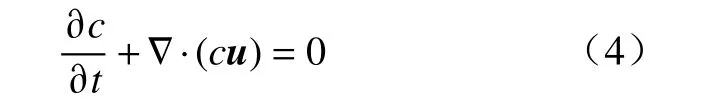
式中：c为体积分数，c=0和c=1分别为气相和液相，而0 ＜c＜1表示气液界面.

混合流体的物理性质包括密度和黏度作为各相的体积分数的函数来计算：

2.2.2 计算域和计算方法

文中数值模拟采用二维对称模型，计算域及边界条件如图3 所示. 计算域为半圆区域，基于ICEM CFD 软件对计算域分块，并删除刚性圆柱所对应的模块，留下的半圆弧即对应于刚性圆柱壁面，位于气泡右侧. 计算域整体采用结构化O-型网格划分. 计算域底部为对称边界条件，半圆弧壁面指定为滑移边界条件. 计算域上侧圆弧为压力出口边界条件. 计算域半径为50 倍最大气泡半径，以减小压力边界对气泡和刚性圆柱之间相互作用的影响. 气泡放置在对称轴线上，其初始气泡中心与圆柱表面距离为Sh. 由于整个计算域相对气泡尺寸较大，为了能够准确捕捉到气泡的动力学特性，对气泡附近区域进行网格加密，如图中虚线框所示. 经过网格无关性分析，最小网格尺寸为50 μm×50 μm.

图3 计算模型Fig. 3 Calculation model

计算中压力-速度耦合采用压力的隐式算子分裂算法（PISO）. 密度项、动量项和能量项采用二阶迎风格式，以提高计算精度. 梯度项采用基于网格单元的最小二乘格式，流体体积分数离散格式采用Geo-Reconstruct 格式，压力项采用PRESTO 离散格式，时间项采用一阶隐式格式. 时间步长取固定时间步长0.1 us，以保证CFL 数低于0.2.

2.2.3 初始条件

气泡的初始条件包含气泡的初始半径R0、初始压力P0、初始温度T0. 文中假定初始气泡为一个充满饱和蒸汽的零速度的高温高压球型气泡，内部压力场和温度场均匀. 一般来说，数值模拟中的初始半径R0应当尽可能地接近实验中初始气泡的半径. 因为初始气泡半径设定过大则会丢失气泡初始膨胀阶段产生的速度和压力场分布，这将降低数值模拟的精确度. 然而若采用很小的初始半径，一方面意味着我们需要采用足够小的网格分辨率来捕捉初始气泡的变化，另一方面，由于气泡产生的初始时刻内部气体物理性质缺乏足够的实验数据，气泡内部流体的状态是否与传统流体状态一致无法确定[21].

本实验所产生的气泡最大半径大约为5 mm，由于气泡的最大半径与初始条件密切相关，为使得数值模拟结果和实验结果达成一致，采用Rayleigh-Plesset 方程以及试错法确定R0及P0，T0为饱和蒸汽在P0下对应的饱和温度. 最终确定气泡初始半径为0.3 mm，初始压力为11.6 MPa，初始温度为596K 的初始条件得出的结果与实验结果达成很好的一致.

3 结果和分析

3.1 实验验证

图4 为气泡与刚性圆柱相互作用的第一个周期以及气泡二次回弹的过程.Sh=4.5 mm，最大气泡半径Rm=5 mm ，γ=0.9.

图4 气泡的轮廓随时间的演变(γ=0.9)Fig. 4 The evolution of the bubble's outline over time (γ=0.9)

在图4（a）中膨胀阶段，由于气泡和壁面距离较大，所以初始膨胀气泡呈现为对称的球形. 随后气泡右侧的膨胀受到刚性圆柱的抑制而变得扁平，同时气泡左侧自由膨胀呈现半球形（第3 帧）. 此时注意到气泡在膨胀坍缩的第一个周期下与圆柱表面始终存在一层薄薄的液膜间隙，这说明气泡在这个阶段始终没有与圆柱接触. 在第7 帧图片中发现了坍缩的过程中气泡的右侧形成了一个锯齿状的裙部，用箭头指明了出来. 气泡在收缩过程中被横向地拉长，以至于在产生射流之前有较大的横纵比. 在图4（a）的最后两帧，文中观察到气泡向刚性圆柱的表面产生强烈的冲击.

图4（b）显示了对应的数值模拟的结果，在气泡膨胀阶段及坍缩阶段的初期，气泡与圆柱表面存在一层液膜. 第7 帧显示了气泡在坍缩过程形成了锯齿状的泡壁，用箭头表示了出来. 第9 帧图片显示气泡在坍缩过程末期形成了射流，并且射流从气泡左侧贯穿到气泡右侧，这导致了环形气泡的产生. 由于射流宽度很小，实验结果中很难清晰地看到射流的存在，但是气泡对圆柱表面的冲击说明了射流的客观存在，而数值模拟的结果很好地再现了射流产生和发展. 图5 中给出了气泡等效半径数值模拟结果和实验结果随时间的变化对比图，总体上保持一致.数值结果与实验结果一致表明数值模型很好地再现了气泡与刚性圆柱之间的相互作用.

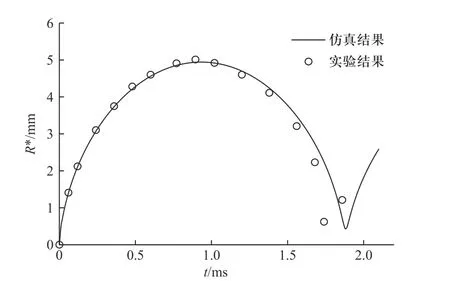
图5 气泡等效半径仿真和实验结果对比图Fig. 5 Comparison of simulation and experimental results of bubble equivalent radius

3.2 流场分析

图6 给出了数值模拟中一些关键时刻的速度场和压力场. 每幅图像被对称地分成两部分. 上部分是速度场和速度矢量场，下部分是压力场. 气泡界面用黑色实线表示，白色部分代表刚性圆柱. 如图6（a）所示，初始阶段气泡与刚性圆柱之间距离相对较大，所以气泡初始膨胀时呈现球型. 由于气泡体积的迅速增加，气泡内部的压力显著降低. 在气泡的大部分寿命中，气泡内部的气体压力要低于周围介质的压力.因此气泡在膨胀阶段气泡壁的移动并不是完全由内外压力差控制，而是由流体的惯性主导. 从图6（b）中可以清楚地看到气泡在坍缩阶段出现锯齿状泡壁的物理机制. 气泡坍缩阶段时外界液体在绕过圆柱表面朝向气泡流动时，圆柱的上下侧形成了速度梯度.图7 给出了刚性圆柱中心垂直线（图6（b）中黑色粗实线）上的速度v与壁面表面距离Y*的关系，靠近圆柱表面的液层有着较大的绕流速度，这部分液层冲击气泡壁形成上下对称的两个凹坑，这使得气泡右侧在收缩过程中呈现锯齿状. 在图6（c）中可以观察到高速水射流形成以及射流贯穿整个气泡的情况.从压力场看到气泡的左侧形成了局部高压区，而气泡内部的压力场分布是均匀的. 因此气泡的左侧坍缩速度要更快，在高压区作用下形成一股向右的液体射流.射流继续增长并穿透气泡，气泡在坍缩到最小体积的过程中分裂成左右两个部分，如图6（d）所示.

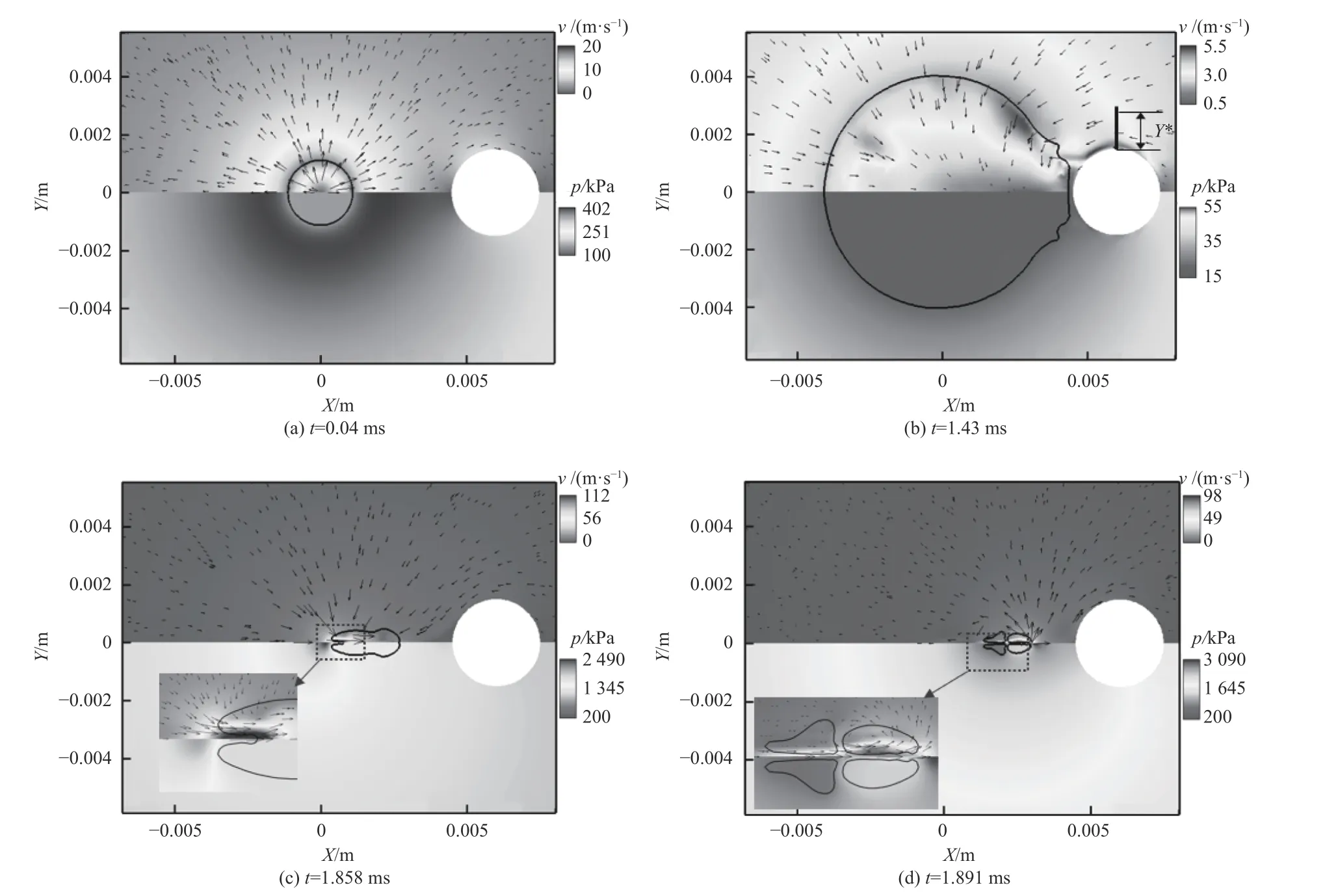
图6 速度和压力场(γ=0.9)Fig. 6 Velocity and pressure field (γ=0.9)

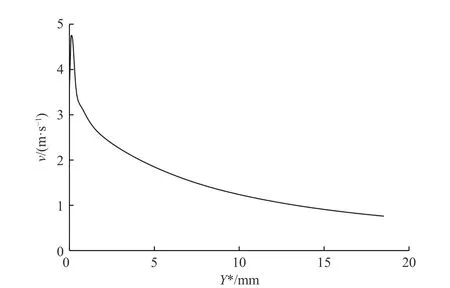
图7 刚性圆柱中心垂直线上速度与表面垂直距离Y*的关系Fig. 7 The relationship between the velocity on the vertical line of the rigid cylinder center and the vertical distance Y* from the surface of the cylinder

3.3 距离参数的影响分析

在气泡初始条件不变的情况下，改变 γ分别为0.5,0.8,1.1. 通过分析计算结果得到在气泡坍缩过程中不同 γ下观测点A的压力随时间变化过程曲线如图8 所示.

由图8 可见，观测点A处的压力首先随时间的增加缓慢增高，这是由于气泡在收缩的过程中气泡左侧的压力逐渐增大，推动气泡往右侧移动，因此A点的压力逐渐增高. 随后气泡产生射流冲击圆柱表面，A点的压力急剧升高，并且当气泡距离圆柱越近时，冲击所产生的压力越大. 随着 γ的增加，射流产生的冲击逐渐减小，同时由于相对距离增加，射流冲击圆柱壁面的时间也在逐渐增大.

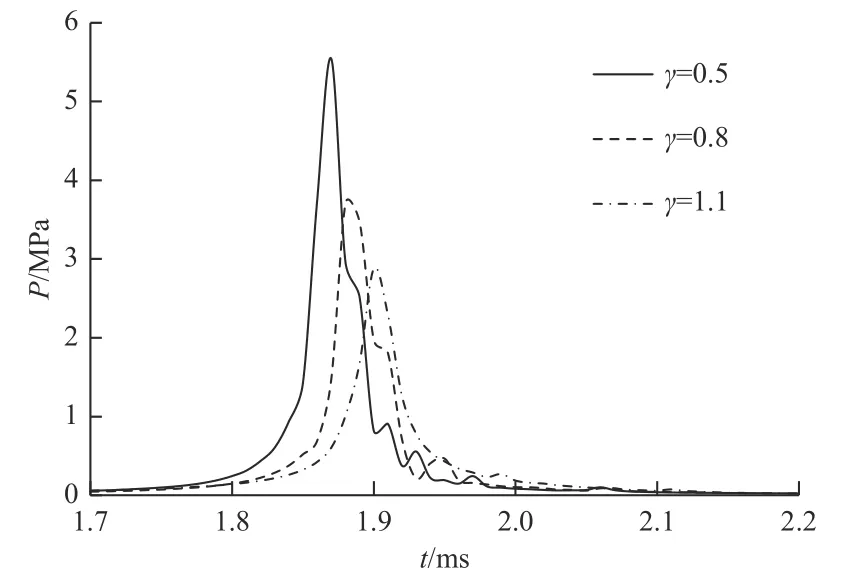
图8 不同 γ下观测点A 压力随时间的变化Fig. 8 Change of pressure at observation point A with time under different γ

图9 给出了观测点A的最大压力及气泡坍缩过程中最大射流速度umax随 γ的变化情况. 由图可以看出，测点A的最大压力随 γ的增加而减小，最大射流速度随着 γ的增加呈现先增大后减小的变化趋势. 当γ较小时（ γ＜0.9），随着气泡与壁面距离增加，气泡坍缩阶段周围液体压缩气泡时受到刚性圆柱的阻碍作用降低，气泡的压缩量增加，导致气泡壁的收缩速率加快，这将使得射流前泡壁的基础收缩速率增加，同时气泡左侧的局部高压区压力增大，将进一步使得气泡凹陷速度增加，最大射流速度变大. 此时虽然最大射流速度增大，但是最大射流产生的位置距离A点也相应的增加，气泡和圆柱中间液层的缓冲作用使得A点的最大压力依然减小. 当 γ继续增加时，最大射流速度存在一个最大值，之后减小. 这是因为气泡与壁面之间距离较远时，虽然气泡受到周围液体的压缩量增加，气泡壁运动速率加快，但是此时气泡左右两侧的动量差将减小，这将直接降低射流左侧的局部高压区产生的压差，进而降低最大射流速度.而此时A点的最大压力由于距离的增加不断减小.

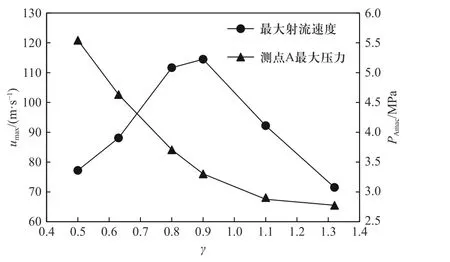
图9 最大射流速度及测点A 最大压力随 γ的变化Fig. 9 Variation of maximum jet velocity and maximum pressure of point A with γ

图10 给出了不同 γ下，水平方向上气泡型心与刚性圆柱表面的距离S*随时间的变化关系.由图中可以看出，在气泡膨胀阶段， γ较小的情况下（0.5 和0.63）曲线略微上涨，而在 γ较大的情况下S*的值保持不变，这是因为当气泡距离圆柱较近时，气泡的右侧在膨胀时很快受到圆柱的阻碍而变得扁平，而气泡的左侧自由膨胀，所以气泡的型心会略微远离圆柱. 当气泡与圆柱的距离较远时，气泡左右两侧膨胀速率差异不大，而当气泡右侧接近圆柱而变得扁平时，气泡左侧膨胀速率已经大为降低，因此总体上S*保持恒定. 在气泡坍缩阶段时，在气泡左右侧的压差下会使得气泡整体向右侧移动，同时由于射流的产生进一步地使得减小

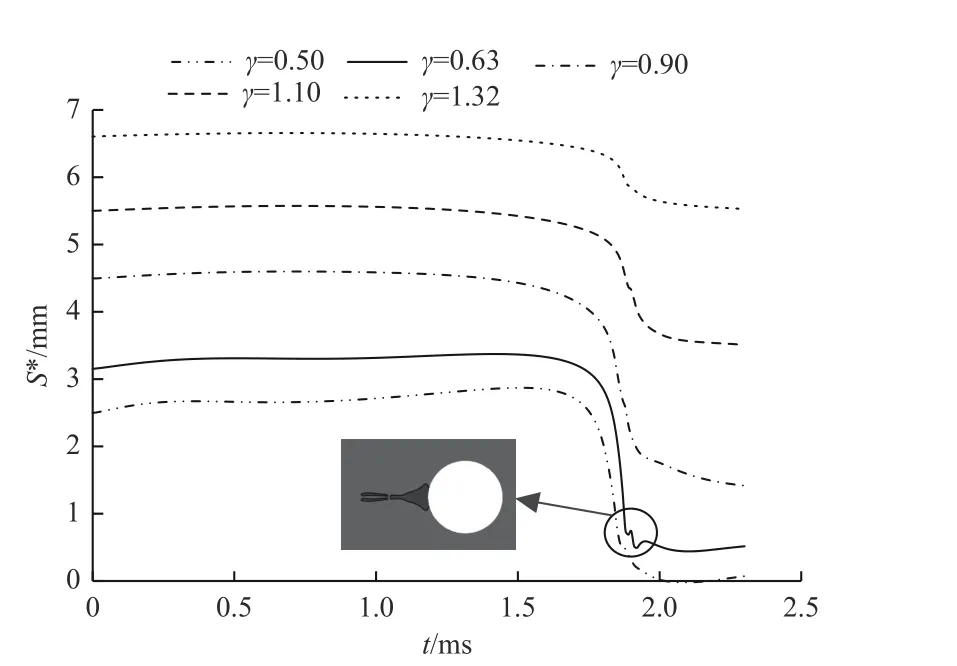
图10 不同 γ下气泡质心与刚性圆柱表面水平距离随时间的变化Fig. 10 Variation of the horizontal distance between the mass center of bubble and the surface of the rigid cylinder with time under different γ

在图10 中注意到，当 γ越小时，气泡质心在坍缩阶段向右侧偏移的程度越大，S*降低得更快. 当 γ=0.63 时S*在降低的过程中略微地回涨了一段距离，我们在图中用虚线框内标出. 这是由于气泡在坍缩的过程中分裂成了左右两个部分，然而由于左侧气泡部分较小，所以S*回涨的程度并不大. 当气泡在二次回弹阶段时，S*值又会略微地增加，这样的情况在γ越小的时候越明显.

4 结 论

文中基于Navier-Stokes 方程结合流体体积法（VOF）建立了近刚性圆柱水下爆炸气泡的数值模型，通过流场分析以及改变距离参数 γ研究了气泡的动力学特性. 主要结论如下.

①通过分析压力及速度场可以得出，水下爆炸气泡在脉动过程会使刚性圆柱表面流体介质存在速度梯度，速度较大的流体液层冲击气泡表面，致使气泡在收缩过程中呈现丰富的形态变化. 在气泡坍缩到最小时，气泡左侧会产生局部高压区，进而形成射流.

②气泡溃灭时射流对圆柱壁面冲击产生的压力随着 γ的增加而降低. 而最大射流速度随 γ的增加先增大后减小，在 γ=0.9 时射流速度最大.

③气泡型心的移动随 γ的不同变化显著. 在γ较小的情况下（ γ＜0.63），气泡在膨胀阶段型心略微左移；当 γ＞0.63 时，气泡型心在膨胀阶段几乎不变.同时 γ越大，气泡坍缩阶段型心的移动距离越小.