基于改进对比源反演算法的脑卒中微波检测成像技术研究

刘珩，王若璇

（北京理工大学 信息与电子学院, 北京 100081）

脑卒中是一种具有高病发率、高致残率、高死亡率的急性脑血管疾病，是导致中国人口死亡的主要疾病之一[1]，据调研2018 年中国脑血管疾病已造成157 万人死亡[2]. 目前国内对脑卒中检测的方式主要有CT 扫描、X 射线摄影、MRI 成像等[3],然而这些检测手段存在着检测设备庞大且昂贵、检测时间长、多存在辐射危害等缺陷，不仅为患者带来了巨大的经济负担，甚至可能因为错过救治的“黄金3 小时”从而给患者带来不可逆转的伤害[4]. 因此，快速、准确、有效的脑卒中检测方式和血块定位方法是救治脑卒中的关键.

针对脑卒中检测现状并结合微波技术特点，国内外学者开始研究利用微波检测脑卒中的新技术.微波检测技术依赖于不同组织之间介电对比度的存在[5]，具有使用安全，成像用时短，设备造价低廉且便于携带等优点，可应用于乳腺癌、脑卒中等病症的检测中. 近年来国内外也出现了大量关于将微波成像技术应用于脑卒中检测的研究，所涉及到的微波成像技术包括Born 近似迭代法[6]、微波共焦成像法[7]、对比源反演成像法[8-9]、模式识别算法[3，10-11]等，关于微波检测成像系统搭建的研究也层出不穷[12-14].2016 年，ISMAIL 等[9]首次提出将基于对比源反演(contrast source inversion, CSI)方法的微波成像技术应用于对大脑中血块的成像检测中，并取得了良好的成像效果.

然而由于CSI 算法收敛速度较慢，导致成像的时间较长. 为了提高成像的速度，本文提出一种改进的对比源反演算法-FCG-CSI 算法，用于出血性脑卒中的微波检测成像，利用快速共轭梯度法(fast conjugate gradient, FCG)替代常规共轭梯度法进行目标函数的优化，从而加快CSI 算法的收敛. 建立脑卒中微波检测成像系统，仿真实验包括利用多物理场仿真软件COMSOL 进行脑部模型的建立、设计天线进行微波信号的收发的模拟并采集相应的微波数据、利用FCG-CSI 算法对收集到的数据进行反演成像.成像结果表明，FCG-CSI 算法相比于CSI 算法成像时间更短、成像精确度也更高.

1 脑卒中微波检测成像整体框架

脑卒中微波检测系统采用电磁逆散射的成像方法，如图1 所示，系统可分为电磁散射正问题与电磁散射逆问题两部分. 其中正问题是在已知入射场和对比度函数的情况下，计算求解空间中的总电场与散射场分布[15]. COMSOL 软件是一款基于有限元法进行多物理场仿真计算的专业软件，本文将利用COMSOL 仿真软件进行电磁散射正问题的仿真求解，计算得到脑部周围的电场分布，并对微波数据进行采集、处理与存储；电磁散射逆问题根据入射场与计算得到的散射场，并通过重建算法反演人脑内部结构. 由于逆散射问题是非线性且不适定的[15]，求解难度很大，因此重建算法的选择对成像结果至关重要.本文利用一种改进的对比源反演算法-FCG-CSI算法对微波数据进行反演成像.

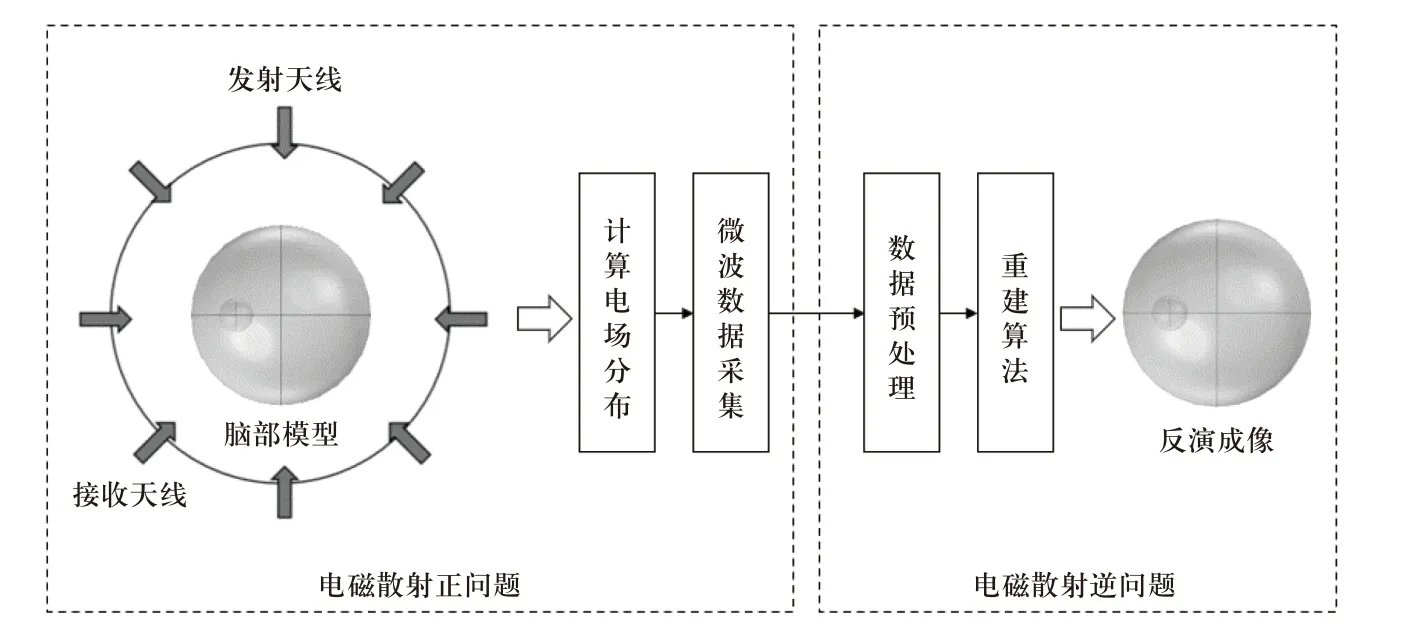
图1 脑卒中微波检测成像系统结构Fig. 1 Structure of microwave imaging system for stroke detection

2 成像算法

2.1 CSI 算法基本理论

考虑如图2 所示的电磁逆散射模型. 假设在一个复介电常数已知的均匀背景介质中，有一形状、大小、复介电常数均未知的散射体存在于有界且单连通的目标区域D. 发射天线与接收天线按如图2 所示的圆形轨道分布在目标区域D周围，发射天线数量为j，构成测量区域S. 本文考虑在TM 极化的条件下，此时散射场可表示为[16]

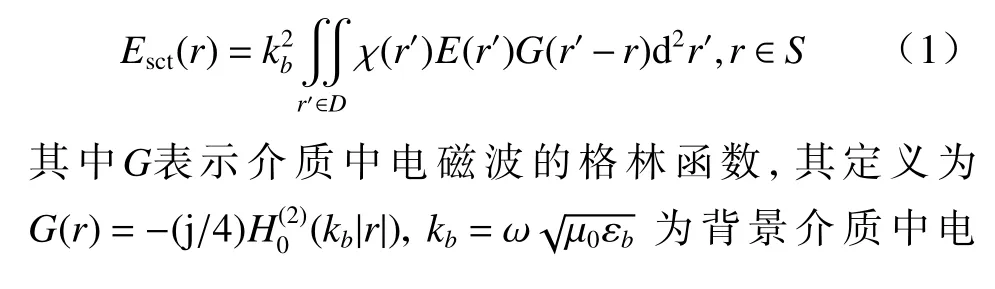
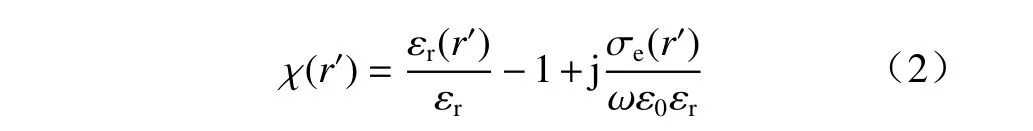
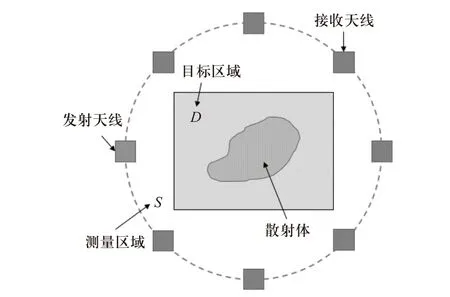
图2 电磁逆散射问题示意图Fig. 2 Schematic diagram of electromagnetic inverse scattering problem

在以上积分方程中，式(1)被称为“数据”方程，式(3)被称为“目标”方程[17]. 为了可以在算法中更加简洁且紧凑地表示“数据”与“目标”方程，引入对比源的概念，其为对比度与总电场的乘积，定义为w(r′)=χ(r′)E(r′)，这样便可将“数据”方程和“目标”方程简写为积分算子的形式，即

对比源反演(CSI)算法采用常规共轭梯度法（即P-R 共轭梯度法）对代价函数进行迭代优化，从而不断更新对比源与对比度.

乘法正则化对比源反演（multiplicative regularized contrast source inversion，MR-CSI）算法是在CSI 算法的基础上加入乘法正则化项FDTV(χ)，其代价函数为[16]

2.2 FCG-CSI 成像算法

在脑卒中微波检测成像技术中，MR-CSI 算法具有良好的成像效果，但由于常规CSI 算法应用的PR共轭梯度法收敛速度较慢，从而导致反演成像效率较低，耗时较长. 为了加快MR-CSI 算法的收敛速度，进一步提高算法的反演成像效率，本文在MR-CSI 算法的基础上，利用快速共轭梯度法（FCG）来替代常规共轭梯度法来进行代价函数的优化，由此来加速代价函数的收敛.

在常规MR-CSI 算法中，采用的是常规共轭梯度法，即PR（Polak-Ribiere）共轭梯度法来更新对比源.而在FCG-CSI 算法中，首先需将对比源wj,n-1进行一定的处理，以下用参数qj,n-1来表示经处理后的对比源wj,n-1. FCG-CSI 算法中对比源的迭代公式为[18]

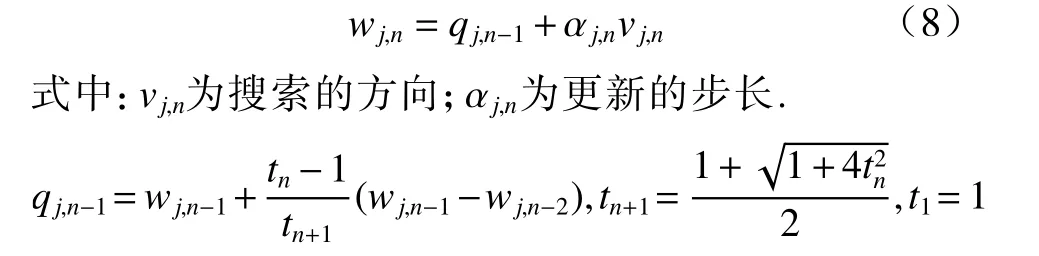
为了避免当代价函数曲线趋于收敛时出现上下抖动的现象，于是选择在迭代趋于收敛时改为利用常规共轭梯度法进行迭代优化.

综上所述，当发射天线数量为j，频率为k时，FCG-CSI 算法的步骤如下.

Step1: 输入散射场数据fj,k与入射场数据.

Step2: 初始化对比源wj,k,0与对比度χk,0.

ηS和ηD为权重因子，S表示测量区域，D表示目标区域，其表达式分别为

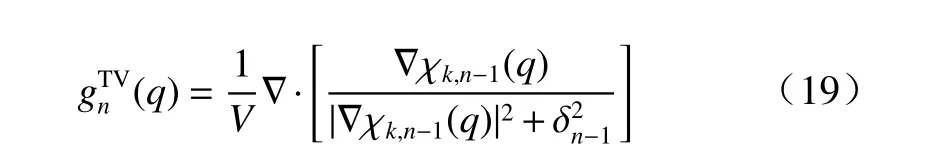
Step6: 当代价函数达到设定的误差值或迭代次数达到预设的最大迭代次数时，输出对比度矩阵χn并进行成像，算法结束，否则返回Step3.

3 仿真系统构建与成像实现

3.1 脑部模型建立与微波数据获取

运用多物理场仿真软件COMSOL 仿真人体脑部模型与发射天线，组成脑卒中微波检测成像系统的电磁散射正问题部分，进行微波数据的采集. 如图3所示，人脑模型采用均匀简易模型，即将脑部组织的相对介电常数统一为脑灰质和脑白质两种组织的相对介电常数的平均值，脑部的半径设为9 cm，内部血块的半径设为1 cm.

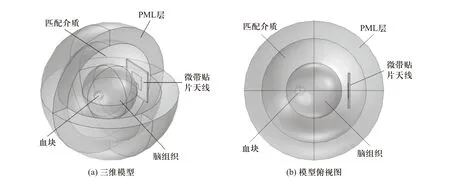
图3 微波脑部成像系统仿真模型Fig. 3 Simulation model of microwave brain imaging system

脑部各组织的电磁特性可通过DebyeⅡ 模型分析计算得到. DebyeⅡ 公式可表示为[19]

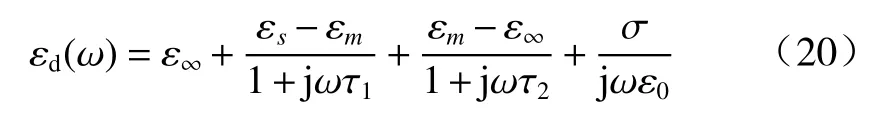
当入射微波信号的频率在1～4 GHz 变化时，人体脑部组织各项电磁模型参数如表1 所示，将各项参数代入DebyeⅡ模型公式中，可得到1～4 GHz 频率范围内脑组织与血块的平均相对介电常数与平均电导率. 最终经计算选取人脑均匀简易模型的相对介电常数为40，电导率选取为0.9 S/m；血块的相对介电常数选取为58，电导率选取为2.3 S/m.

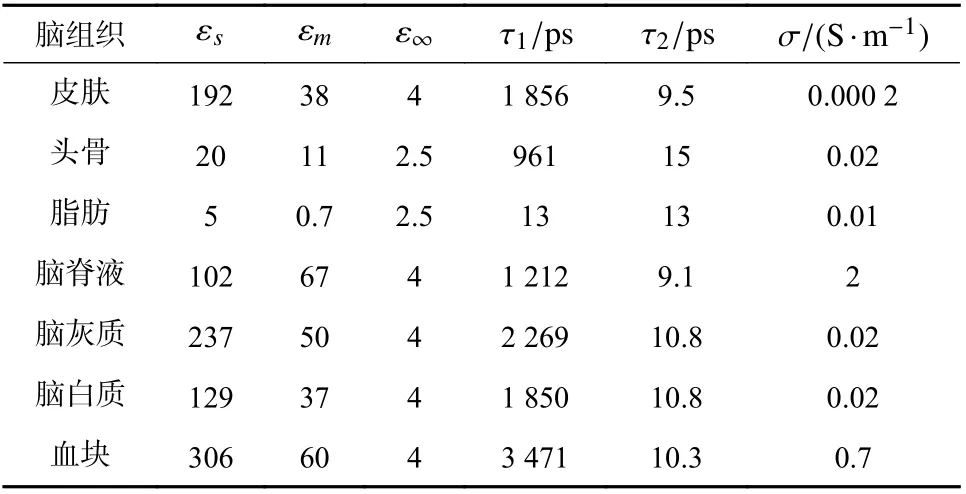
表1 脑部各组织Debye Ⅱ模型参数[19-21]Tab. 1 Debye Ⅱ model parameters of brain tissues

仿真系统模型的最外层设置完美匹配层（PML层），以确保散射体产生的散射场几乎完全被吸收，而不会有剩余部分反射到模型的外部边界上. PML层与人脑模型之间为匹配介质，匹配介质的介电常数应接近于脑部皮肤的介电常数，以减少天线和脑部之间的信号反射，从而确保电磁能量能够进入大脑内部，在这里选取匹配介质的相对介电常数为42，电导率选取为0.9 S/m.

发射天线采用微带贴片天线，其由一层薄金属、一个矩形FR4 介质块和一个接地面组成. 微带馈线、天线辐射器和接地面被建模为理想电导体表面，由50 Ω 的集总端口馈电来代表电源馈电. 由于从边缘向贴片天线馈电会导致输入阻抗非常高，进而导致不合需要的阻抗失配，因此本文中馈电方式选用嵌入式馈电，在贴片边缘与中心之间寻找一最佳馈电点，以改善50 Ω 馈电点与天线之间的匹配情况. 切口区域的宽度W选为尽可能大，既使得天线与微带之间的耦合最小又不会显著影响天线的特性，所选取的馈电线长度L使反射功率S11最小，其最佳尺寸可通过参数化扫描与优化得到. 经设计与优化最终得到天线结构与其S参数曲线如图4 所示，该天线的工作中心频率为2 GHz，可通过设计与更改贴片的尺寸大小来设计满足工作频率与天线增益要求的天线.

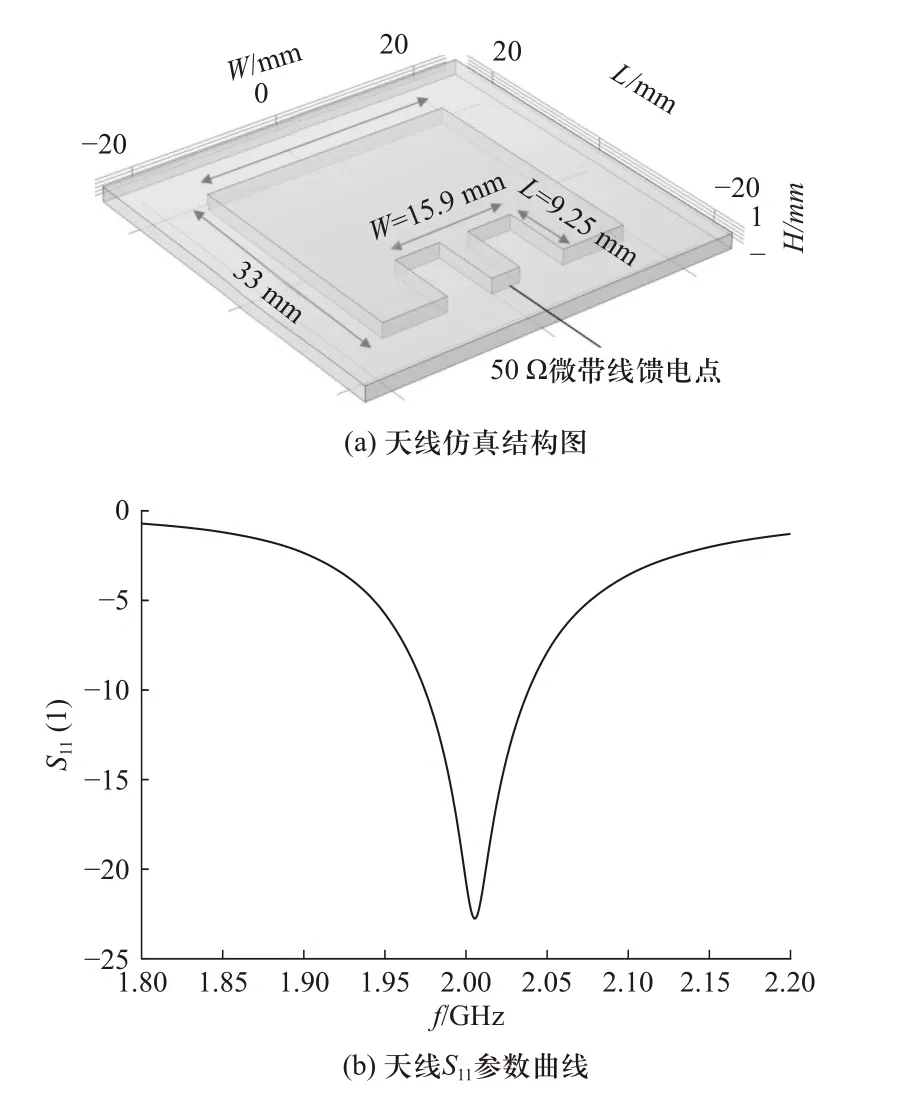
图4 天线示意图Fig. 4 Diagram of antenna

在距离脑部模型中心10 cm 的圆形轨道上均匀放置16 个收发天线，每两个天线的夹角为22.5°，如图5 所示收发天线按照逆时针的方向从1～16 依次编号. 在数据收集时，所有天线依次单独发射TM 波，COMSOL 软件将根据数据方程和状态方程，利用有限元法计算电磁场的时空分布，然后所有16 根天线进行微波数据的采集接收. 实验需要测得区域内存在散射体和不存在散射体两种情况下的电场值，存在散射体时测得的微波数据为总电场值，散射体不存在时得到的微波数据为背景电场值，最终获得21 616个微波数据，将这些数据导入MATLAB 中进行处理与反演成像.

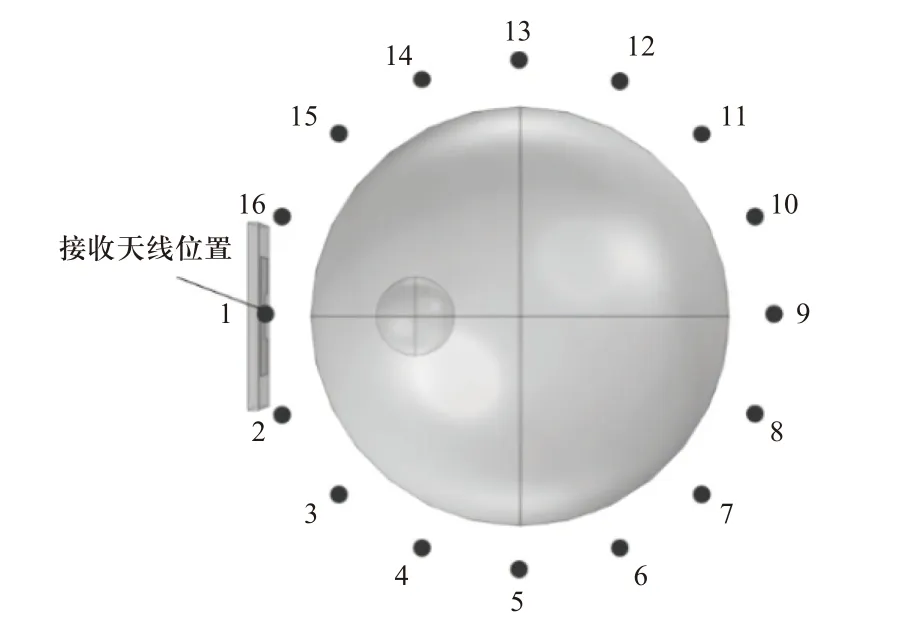
图5 收发天线分布Fig. 5 Distribution of transmit and receive antennas

3.2 成像结果与分析

脑卒中微波检测系统的数据处理端使用MATLAB 进行运算得到反演成像结果，将获得的微波数据导入MATLAB 中后，首先利用基于MATLAB 的FDFD 软件包“MaxwellFDFD”，根据每一个发射天线对应的16 个接收数据，计算得到该发射天线对应的整个区域的散射电场分布矩阵与背景电场分布矩阵，其中散射电场可根据公式Etot=Einc+Esct，由总电场与背景电场相减得到. 然后将散射场矩阵与背景电场（入射场）矩阵作为FCG-CSI 算法的输入进行反演成像.

为了量化成像算法的性能，利用 Δr指标来分析成像结果的位置误差，令Lreal为真实散射体的几何中心，Lmax为成像区域能量单元所在位置，S为目标散射体区域，Z为除去散射体区域外的成像区域，则用Δr来表示成像目标位置的精准度， Δr值越小，定位越准确. 位置误差 Δr定义为

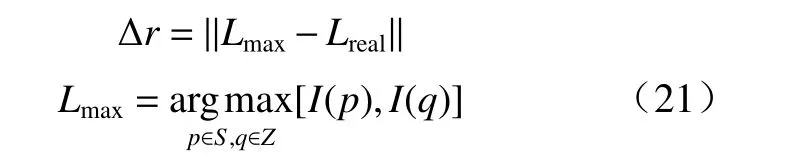
图6 成像结果Fig. 6 Imaging results

经计算得到分别在频率为2 GHz、2.38 GHz 时，通过CSI 算法与FCG-CSI 算法得到的成像结果中，预测血块的中心位置与实际模型中血块中心位置的偏差如表2 所示. 可以看出在两种频率下，FCG-CSI算法相对于常规CSI 算法的 Δr值均更小，成像结果更加精确.

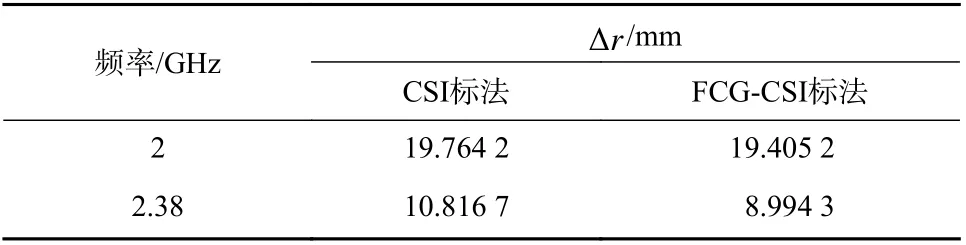
表2 成像结果位置误差Tab. 2 Position error of imaging results

图7 显示了随着迭代次数的增加，利用FCGCSI 算法和CSI 算法进行反演成像时目标函数的收敛曲线，可以看出在迭代初期，FCG-CSI 算法比CSI算法收敛速度更快. 目标函数反映的是通过迭代计算得到的“数据”与“目标”方程的值（即计算得到的散射场与总场的值）与实际测量的散射场与总场的值之间的误差，经过多次实验发现，当此误差值小于0.2 时基本可以完成准确成像，再往下迭代对成像结果的影响不大. 目标函数达到0.2 以下常规CSI 算法需要7 次迭代，而FCG-CSI 算法仅需要5 次迭代，因此FCG-CSI 算法的成像速度相比CSI 算法更快.

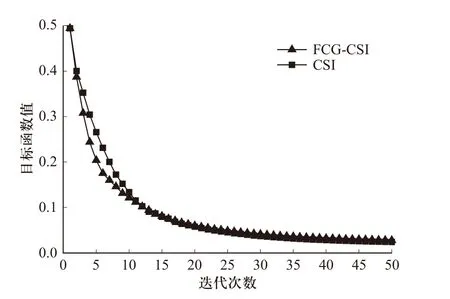
图7 迭代次数-代价函数曲线图Fig. 7 Curve of iterations number-cost function

为了进一步提高成像的精度，可以利用多个频率下得到的微波数据进行反演成像，其方法是在FCG-CSI 算法步骤的式(11)(13)(15)(17)(21)中·运算的基础上添加运算符，进行不同频率微波数据的叠加. 由于结合了多频微波数据信息，因此理论上可得到更精准的成像结果. 图8 显示了FCG-CSI算法在1.3 GHz、1.5 GHz、2 GHz、2.38 GHz 频率下，结合多频微波数据的反演成像结果. 此时的位置偏差值为Δr=5.385 2 mm. 可以看出此时的成像位置偏差均小于各单独频率下的成像结果，这说明利用多频率数据可以得到比单频率更精准的成像效果.

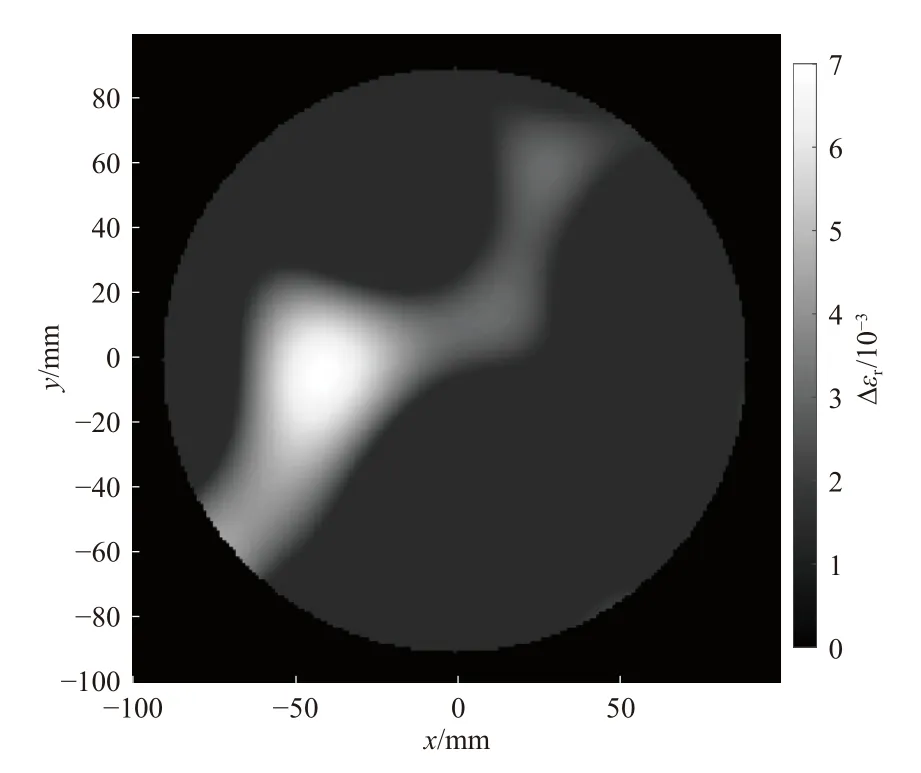
图8 多频数据FCG-CSI 算法成像结果Fig. 8 Imaging results of FCG-CSI algorithm for multi-frequency data

4 结束语

本文将对比源反演算法应用于出血性脑卒中的微波无损检测成像中，并在对比源反演算法的基础上加以改进，利用快速共轭梯度法来替代常规共轭梯度法来进行代价函数的优化，从而加速代价函数的收敛，提高反演成像的效率. 使用COMSOL 仿真软件进行脑部的建模与微波信号收发过程的仿真，然后将采集的微波数据导入MATLAB 软件中进行反演成像. 从成像结果来看，反演成像所使用的FCGCSI 算法相对于常规的CSI 算法，不仅收敛速度更快，成像结果也更加精确. 在利用多频数据进行FCGCSI 算法反演成像时，成像的位置误差可达到0.54 cm.

本文的研究均是在较为理想的仿真环境中完成，并未考虑实际测量环境中噪声的影响. 在后续研究中，将考虑到噪声对微波检测成像的影响并设法改善成像算法的抗噪声性能. 与此同时，在接下来的研究中也将进一步细化脑部模型，使仿真更加贴近于真实检测.