面向机械臂的永磁同步电机RBF 网络磁场矢量控制系统

唐晓刚，杨广雨，郇浩，余昊元，李可盈

（1. 航天工程大学 航天信息学院, 北京 101400；2. 北京理工大学 信息与电子学院, 北京 100081）

机械臂在工业、农业、国防和航天领域都有着广泛的应用. 以航天领域为例，其任务包括搭载视觉系统进行成像、转移航天员与航天装备、开展空间站建设维护等. 随着机械臂的应用场景多样化，对其性能需求变得更高. 作为机械臂的动力来源，开展伺服电机控制系统的研究对提高机械臂性能具有重要意义. 机械臂常用的电机种类为永磁同步电机（permanent magnet synchronous motor, PMSM），其反电动势波形为正弦型，转矩输出平稳[1]. 基于非完整约束的PMSM 模型是一个复杂非线性模型，具有很高的控制难度，其控制问题在电气工程领域受到广泛关注[2-4].

永磁同步电机有两种成熟的控制方法：磁场矢量控制法（field oriented control，FOC）和直接转矩控制法（direct torque control，DTC）. 文献[5]介绍了FOC算法，通过Clark 变换和Park 变换将电流信号解耦，得到了易于控制的线性分量，使用PI 控制器进行独立的控制，采用电压矢量脉宽调制策略获得逆变器的开关状态. FOC 算法具有很高的控制精度和能量利用率，缺点是动态响应慢、参数数量多而且整定困难[6]. TAKAHSSHI[7]介绍了DTC 算法，通过公式证明了在忽略电机相电阻的情况下，只需控制定子侧磁链大小和转矩角即可控制电机转矩，根据定子磁链角度通过查表的方法确定逆变器的开关状态. DTC算法结构简单并且具有很快的动态响应，缺点是位置控制精度低，转矩脉动较大[8].

随着微处理器计算能力的提高，国内外很多非线性控制方法取得了良好的效果[9]. ZHOU[10]使用了预测力矩控制法（predictive torque control，PTC），在DTC 算法的基础上将查表的部分改为代价函数，根据定子磁链估算值和转矩预测值确定当前的逆变器开关状态，但PTC 算法依然存在转矩脉动和控制精度低的缺点. LYU 等[11]使用了预测电流控制法（predictive current control，PCC），它是一种基于FOC 的优化算法，将调制器的部分用代价函数取代，根据电流在定子坐标系下的预测值来确定当前逆变器的开关状态，这种方法不需要使用调制器，因此控制概念更加简洁，但仍然存在转矩响应慢等问题[12].

1 被控对象建模

机械臂的关节由伺服电机连接构成，一种三自由度的机械臂模型如图1(a)所示. 机械臂的输出转矩与电机合成输出转矩相同，电机控制研究是机械臂设计的基础. 本文选择永磁同步电机作为被控对象，永磁同步电机的永磁体表面被设计成抛物线型，使其产生的气隙磁场呈正弦或准正弦分布[9]. 作为电动机使用时，通入正弦交流电能够驱动电机输出平稳的转矩. 一种三相二极、内定外转式的永磁同步电机结构如图1(b)所示

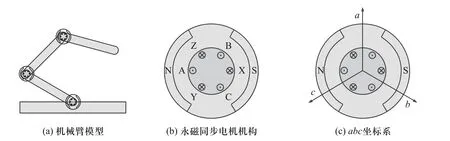
图1 机械臂与永磁同步电机结构Fig. 1 Robotic arm and PMSM structure

两侧的N，S 为永磁体在电机内侧的两个磁极，A，B，C定义为三相绕组的电流输入端，X，Y，Z 定义为三相绕组的电流输出端. 使用Y 型连接时，三个输出端在电机内部短接，以每相电流流入电机时该相绕组形成的磁场方向为正方向，建立如图1(c)所示的abc坐标系，abc坐标系是固定在定子上的静止坐标系.

在电机匀速转动时，abc坐标系下的三相电流采样信号Ia,Ib,Ic为相位相差120°的正弦波形，三相信号间具有很强的耦合关系，通过Clark 变换和Park 变换可以将信号解耦成两个线性电流分量[13]，变换的过程如图2 所示.

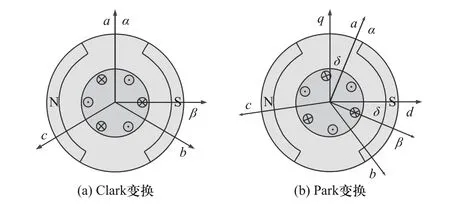
图2 两种坐标变换Fig. 2 Coordinate transformations

Clark 变换将Ia,Ib,Ic投影到 αβ坐标系， αβ坐标系是固定在定子上的静止直角坐标系，其 α轴与a轴重合，变换后的信号为两个相角相差90°电流分量Iα,Iβ，变换关系如下.

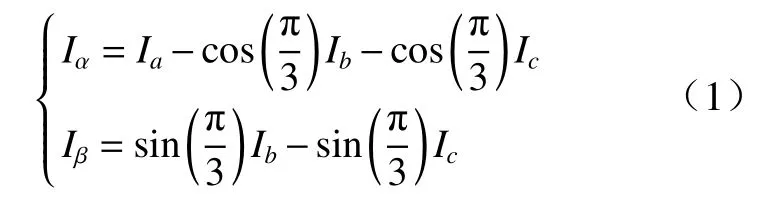
Park 变换将Iα,Iβ投影到dq坐标系，dq坐标系是固定在转子磁链上的旋转直角坐标系，为了获取磁链角 δ，需要获取转子的实时位置信息，变换后的信号为两个线性电流分量Id,Iq变化关系如下.

在dq坐标系下，永磁体为表面凸出式结构的永磁同步电机转矩方程[9]为

式中，p为电机极对数， Ψ0为永磁体所产生的定子每相主磁链，其大小不可调节，因此只要控制电流交轴分量Iq的大小，即可实现转矩的快速控制.

2 磁场矢量控制系统

磁场矢量控制是一种结合了Clark 变换、Park 变换、PI 控制器和矢量脉宽调制器于一体的永磁同步电机控制方案，具有能量利用率高和控制精度高的优点，非常适合用于机械臂的高精度伺服控制. 一种使用电机编码器的磁场矢量控制系统结构如图3 所示.

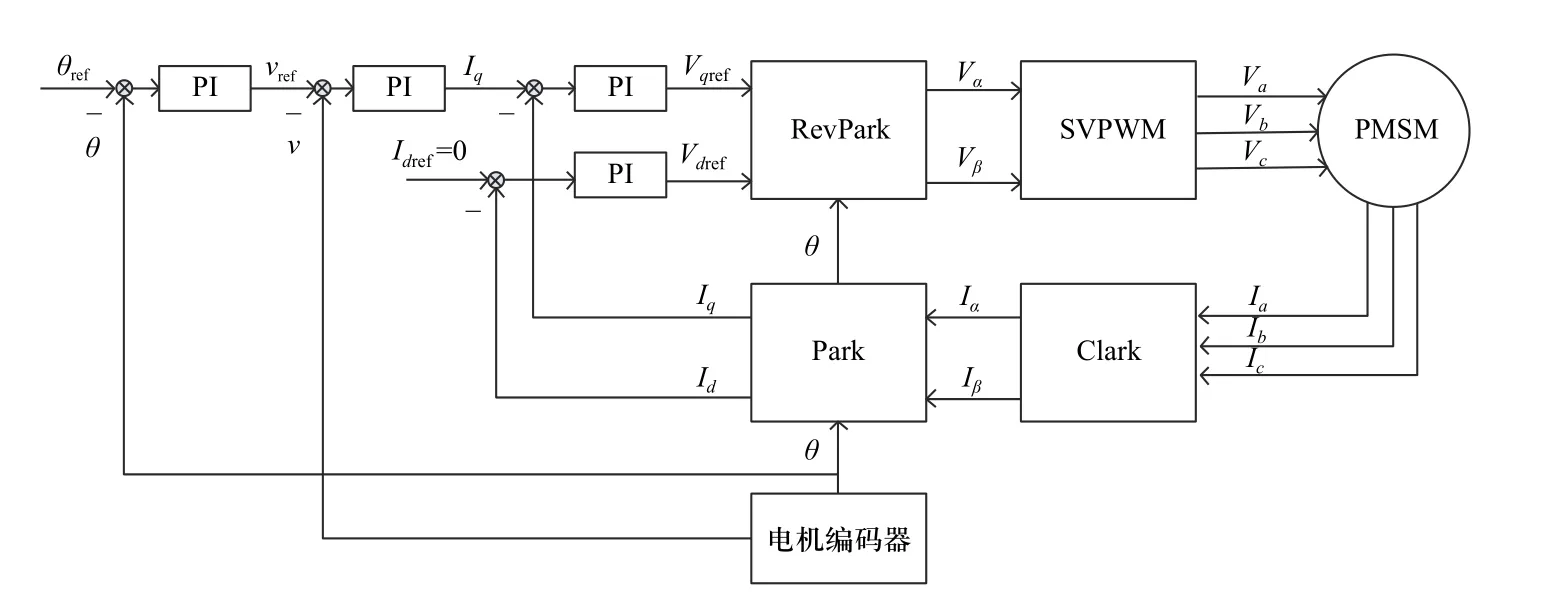
图3 磁场矢量控制系统结构Fig. 3 Field oriented control system structure

图中，编码器获取转子的位置 θ，并估算出转子的速度v= θ˙. 采样电流经过解耦得到电流分量Id和Iq.用PI 控制器消除不做功的直轴电流分量Id，降低能量损耗；用级联结构的PI 控制器进行位置、速度和电流Iq的闭环控制，控制电机轴切向的作用力，从而控制电机输出转矩.

FOC 算法使用了4 个PI 控制器，PI 控制器存在参数整定的问题，导致控制系统的环境适应能力较差；积分项的滞后作用导致控制器的动态响应不足；较多的控制器参数可能使调参工作变得十分困难，但FOC 算法的解耦思想是高精度控制中必不可少的.

3 RBF 网络磁场矢量控制系统设计

为了解决FOC 算法参数整定和动态响应不足的问题，本文在FOC 算法解耦和调制的基础上，重新设计了控制器结构，基于模型辨识的思想，用RBF 网络建立了控制器的正向传播模型. RBF 网络具有结构简单、辨识精度高、收敛速度快的特点，这非常符合电机控制器的需要. 为了保证RBF 网络的收敛和参数的自适应调整，引入了监督学习和在线学习的机制.

3.1 RBF 网络监督控制

RBF 网络是一种前馈型神经网络，它将输入变量映射到高维空间，反映输入与输出之间的正向传播关系，网络能够以任意精度逼近非线性模型[10]. 一种多输入单输出的RBF 网络的结构如图4(a)所示.

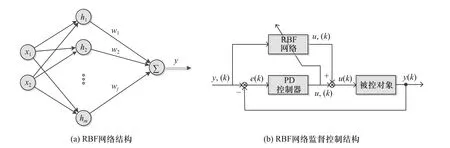
图4 RBF 网络及其监督控制器结构Fig. 4 RBF network and its supervisory controller structure

网络由输入层、隐含层和输出层组成，输入层通过高斯径向基函数映射到隐含层.

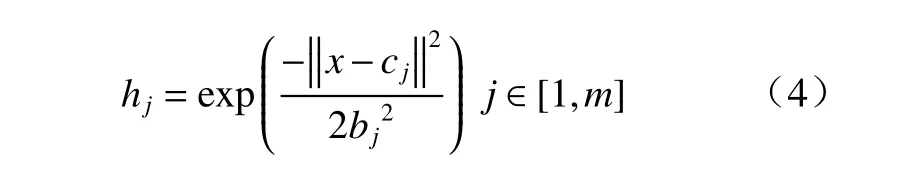
RBF 网络监督控制的结构如图4(b)所示. RBF网络用和PD 控制器共同输出，PD 控制器提供稳定的控制率辅助在线训练，网络更新的误差指标为

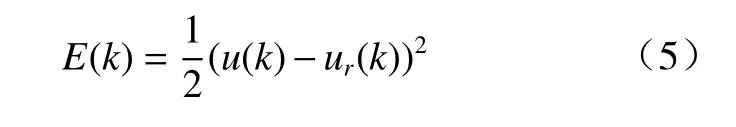
采用梯度下降法在线学习，更新公式为

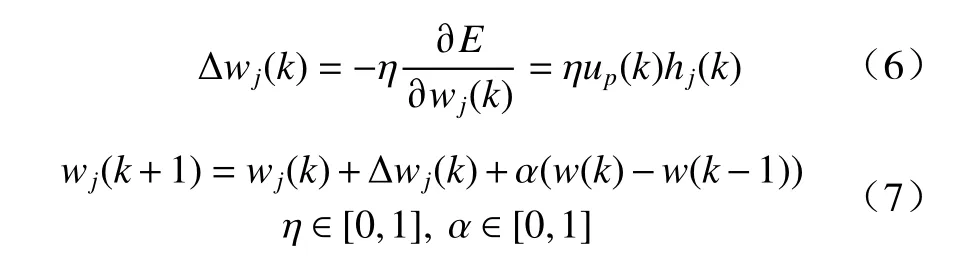
式中： η为学习率； α为动量项用于加快收敛速度.

在初始阶段，PD 控制器占主导地位，RBF 网络进行权重更新，当网络参数收敛后，PD 控制器的输出趋近于0，此时控制系统达到稳定状态. 当环境发生变化时，只要输入还在网络的映射范围内，RBF 网络都能自动修正权重以适应新的状态，相比于PI 控制器而言，监督控制的结构在面临环境动态变化时具有更强的鲁棒性.

3.2 RBF 网络磁场矢量控制器

RBF 网络要求输入量的取值范围必须连续，且网络的输入维度不能太高，单个网络的算法时间复杂度为O(Cn).C为每个维度下的神经元的个数，n为网络维度. 根据FOC 反馈回路的状态矩阵S=[θ,v,Id,Iq]和期望信号，设计RBF 网络磁场矢量控制器的结构如图5 所示.

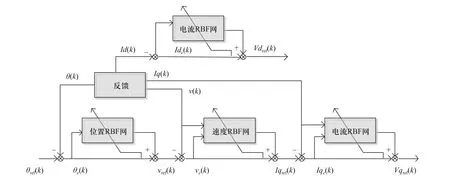
图5 RBF 网络磁场矢量控制器Fig. 5 RBF network field oriented controller

RBF-FOC 控制器保持了三环级联的控制结构，这样既可以减少每个网络的输入维度，又保证了算法可以自由运行位置、速度、电流控制模式. 控制器共使用了4 个RBF 网络监督控制单元，并简化了PD控制器的结构. 考虑到电机的位置范围无法约束且处处相同，位置环输入仅设位置误差θe(k)；考虑到直轴电流环的期望为0，即Ide(k)=-Id(k)，直轴电流环输入仅设电流误差Ide(k)；速度环和交轴电流环均设置两个输入，分别为当前状态与当前误差. 控制器的整体输出为电压在dq坐标系下的期望矩阵Vref=[Vdref,Vqref]，与FOC 算法的控制器输出相同. 控制器输出在经过RevPark 变换和矢量脉宽调制后，产生三相逆变电路的驱动信号最终作用于被控电机，此时控制系统进入下一控制周期.

RBF 网络监督控制器消除了PI 控制器的积分单元，某一时刻下的输出仅取决于网络参数，在网络收敛且参数合理的情况下，理论上具有比PI 控制器更快的响应速度.

3.3 控制系统稳定性分析

为了验证系统的稳定性，以电机位置环为例，取Lyapunov 函数L：

当L的差分为负时，可以证明位置误差会逐渐趋近于0.

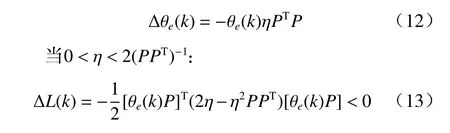
此时位置误差趋近于0，同理可以证明其他控制环误差趋近于0，控制系统具有渐进稳定性.

4 仿真实验

针对机械臂的性能需求，本文设计了3 组对比实验验证FOC 算法和RBF-FOC 算法在快速转矩、稳定输出和环境干扰情况下的性能表现，设置稳定时间(s)、超调量、上升时间(s)等性能指标. 实验平台的实物图如图6 所示.实验的硬件组成如表1 所示.参考实验电机的运行参数，设计RBF 网络参数的输入范围和分辨率如表2 所示.

图6 实验平台Fig. 6 Experiment platform

表1 硬件组成Tab. 1 Hardware composition

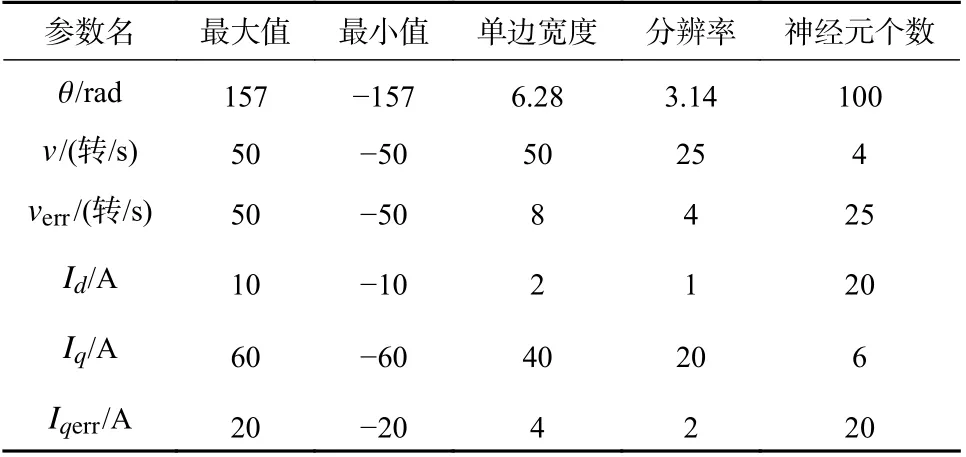
表2 RBF 网络参数Tab. 2 RBFNN parameters

两种算法中使用的控制器参数如表3 所示.

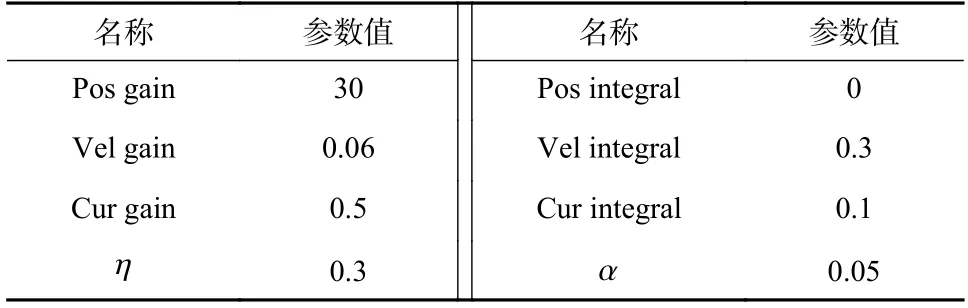
表3 控制器参数Tab. 3 Controller parameters

从以上参数可以看出，FOC 算法需要使用6 个控制器参数，RBF-FOC 控制器需要使用两个控制器参数和一组网络参数，其中网络参数的确定基于电机运行参数和处理器计算规模，实际需要调参的只有两个控制器参数，RBF-FOC 算法的调参的难度相对更低.

4.1 快速转矩实验

机械臂主要运行在位置控制模式下，快速平稳的到达预期位置是其核心需求. 实验1 对比了两种算法在空载和负载情况（66 g 飞轮负载）下期望位置突变时的性能表现. 实验设计如下：初始状态时位置期望θref=0 rad，0.4 s 后θref=4π rad. 实验结果如图7所示.

图7 快速转矩实验对比结果Fig. 7 Quick torque experiment comparison results

如图7 所示，空载时RBF-FOC 算法的稳定时间为0.1 s，最高转速为50 转/s，FOC 算法的稳定时间为0.7 s，最高转速为9 转/s，两者均无静差；负载情况下两种算法的稳定时间和最高转速均有所下降，对比结果基本相同. 从实验结果可以看出，空载和负载情况下，RBF-FOC 算法都具有更快的动态响应.

4.2 稳定输出实验

电机在高转速下的动态性能反映了控制系统运行的稳定性，实验2 对比了两种算法在空载和负载情况（66 g 飞轮负载）下期望速度突变时的性能表现.实验设计如下：初始状态时速度期望vref=20，0.4 s 后vref=40，单位为转/s. 实验结果如图8 所示.

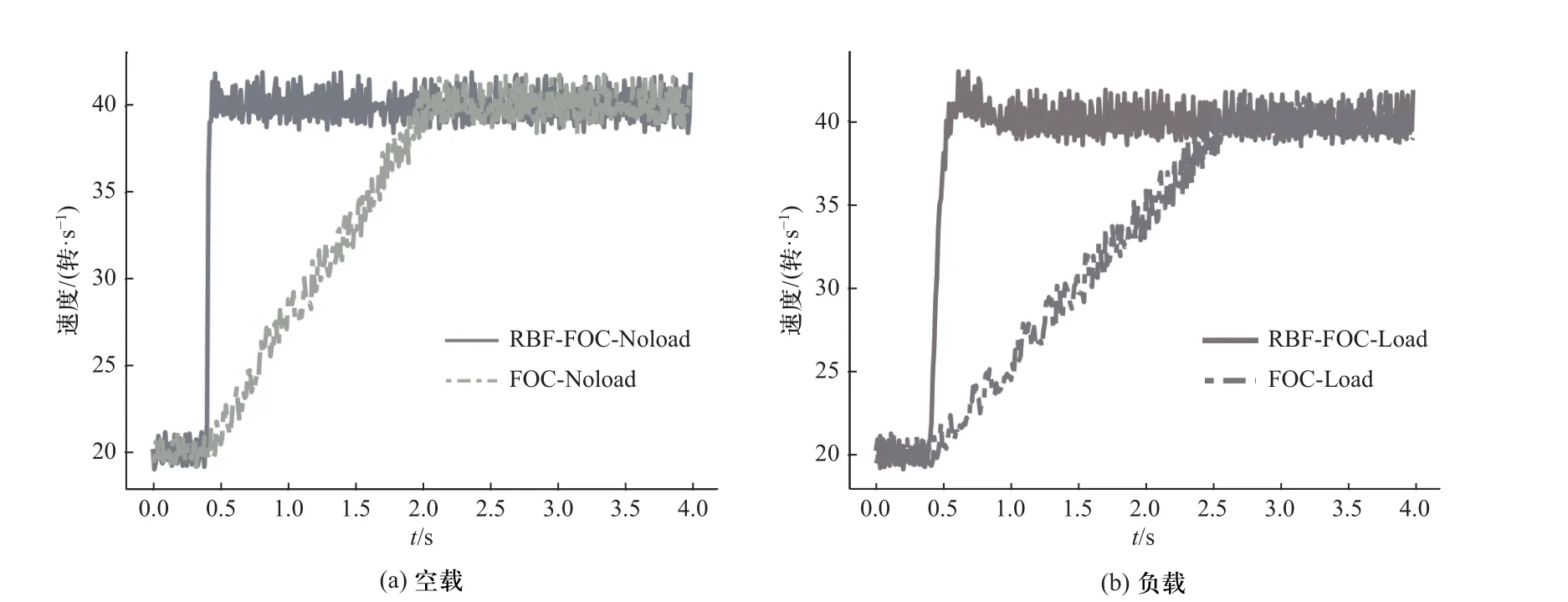
图8 稳定输出实验对比结果Fig. 8 Stable output experiment comparison results

如图8 所示，两种控制算法都可以达到期望速度，并具有良好的稳态性能. RBF-FOC 算法得益于快速的动态响应，空载情况下的上升时间为0.05 s，FOC 算法为1.4 s；负载情况下RBF-FOC 算法的上升时间为0.2 s，FOC 算法为2.3 s. 实验证明RBF-FOC算法在速度突变时具有良好的稳定性，并具有更快的动态响应能力. 图中的振荡现象主要源自编码器速度估算的误差.

4.3 环境干扰试验

机械臂在运行过程中可能会遇到外部的干扰，这要求控制器具有足够的稳定裕度来保证系统的鲁棒性. 实验3 设计如下：将两种控制器运行在位置保持模式，1.2 s 后对转子长时间施加相同的扰动力矩，对比了两种算法的性能表现. 实验结果如图9所示.

如图9(a)所示，FOC 算法的上升时间为0.4 s，稳定时间为1.8 s；RBF-FOC 算法的上升时间和稳定时间均为0.3 s. 受到外界扰动后RBF-FOC 算法的稳定时间和响应速度都明显优于FOC 算法. FOC 算法出现扰动后位置环产生了73%的超调，RBF-FOC 算法无明显超调；原因在于RBF 网络监督控制器具有在线学习的优势，转矩扰动产生后，网络参数进行了自适应更新. 从实验结果可以看出，RBF 网络监督控制器具有更强的抗扰动能力.

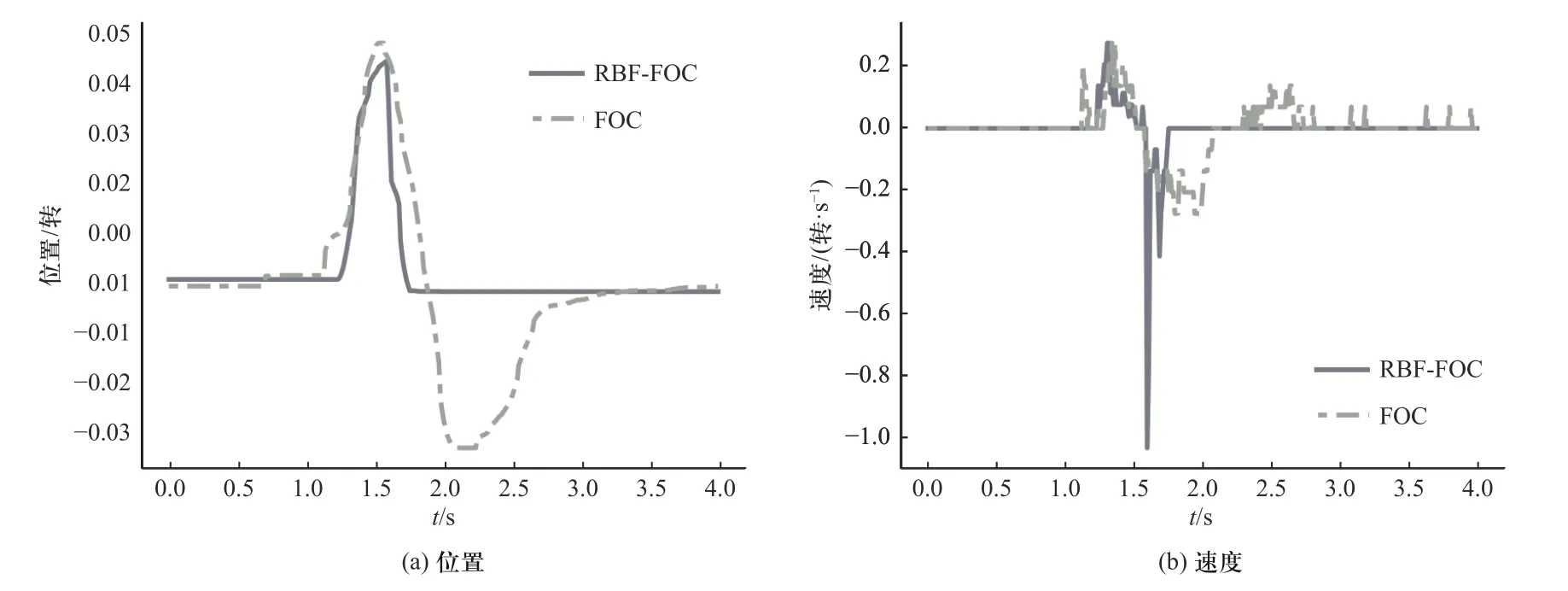
图9 环境干扰试验对比结果Fig. 9 Environmental interference experiment comparison results

5 结 论

机械臂的电机伺服控制系统的研究对提高机械臂性能具有重要意义，本文选择永磁同步电机作为研究对象，提出了一种RBF 网络磁场矢量控制系统，改善了级联PI 控制器的积分项迟滞作用，解决了FOC 算法动态响应慢的问题；RBF 网络构成的控制器建立了被控对象的正向传播模型，减少了需要人工设定的参数量；监督学习的方法确保了控制系统的全局渐进稳定性；在线学习的机制使控制系统在面临动态环境变化时具有自适应能力. 实验证明，RBF-FOC 系统相比FOC 系统在动态响应速度和抗扰动能力上都有了显著的提升，并具有良好的运行稳定性. 算法的改进对电机伺服控制系统设计具有一定参考意义，下一步将会对无传感器位置检测、电压矢量脉宽调制以及采样电流滤波等内容进行更深入的研究，进一步优化控制系统结构.