爆炸成型弹丸垂直穿透钢板靶后破片飞散特性

邢柏阳，赵建霞，陈亮，胡爱虔，朱福林，刘建禄，郭锐，侯云辉

（1. 四川航天系统工程研究所, 四川, 成都 610100；2. 南京理工大学 机械工程学院, 江苏, 南京 210094；3. 西安现代控制技术研究所, 陕西, 西安 710065）

EFP 作为摧毁装甲目标的一种典型毁伤元，穿透目标防护结构后，能够在内部形成大量破片，进而对人员、设备等造成严重毁伤. 但是，目前依靠图像识别的方法很难判断目标内部的破片分布情况，进而难以估计其受损状况，在打击窗口稍纵即逝的作战条件下，极可能由于未能一次性达到作战目的而暴露我方的打击意图，使敌方有充足时间组织大规模反攻，因此，有必要获得一种利用EFP 打击目标前的初始条件并对目标内部破片分布进行量化预测的方法.

杨祥等[1]采用Autodyn 的光滑粒子动力学（smoothed particle hydrodynamics，SPH）方法对战斗部爆炸驱动破片加速过程进行了数值模拟，结果与实验值基本吻合. 王海福等[2]采用Autodyn 的SPH 方法对遭遇速度为1.5～2.5 km/s 下圆柱钨弹丸垂直碰撞装甲靶板产生的二次破片云分布特征进行了数值模拟，建立了二次破片云质量及空间分布预测模型，结果表明，数值模拟和模型预测均与实验结果相吻合.WEN 等[3]和邸德宁等[4]运用Autodyn软件中的SPH方法，数值模拟了球撞击薄板所形成的靶后破片云，将数值仿真结果与PIEKUTOWSKI[5]的实验结果进行对比分析后发现两者相吻合，表明Autodyn 软件中SPH 方法是可信的. DALZELL等[6]使用Autodyn 数值仿真EFP 正侵彻靶板时发现，SPH 方法比欧拉(Euler)方法和拉格朗日(Lagrange)方法更具优势，并且，运用SPH 方法模拟EFP 穿透厚度较厚靶板比穿透较薄靶板的计算精度更高. 叶严等[7-8]采用有限元仿真软件Autodyn-3D 中的SPH 方法对EFP 正侵彻钢靶形成靶后破片的过程进行了数值仿真，与靶场实验结果进行对比表明：仿真的EFP 成型参数、靶后破片空间分布状态和靶板开孔特征均与实验较为吻合. 黄炫宁等[9]基于量纲分析及正交设计理论，利用Autodyn 软件中SPH 算法研究了EFP 成型参数、弹和靶材料参数对靶后破片云形状的影响，建立了EFP 垂直侵彻靶后破片云形状的数学描述模型. 王昕等[10]为研究EFP 穿透钢靶后的后效威力，设计了EFP 对45 号钢靶板的侵彻实验，采用X 光摄影方法观测了EFP 穿透靶板后的破片云形态及飞散特性，通过测量靶板后一定距离处后效板上的穿孔，得到了靶板后破片数量. WANG 等[11]采用了X 光摄影与后效靶结合的实验手段，并在LS-DYNA软件中运用FEM-SPH 方法建立了EFP 侵彻靶板形成靶后破片云的过程模型，数值仿真所得的靶后破片云形状、靶后破片数量分别与X 光摄影、后效靶穿孔数量相吻合.

但是，目前分析靶后破片在各飞散角内的数量的文献较少，因此本文将分析EFP 贯穿靶板后各飞散角内靶后破片的数量与初始条件的关系，为武器平台的使用者、装甲车辆的设计者提供参考依据.

1 数值仿真方法验证

在文献[10 - 12]的实验中，EFP 战斗部的装药直径为56 mm，药型罩为壁厚3 mm 的球缺形罩，装药为长径比0.86 的压装JH-2，壳体厚度为2.52 mm.EFP 正侵彻厚度为20 mm 的45 号钢板，靶板和EFP的粒子直径均为0.5 mm，45 号钢和高导无氧铜的状态方程均假设为Gruneisen，拉伸屈服应力均通过Johnson-Cook 模型表达，材料参数取自文献[10-12]. 实验中测得EFP 着靶速度为2 120 m/s，45 号钢板的长、宽均为200 mm，数值仿真模型中的参数设置与实验保持一致，并对靶板边界施加固定约束，由于是垂直穿透，建立1/4 模型，仿真模型如图1(a)所示. 数值仿真中EFP 沿中心轴线对称的1/2视图如图1(b)上半部分所示，文献[10 - 12]实验中EFP 沿中心轴线对称的1/2 视图如图1(b)下半部分所示，EFP 前端部位的半径为6.4 mm，EFP 长度为41.5 mm.

图1 数值仿真模型Fig. 1 Numerical simulation model

EFP 在0 时刻着靶，80 μs 和95 μs 时刻数值仿真的靶后破片云如图2(a)和2(b)上半部分所示，文献[10 - 11]实验的X 光照片如图2(a)和2(b)下半部分所示.

由图2 可以发现，80 μs 和95 μs 时刻下，数值仿真的靶后破片云长轴与文献[10 - 11]实验的靶后破片云长轴之比均为1，短轴之比分别为1.11、1.05，表明了数值仿真结果是可靠的. EFP 在0 时刻着靶，95 μs时刻数值仿真与文献[10]实验的靶后破片云径向及头部的膨胀速度对比如表1 所示.

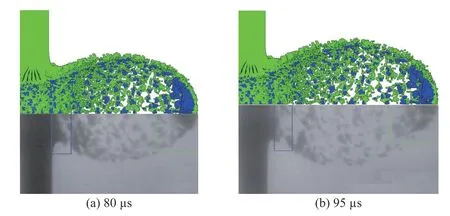
图2 靶后破片云对比Fig. 2 The comparison of behind-armor debris clouds

由表1 可以发现，95 μs 时刻数值仿真的靶后破片云径向及头部的膨胀速度与文献[10]的实验结果偏差分别为1.1 %和0.7 %，表明了数值仿真结果是可靠的. 综上所述，本文所采用的数值仿真方法是可靠的.

表1 靶后破片云的膨胀速度对比Tab. 1 The comparison of expansion velocity of the BAD

2 靶后破片飞散特性

采用Autodyn-3D 软件中的SPH 方法，建立某EFP 垂直穿透靶板的数值仿真模型，靶板材料选择装甲钢，状态方程假设为线性，参数取自文献[13]；EFP 材料选择铜，状态方程假设为Gruneisen，参数取自文献[14]（详见文后附录），均质装甲钢和铜的拉伸屈服应力采用Johnson-Cook 模型表达. 某EFP 最大长度为98.0 mm，尾部最大半径为28.5 mm，尾部空腔形状假设为圆锥体，底面半径为23.36 mm，高为36.24 mm，EFP 粒子直径取为0.5 mm，EFP 在三维条件下的1/2 模型如图3所示.

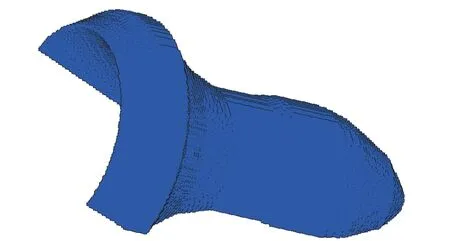
图3 某EFP 在三维条件下的1/2 模型Fig. 3 The 1/2 model of a EFP in three-dimension condition

为提升计算效率，靶板形状设为圆柱体，由于是正侵彻，故建立1/4 模型，在靶板边界施加3 处固定约束，分别为圆柱体圆周边缘的中点和2 个端点，宽度均为5 mm. 靶板半径为EFP 最大半径的5 倍，即142.5 mm，采用渐变尺寸粒子，靶板圆心至半径为114 mm 处的粒子直径为0.5 mm，半径为114 mm 处至半径为142.5 mm 处的粒子直径为0.7 mm. 圆柱体的高度即为靶板厚度，记为H0，定义H0re=H0/D，其中H0re为相对靶板厚度，D为EFP 战斗部的装药直径，D=125 mm；EFP 以v0着靶速度垂直穿透靶板，定义v0re=v0/vint，其中v0re为EFP 相对着靶速度，vint为EFP成型时刻的速度，vint=1 950 m/s. EFP 在0 时刻着靶，0.5 ms 时刻的靶后破片速度很高且基本稳定，故选取此时刻条件下的靶后破片云作为研究对象，在实际情况中，靶后破片与最终毁伤的目标间距离仅为几米，靶后破片的速度衰减可以忽略，故假设此时刻后的靶后破片均做匀速直线运动. 利用Autodyn 软件自带的破片信息识别读取功能（material location→output fragment analysis）可以获取所有破片的质量、空间位置、X/Y/Z方向的动量等信息.

定义飞散角φ=2arctan (Rφ/hφ)，其中，hφ表示靶板背面与后效靶前面的距离，并假定hφ=1 350 mm，Rφ表示破片在后效靶上的落点与后效靶圆心的距离，如图4 所示.

Waters Acquity UPLC-TQ-D型液质联用仪(美国，Waters公司)，H1650R台式高速冷冻离心机(中国，上海卢湘仪离心机仪器有限公司)，BT125D电子天平(德国，赛多利斯股份公司)，G560E涡旋混合器(美国，Scientific Industries公司)。

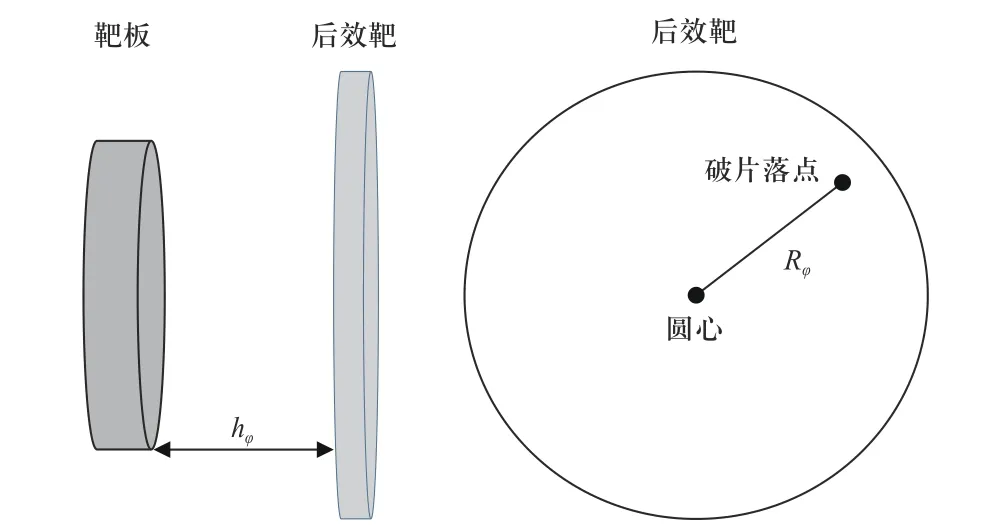
图4 飞散角φ 的定义Fig. 4 The definition of spatial emission angle φ

Nrei(φ)表示飞散角小于φ的靶板或EFP 产生的靶后破片相对累计数量，其定义为

式中：Ni(φ)为靶板或EFP 产生的飞散角小于φ的靶后破片数量；Ni为靶板或EFP 产生的靶后破片总数量.

采用式（2）拟合靶板和EFP 产生的靶后破片相对累计数量与飞散角的关系，ai、bi均为待定系数.

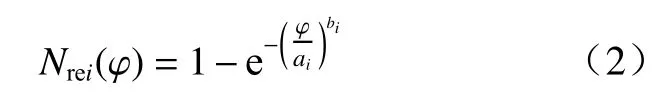
以“H0re= 0.480 0，v0re= 0.871 8”工况为例，靶后破片相对累计数量和飞散角的关系如图5 所示.

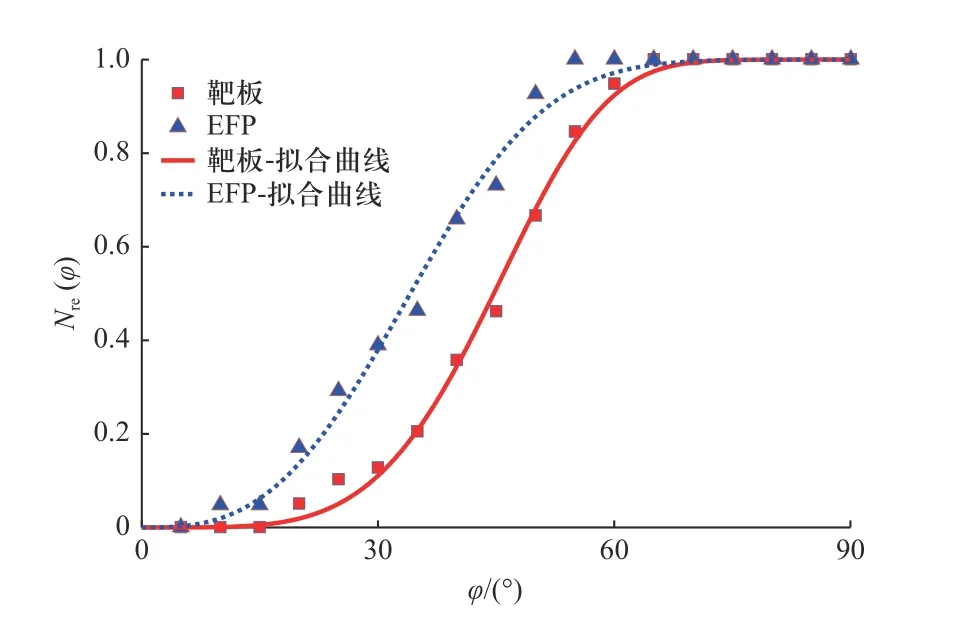
图5 相对累计数量和飞散角的关系Fig. 5 The relationship between the relative accumulative number and the spatial emission angle

在图5 中，靶板和EFP 产生的靶后破片相对累计数量与飞散角的关系及Weibull 累积分布函数曲线的确定系数分别为1.00 和0.99. 在表2 中列出25种工况下的待定系数取值及对应的确定系数.

由表2 可以发现，对于某EFP 以5 种相对着靶速度（0.871 8，0.897 4，0.923 1，0.948 7，0.974 4）垂直穿透5 种相对靶板厚度（0.240 0，0.320 0，0.400 0，0.480 0，0.560 0）的靶板（25 种工况）而言，以Weibull 累积分布函数拟合靶板和EFP 产生的靶后破片相对累计数量与飞散角的关系，确定系数最小为0.96，最大为1.00，表明了采用式（2）拟合靶板和EFP 产生的靶后破片相对累计数量与飞散角的关系是可行的.

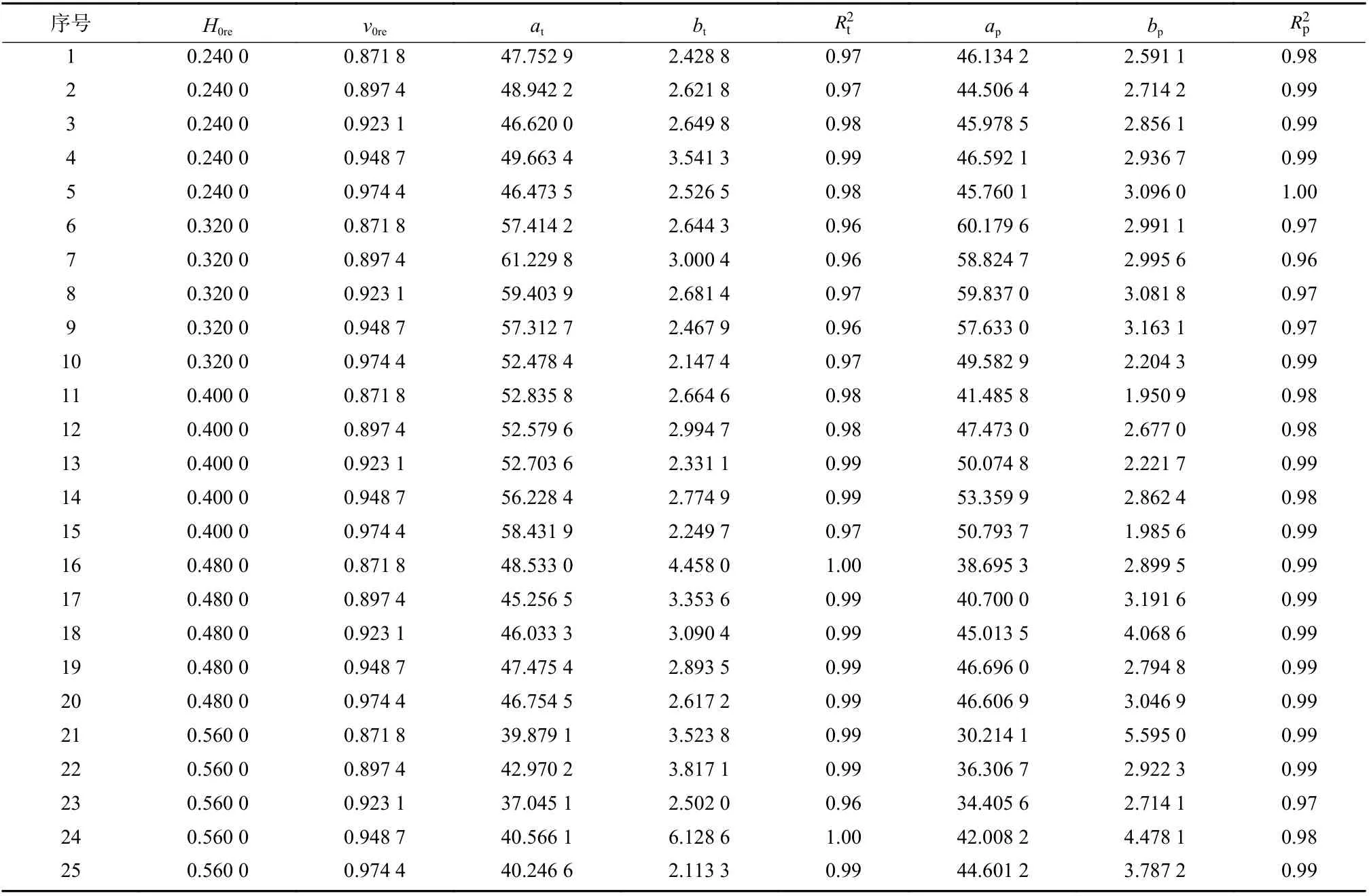
表2 待定系数取值及对应的确定系数Tab. 2 The values of undetermined coefficients and the determination coefficients

计算H0re相同、v0re不同时at（ap、bt、bp）的标准差Sat（Sap、Sbt、Sbp）如表3 所示.

表3 H0re 相同、v0re 不同时at（ap、bt、bp）的标准差Tab. 3 The comparison of the standard deviation of at(ap、bt、bp)as H0re is same and v0re is different

计算v0re相同、H0re不同时at（ap、bt、bp）的标准差Sat（Sap、Sbt、Sbp）如表4 所示.

对比分析表3 和表4 可以发现，v0re相同、H0re不同时at（ap、bt、bp）的标准差有15 个（共20 个），大于H0re相同、v0re不同时at（ap、bt、bp）的标准差，表明当H0re相同、v0re不同时at（ap、bt、bp）的变化幅度相对较小，以相同H0re、不同v0re下at（ap、bt、bp）的平均值作为该H0re条件下所对应的at（ap、bt、bp）值是可靠的，故以相同H0re、不同v0re下at（ap、bt、bp）的平均值作为目标函数，H0re作为自变量，拟合方程的确定系数列于表5.

表4 v0re 相同、H0re 不同时at（ap、bt、bp）的标准差Tab. 4 The comparison of the standard deviation of at(ap、bt、bp)as v0re is same and H0re is different

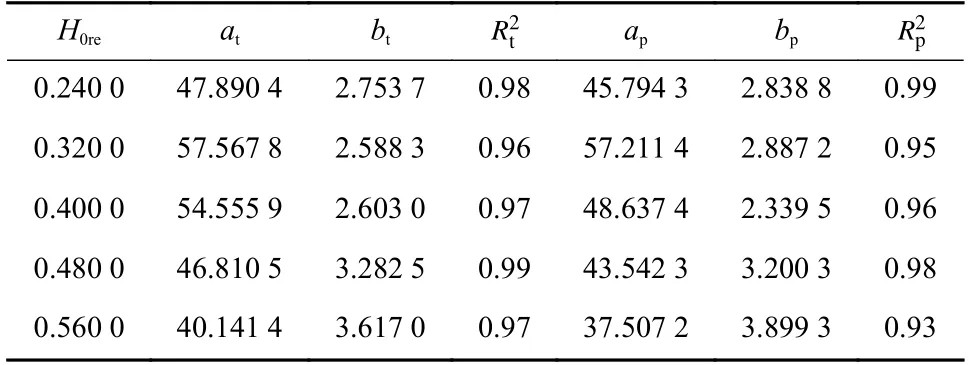
表5 at（ap、bt、bp）的平均值及拟合方程的确定系数Tab. 5 The mean value of at（ap、bt、bp） and determination coefficients

由表5 可以发现，确定系数最小为0.93，最大为0.99，表明以相同H0re、不同v0re条件下的at（ap、bt、bp）平均值作为拟合方程系数是可行的. 因此，在0.871 8≤v0re≤0.974 4 时，以H0re为自变量，以相同H0re、不同v0re条件下的at（ap、bt、bp）平均值为因变量，进行拟合可以得到式（3）～（6）.

3 定量关系验证

由于实验中很难在区分破片来源（靶板和EFP）的条件下准确统计各飞散角内的靶后破片数量，因此，有必要利用数值仿真的方法检验靶后破片的数量与所处飞散角定量关系的准确性. EFP 着靶前的初始条件为H0re= 0.440 0，v0re= 0.910 3，靶后破片相对累计数量和飞散角的关系如图6 所示.

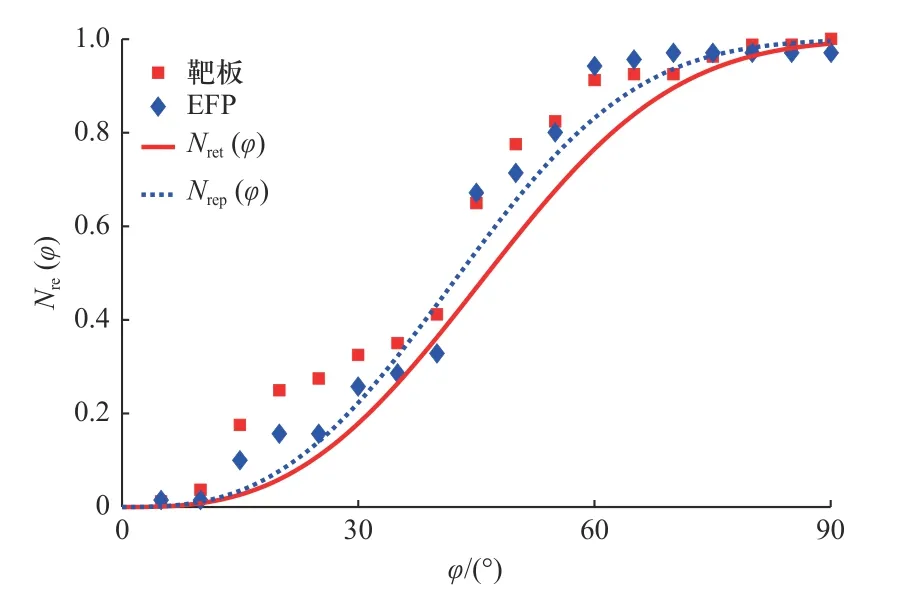
图6 相对累计数量和飞散角的关系Fig. 6 The relationship between the relative accumulative number and the spatial emission angle

图6 中，靶板和EFP 对应点分别表示来源为靶板和EFP 的数值仿真数据，Nret(φ)由式（2）（3）（4）得到，确定系数分别为0.89；Nrep(φ)由式（2）（5）（6）得到，确定系数分别为0.98. 这表明了本文所提出的靶板和EFP 产生的靶后破片相对累计数量和飞散角的关系是可靠的.

4 结 论

利用Autodyn 软件数值仿真研究了EFP 垂直穿透靶板所形成的靶后破片的飞散特性，得到了以下2 点结论：

① 当着靶速度介于1 700 ～ 1900 m/s，靶板厚度介于30 ～ 70 mm 时，靶后破片相对累计数量和飞散角的关系主要是由靶板厚度决定的，受着靶速度、破片来源的影响比较小，并且靶后破片相对累计数量随飞散角的增加而呈Weibull 累积分布函数式增加；

② 利用本文所提出的靶后破片相对累计数量与飞散角的关系，可以通过靶板厚度、着靶速度、破片来源量化预测装甲目标内部的破片分布情况，武器平台的指挥管控者可以据此分析判断打击目标的何部位能够造成内部最佳的毁伤效果，装甲车辆的设计制造者可以据此安排制定人员设备在何位置能够减少外部打击的毁伤损失.

（责任编辑：匡梅）

附录

线性状态方程为

式中： ρ0为参考密度；K为材料体积模量.

Gruneisen 状态方程为

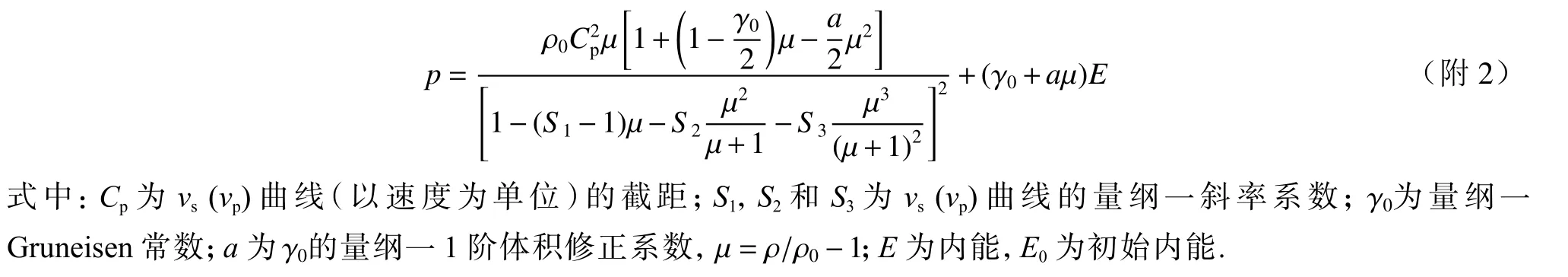
Johnson-Cook 模型表达式为

式中：S为拉伸屈服应力； ε为等效塑性应变；ε˙*= ε˙/ε˙0为量纲一等效塑性应变率，ε˙0一般取1 s-1；T*=(T-Tref)/(Tmelt-Tref)，其中Tref为参考温度（一般取室温），Tmelt为常态下材料的熔化温度；A、B、C、n和m为材料常数.45 号钢和高导无氧铜的材料参数如表S1 和表S2 所示.

表S1 45 号钢参数[10-12]Tab. S1 Parameters of No. 45 steel[10-12]

表S2 高导无氧铜参数[10-12]Tab. S2 Parameters of high-conducting oxygen-free copper[10-12]

均质装甲钢和铜的材料参数如表S3 和表S4 所示.

表S3 均质装甲钢参数[13]Tab. S3 Parameters of rolled homogeneous armor[13]

表S4 铜参数[14]Tab. S4 Parameters of copper[14]