小题大做 别有洞天*——以一道中考选择压轴题为例

李加禄

(云南省昆明市第三中学,650500)

本文对2021年浙江省嘉兴市一道中考试题进行深入探究，在引导学生进行知识关联和方法系统构建的同时，挖掘试题的潜在育人价值，帮助学生掌握基础知识，提升解题能力，开阔解题视野.

一、原题呈现

如图1,在∆ABC中,∠BAC=90°,AB=AC=5,点D在AC上,且AD=2,点E是AB上的动点,连结DE,点F,G分别是BC和DE的中点,连结AG,FG,当AG=FG时,线段DE长为( )

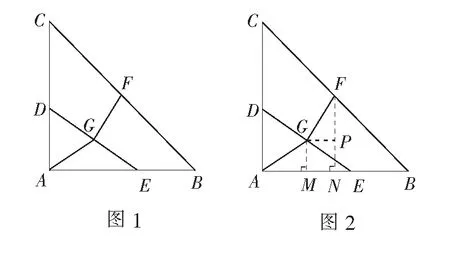
二、总体分析

本题以等腰直角三角形为背景,以线段中点为载体,融入动态几何问题,题干简单,图形简洁,以小见大,凸显素养.仔细研读题目条件,不难发现,我们只要求出AE的长,即可根据勾股定理求出DE的长,或者根据题目隐藏条件AG=DG=EG=FG,求出这四条中的任何一条线段即可.因此,如何运用好中点相关知识,联想“中点”的生长点:等腰三角形遇中点,三线合一;直角三角形遇中点,斜中线定理;中点遇中点,三角形中位线定理和倍长中线等是破题的关键.

三、解法探究

1.曲径通幽——化斜为直,构造方程

评析当遇到“斜线段”时,如本题中的AG,FG,我们可通过“斜线段”的两个端点作水平线和铅垂线,构造直角三角形,将其“化斜为直”,再利用勾股定理及中位线定理分别表示出线段AG和FG的长,最后运用等量关系构造方程求解.

2抽丝剥茧——利用对角互补,构造全等

评析考虑到在∆DEF中,FG=DG=EG,易证∠DFE=90°,进而得四边形AEFD对角互补.又AF平分∠DAE,进而联想通过“截长补短”或“旋转变换”构造全等三角形解决“对角互补模型”问题,此时真有一览众山小之感.

3.上屋搭梯——遇角平分线作两边垂线,构造全等

评析根据等腰三角形遇中点,联想到三线合一,可得AF平分∠CAB,进而尝试遇角平分线作角两边垂线,构造全等三角形,然后利用全等三角形的性质实现线段的转化和迁移,最后巧设未知数构造方程使问题得解.此种解法由“中点”搭台,“角平分线”唱戏,“全等”压轴,精彩纷呈.

4.欲擒故纵——遇直角,构造“K”型相似

评析当题中出现特殊角是直角时,我们通常作两条垂线构造“一线三直角”全等或相似,这是处理直角问题的重要策略.如解法4中,证得∠DFE=90°,进而联想构造“K”型相似.

5. 柳暗花明——“圆”来如此,构造辅助圆

评析若能根据题目条件的本质特征觅得解题思路,可使问题化难为易,化繁为简,化隐为显.如题中隐含了GA=GD=GE=GF或四边形AEFD对角互补,可联想到构造辅助圆,则问题变得“圆”来如此简单.

6. 另辟蹊径——以“数”解“形”,建立坐标系

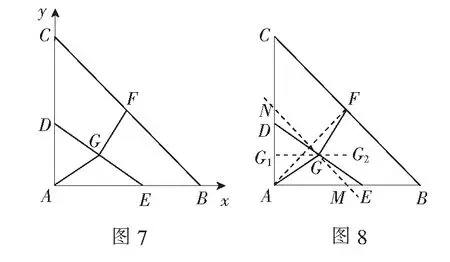
评析若题中存在垂直关系,如本题中AB⊥AC,则可建立平面直角坐标系,将几何问题代数化,图形性质坐标化,通过数形结合,使解题思路更加直观简洁.

7.豁然开朗——主从联动,利用“瓜豆原理”

评析不难发现,题目中有两个动点,点G随着点E的运动而运动,则由“瓜豆原理”,可知从动点G和主动点E的轨迹类型相同,都为线段,进而确定点G的轨迹为∆DAE的中位线G1G2,再运用几何图形的性质求解.此种解法利用极端化思想确定动点的轨迹,化动为静,真可谓无限风光在险峰.

四、解题反思

基于以上对一个中点动态问题的深入探究,我们从不同的视角出发,通过联想、变通和构造不同的模型,进行多角度的转化,挖掘其隐藏条件,衍生出不同的求解思路.而破解题目的关键就是洞悉中点的“生长点”和构造几何模型.如本题中构造直角三角形列方程、构造“K”相似模型、构造对角互补模型、构造辅助圆、构建直角坐标系等促进知识间的关联和重构,但无论哪一种解法都需要学生对基本图形的结构有深刻的认识.一题多解不仅丰富了解题思路,同时也使一些基本知识和基本方法得到充分展示,提升了学生的类比能力和迁移能力,达到“以题会类”的归一境界,从而培养学生思维的发散性、广阔性、灵活性和深刻性.