基于宇称时间对称的电场耦合式无线电能传输系统
张良权,丘东元,谢帆
(华南理工大学 电力学院,广东 广州 510641)
无线电能传输(wireless power transfer,WPT)系统由于安全可靠、使用方便、无接触火花等优势,已在消费电子、家用电器、电动汽车和植入式医疗等领域中得到广泛的研究[1-4]。其中,电场耦合式无线电能传输(electric-field coupled wireless power transfer, ECPT)系统主要利用电场实现电能的无线传输,具有电磁干扰小、穿透金属能力强、无涡流损耗等优点[5],适用于电动汽车的无线充电[6-7]。目前,恒定的输出功率是ECPT系统的重要研究内容之一。然而,随着发射极板和接收极板之间的传输距离发生变化,ECPT系统的传输特性也随之改变,限制了该技术的应用[8-9]。为了补偿负载电路、耦合机构以及补偿网络的参数变化,文献[10]将工作频率调谐到谐振频率,并调整了发射侧和接收侧电路的匹配网络,但系统需要多个回路控制器。文献[11]提出利用可变电抗的整流器来补偿WPT系统中耦合极板变化的方法,该整流器能不断补偿耦合极板之间的错位和距离变化,但其拓扑结构较为复杂。
宇称时间(parity time, PT)对称性的概念源于量子力学[12],是指量子系统在宇称变换和时间反演变换下的对称性。其中P-反转指空间反演,T-反转指时间反转。在WPT系统中,P变换时应将两侧电路拓扑结构作对称。经过变换后,WPT系统中的原边电路的拓扑与副边电路拓扑互换位置;而T变换时,使得虚数单位j反转为-j,时间t反转为-t。为了满足PT对称的条件,WPT系统需要在变换前后系统性质不发生改变。从实际物理意义的角度来说,系统原副边电路拓扑相同,且电源提供的能量增益与系统内阻及负载损耗的能量相同。文献[13]中在WPT系统中首次引入PT对称的概念,使用运算放大器构造非线性饱和增益元件,实现了输出功率和传输效率在一定传输距离范围内保持恒定,解决了传输距离变化对系统传输特性的影响。尽管系统的输出功率仅有19.7 mW,但这激发了学者们对PT对称原理在WPT系统中的研究与应用。文献[14]中利用半桥逆变器构造出提供非线性增益饱和元件的负电阻,该方式整体提高了系统的输出功率和传输效率。文献[15]在PT对称WPT系统中使用非线性开关放大器,相较于文献[13]进一步提高了传输效率,在65 cm的传输距离内所设计系统的输出功率大约为10 W,传输效率几乎恒定为92%。文献[16]通过应用PT对称原理改进了无人机飞行无线动态充电平台,所设计的WPT平台对处于一定空间内的无人机能保持稳定的输出功率,传输效率约为93.6%。文献[17]将PT对称原理应用到单线ECPT系统中,所提出的系统能在大约34 m的传输距离内保持恒定的输出功率,且传输效率为60%;但其两侧的球形电容通过单根导线相连,没有实现真正的无线电能传输。文献[18]将PT对称原理应用于双耦合(电场耦合和磁场耦合)WPT系统中,在1.4 m的距离内保持恒定70 W的输出功率和77%的传输效率。然而,上述研究主要集中在磁耦合式WPT系统中[13-22],在ECPT系统中应用PT对称理论的相关研究成果仍然较少。
在实际的应用场景中,传统ECPT系统的极板耦合情况或传输距离通常是不确定的或不固定的,而ECPT系统的输出功率和传输效率对耦合极板间距离的变化很敏感[8-9]。为了解决ECPT系统在传输距离增加时输出功率急剧下降的问题,本文提出一种基于PT对称的ECPT系统,所提系统能在金属极板耦合情况发生变化时仍能实现稳定高效的功率传输。系统利用电力电子变换器构造出负电阻以满足所需的PT对称条件,分析比较PP型和SS型2种补偿拓扑的ECPT系统的频率特性、传输特性以及适用场合,并对所提系统进行仿真验证。
本文由4个部分组成:第1章介绍ECPT系统结构以及耦合机构的广义耦合模型和等效Π模型;第2章对2种补偿拓扑的ECPT系统分别进行建模与分析,通过电路理论推导出2种系统的工作频率、输出功率和传输效率的表达式,并比较了2种系统的频率特性、传输特性以及适用场合;第3章分别对2种拓扑结构下的ECPT系统的恒功率恒效率特性进行仿真验证;第4章给出结论。
1 ECPT系统模型
ECPT系统的结构如图1所示。ECPT系统一般由直流电源、高频逆变电路、补偿网络、耦合极板、整流电路和负载组成,主要分为能量发射部分和能量接收部分,发射侧和接收侧之间通过金属极板相互耦合。系统的直流电源经过高频逆变后作用在金属极板上,使得发射极板与接收极板间形成交互电场。在交互电场作用下极板间产生位移电流流过极板,实现极板间的能量传输。接收侧接收到发射侧的能量后,再经过整流滤波得到符合要求的直流电提供给用电设备。

图1 ECPT系统结构
系统两侧电路的固有谐振频率f1和f2、金属极板之间的距离和负载RL等因素均会对其输出功率和传输效率产生影响。在ECPT系统中,两侧的补偿网络能减小极板电容的无功功率,提高系统的传输功率[5]。
常见的耦合极板结构如图2所示。其中图2(a)和图2(b)分别为一对平行极板和垂直极板的耦合模型。上述极板结构中考虑了多个金属极板(P1—P4)之间存在的交叉耦合情况,可等效为与耦合电感模型相似的广义电容耦合模型[23],如图2(c)所示。其中C1和C2分别为发射侧极板和接收侧极板的自电容,CM为发射侧极板和接收侧极板之间的互电容,表达式为[24]:
(1)
(2)
式中ω为角频率。
图2(d)为耦合极板的等效Π模型。该模型可解耦发射侧和接收侧电路,以便应用基本电路定律对ECPT系统进行分析。同时,由式(2)可求得等效Π模型的电路方程为:

图2 耦合极板的等效模型
(3)
2 系统电路分析
为了验证PT对称原理在ECPT系统中的可行性,分别对PP型和SS型2种补偿拓扑的ECPT系统进行建模,推导并分析系统相应的频率特性和传输特性。
2.1 PP型补偿结构
基于PT对称的PP型ECPT系统结构如图3所示,图3中:Udc为直流电压;Idc为直流电流;L为大电感;Q1、Q2、Q3和Q4均为逆变侧开关管;R1和R2分别为两侧电路的固有损耗;L1和L2分别为两侧电路补偿电感;Ro为整流侧的负载电阻;RL为等效负载损耗;VD1、VD2、VD3和VD4均为整流侧二极管;Cf为滤波电容;uin、u1、u2和uR分别为逆变桥输出电压、发射侧极板两端电压、接收侧极板两端电压以及等效负载两端电压;i1和i2分别为发射侧电路电流和接收侧电路电流。

图3 基于PT对称的PP型ECPT系统结构
由于电容两端电压不能突变的特点,为了避免输入电压矩形波直接加在耦合极板上,通过将电压源Udc串联一个大电感L等效为系统的输入电流源。为了构造提供非线性饱和增益的负电阻,系统利用逆变器输出电压振荡过零点产生门极信号驱动相应开关管,使得逆变器输出的电流与电压始终保持同相位。同时,电能在接收侧电路经过整流和滤波后,提供给负载Ro。此时发射侧电路的输入电流
i1=sgn(uin)Idc.
(4)
式中:uin为逆变桥的输出电压;Idc为逆变桥直流侧电流;sgn(·)为符号函数,满足
(5)
基于PT对称的PP型ECPT系统的等效电路图如图4所示。其中,发射侧电路中的负电阻-R0向电路提供系统增益,耦合极板采用等效Π模型。
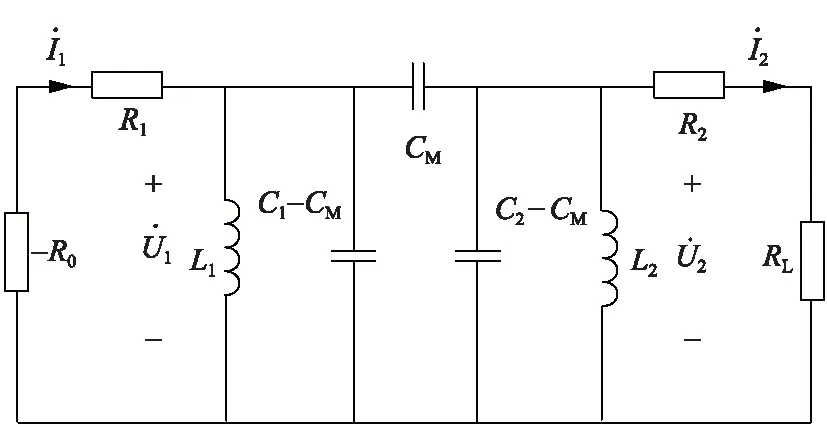
图4 基于PT对称的PP型ECPT系统等效电路
对图4电路应用基尔霍夫电压定律进行分析,其电路方程为
(6)
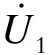
可将式(6)改写为:
(7)
为满足PT对称,电路发射侧的固有谐振频率和接收侧的固有频率应相同,即ω0=ω1=ω2。因此式(7)可简化为
(8)
式中:g1=1/(R1-R0),g2=1/(R2+RL)。
要使得所述系统方程存在非零解,其行列式应为0,即有
(9)
式(9)为基于PT对称的PP型ECPT系统需要满足的PT对称条件。将该条件的实部和虚部分开计算,可得:
(10)
(11)
对于上述条件,下面将分为2种情况(ω≠ω0和ω=ω0)讨论。
a)当系统工作角频率不同于系统固有谐振角频率时,即ω≠ω0。由式(10)可求得系统负电阻的值
(12)
可以看出,系统负电阻的值与发射侧电路极板电容及电路损耗电阻、接收侧极板电容及电路损耗电阻、负载电阻有关。由式(11)可求得此时系统工作角频率
(13)

式(13)表明方程有2个角频率解,系统出现频率分岔现象。要使系统的工作角频率为实数,须满足条件
(14)
也即
(15)
满足上述条件下,系统的增益与损耗相等,认为其处于PT对称态。式(15)可进一步简化为
(16)
式中kc为系统的临界耦合系数。
由式(16)可知,临界耦合系数与系统固有谐振角频率、接收侧极板电容及电路损耗、负载电阻成反比;也即对于同一耦合极板,系统固有谐振角频率或负载电阻越大,临界耦合系数越小,两侧的耦合极板能在更大的变化范围内使系统处于PT对称态。
b)当系统工作于固有谐振频率时,即ω=ω0。此时由式(11)求得此时系统的负电阻
(17)
由式(17)可知,当系统工作于固有谐振频率时,负电阻不仅与发射侧电路极板电容及电路损耗、接收侧极板电容及电路损耗、负载电阻有关,而且受到耦合系数的影响。此条件下,系统的增益不再与损耗相等,认为系统处于破碎的PT对称态或PT破碎态。
由式(16)可以看出,耦合系数可以分为2部分:k≤kc和k>kc。从物理意义来看,这2个部分分别对应于PT对称区域和破碎的PT对称区域[13]。结合上述讨论结果可知:当k>kc时,系统出现频率分岔现象,工作角频率不再保持为恒定值;当k≤kc时,系统则工作在固有谐振角频率ω0。
进一步,由上面的分析可以推导出所提系统的电压增益特性和传输特性。将不同工作状态下的负电阻条件式(12)和式(17)分别代入系统的电路方程式(8),可以求得系统的电压增益
(18)
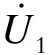
根据欧姆定律,系统电压、电流的关系满足
(19)
根据等效电路(图4),PP型ECPT系统的输出功率和传输效率分别为:
(20)
(21)
式中:I1为发射侧电流i1的有效值;I2为接收侧电流i2的有效值。
将式(18)、(19)代入式(20),可以求得基于PT对称的PP型ECPT系统的输出功率
(22)
同样地,将式(18)、(19)代入式(21),可以求得基于PT对称的PP型ECPT系统的传输效率
(23)
由式(22)、(23)可以看出:①当k>kc时,所提系统的输出功率仅与发射侧极板电容、接收侧极板电容、输入电流和负载电阻有关,与耦合系数无关;同时系统的传输效率仅与发射侧固有损耗和极板电容、接收侧固有损耗和极板电容、负载电阻有关;即使系统的耦合系数k发生变化,所提系统仍能保持恒定的输出功率和传输效率。②当耦合系数k≤kc时,式(22)、(23)中系统的输出功率和传输效率不仅与上述①中因素有关,而且与系统固有角频率和耦合系数有关;当耦合系数k发生变化时,系统的输出功率和传输效率不再保持在恒定值。
2.2 SS型补偿结构
相比于PP型ECPT系统拓扑结构,SS型ECPT系统在补偿电路上采用串联电感的方式。由于系统的补偿电感和极板电容串联,流过电感的电流不能突变,SS型ECPT系统的直流输入为电压源而非电流源。控制回路通过逆变器输出电流振荡过零点产生门极信号驱动相应开关管,使得逆变器输出的电压与电流始终保持同相位,从而构造出提供增益的负电阻。其系统结构如图5所示,其中uc1和uc2分别为发射侧极板自电容两端电压和接收侧极板自电容两端电压。
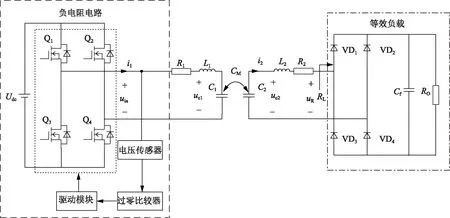
图5 基于PT对称的SS型ECPT系统结构
同样地,发射侧电路的输入电压
uin=sgn(i1)Udc.
(24)
SS型补偿拓扑的ECPT系统等效电路如图6所示,其中耦合极板同样采用等效Π模型。
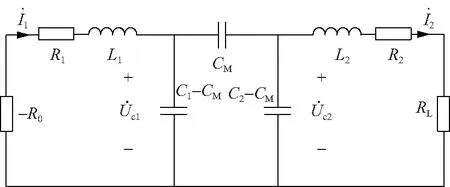
图6 基于PT对称的SS型ECPT系统等效电路
2种补偿拓扑的系统电路分析方法基本相同。首先应用基尔霍夫定律进行电路分析,得到系统的基本电路方程
(25)
同时,耦合极板的电路方程为
(26)
结合式(25)和(26)可得
(27)
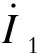
由两侧电路固有谐振角频率相等,即ω1=ω2=ω0,同时在ECPT系统中CM≪C1、C2,即k2≪1,为简单起见,式(27)中将(1-k2)项近似为1,式(27)可简化为矩阵形式:
(28)
对比式(8)和式(28)可知,2种拓扑结构的ECPT系统在电路方程上有相似之处。为了使得方程有非零解,上述矩阵方程的行列式也应等于0。即有
(29)
式(29)即为基于系统负电阻的SS型ECPT系统需要满足的PT对称条件。对该条件的分析过程与2.1节基本相同,此处简化其推导过程,直接给出基于PT对称的SS型ECPT系统传输特性对应的表达式。
基于PT对称的SS型ECPT系统处于PT对称态的关键条件为
k>kc=ω0C2(R2+RL).
(30)
对比式(16)、(30)可知,SS型ECPT系统与PP型ECPT系统的临界耦合系数互为倒数,SS型ECPT系统的临界耦合系数与固有谐振角频率、接收侧极板电容和电路损耗以及负载电阻成正比。也即对于同一耦合极板,当系统固有谐振角频率或负载电阻越小时,临界耦合系数越小,系统处于对称态时两侧的耦合极板有更大的变化范围。
由式(29)求得SS型ECPT系统的工作角频率
(31)

由式(13)、(31)可以看出,2种补偿拓扑结构的ECPT系统频率特性基本相同。耦合系数可分为2个区间:k≤kc和k>kc,分别对应于PT对称区域和破碎的PT对称区域。结合上述讨论结果可知:当k>kc时,系统出现频率分岔现象,工作角频率不再保持为恒定值;当k≤kc时,系统则工作在固有谐振角频率ω0。
同样地,SS型ECPT系统相应的负电阻
(32)
分析式(32)可知:在PT对称区域,SS型ECPT系统的负电阻仅与发射侧电路极板电容及电路损耗、接收侧极板电容及电路损耗、负载电阻有关,这与PP型ECPT系统的负电阻条件一致。当系统处于破碎的PT对称态时,负电阻不仅与谐振角频率、发射侧电路极板电容及电路损耗、接收侧极板电容及电路损耗、负载电阻有关,而且受到耦合系数的影响。
将负电阻条件式(32)代入式(28)可以求得基于PT对称的SS型ECPT系统的电流增益
(33)
相似地,由系统等效电路图6可知SS型ECPT系统的输出功率和传输效率的表达式分别与式(20)和式(21)相同。
将式(32)、(33)代入式(20)可以得到基于PT对称的SS型ECPT系统的输出功率Po关于输入电压U1的表达式为
(34)
式中QR为考虑等效负载的品质因数,QR=1/[ω0C2(R2+RL)]。
同时,将式(33)代入式(21)可以得到基于PT对称的SS型ECPT系统的传输效率
(35)
分析式(34)和式(35)可知:当数k>kc时,基于PT对称的SS型ECPT系统的输出功率和传输效率均与耦合系数无关;当k≤kc时,系统的输出功率和传输效率将随耦合系数的变化而变化。
2.3 系统特性比较
由上述分析可知,SS型和PP型的ECPT系统的传输特性非常相似。2种拓扑结构的系统特性对比总结见表1。
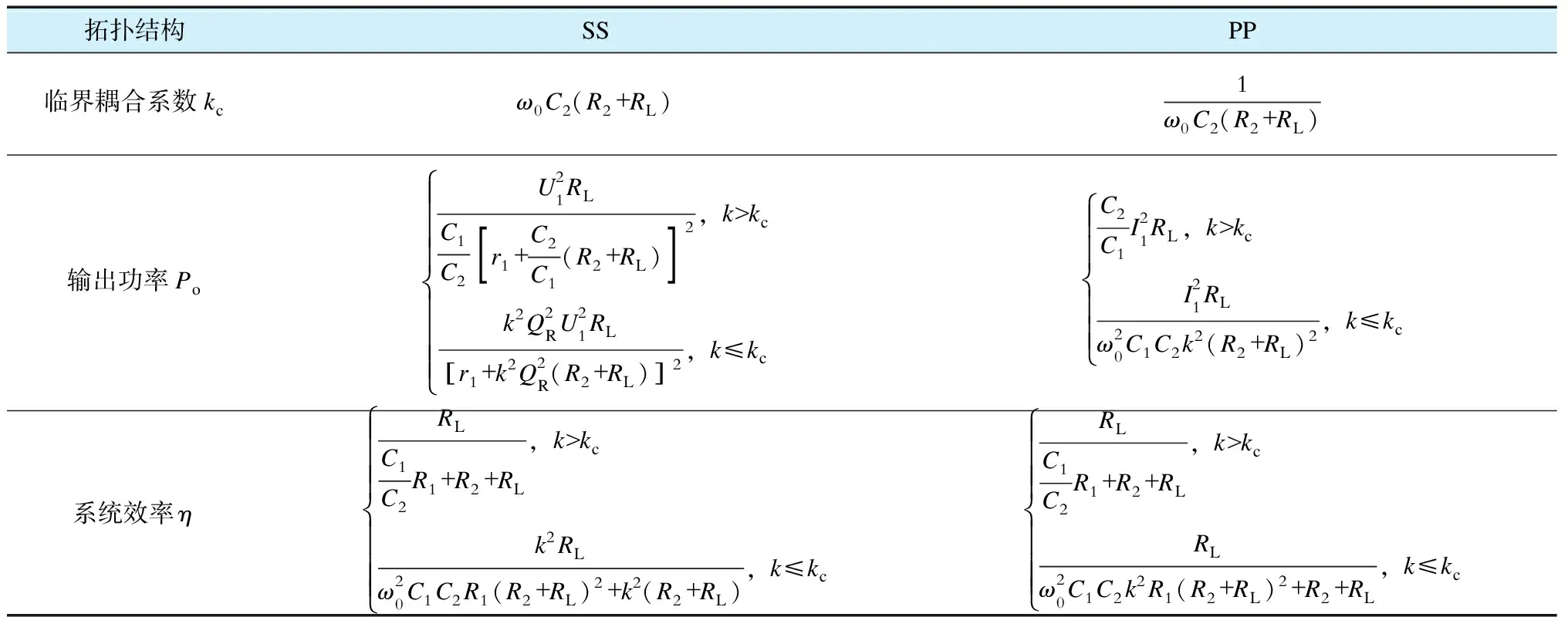
表1 基于PT对称的SS型和PP型ECPT系统特性比较
对比2种拓扑结构的ECPT系统,两者的临界耦合系数互为倒数。这意味着对于同一对耦合极板而言,PP型拓扑结构适用于较高谐振角频率和较大负载电阻的PT对称ECPT系统;其谐振角频率越高、负载阻值越大,系统的临界耦合系数越小,PT对称条件更容易满足。而SS型拓扑则更适用于则较低谐振角频率和较小负载阻值的PT对称ECPT系统,其谐振角频率越低,负载阻值越小,系统的临界耦合系数就越小,PT对称条件也更容易满足。
除此之外,当k>kc时,2种拓扑结构的传输特性相一致,在k变化时均能保持恒功率和恒效率;而当k≤kc时,在其他条件相同而k发生变化的前提下,2种拓扑结构的输出功率和传输效率不再保持恒定值,而是呈现相反的变化趋势。
3 仿真验证
在Simulink仿真软件中对2种拓扑结构的ECPT系统进行仿真验证。常见的金属耦合极板的电容值一般在数百pF到数nF之间,在本文仿真中系统的极板电容取2 nF。
根据第2章中对2种拓扑结构的ECPT系统的分析,对于同一耦合极板,为了使得系统对应的临界耦合系数较小(kc<0.1),SS型ECPT系统中选取较小的谐振频率和负载电阻,在仿真中设为f=300 kHz,RL=15 Ω;PP型ECPT系统中则选取较大的谐振频率和负载电阻,在仿真中设为f=2 MHz,RL=500 Ω。2种拓扑结构的两侧电路损耗相同,均设为2 Ω;系统的补偿电感值则由相应的谐振条件求得。2种拓扑结构的ECPT系统的参数设置见表2。

表2 基于负电阻的ECPT系统仿真元件参数
同时,仿真中耦合系数的变化范围为0.02~0.3, 以便模拟系统金属极板之间耦合情况的变化。基于PT对称的PP型ECPT系统的仿真结果如图7所示。
由所设置参数可计算PP型ECPT系统的临界耦合系数为kc=0.079。图7(a)为k=0.15时输入输出的电压和电流波形,输入电流为矩形波,幅值为0.2 A,输入电压为正弦波且与输入电流保持同相位,工作频率为2.144 MHz。图7(b)中,系统工作频率f随耦合系数k变化而变化:在k>0.079区域,ECPT系统工作在高频率分支;在k<0.079区域,ECPT系统的工作频率为系统固有谐振频率2 MHz。
图7(c)为系统输出功率Po随耦合系数k变化曲线:当k>0.079时系统输出功率恒定在16.2 W附近,与理论值一致;当k<0.079时,系统输出功率逐渐增加。图7(d)为系统传输效率η随耦合系数k变化曲线:当k>0.079时系统传输效率也能保持在恒定值,由于负载RL较大其系统损耗可以忽略不计,效率保持在99.2%左右。仿真值与理论值基本吻合,验证了所提系统具有恒功率恒效率的特性。
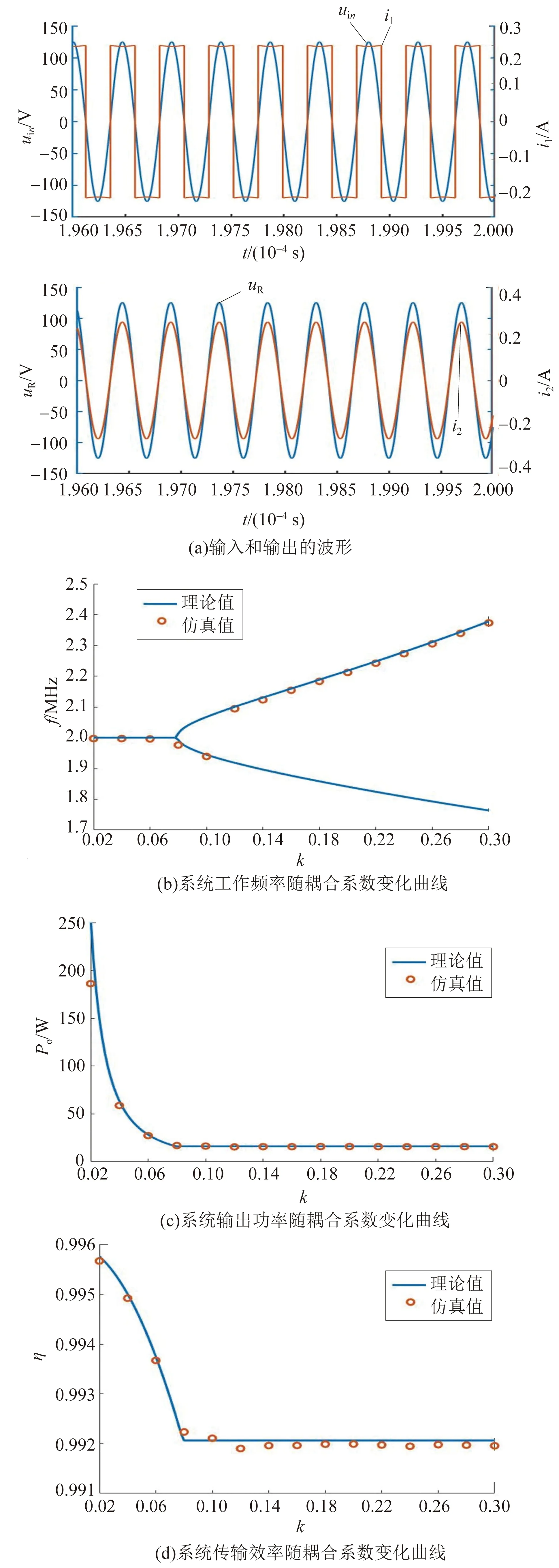
图7 PP型ECPT系统仿真结果
同样地,基于PT对称的SS型ECPT系统的仿真模型和结果如图8所示。
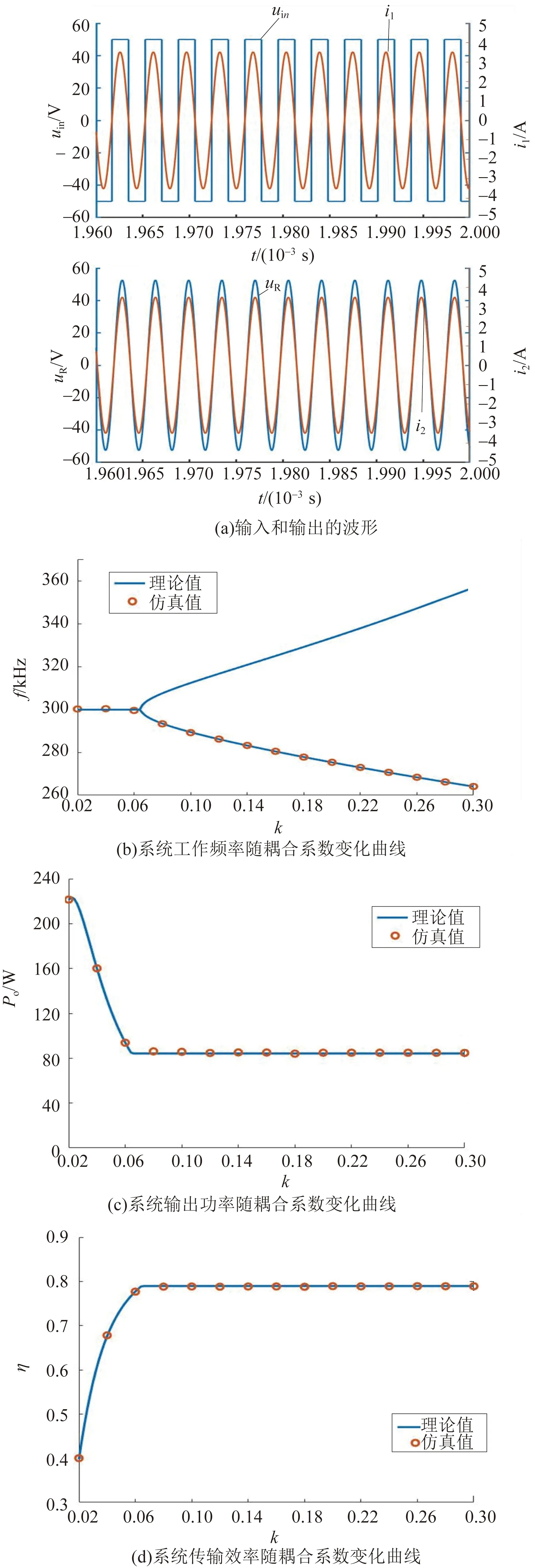
图8 SS型ECPT系统仿真结果
同样结合仿真参数可以求得SS型ECPT系统的临界耦合系数为kc=0.064。图8(a)为k=0.15时输入输出的电压和电流波形。可以看到,与PP型ECPT系统不同,系统输入电压为矩形波,幅值为50 V;输入电流为正弦波,与输入电压保持同相位;工作频率为280.98 kHz。图8(b)为系统工作频率f随耦合系数k变化曲线:当k>0.064时系统工作频率f随耦合系数k变化而变化,系统工作频率处于低频率分支;在k≤0.064区域,ECPT系统的工作频率为系统固有谐振频率300 kHz。图8(c)为系统输出功率Po随耦合系数k变化曲线,当k>0.064时,ECPT系统输出功率保持在84.2 W左右,这与理论计算值仍相符合。图8(d)中,当k>0.064时系统的传输效率η仍能保持在恒定值,由于负载RL与所设的两侧电路损耗较为接近,此时系统效率偏低,约为78.9%。若能降低两侧电路的固有损耗,系统的传输效率可进一步提高。对比仿真结果和理论计算值,所提系统的恒功率恒效率特性均得到了验证。
为了进一步分析2种拓扑结构下的系统增益,列出PP型ECPT系统的电压波形和SS型ECPT系统的电流波形,分别如图9和图10所示。
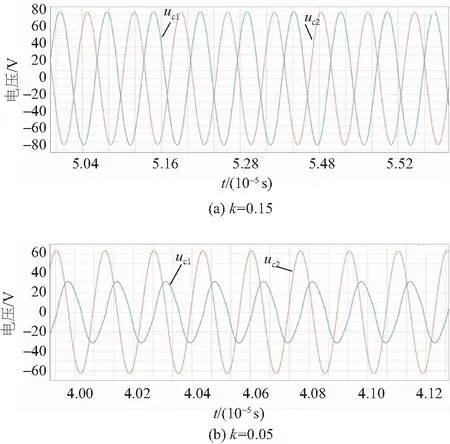
图9 不同耦合系数下PP型ECPT系统电压波形
图9为发射侧极板和接收侧极板两端电压uc1和uc2的波形。图10为发射侧和接收侧回路电流i1和i2的波形。可以看出当k=0.15,即系统处于PT对称态时,PP型ECPT系统两侧回路的极板电压幅值相等,SS型ECPT系统两侧的回路电流幅值也基本相同。而当k=0.05时,系统处于破碎的PT对称态,PP型ECPT系统的电压增益和SS型ECPT系统的电流增益与耦合系数k有关,其数值关系分别与式(18)、式(33)中的分析基本符合。
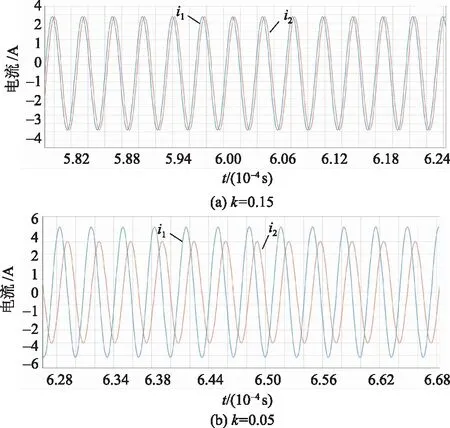
图10 不同耦合系数下SS型ECPT系统电流波形
4 结束语
本文提出了一种基于PT对称的ECPT系统,推导并分析了不同补偿结构(SS与PP)的ECPT系统的建模过程,结合不同补偿拓扑给出系统相应的负电阻实现方式。通过电路理论,研究并分析了2种系统相应的PT对称条件、工作频率特性和传输特性。在PT对称条件下,耦合系数变化时所提系统仍能保持恒功率和恒效率,且发射侧与接收侧无须通信。通过Simulink仿真验证了上述理论分析。本文提供了一种在耦合极板传输距离变化时实现ECPT系统恒定传输功率的解决方案,可为动态无线电能传输提供设计参考。

