基于二维主成分分析法的变压器声纹特征参数融合方法

孙安青，贾廷波，王丰华，杨秀龙，岳美，许景华

(1.国网山东省电力公司日照供电公司，山东 日照 276800；2.电力传输与功率变换教育部重点实验室(上海交通大学)，上海 200240)

作为电力系统中承担电压、电流变换及电能分配和传输的重要设备之一，变压器在保障电力系统安全、可靠、经济运行等方面发挥着重要作用。但是受使用年限增加和复杂运行环境等多种因素的影响，运行中的变压器故障不可避免，除了影响其使用寿命外，还会引发停电事故，导致人员伤亡等，造成难以估量的损失[1-3]。运行中变压器的状态监测一直是研究热点，这对提升电力设备运维水平和助力“双碳”目标意义重大。

变压器故障分为机械故障、绝缘故障和过热故障等，这些故障在发展演变过程中均会有声信号产生，如源于绕组、铁心及冷却系统等的机械振动声波，绝缘击穿时的放电声及过热引起的绝缘油沸腾声等。此外，还会有变压器机械紧固件的松动噪声、与其他部件的共振声，以及变压器直流偏磁引发的啸叫声等[4-5]。这些声信号可利用麦克风传感器或录音设备方便获取，已成为变压器状态监测领域的关注热点，其中如何对变压器声信号进行特征提取是关键。现有研究大多使用诸如声信号幅值和声压级[6-7]及傅里叶变换[8-9]、小波分析法[10-11]、自适应噪声完备集合经验模态分解方法[12]、稀疏自适应S变换[13]等时频分析方法获取变压器声信号特征参数，并据此基于支持向量机、支持向量数据对变压器过载、局部放电和机械振动引发的异响进行分类或识别。鉴于运行中的变压器声信号与语音信号有一定的共性特征，也有研究者从人耳对不同频率声信号的感知能力出发，将Mel频率倒谱系数(Mel frequency cepstrum coefficient，MFCC)、伽马通滤波器倒谱系数(Gammatone filter cepstrum coefficient，GFCC)等引入到变压器声信号特征提取中[14-17]，进而识别变压器绕组松动、铁心松动等典型故障。然而，受制于变压器的复杂结构、故障类型的多样性及声信号在空气中传播时相关干扰分量的不可预知性、环境噪声等多种因素，如何从非平稳的变压器声信号中提取出准确全面、具备一定抗干扰能力且对变压器不同状态区分度高的特征参数，仍然是变压器声信号监测技术的关键。

在语音识别领域，与使用三角滤波器组对语音信号进行特征提取的MFCC特征参数类似，常Q倒谱系数(constant Q cepstrum coefficient，CQCC)法基于常Q滤波器并根据音色特征分析语音信号，其滤波器组的中心频率按指数规律分布，滤波带宽不同，且中心频域带宽比为常数Q，可在有效避免时频分辨率均匀的同时获取分辨率更高的低频信号，并且能较好地跟踪声信号中的音色变化。为获取更为全面且具有一定抗干性能的变压器声信号特征参数，本文综合使用MFCC和CQCC特征参数分析变压器声信号，并引入二维主成分分析(two-dimensional principal analysis，2DPCA)对这2种特征参数降维和去冗余处理。最后以某变压器直流偏磁下的声信号为例进行分析，以验证所提方法的有效性。

1 变压器声纹特征参数

1.1 声信号预处理

由变压器的基本机械结构、工作环境及声信号的辐射特性可知，变压器的声压级会因测试位置不同发生变化，同一测试位置声压级也会因电压波动及负荷变化而发生变化。为避免声信号幅值对变压器运行状态判别结果的影响，需要对变压器声信号进行归一化处理，如下：

(1)

式中s(n)和x(n)分别为归一化前后的声信号，其长度为N0，1≤n≤N0，max和min分别表示s(n)的最大值和最小值。

同时，为有效提取变压器声信号的局部信息，需要对其进行分帧加窗。每帧信号长度需要综合考虑声信号的平稳性和计算效率，并保证每帧信号之间平稳过渡。对分帧信号进行加窗的目的是平滑时域信号，以满足傅里叶变换处理对信号周期性的要求。为降低截断引起的频谱泄漏，减小截断边沿处因信号突变产生的额外频谱，本文采用汉明窗，如下：

(2)

式中L为窗函数长度。

1.2 MFCC特征参数

MFCC是基于人耳听觉特性提出的声纹特征参数，通过将信号频谱转换到Mel频域内再进行倒谱分析。对预处理后的变压器声信号来说，其MFCC特征参数的提取过程如图1所示[16]，图1中，DFT表示离散傅里叶变换，p为Mel滤波器个数。Mel滤波器组由1组中心频率为f(i)的三角带通滤波器构成，其频响曲线如图2所示。由图2可见，Mel滤波器组在低频段通带较窄且分布密集，随着频率升高滤波器的通带逐渐变宽、分布也逐渐稀疏。因此，使用Mel刻度进行刻画的MFCC特征参数较好地描述了人耳对声信号的感知能力，对声信号的低频段信号更为敏感。

图1 MFCC特征参数提取过程

图2 Mel滤波器组频响曲线

当Mel滤波器个数为p时，输入信号经过Mel滤波器滤波后可得到p个参数mi(i=1,2,…,p)，对其进行求对数和离散余弦变换，可得到MFCC系数[16]

(3)

式中v=1,2,…,V，V为特征参数的维数。

1.3 CQCC特征参数

CQCC是在常Q变换(constant Q transform，CQT)基础上提取的声信号倒谱系数特征，CQT起源于乐音识别，本质上是使用中心频率与带宽比为常数Q的滤波器组。图3为CQCC特征参数提取过程，图3中，l为均匀重采样后的频带，XCQ(k)为对预处理后的输入信号进行CQT变换后的频域信号[18]，即

图3 CQCC特征参数提取过程

(4)

(5)

(6)

式中：k=1,2,…,K，K为CQT谱中划分的频带数目；Nk为窗长；fk为CQT谱中的第k个频率分量；fmin和fmax分别为所关注的信号频段的下限和上限频率；b为1个8度频率范围内划分的频率分量数目；fs为信号的采样频率。

均匀重采样是为了使对数能量谱呈现线性分布，处理过程为：在第1个8度音阶上确定一个线性重采样间隔Δfkl-1，其中，kl=1,2,…,K，将其分成带宽为Δfkl-1的d等份，由于高8度音阶频率范围是低8度音阶的2倍，故第3个8度音阶被分为2d等份，以此类推，第j个8度音阶被分为2j-1d等份。对重采样后的对数能量谱进行离散余弦变化即可得到变压器声信号的CQCC特征系数，为

(7)

式中q为均匀重采样后的频带数目。

CQCC特征参数由于采用了常Q滤波器组对声信号进行处理，不仅具有较高的低频分辨率，还可以较好地跟踪快速变化的泛音，有助于进一步提升变压器在不同状态下声信号特征参数的区分能力。

1.4 2DPCA特征降维

经MFCC和CQCC计算得到的变压器声信号特征参数具有区分度高、抗干扰能力强以及能够跟踪声信号音色快速变化等优点，但2种特征系数中亦包含了对不同运行模式的变压器声信号分类无益的冗余信息。故本文进一步基于2DPCA法对2种声纹特征参数进行融合降维，旨在提取变压器声信号主要声纹特征的同时，降低声纹特征数据的维数[19]。

设由MFCC和CQCC特征参数拼接组成的变压器声信号联合特征矩阵为F，此处，F由MFCC和CQCC特征参数列向量串联组成。首先求解F的协方差矩阵，为

(8)

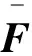
(9)

根据列方向投影矩阵U计算联合特征矩阵F降维后的特征矩阵R，

R=UF.

(10)

为定量描述经2DPCA降维后的声纹特征矩阵R对变压器不同运行状态声信号的区分能力，本文在此定义平均类间区分度DR=[DR1,DR2,…,DRm]，其中，m为特征数目，DRi为第i个特征的平均类间区分度。平均类间区分度为变压器某个状态声信号特征的类间离散度与类内离散度之比[20]，即

(11)

(12)

(13)

式中：M为变压器的样本类别数目；N为每类样本的数目；μh为第h类样本中特征向量x的平均值；μ为所有样本中特征向量x的平均值；xh,n0为第h类样本中第n0个样本的特征向量。

DRi≤1表示所获取的特征xi无法区分不同类型的信号，DRi>1表示特征xi能够区分不同信号，且DRi越大，表示特征xi对不同类信号的区分度越高。

2 变压器声信号获取

以2台型号为DSP-223000/550的500 kV变压器为试验对象，基于循环电流法，通过改变变压器分接档位以产生环流，进行直流偏磁下的负载试验。注入变压器高压侧的直流电流分别为0、1 A和1.8 A。测试用麦克风传感器为2个灵敏度为50 mV/Pa的AWA14423-1/2型测试电容传声器，放置位置参照电力变压器噪声测试分析标准GB/T 1094.10—2008《电力变压器 第10部分：声级测定》，即放置在距离其中一台试验变压器低压侧1 m处，对应的轮廓线为试验变压器高度的2/3，采样频率为50 kHz。

限于篇幅，同时为避免试验大厅墙壁及周边障碍物对声信号的折反射影响，本文在此给出其中1个测点处的变压器声信号及其频谱分布，分别对应注入直流电流(用IDC表示)0、1 A和1.8 A的情形，如图4所示。由图4可见，变压器声信号呈现非线性和非平稳，其频谱分量较为丰富，包含了大量50 Hz的奇数次倍频和偶数次倍频，且主要集中在700 Hz以内。有直流分量注入到变压器绕组中后，声信号的时域幅值随之增大，400 Hz和450 Hz分量的占比明显增大，且其分布随直流分量的改变而变化。

图4 变压器不同偏磁电流下的声信号

3 结果分析

对图4所示的变压器声信号分别计算其MFCC和CQCC特征参数及类间区分度，结果分别如图5和图6所示。计算时采用的声信号时长为5 s，以长度为200 ms的汉明窗对变压器声信号进行分帧，相邻帧之间存在50%的重叠，采用24个Mel滤波器和常Q滤波器计算MFCC特征参数和CQCC特征参数。此外，在计算CQCC特征参数时，令每个8度频率范围内的谱线数b=96，线性重采样的间隔数d=1。另外，对应的MFCC和CQCC系数分别根据式(3)和式(7)计算得到。

图5 不同偏磁电流下MFCC特征参数与类间区分度

由图5可见不同直流偏磁作用下的变压器声信号的MFCC特征系数形状相似，但全部24维特征参数的幅值存在明显差别。此外，共有9维特征的类间区分度小于1，其余15维特征的类间区分度大于1，平均类间区分度达2.8，这表明MFCC系数对变压器不同直流偏磁下的声信号具有一定的区分性。其中，第1、3、12维特征的类间区分度明显高于其他特征，分别为16.1、8.8和5.9。由图6可见，与MFCC相似，CQCC特征系数随维数增加也呈波浪状，不同直流偏磁电流作用下的声信号各维特征幅值存在明显差别。在24维CQCC特征系数中，共有16维特征的类间区分度大于1，其余8维特征的区分度小于1，其中第1维和第9维特征的类间区分度较高，分别为22.4和5.9。此外，CQCC系数中具有区分性的特征系数多于MFCC，最大区分度也高于MFCC，但除第1维特征外，其余特征的整体区分水平略低。

图6 不同偏磁电流下的CQCC特征参数与类间区分度

图7为经2DPCA降维后的变压器声纹特征参数，计算时取累计贡献率ρ=0.99。由图7可见，融合后的变压器声纹特征参数维度降至10维，数据量大幅降低。此时，不同偏磁电流作用下的特征参数存在明显区别，10维融合特征的类间区分度均大于1，其中第1维和第4维特征具有明显高于其他特征的类间区分度，分别为27.4和17.7，是融合特征中的主要区分性特征。显然，2DPCA所保留的变压器声纹特征参数主成分均为区分性特征，而对区分其运行状态没有贡献的冗余信息在降维过程中均被舍弃。

图7 2DPCA降维融合后的特征参数与类间区分度

MFCC特征参数、CQCC特征参数，以及经2DPCA降维融合后的特征参数对于不同直流偏磁下变压器声信号的平均类间区分度分别为2.8、2.7和8.3。由此可知，MFCC特征系数和CQCC特征系数的平均类间区分度水平相当。而2DPCA在2种声纹特征的基础上进行融合降维，保留了原特征中的区分性信息，去除了其中的冗余成分，特征的平均类间区分度达8.3，高于单一的MFCC特征参数和CQCC特征参数的类间区分度。这说明本文所提取出的变压器声纹融合特征对不同运行状态的变压器声信号具有更好的区分性。

为说明变压器声信号融合特征参数的抗噪能力，本文从NosieX-92噪声库中选取变电站现场常见的白噪声、背景说话人噪声及工业噪声混入经试验获取的变压器声信号中，分别计算MFCC特征参数、CQCC特征参数及经2DPCA降维融合后的特征参数对于含噪变压器声信号的平均类间区分度，结果见表1。由表1可见，噪声信号的引入不会对本文所提声信号融合特征参数的类间区分度产生影响，即使信噪比降低为0。且在3种噪声测试情形下，本文所获取的融合特征参数的平均类间区分度均最高，表现出了较好的抗干扰能力。

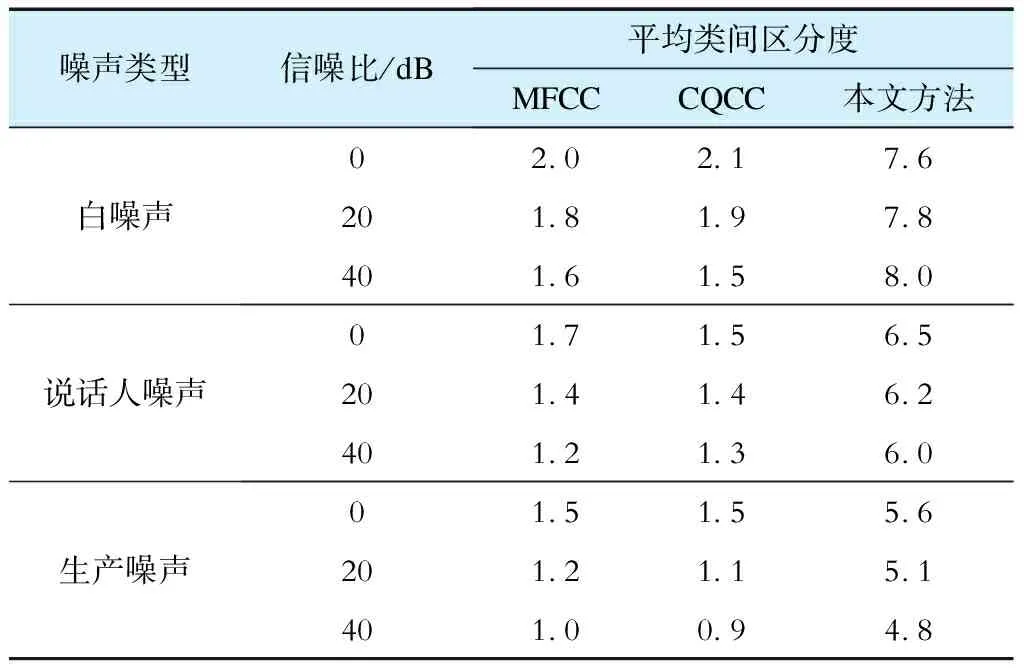
表1 含噪声信号的不同特征平均类间区分度

为进一步说明所获取的融合特征参数的有效性，表2给出了对应于变压器2种偏磁电流(IDC)作用下的特征参数的平均类间区分度。

表2 变压器不同状态间特征参数的平均类间区分度

由表2可见，变压器相同状态的声信号特征参数应一致，其区分度为0，正常状态与直流1.8 A作用下的区分度最大，直流1 A与直流1.8 A作用下的状态间的区分度次之，正常与直流1 A的区分度最小。显然，这一结论与变压器直流偏磁下振声作用机制吻合良好，即随着注入变压器绕组电流直流分量的增加，变压器的工作点会进一步接近于其磁化曲线的拐点，致使变压器受磁滞伸缩力及电磁力作用的铁心振动加剧，声信号进一步增强[21]。此外，基于声信号融合特征参数计算的类间区分度均优于单一MFCC特征或CQCC特征，可作为变压器直流偏磁耐受能力评估的重要依据，亦可为变压器运行状态的监测分析提供更好的数据支持。

4 结论

变压器声信号的MFCC、CQCC及其融合声纹特征参数的计算结果表明：

a)MFCC和CQCC特征参数均有效反映运行中的变压器声信号在不同频段上的能量特征，并捕捉变压器的运行状态变化，但对应的声纹特征中包含若干冗余信息，且总体区分度较低。

b)所提出的基于2DPCA的变压器声纹融合特征提取方法能够有效保留MFCC和CQCC中的特征信息，相比于单一的声纹特征对变压器不同直流偏磁状态下的声信号区分度更高，且数据维度低。

后续研究中将进一步积累变压器声信号，验证所提声纹特征参数融合方法的有效性，并将其用于变压器运行状态监测与识别中。