基于修正层次分析法的多阶段PMU最优配置

席禹，于力，蒋文辉，陈波，周波，梁博，张家兴

(南方电网数字电网研究院有限公司，广东 广州 510700)

当前的电网已经形成高度互联、规模庞大的系统，若其中某一部分受到干扰，可能会对整个系统稳定运行造成影响[1-2]。电力系统的可观测性是进行状态估计的必要条件，也是广域监测保护与控制系统有效实施的前提。作为广域测量系统(wide area measurement system，WAMS)的重要组成部分，相量测量单元(phase measurement unit，PMU)能够测量节点上的电压相量，根据自身容量测量节点有限数量的分支电流相量，并基于全球定位系统(global positioning system，GPS)的参考时钟提供同步电压相量、电流相量、频率及其变化率等。

从PMU接收到的实时测量数据能够用于不同的电力系统应用，如状态估计、暂态和动态稳定性分析、电压稳定性监测[3-6]。但PMU安装成本较高，目前仅能选择部分节点进行PMU配置，因此需要对配电网的PMU配置进行优化，最大程度地减少PMU的数量并保持配电网的完全可观性。文献[7]总结了最优PMU配置(optimal PMU placement，OPP)模型求解的主要方法及其优缺点，如整数线性规划、模拟退火法、遗传算法等。文献[8]提出一种改进的图论法，根据网络形成最优生成树，并基于生成树选择PMU的最优位置，实现网络的完全可观。文献[9]结合零注入节点的特性，提出基于整数规划算法的PMU优化配置算法，以更少数量的PMU实现整个网络可观。

在电力系统网络中，需要制订分阶段的PMU配置计划。文献[10]提出基于分阶段的PMU配置的模拟退火公式，比单阶段配置需要更多的PMU。文献[11]提出了新的PMU布局方案，保证了网络关键节点的监控和保护，以及网络的完全可观测性。然而，文献[10-11]没有考虑通道限制和关键节点供电能力对多级PMU布置的影响。

针对上述研究的不足，考虑到配电网系统中发生线路或PMU“N-1”故障时仍需要保持系统完全可观测，本文采用修正层次分析法(revised analytical hierarchy process，RAHP)，提出一种基于电压稳定性监测的多阶段PMU配置方法。首先确定配电网完全可观测所需的最小PMU数量，然后根据快速电压稳定指数(fast voltage stability index，FVSI)识别关键母线。为了在配置PMU的第1阶段就监测到关键母线，本文采用RAHP来分阶段配置PMU，并在决策过程中引入关键母线可观测性指标(critical load bus observability criteria，CLOC)来确定关键母线的最大优先级。

1 PMU配置

配电网中存在大量负荷节点，当所有节点都能被至少1个PMU直接或间接观测到时，则配电网完全可观。

1.1 PMU配置规则

PMU配置规则见表1，下面结合图1所示的不同节点连接方式进行说明。

以图1(a)为例：若节点1配置了PMU，根据规则1，该节点的电压相量及所有出线电流相量可由PMU测量得到；支路1-2、1-3的支路电流及节点1的电压相量均能被测得，根据规则2可计算出节点2、3的电压相量；若节点2、3电压已知，根据规则3可计算出节点2、3之间的支路电流。

实际配电网中会存在部分零注入节点，零注入节点的所有出线电流之和为0，是另一个可能减少PMU数量以实现完全可观性的因素。该节点存在的情况下，可以根据表1中的规则4—规则6来评估网络的可观测性。以图1(b)为例，其中节点i是与节点{1,2,3,4}相连的零注入节点：假设节点{i,2,3,4}为可观测节点，节点1不可观测，根据规则4可以计算出支路i-1的电流；假设节点{1,2,3,4}为可观测节点，零注入节点i不可观测，根据规则5可以计算出节点i的电压相量。以图1(c)为例，所有节点都与零注入节点{i,j}相连，根据规则6可以计算节点{i,j}的电压相量。

表1 PMU配置规则

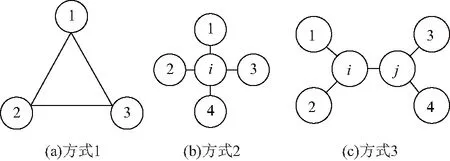
图1 PMU配置说明

上述规则能使零注入节点的相邻节点被识别为可观测节点，因此不需要为其配置PMU，从而减少网络中PMU的数量。

1.2 计及“N-1”故障下系统可观测的PMU配置

在实际运行中，配电网总会有发生故障的可能性。进行PMU配置时，需要确保配电网的某条线路或某个PMU发生故障时配电网依然完全可观。

a)线路“N-1”故障。若某线路发生“N-1”故障，要使配电网依然完全可观，可观测的节点i需要满足以下条件之一：①节点i配置了PMU；②节点i的相邻节点中至少有2个节点配置了PMU。

b)PMU装置“N-1”故障。假设PMU节点仅配置1个PMU，若某个PMU发生故障时，仍需保持系统完全可观，可观测的节点i需要满足以下条件之一：①节点i配置了PMU，并且其相邻节点中至少有1个节点配置了PMU；②节点i未配置PMU，其相邻节点中至少有2个节点配置了PMU。

综上，本文提出的PMU配置方法将使每个节点被至少2个PMU观测到，即使发生PMU装置或线路“N-1”故障，系统依然完全可观。

1.3 最优PMU配置公式

OPP是求解在电力系统中放置最小PMU集，以实现全网络可观测性，目标函数为

(1)

约束条件为

Ax≥b.

(2)

(3)

2 关键母线识别

为了确定配电网系统的最大负载能力，采用FVSI进行电压稳定分析。

2.1 线路FVSI

对于典型线路，FVSI计算公式为

(4)

2.2 识别关键母线的步骤

步骤1：使用牛顿迭代法运行基本情况下的潮流程序。

步骤2：计算基本情况下系统每条线路的FVSI值。

步骤3：在选定的负载母线上逐步增加无功负载0.01(标幺值)，保持其他母线负载不变，直到潮流解不能收敛，发散前的负载是该母线的临界负载。

步骤4：计算每个母线在临界负载条件下的FVSI值。

步骤5：在每个母线中提取最大可计算FVSI的最大无功负载，最大无功负载是指相应母线的最大负载能力。

步骤6：将步骤5中获得的最大负载能力按升序排序，排名越高表示母线的最大负载能力越低。

3 多阶段PMU安装

RAHP是PMU安装阶段的第2步，即确定最佳PMU位置后进行RAHP。而在中间阶段，配电网系统只能部分可观测，这段时间内PMU的配置应最大限度增加系统中的可观测母线和关键参数数量，从而获得最大的效益。在决策过程中，负载母线可观测性指标(load bus observability criterion，LBOC)等性能指标非常重要[14-15]。

3.1 负载母线可观测性指标

根据关键母线识别方案，将给定系统中的负载母线分为关键母线和非关键母线。

关键母线负载可观测性指标(critical load bus observability criterion，CLOC)的表达式为

(5)

非关键母线负载可观测性指标(noncritical load bus observability criterion，NLOC)的表达式为

(6)

图3为7节点系统的单线图，取Nc1、Nc2、Nc3分别为与母线K相邻的关键母线、关键母线的相邻母线、相邻母线的相邻母线的集合；按照关键母线的识别步骤，选取图3中的关键母线集合Nc1为{3,7}，则Nc2、Nc3分别为、{2,4,6}、{1,5}，PMU母线集合为{1,2,4,5}。连接母线1、2、4、5的母线集合分别为{2}、{1,3,7}、{3,5,6,7}、{4,6}，PMU母线的CLOC为：

图3 7节点系统的单线图

取Nn1、Nn2、Nn3分别为与母线K相邻的非关键母线、非关键母线的相邻母线、相邻母线的相邻母线的集合，Nn1、Nn2、Nn3分别为{2,4,6}、{1,3,5,7}、空集，PMU母线的NLOC为：

3.2 发电机可观测性指标

为了实现更紧密、实时的控制，需要对发电机母线进行观测，因此发电机母线的权重更高。PMU发电机可观测性指标(generator observability criterion，GOC)表达式为

(7)

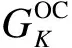
取Ng1、Ng2、Ng3分别为与PMU母线K相邻的发电机母线、发电机母线的相邻母线、相邻母线的相邻母线的集合，Ng1、Ng2、Ng3分别为{1,5}、{2,4,6}、{3,7}，PMU母线的GOC为：

3.3 PMU分配指标

安装PMU时，应使其尽量稀疏地分布在电网中。母线i和j之间的电气距离

eij=eji=-lg(αijαji),

(8)

(9)

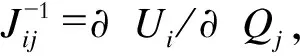
PMU母线K的PMU分配指标(PMU distribution criterion，PDC)值

(10)

式中m∈NP，NP为配置了PMU的母线集合。

3.4 联络线可观测性指标

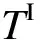
3.5 母线可观测性指标

PMU母线可观测性指标(bus observability criterion，BOC)等于与其相连的母线总数，PMU母线K的BOC值

(11)

式中BKj为0-1变量，如果PMU母线K直接与母线j相邻则BKj=1，否则BKj=0。

4 RAHP

RAHP是一种通过两两比较进行测量的理论[17]，它依赖于专家的判断得出优先级尺度，流程如图4所示。

图4 RAHP的流程

CLOC、GOC、TOC、NLOC、PDC及BOC分别为权重C1、C2、C3、C4、C5、C6，通过将权重进行两两比较形成总体偏好矩阵

其中Ci/Cj是权重的相对比较，其值为1～9，值越大表示Ci的优先级较Cj越高。

矩阵C的一致性检验如下：

CI=(λmax-n)/(n-1).

(12)

CR=CI/RI.

(13)

式中：CI为一致性指数；CR为稠度比；λmax为矩阵C的最大特征值；n为指标数量；RI为平均随机一致性指数，为经验值，n=6时RI=1.24。本文计算的CR=4.38%，远低于一致性限制(10%)。

(14)

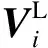
若备选方案k可用于最优PMU配置，定义Vki为与备选方案k相关联的指标i的标准值。备选方案k的PMU配置指数(PMU install index，PMII)计算公式为

(15)

图5 7节点系统的归一化权重和PMII排名

假设7节点系统的PMU安装共分2个阶段进行，每个阶段配置2个PMU。阶段1将PMU放置在母线4、2上，使系统完全可观测。阶段2将PMU放置在母线5、1上，使得系统的每条母线都能被2个PMU观测，并且线路中断和PMU故障不会影响网络的完全可观测性。

5 算例分析

5.1 最优PMU位置

采用本文提出的基于RAHP的PMU优化布置方法，以图6所示的IEEE 34节点系统为配电网模型进行仿真，结果见表2。

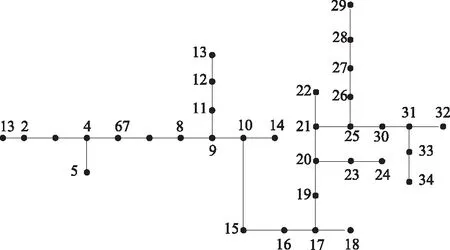
图6 IEEE 34节点系统

表2 IEEE 34节点系统完全可观测性的最佳PMU位置

5.2 多阶段PMU配置

按照2.2节的步骤进行负载母线排序，结果如图7所示。负载母线26排名为1，最大负载能力1.192 Mvar。本文将排名前4位的负载母线作为关键母线，即26、18、17、15。

图7 IEEE 34节点系统的负载母线排序

PMU配置分3个阶段进行，每个阶段有4个PMU。表3给出了IEEE 34节点系统的分阶段配置顺序：第1阶段，所有关键母线均配置PMU，以监测和控制电压稳定；第2阶段，通过配置另外4个PMU，使系统完全可观测；第3阶段，安装所有12个PMU，使母线被至少2个PMU观测。即使PMU发生故障或线路中断，也能够保持系统完全可观测。

表3 IEEE 34节点系统的多阶段PMU配置

5.3 算法结果对比

为了验证该方法的优越性，以IEEE 34节点系统为例，将本文所提的方法与其他算法进行比较，见表4。

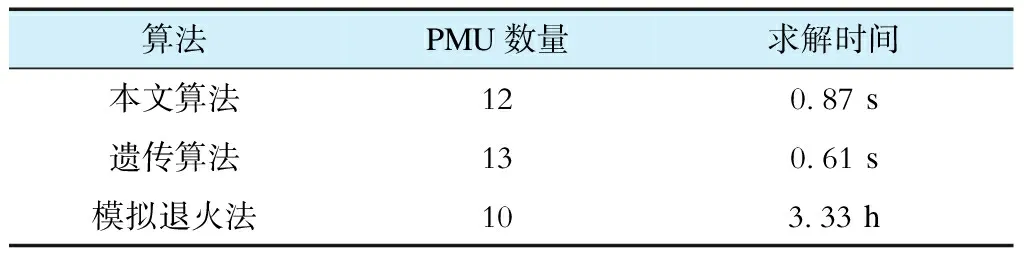
表4 不同算法结果比较

由表4可知：模拟退火法求解出的最优PMU数量虽然最少，但该算法的收敛速度极慢，求解用时过长，在电网中的实用性较低；遗传算法求解时间最短，但该算法的全局收敛能力较差，容易收敛到局部最优解；本文提出的方法在经济性和时间效益方面均有良好的效果，以较少的PMU配置数量实现系统的完全可观测，求解时间也较短。此外，与传统的一次性PMU配置法相比，本文提出的多阶段PMU配置方法充分考虑了配电网中需要重点监测的区域，具有一定的优势。

6 结束语

本文基于RAHP提出了多阶段PMU配置方法，用于监测电力网络中的电压不稳定。首先考虑配电网系统中发生支路中断或PMU故障情况，确定配电网完全可观测所需的最小PMU数量，然后利用FVSI确定关键母线，并通过RAHP对最优PMU位置进行排序，按排序结果分阶段对PMU进行配置。采用IEEE标准系统进行仿真，验证了本文方法的正确性与有效性。