基于YOLOv4及金字塔LK光流法的变压器振动检测方法

苏磊, 黄华, 秦伦明, 赵文彬

(1.国网上海市电力公司电力科学研究院，上海 200437；2.上海电力大学 a.电子与信息工程学院；b.电气工程学院，上海 200090)

为了响应国家大力发展新能源发电的号召，越来越多光伏电站和风电场接入电网，但其在缓解能源匮乏和环境污染的同时，也给电网带来了诸多威胁，尤其是一些新能源电站为节约成本，要求直接接入变电站低压侧，再通过变电站向更高电压等级变电站输送电能。因此，新能源对电网的不利影响便会直接施加在变电站中的电力变压器上。变压器作为电力系统的上游关键设备，不仅价格昂贵，还承担着电压变换、电能分配和传输等任务，其运行可靠性影响着电网的运行安全。变压器一旦发生故障，可能导致大规模停电事故，造成巨大的直接和间接经济损失[1]。因此，研究电力变压器的早期故障检测及健康状态评估对提高电力变压器可靠性，保证电网安全稳定运行具有极为重要的意义。

随着智能化技术的进步[2]，对变压器的维护逐渐采用状态检修代替传统的定期检修和事故后维修。状态检修主要根据对变压器运行状态的监测结果确定维修策略，从而缩减设备维修成本，降低停机损耗并有效预防故障的发生[3]。当前，变压器状态评估方法主要分为在线监测和离线检测2大类。在线监测时变压器不需要停止运行，能够节省人力、物力，具有明显优势。常用的电力变压器在线监测方法主要有低压脉冲法、频率响应分析法、变压器油中溶解气体的气相色谱分析法、局部放电在线监测法以及振动分析法等[4]。其中振动分析法的一大优点是检测系统不与被测变压器发生任何形式的电气连接，不会影响电网的正常运行，充分保障了在线监测的安全性，并且克服了频率响应分析法、短路电抗法等只能离线监测变压器机械故障的不足。振动分析法属于体外检测分析方法，利用振动传感器获取变压器油箱表面的振动信号，进而提取其中包含的时频域特征，实现变压器在线状态监测。20世纪90年代中后期，基于振动分析法进行变压器运行状态在线监测的设想被提出，虽然目前仅有俄罗斯将该方法应用到现场，但使用结果证明振动分析法可用于任何类型的变压器，且准确率相对较高。由于未深入研究绕组和铁心的振动特性，且缺乏经验，该方法在监测绕组和铁心故障时仍有很大局限性[5-6]。

针对变压器振动分析法的深入研究:Berler等对变压器进行空载和负载对照试验，获得了铁心和绕组单独作用时变压器箱体的振动，将实验室研究向前推进了一大步[3];Garcia和Burgos等研究了振动幅值和相位与运行电压、负载电流、温度之间的关系，建立了基频振幅与运行电压、负载电流、温度三者的数学模型，并得到绕组和铁心振动基频幅值分别与负载电流、运行电压的平方成正比的关系，该结论对后续变压器研究起到了重要的指导作用[7-8]。

变压器振动信号检测是分析和评判变压器运行状态和故障诊断的重要前提。目前，振动信号检测广泛应用于机械、车辆、建筑、航空航天等各类工程中，已经成为工程测量领域中的重要研究方向[9]。振动信号的检测方法大体可分为接触式测振和非接触式测振2类。传统接触式测振主要采用现场安装传感器的方式，由于需要逐点布置，测量范围有限，且进行位移监测时还需要寻找固定的参照物或参考点，该方法存在诸多缺陷。常用的非接触测振主要有激光测振和基于视频图像的视觉测振方法2类。激光测振方法主要依据光的干涉原理，具有精度和灵敏度极高、测量距离远、测量频率高等优点。当前激光测振相关设备售价均非常昂贵，对操作人员专业性的要求也较高，极大制约了其大范围推广和应用，目前常用于航空航天和机械制造领域。基于视觉的振动检测作为新兴的振动测量方法，受到国内外学者的广泛关注[10-19]。视频图像监测是一种既能进行位移、应变等静态测量，也适用于动态特性测量的非接触式监测方法，具有操作简便、非接触、无损、不产生附加质量、可实现远距离大范围多点监测等优点，但也存在需要设置标靶、监测设备要求高、对环境光线和背景要求高等问题。

针对上述研究的不足，本文提出一种基于视频的振动检测方法，旨在实现高比例可再生能源接入情况下变压器实时状态评估。基于变压器视频信号，首先利用迁移学习思想和YOLOv4模型检测图中变压器所在位置作为感兴趣区域(region of interest，ROI)，避免手动设置标靶。采用Shi-Tomasi方法在ROI内提取特征点，计算变压器振动矢量，从而避免环境光线、背景因素的干扰。为了提高变压器振动矢量的计算精度，采用金字塔LK(Lucas-Kanade)稀疏光流法计算感兴趣区域内所有特征点的振动矢量，然后使用大津算法(OTSU法)计算振动矢量的阈值，进而滤除模值较小的振动矢量。最后，对剩余的振动矢量进行求和平均，所得均值作为变压器振动矢量的最终结果。

1 研究背景

1.1 YOLOv4模型

YOLOv4是一种高效且功能强大的目标检测算法，结合了大量现有技术进行创新，以实现检测速度和检测精度之间的完美平衡。YOLOv4模型包括4个部分：输入(Input)、特征提取主干网络(BackBone)、特征增强网络(Neck)和预测网络(Prediction)，其结构如图1所示。

图1 YOLOv4模型结构

YOLOv4的特征提取主干网络为CSPDarknet53网络，是在Darknet53的基础上，结合跨阶段局部网络(cross stage partial network，CSPNet)改进得到的。CSPNet将梯度变化统一集成到特征图中，解决了其他特征提取网络梯度信息重复的问题，并减少了模型参数量和FLOPs数值。特征增强网络对来自主干网络的多个层级的特征图进行融合，增强其表达能力，并将图像特征输出到预测网络。YOLOv4的特征增强网络使用了空间金字塔池化(spatial pyramid pooling，SPP)结构以增大感受野，并使用路径聚合网络结构(path aggregation network，PANet)代替特征金字塔网络(feature pyramid network，FPN)进行参数聚合以适应不同层级的目标检测。YOLOv4的预测网络对提取的3个特征层进行预测，并对预测结果进行解码得到预测框的位置。此外，YOLOv4还使用了Mosaic数据增强、类标签平滑(label smoothing)、DropBlock正则化和学习率余弦退火衰减等训练策略，提升了模型性能。

1.2 金字塔LK光流法

1.2.1 基本假设

光流法研究的是连续图像中目标的位移情况，为此需要在2帧图像之间建立联系。光流法的实现需要2个基本假设作为前提：首先，图像强度不变。本文将彩色图像转为灰度处理，可理解为目标上某一像素点在图像上发生位移时，其灰度值不变。其次，目标运动幅度较小，也即目标位置在相邻2帧图像之间不会发生明显变化。基于这2个假设可以将2帧之间的同一目标联系起来。

1.2.2 约束方程

光流法所研究的基本问题用图2表示。图2中：I为某一像素点光强，其相关参数为空间位置(x,y)和时间t，即I(x,y,t)；在下一帧图像中，该像素移动了(dx,dy)的距离，间隔时间为dt。

图2 光流法研究问题示意图

依据1.2.1节中的第1个假设，建立如下方程：

I(x,y,t)=I(x+dx,y+dy,t+dt).

(1)

为了去除公共项，对式(1)等式右边部分进行泰勒展开后简化可得：

I(x+dx,y+dy,t+dt)=

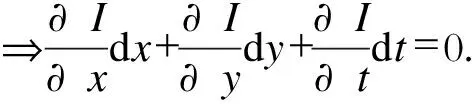
(2)

将式(2)除以dt得

(3)

式中u=dx/dt、v=dy/dt是需要求解的2个未知变量。∂I/∂x, ∂I/∂y、∂I/∂t分别为图像中像素点的灰度沿x、y、t方向的偏导数，可根据实际图像数据求出。由于只有1个约束方程式(3)，无法求解2个未知量，需要引入一些方法(如Lucas-Kanade算法)来解决这个问题。

1.2.3 LK光流法

主流光流算法可分为稠密光流法和稀疏光流法2类。稠密光流法会对图像上的每一个像素点进行匹配，计算其偏移量，对运动目标的配准精度较高，但计算量较大。本文采用的LK光流法是稀疏光流法中的一种典型算法，相较于稠密光流法，该算法不会对所有像素进行逐点计算，而是跟踪1组数量相对较少的特征点。这些特征点通常由一些特定的角点检测算法(如Shi-Tomasi算法)计算得出，用其表示目标的整体运动情况。

LK光流法在原光流法的2个基本假设上，新增了“空间一致”的假设，即在一定区域内相邻像素有着近似的移动。根据这个假设，可以在特征点周围划出一个N×N的小窗，并认定小窗内的所有像素点都有相同的移动，如图3所示。

图3 利用LK光流法对黑色像素点的光流进行估计

上述LK光流法可用以下公式来描述：

(4)

式中：q1,q2,…,qn为小窗内包含的像素(例如当窗口大小为3×3时，n=9)；Ix(qi)、Iy(qi)和It(qi)分别为像素qi的光强I在x、y、t方向上的偏导数；Vx=u=dx/dt为x方向上的移动速度，Vy=v=dy/dt为y方向上的移动速度。式(4)可用以下矩阵形式表示：

(5)

在基本的光流法中，因为只有1个约束方程，无法解出2个未知量。而在LK光流法中则出现了n个方程(n>2)，变成了超定方程组。利用最小二乘法求解该方程组可得：

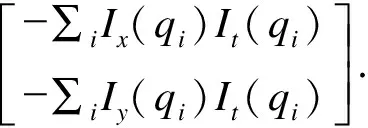
(6)

1.2.4 金字塔LK光流法

LK光流法是建立在物体运动幅度较小的假设之上，在1.2.2节计算约束方程的过程中，式(2)进行泰勒展开时只保留了一阶项，而当物体运动幅度较大时会出现较大误差。为此，使用金字塔法对LK光流法进行改进。

如图4所示，金字塔LK光流法通过对图像进行降采样，可在高层金字塔图像中缩小较大的位移，从而求得该尺度下较为准确的光流矢量。然后，从顶层逐层往下求解时按比例放大高层矢量作为下一层的初始指引。此时从高层放大的光流矢量所指引的目标位置和当前层的实际目标位置会存在误差，但该误差通常符合小运动的尺度，因此可在此基础上计算获得当前层的光流矢量，依次循环往下到达底层原图时可获得较为准确的大幅度运动下的光流矢量。

图4 采用金字塔法从金字塔最高层(细节最少)向最低层(丰富细节)进行跟踪

2 本文方法

2.1 变压器检测

首先读入变压器的振动视频，在首帧图像中检测出变压器的具体位置，以便后续在ROI内进行振动检测。本文结合迁移学习和YOLOv4目标检测模型进行变压器检测。由于变压器图片数量有限，如利用YOLOv4模型直接进行训练，容易因过拟合导致模型在测试集上的性能表现较差。本文借鉴迁移学习的思想，利用大型数据集对YOLOv4模型进行预训练，对训练好的模型权重进行迁移应用，建立YOLOv4迁移学习模型；利用该模型对首帧图像进行变压器检测，得到变压器的位置区域。

2.2 特征点检测

本文采用Shi-Tomasi方法计算特征点。由于变压器边缘以及外围区域的特征点与变压器振动无关，引入这些特征点容易引起干扰，有必要设定ROI作为特征点检测的范围。将第1帧图像转换为灰度图像，依据YOLOv4模型的预测结果，得到变压器位置及其中心点。本文按比例设定变压器中心的一块区域作为特征点检测范围，由此计算首帧中的变压器特征点作为初始特征点。另外可通过设定最大特征点数量、特征点质量水平、相邻特征点间最小距离、特征点运算区域尺寸等参数控制生成特征点的数量和质量。

2.3 变压器振动检测

利用金字塔LK稀疏光流法，根据首帧特征点以及后一帧图像计算得到特征点在2帧间的位移矢量。由于在计算过程中会出现不可避免的误差，不能简单地取其中1个特征点的位移矢量代表变压器整体的位移矢量。通常某一特定物体上会计算出多个特征点，而变压器可看作刚性物体，即变压器上的每一个特征点都会发生近似位移。

本文首先提取变压器特定区域内的特征点，通过金字塔LK稀疏光流法计算得到区域内所有特征点的位移矢量；然后计算所有矢量的模，使用OTSU法求解矢量模的阈值，进而滤除模值较小的振动矢量；最后对剩余的振动矢量进行求和平均，得到的均值即为变压器在图像中的最终振动矢量。将每2帧之间的变压器位移和时间间隔结合起来，即可计算得到变压器的振动速度；进一步利用双目视觉计算得到变压器在三维空间中的振动特性。

3 实验结果与分析

3.1 基于YOLOv4的变压器检测

3.1.1 实验环境

本文利用YOLOv4建立变压器目标检测模型，实验环境为Windows10、64位操作系统，CPU为 32核Intel Xeon E5-2695 v3，内存32 GB，GPU型号为NVIDIA Grid P40-24Q，NVIDIA驱动版本为441.66，显存大小为24 GB。使用的深度学习框架为TensorFlow-GPU 2.2，CUDA版本为10.1，CUDNN版本为7.6.5.32。

3.1.2 数据集构建

筛选、整理变压器图片并制作标签，构建变压器目标检测数据集。数据集包含不同类型、不同角度、不同环境下的变压器图片共489张，如图5所示。将数据集随机划分为训练集、验证集和测试集，训练集396张图片，验证集44张图片，测试集49张图片。在模型训练过程中，对训练集数据进行随机数据增强，包括缩放、长宽扭曲、翻转、色域扭曲等操作。

图5 变压器目标检测数据集中变压器图片

3.1.3 模型性能及检测结果

YOLOv4变压器目标检测模型的训练引入了迁移学习的理念，使用YOLOv4在ImageNet上的预训练权重帮助训练模型。模型共迭代训练100次，分为冻结训练和解冻训练2个阶段。在第1阶段的前50次迭代中，冻结预训练模型前249层的权重，设置一次训练所抓取的数据样本数量(batch_size)为2，初始学习率lr=0.001。当验证集loss连续3个迭代(epoch)不下降时，按lr减半自动减少学习率，当验证集loss连续10个迭代不下降时，提前停止这一阶段的训练。在第2阶段的后50次迭代中，对模型前249层权重进行解冻训练，设置batch_size为2，初始学习率为0.000 1，学习率下降及训练早停方法同第1阶段。YOLOv4模型在测试集上的类别平均精度(average precision，AP)曲线如图6所示。

图6 变压器测试集AP曲线

YOLOv4模型在测试集上的AP为99.77%，可见YOLOv4能准确实现变压器目标检测。对单张变压器图片的检测结果如图7所示，图中红色方框内的区域为检测出的ROI。

图7 YOLOv4模型单张图片检测结果

3.2 基于金字塔LK光流法和OTSU法的变压器振动检测

3.2.1 振动矢量检测结果与分析

本文首先采用人工合成的变压器振动视频作为测试数据，将变压器图像作为前景嵌入到背景图像中，并预先设定变压器在每帧中的位移矢量，与采用本文算法得出的位移矢量检测结果进行对比，以评估算法效果。振动检测算法运行环境为Windows10、64位操作系统，CPU型号为G4600，GPU型号为GTX1050，内存容量大小为8 GB，输入视频图像尺寸为666×666。

为减少干扰，本文未在整幅图像区域内计算特征点(如图8所示，特征点以绿色圆点表示)，而是通过YOLOv4模型检测变压器位置，并选取变压器中心的一块区域来计算特征点(如图9所示，特征点以绿色圆点表示)。在该区域内计算的特征点更能代表变压器本体，将其用于计算变压器振动矢量的结果更为准确。之后，使用金字塔LK稀疏光流法计算这些特征点在相邻2帧之间的振动位移矢量。然后，采用OTSU算法计算得到这些振动矢量的模的阈值，并滤除模值小于阈值的振动矢量以减少计算干扰。最后，计算所有剩余振动矢量的平均值作为变压器振动矢量的最终结果。

图8 整幅图像区域内的特征点

图9 变压器中心区域内的特征点

本文合成的视频尽可能还原了现实中变压器的振动模式。对变压器图像进行了来回摆动操作，同时也验证了不同振动幅度下的矢量计算结果，并与无目标检测方法计算出的振动矢量结果进行比较。部分测试数据记录见表1。

表1 人为设定的变压器振动矢量与采用本文方法以及无目标检测方法计算结果比较

由表1可见：本文方法计算得到的变压器振动矢量与人为设定的数据之间误差较小，精准度较高；将本文算法去除目标检测算法后，振动矢量的计算结果大幅偏离设定值。在实际环境中同样可以依据本文方法计算得到变压器振动矢量数据，从而对变压器的运行状况进行可靠性分析。除首帧以外，单帧处理时间约为11 ms，充分保障了算法的实时性。

为了进一步验证本文算法的准确性，引入归一化均方根误差(normalized root-mean-square error，NRMSE)、均方根误差(root mean square error，RMSE)、平均绝对误差(mean absolute error，MAE)、平均绝对百分比误差(mean absolute percentage error，MAPE)、方差变化百分比(percentage change in variance，PCV)来计算振动矢量误差率[20-21]。上述误差度量η(下标代表不同的误差类别)的定义分别如下：

(7)

(8)

(9)

(10)

(11)

表2 利用不同的误差度量验证本文算法的准确性

3.2.2 振动频率检测结果与分析

本节进一步计算特征点的振动频率。首先根据振动矢量计算特征点的二维坐标，计算完指定帧数之后，进一步将由各帧特征点坐标组成的数列进行快速傅里叶变换得到振动频谱。在滤除低频干扰后，取幅值最高的频率作为特征点的振动频率。图10(a)中，蓝色曲线代表随机选取的4个特征点的振动频率，可以看到本文方法计算出的变压器上不同特征点的振动频率值皆稳定在37.72 Hz，相较37.5 Hz的理论值差距很小；由此可见，本文方法计算出的频率随时间变化较为稳定，具备一定的抗干扰能力，且精度较高。图10(b)中，蓝色曲线是4个特征点依据合成视频预先设定好的数值计算出的理论频谱，红色曲线是经由本文方法计算出的频谱，可以看出红色频谱与蓝色的理论频谱重合度较高，证实了本文方法在频谱计算精度上有较好的表现。

图10 变压器4个特征点的频率随时间变化的曲线以及理论频谱与本文方法计算的频谱对比

图11所示为真实视频场景下的振动情况，图11(a)为真实视频中的振动音叉，图11(b)为真实视频中的振动钢板，各自的振动频率分别为280 Hz和440 Hz。其中绿色点为采用Shi-Tomasi方法计算得到的特征点。本文对音叉、钢板视频中随机选取4个特征点计算实时振动频率，并画出各特征点频率随时间变化的曲线及频谱图，如图12所示。图12(a)和(c)分别为本文方法计算出的音叉及钢板真实视频中随机选取的4个特征点的振动频率随时间变化的曲线。2个目标上的特征点振动频率分别稳定在279.46 Hz和439.12 Hz，与280 Hz和440 Hz的实际值差距很小。由图12(b)和(d)可以看到同视频中4个特征点的振动频谱较为一致，这表明本文方法在真实视频中同样具有很好的计算精度及抗干扰性能，保证了其实用性。

图11 真实振动视频中的特征点

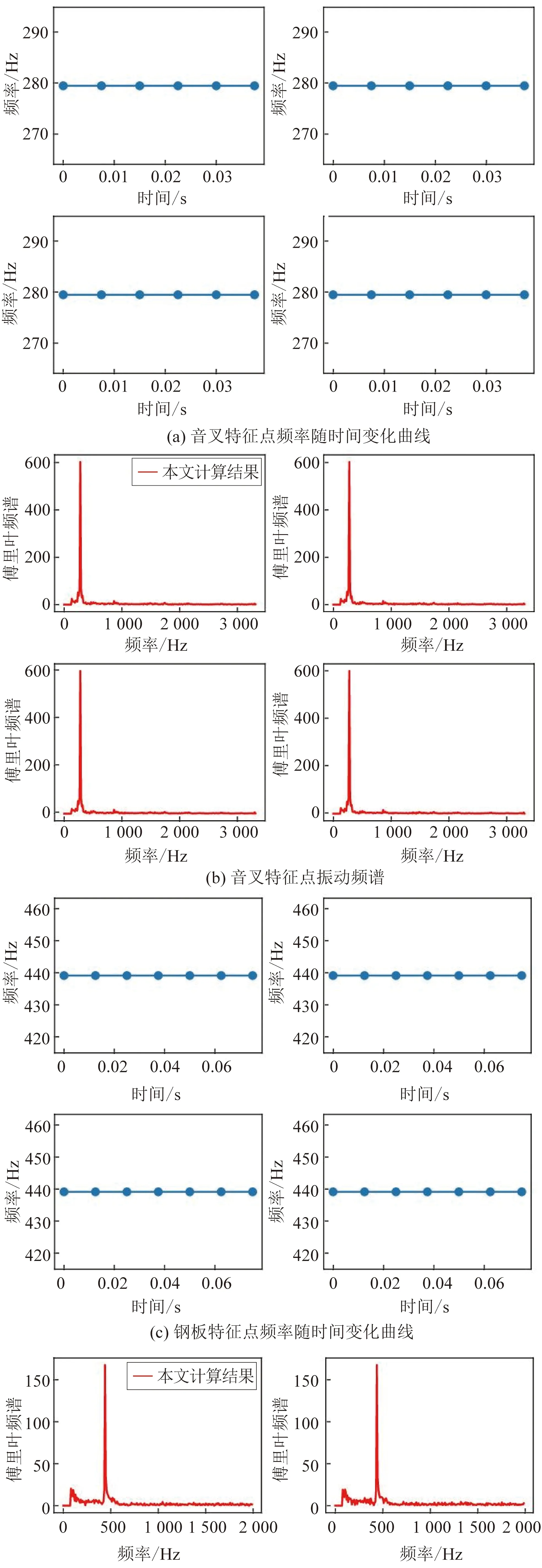
图12 各特征点频率随时间变化的曲线及频谱图

4 结束语

本文提出一种基于视频的变压器实时振动信号检测方法。首先通过YOLOv4模型以及迁移学习实现电力变压器的精确定位，然后在ROI范围内利用金字塔LK稀疏光流法计算得到特征点振动矢量，进一步利用OTSU算法滤除振动矢量干扰项，最后通过矢量平均计算得到变压器振动矢量。实验结果表明，在人工合成的变压器振动视频中，本文算法可以实时准确地计算变压器振动矢量及频率，为变压器的实时状态评估提供重要分析依据。