基于RBF神经网络的扑翼飞行机器人的姿态控制

牛廉政，何广平

(北方工业大学机械与材料工程学院，北京100144)

1 引言

自1992年美国首次提出微型扑翼飞行器这一概念，在过去的二十多年已取得迅速发展。鉴于扑翼飞行器可以低速飞行且能实现悬停的优点，所以可以在狭窄空间中灵活运动，从而完成各类飞行任务，而实现良好的姿态控制是完成精确定向、跟踪飞行任务的关键。

理论上，对于大多数鸟类而言，仅依靠调整尾翼转角，则可以产生力矩实现姿态控制。而大多数昆虫没有尾翼，则通过翅膀沿着几乎垂直的身体轴线高频拍动，以产生可以悬停的升力并通过调整机翼运动学来改变机翼所受气动力，从而实现对自身翻滚、俯仰和偏航的姿态控制。实际中，扑翼飞行器的姿态控制则面临着巨大挑战。一方面，由于扑翼飞行器质量小，易受到环境空气流动干扰，且自身呈现明显的非线性和非定常气动力特征。另一方面，因为扑翼飞行器尺度的原因，相应的传感器测量性能由于机翼拍动的影响也急剧下降，且在实际飞行中姿态角速度也很难获得实时反馈并得到精确测量。因此，设计的扑翼飞行器的姿态控制器应该具备较强的鲁棒性和适应性。而卡内基梅隆大学设计的飞行器首先采用解耦PID控制器进行了自由飞行可行性分析，但在研究过程中发现其对外界干扰的抵抗力不足。而基于反馈线性化的滑模控制要求系统模型是精确已知的，但是获取精确的参数信息在实际工程中是难以实现的。

在其它领域的姿态控制中，文献[11]针对水下航行器，基于RBF神经网络和积分滑模控制设计了鲁棒自适应控制器，证明了RBF神经网络的自适应性以及积分滑模的强鲁棒性。文献[12]研究了航天卫星的姿态跟踪控制问题，使用RBF网络摩擦补偿系统来近似估计在线切换项，实现了滑模控制律中的切换增益的平滑，从而减少了系统的振动。

借鉴上述研究经验，本文针对扑翼飞行器实际飞行中面临的气流干扰以及参数未知的问题，采用RBF神经网络逼近姿态动力学中未知项，设计自适应律减小神经网络逼近误差，引入改进鲁棒项使系统具有较强的鲁棒性，并有效解决了为克服干扰造成控制输入抖振问题。

2 姿态动力学模型的建立

本文以四扑翼飞行机器人(以下简称4-FMAV)为研究对象，如图1所示。其具有四个机翼组成X形主机翼和一个倒T型尾翼。主机翼仅用于产生升力和推力，未直接用于姿态控制，极大简化了控制策略。与主机翼相比，尾翼产生的空气动力学提供很小的升推力，主要用于FMAV的姿态调整。其中，4-FMAV左右2个水平尾翼同调转动产生俯仰力矩，差动产生滚转力矩，而偏航力矩则由垂直尾翼所决定。4-机体坐标系固定在本体上，其原点位于质心上。本体与轴对齐，轴指向4-的右侧。指向下方，垂直于平面，如图2所示。其中，二面角是机翼闭合时机翼与水平线所成角度。，，，分别代表左上翼，左下翼，右上翼，右下翼。

图1 虚拟样机示意图

图2 机体坐标系

目前常用的动力学建模方法是刚体的牛顿-欧拉法。其主要思想是根据刚体的运动方程，然后利用运动螺旋和力螺旋建立动力学方程。关于4-FMAV的动力学方程可以通过牛顿—欧拉方程表示为

(1)

考虑粘性力及外界干扰力矩，则4-FMAV的姿态动力学的状态空间方程形式为

(2)

3 姿态控制器的设计

定义期望的姿态角为∈，则姿态角误差∈

=-

(3)

设计关于误差的滑模面

(4)

其中，∈为滑模面系数，∈。()∈表示含有角速度未知项的非线性函数。

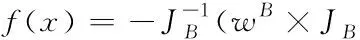
(5)

将式(5)带入式(2)，则包含未知项的姿态动力学模型可以进一步表示为

(6)

实际上，角速度信息很难测得准确值和得到及时反馈，可以采用RBF神经网络进行逼近。RBF神经网络能在一个紧凑集和任意精度下，逼近任何非线性函数。RBF的算法为

(7)

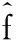
(8)

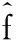
对式(4)求导得

(9)

为了使姿态角误差沿滑模面从任意状态渐进收敛于0，设计控制输入

(10)

其中，>0，此处双曲函数正切tanh()代替滑模控制中常用的sgn()，可有效避免控制输入抖振，如图7-9所示。

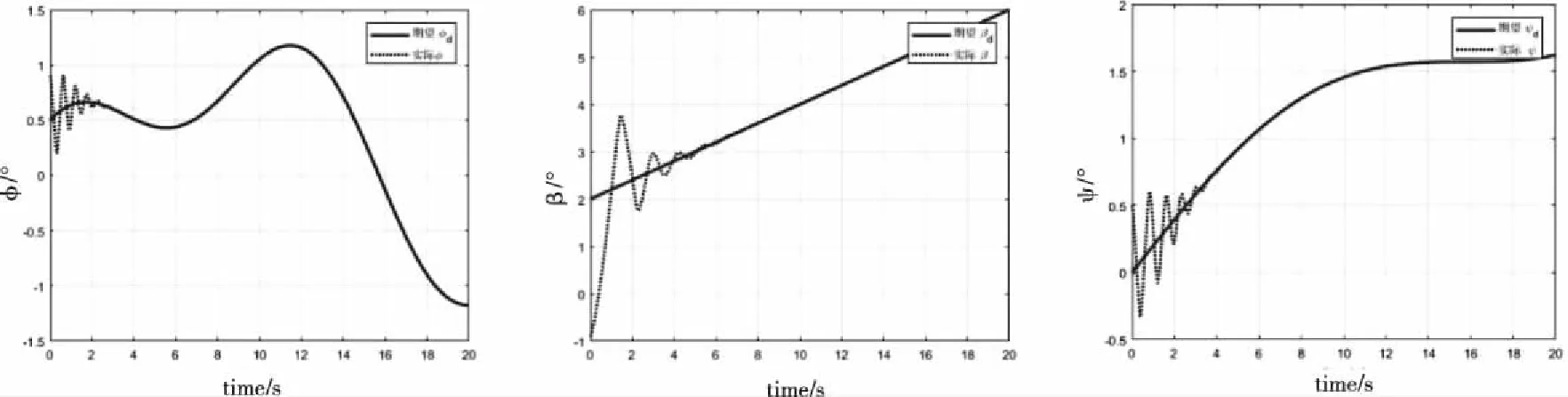
图3 俯仰角跟踪变化图图4 滚转角跟踪变化图 图5 偏航角跟踪变化图

图6 俯仰角速度跟踪变化图图7 滚转角速度跟踪变化图 图8 偏航角速度跟踪变化图

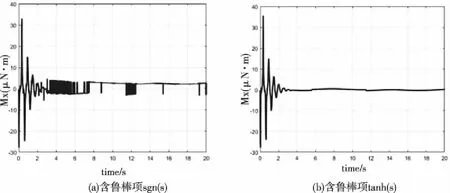
图9 俯仰输入力矩

图10 滚转输入力矩

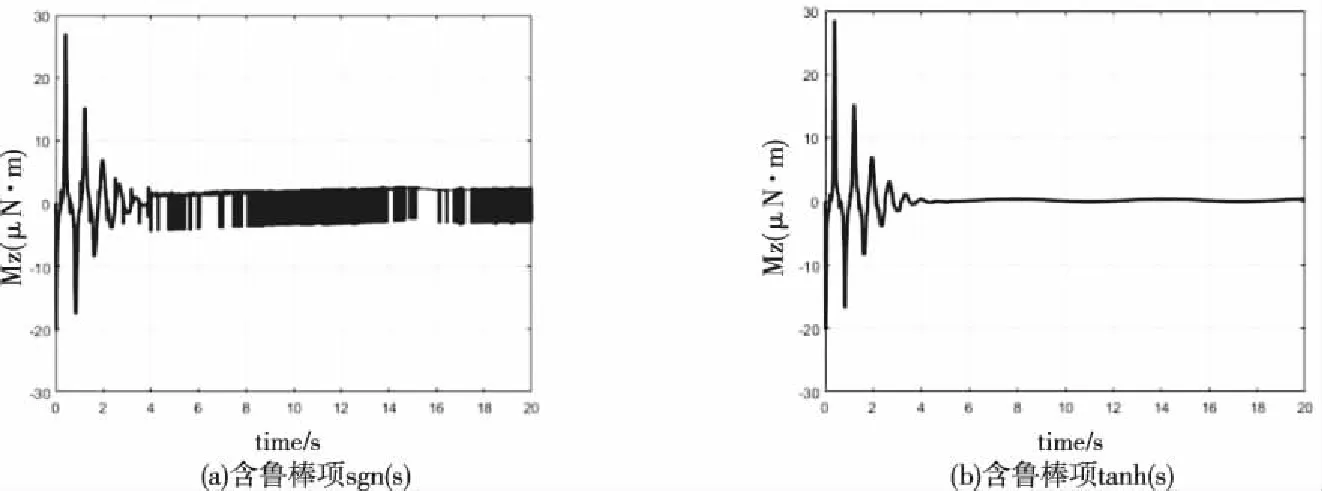
图11 偏航输入力矩

图12 RBF神经网络对‖f(x)‖的逼近 图13 逼近误差

将网络输出式(8)带入式(10)得到控制律：

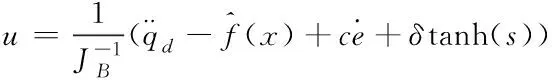
(11)

将控制律式(11)带入式(9)得

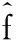
(12)

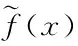
设计的滑模面∈是关于3个姿态角，则每个姿态角的Lyapunov函数为

(13)

对式(13)求导得：

(14)

=1，2，3。

设计自适应律为

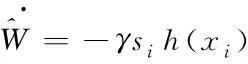
(15)

=1，2，3。

由于双曲函数()为值域属于[-1，1]的奇函数，则

=-(+)-||

(16)

=1，2，3。

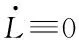
4 仿真结果及分析

为了验证设计控制器的有效性，制定了以下仿真任务：①姿态角及角速度跟踪效果；②对比2种鲁棒项姿态控制输入，是否有效解决控制输入抖振问题；③神经网络逼近效果。

根据图3-8姿态角和姿态角速度跟踪曲线可以看出，在有干扰的条件下跟踪效果良好，系统完成误差收敛时间短，且稳态误差小，说明基于滑模鲁棒自适应的RBF神经网络控制器具有良好的鲁棒性和适应性，能够良好的完成指定的姿态跟踪任务。

根据图9-11控制输入对比，在姿态跟踪、逼近误差相近的情况下，含有鲁棒项sgn(s)的姿态控制器由于克服干扰，造成了控制输入信号抖振，而含有鲁棒项tanh(s)的姿态控制器有效解决了控制输入抖振问题。说明设计的控制器在具有抗外界空气干扰力矩的同时，也有效的避免了控制输入存在的抖振现象，更加满足实际飞行需求。

根据图12-13，RBF神经网络对未知项()在6左右完成误差收敛，且稳态误差几乎为0，实现了对姿态动力学中未知项角速度项的良好逼近，解决了实际工程中模型参数项未知的问题。

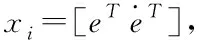
5 结论

针对扑翼飞行机器人姿态控制中面临的外界干扰及模型参数难以准确测量的问题。设计了RBF神经网络滑模鲁棒自适应控制器，采用RBF神经网路逼近姿态动力学模型的未知项，通过自适应律减少了神经网络逼近误差，改进鲁棒项克服了外界干扰并有效解决了控制输入抖振问题。这对工程实践中扑翼飞行器的姿态控制具有一定的借鉴意义。