基于FFD技术的飞翼布局无人机翼型优化研究

周 伟

(航空工业成都飞机工业(集团)有限责任公司，四川 成都 610092)

1 引言

飞翼布局是一种非常规的气动布局形式，其特点是机身与机翼高度融合，无明显分界面，且通常取消了平垂尾，整体外形犹如一个机翼。飞翼布局飞机因其高效的气动效能，低RCS特性等优势已成为飞行器发展的重要方向，从上世纪80年代开始，美国NASA、波音公司、欧洲空客公司、俄罗斯中央流体研究院等都开展了针对飞翼布局的研究项目，极大地推动了飞翼布局的发展。

飞翼布局采用无平尾设计使得控制舵面只能布置在翼身上，造成舵面力臂较短，纵向配平困难，这就要求飞翼布局飞机选用的翼型在设计点状态不能产生较大的俯仰力矩，否则将造成较大的配平阻力，降低气动性能。现代高亚音速以及跨音速飞机设计中，超临界翼型因其优异的跨音速阻力特性而得到广泛运用，超临界翼型外形通常在翼型后缘呈现一较大反弯形状，用以弥补因翼型上部存在较大平坦范围而引起的升力损失，后缘反弯将产生一较大低头力矩，不利于配平，因此对于飞翼布局飞机，在选用的超临界翼型基础上需根据性能要求进行更进一步的优化设计。

通常翼型优化设计流程主要包括三个模块，首先是参数化模块，通过对翼型外形进行参数化处理，施加扰动产生变形得到新翼型外形，其次是CFD(Computational Fluid Dynamics)仿真计算模块，根据新翼型外形自动生成流场网格并计算得到气动特性，最后是优化算法模块，运用优化算法对CFD计算结果进行寻优，判断是否达到优化目标，是则结束优化流程，否则继续循环此过程直到达到优化目标，优化流程如图1所示。

本文基于FFD(Free-form deformation)参数化技术对翼型上下翼面分别进行参数化，采用基于N-S方程的求解器计算翼型流场，采用NSGA-II (Non-dominated Sorting Genetic Algorithm II)多目标优化算法对计算结果寻优，建立了飞翼布局无人机高亚音速翼型多目标优化设计流程，优化结果达到优化设计目标。

图1 优化设计流程

2 优化设计过程

2.1 FFD参数化方法

外形参数化是气动优化设计的基础，通过参数化获取优化算法所必需的状态变量和约束变量等参数。FFD参数化方法由Sederberg和Parry于1986 年提出，其思想是仿照弹性体受外力后发生相应变形的物理现象，将研究对象(即待设计的几何外形)置于控制体框架内，给控制体施加外力，则控制体内的所有几何发生相应变形，处于其中的研究对象形状也随之发生变化。

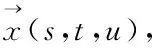
(1)

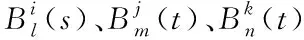
(2)

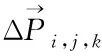
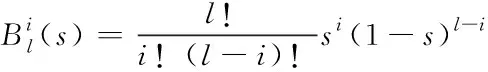
(3)

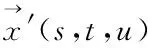
(4)

图2和图3给出FFD参数化技术的变形能力，蓝色虚线为所布置的FFD控制框，图2红色实线为初始翼型，通过控制1、2号控制点的位移，蓝色虚线控制框发生变形，从而改变了其中的翼型几何，翼型变形效果如图3所示，FFD方法具有连续性、凸包性、局部性、体积可控性等特性，不需要对初始外形进行拟合，变形能力强，在气动外形优化设计中适用性广。本文通过对上下翼面分别施加FFD控制框，并保持前后缘位置不变，上下翼面各有9个参数变量，实现了上下翼面能各自独立变形的参数化效果，且变量空间范围广。

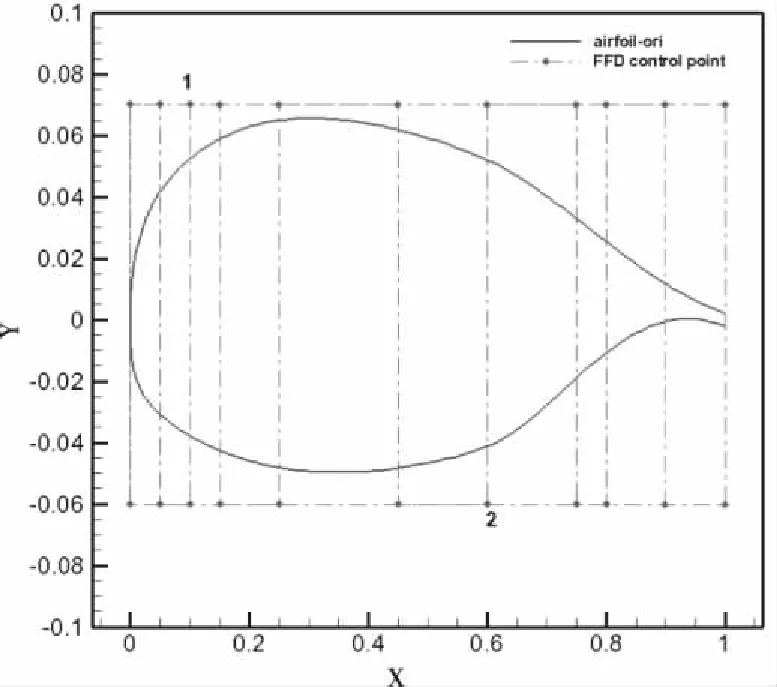
图2 FFD控制下翼型示意

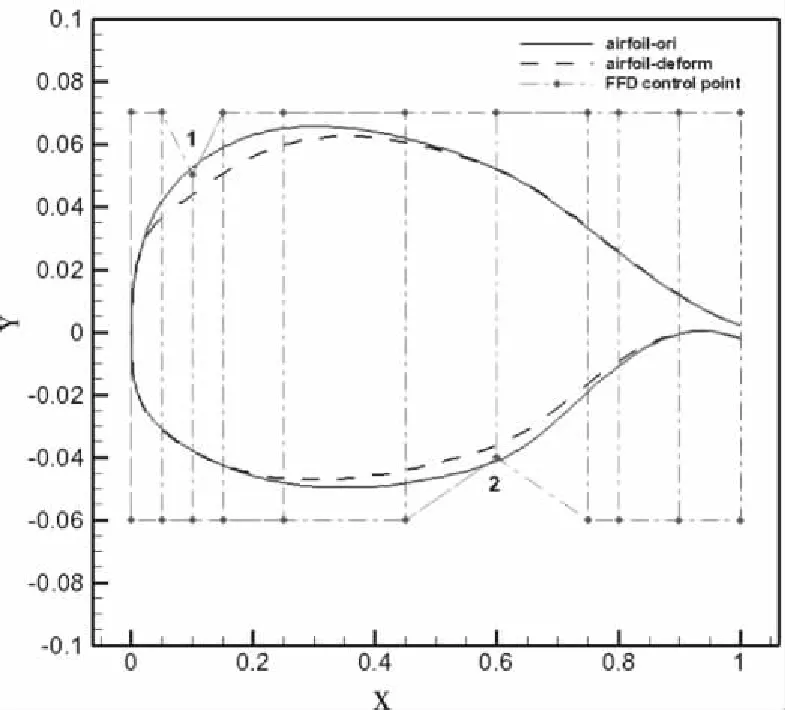
图3 FFD控制下翼型变形对比

2.2 流场计算

流场网格根据翼型几何形状，基于无限插值算法生成翼型结构化网格，网格数量601×109，第一层网格间距为5×10m，网格示意图如图4所示。

图4 网格示意图

流场求解采用了基于有限体积法思想和多块结构网格求解非定常雷诺平均N-S(URANS)方程的计算程序，选用SST湍流模型，三维积分守恒形式的N-S方程表述如式(2)所示

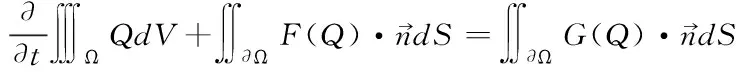
(5)

2.3 NSGA-II优化算法

NSGA-II是一种以非支配形式排序，采用精英目标策略并考虑了约束条件和样本拥挤距离的多目标遗传算法，是目前公认效果最好的多目标优化遗传算法之一。NSGA-II基本思想为：首先，随即产生规模为N的初始种群，非支配排序后通过遗传算法的选择、交叉、变异三个基本操作得到第一代子代种群；其次，从第二代开始，将父代种群和子代种群合并，进行快速非支配排序，同时对每个非支配层中的个体进行拥挤度计算，根据非支配关系和个体拥挤度选取合适个体组成新的父代种群；最后，根据遗传算法基本操作产生新的子代种群，以此类推，直到满足结束条件，NSGA-II算法具体流程如图5所示。

图5 NSGA-II算法流程图

3 结果分析

3.1 问题描述

公式(6)给出了二维翼型和三维机翼设计点间的关系，式中，下标2和3分别表示翼型和机翼，表示升力系数，为马赫数，14为机翼14弦线后掠角，为相对厚度。

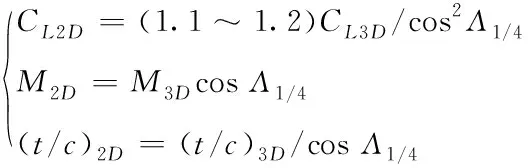
(6)

根据飞翼布局无人机的巡航设计条件，确定二维翼型的设计点为：巡航马赫数=065，巡航升力系数=039，单位尺度雷诺数=525×10，优化目标及约束表述如下

3.2 优化结果

本文案例的优化问题包含2个优化目标和1个约束目标，是典型的多目标加约束的优化设计问题，具有工程实践意义。首先，基于拉丁超立方均匀分布算法产生50个样本点构成初始化种群，再利用NSGA-II多目标遗传优化算法进行50代优化，获得了优化解的分布，如图7所示，由图可看出没有较明显的Pareto前沿，此时选取最终优化设计解容易陷入局部最优状态。阻力的收敛效果较明显，图7给出了阻力值随优化迭代步数的变化，由图可知，超过1500步后阻力值变化较小，呈收敛状态。

图6 阻力系数和俯仰力矩系数分布

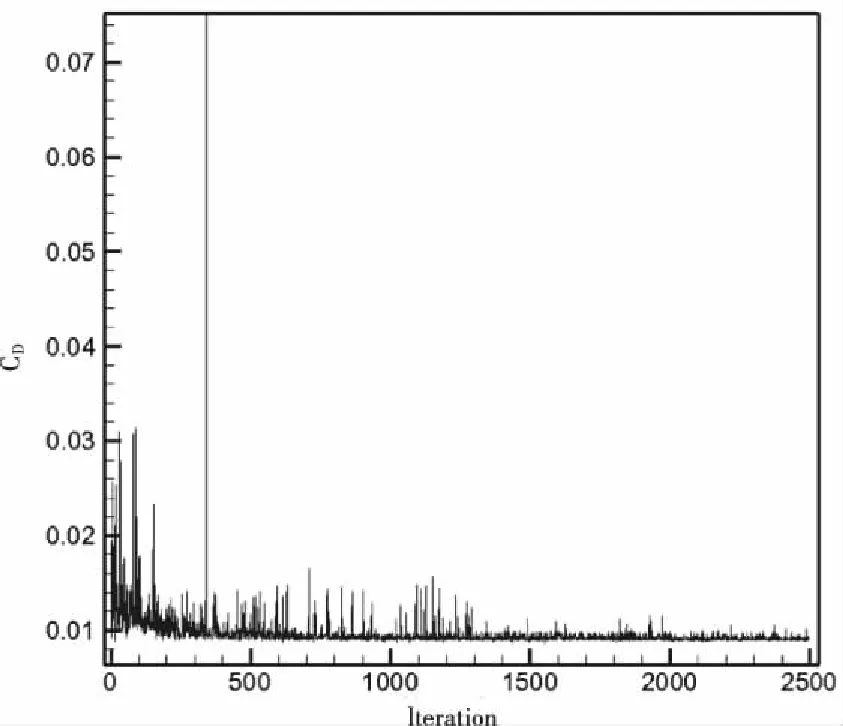
图7 阻力优化收敛过程

在本次优化基础上上，选取Pareto解集合作为初始化种群，利用NSGA-II遗传算法再进行50代优化求解，获得如图8的优化解分布，解的分布上呈现较明显的Pareto前沿，优化效果显著，从中选取了最终优化设计点(图中红框处)。优化前后翼型与初始翼型对比如图9所示，优化前后翼型压力分布如图10所示，其中Opt代表优化后翼型，Ori代表初始翼型，由图9看出，为达到优化目标，在满足最大厚度约束条件下，优化后翼型头部下表面前缘呈一较小弯度，以增加抬头力矩即降低低头力矩，后缘弯度减小，进一步降低翼型的低头力矩，翼型头部形状的改变，导致上翼面前缘吸力区范围扩大，达到减小阻力的效果，总的来说由于亚音速状态下翼型阻力以摩擦阻力占主导，通过阻力优化减小翼型型阻获得的收益不高。

图8 阻力系数和俯仰力矩系数分布

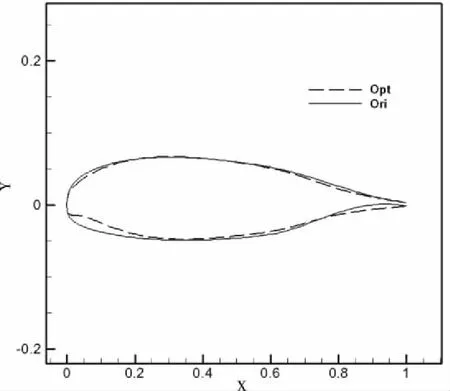
图9 优化前后翼型对比

图10 优化前后翼型表面压力分布

优化结果数据见表1，相比于初始翼型，优化翼型低头力矩大幅减小，阻力减小5.4%，升阻比提高5.7%，优化效果良好。

表1 优化结果

4 结论

本文基于FFD参数化方法结合NSGA-II遗传优化算法建立了飞翼布局飞机翼型多目标优化设计流程，实现了翼型高亚音速巡航状态下的优化设计目标，可得到如下结论：

1)通过建立的翼型多目标优化设计流程实现了多目标加约束的优化设计目标，优化效果良好，可广泛应用于工程实践中。

2)将基于初次优化的Pareto解集作为再次优化的初始种群可以获得更优的优化解分布，提升优化效果。