基于特征分解的短期电负荷组合预测模型研究
林 涛,赵 伊,冯嘉冀
(河北工业大学人工智能与数据科学学院,天津300000)
1 引言
人口增长和经济发展促使能源使用量大幅度增加,供电公司在满足用户日常需求的同时,为保证电量供给正常,还会提升20%的发电量用来满足可能发生的5%潜在高峰用电,用电供需不平衡造成了剩余电力的浪费,势必会对电力资源和生态环境造成影响。因此针对短期用电,可以通过准确预测用户的用电需求,从而做到精准供电,减少资源浪费。
现如今深度学习模型因具有更高的预测精度从而被广泛应用于最近的电力预测当中。文献[2]将循环神经网络模型(Recurrent Neural Network,RNN)运用到电负荷预测上,尽管在预测效果上有所提升,但对时序数据之间关联性的研究仍有欠缺。文献[3]使用的时间卷积网络捕获长期时序依赖关系的的能力胜过其它深度学习模型,被证明更适用于时序数据预测。单一类型的神经网络一般只擅长挖掘数据的某一类特征,而对于电力数据而言,影响耗电的因素不止是功率、电流、电压等,也与季节、天气、地理等特征有关,因此预测模型要具有挖掘数据多方面特征的能力。文献[5]提出一种基于LSTM和时间序列分析法相结合的组合算法用于短期风速的预测,实验证明LSTM在捕捉数据随机性和非线性特性表现良好。文献[6]提出了一种基于经验模态分解(Empirical Mode Decomposition,EMD)和LSTM相结合的负荷预测模型,将时间序列信号分解为数个本征模函数(Intrinsic Mode Function,IMF)分量和趋势分量,分别进行预测,结果表明相比于单一模型预测精度得到很大提升,但分解过程中产生了不可避免的误差问题。文献[7]使用聚类(Clustering Analysis,CA)、主成分分析(Principal Component Analysis,PCA),小波分解和重构技术获得合理的模型输入,用多层感知神经网络(Multi-layer perceptron neural networks,MLP neural networks)和支持向量回归(Support Vector Regression,SVR)建立预测模型,探究了不同模型输入选择方法对热负荷预测模型的影响,结果证明,经过小波分解和重构技术来优化输入数据在模型预测中取得最优效果。
通过对以往预测模型的研究,本文提出了一种基于特征分解的组合预测模型,首先全方位分析了影响电负荷变化因素,引入“影响因子”,使用WD技术将原始电力数据分解为多频段子序列,通过计算相关度系数筛选出相关度较高的子序列,计算残差并保留相关度系数;然后针对不同频段数据特点,分别使用带循环滑窗策略的TCN模型和LSTM模型进行预测;最后对预测结果按照相关度分权求和。实验使用住宅用电数据,从用户侧角度出发分析数据特征,实验结果证明了本文提出的基于特征分解的组合模型在短期预测中具有较高的准确性与泛化能力。
2 基于特征分解的组合预测模型
2.1 基于特征分解的WD算法
一般用电数据变化都具有趋势性,但存在某时用电急剧增加的情况,因此高峰时刻用电是必须考虑的因素;由于季节不同、地理位置的不同也会对用电量产生不同的影响;采集器故障、供电故障、正常检修等特殊情况也需要考虑其中;针对特殊用电情况发生,还需要考虑到事件的随机性。通过综合分析实际用电情况,影响电负荷变化的特征可以归纳为:趋势因子、高峰因子、季节因子、地理因子、故障因子、随机因子。
本文采用的小波分解方法是一种非平稳信号分析和处理的方法,将原始信号分解为高频信号和低频信号两部分。高频信号在短时间内变化剧烈,从波形上看表现为波长尖锐剧烈的变化;低频信号在短时间内变化平缓,从波形上表现为平滑的大波长变化。因此使用小波分解方法分解电力数据,分解后的信号适合用于表征影响电负荷变化的影响因子。
分解采用Symlets5小波基函数,过程如下:
1)初始信号被分解为高频信号和低频信号。
2)高频信号继续分解产生两个信号:一个是新的低频信号,另一个是高频信号。
3)进一步分解高频信号,直到获得一系列噪声干扰信号为止。如下方法
-1=′·+′·
(1)
其中,为低频信号,为高频信号。′为高通滤波器,′为低通滤波器。是在分辨率为2下的高频分量部分,是在分辨率为2下的低频分量部分。根据之前的分析,将电力数据中的有用功率分解得到时间序列分为 6 个子序列,过程如图1。

图1 小波分解过程
其中,高峰因子用高频信号表示,原因是高峰因子反应短时内用电的极端变化,从波形上看通常就是小波长尖变化;其余影响因子分别用低频信号表示,分别为:趋势因子、季节因子、地理因子、故障因子、随机因子;
2.2 基于循环滑窗策略的TCN预测模型
本文采用的时间卷积网络是一种能够处理时间序列数据的卷积神经网络。为了实现长期有效的历史大小,膨胀因果卷积可以通过选择更大的滤波器尺寸来增加TCN的接受域。但是当历史时间较长时,TCN会出现较大的误差积累,导致预测精度下降的问题。
针对上述TCN算法存在的问题,提出一种基于循环滑窗策略的TCN预测模型,通过不断调整滤波器尺寸,循环迭代预测,保证每次预测的精度,步骤如下:
1)设置滤波器初始尺寸m,预测长度为n=1;
2)设置TCN模型参数,将长度为l的训练集使用TCN模型迭代训练,根据损失函数MSE最小化,使用随机梯度下降法找到最优参数,如果迭代次数满足预设迭代参数,则得到最终TCN模型;
3)使用得到的TCN模型,对t+1时刻电负荷进行预测,保留预测值到pre[],并将预测值输入训练集末端,同时n+1;
4)当滤波器长度m>预测长度n,停止循环,预测结果为此时pre[]的值。否则将训练集向右滑动一个窗口,长度不变,重复(2-3)过程。
上述方法能保证每次预测结果的误差较小,同时预测精度较高。
2.3 基于特征分解的短期负荷组合预测模型
本文提出一种基于特征分解的短期电负荷组合预测模型(WD-CSTCN-LSTM)。通过WD方法将从单一数据中分解出多种特征和特征残差,针对不同特征使用不同的预测方法,流程图如图2。

图2 流程图
算法步骤如下:
1)数据预处理。对于原始电力数据预处理,包括对于缺失值差补,这里采用的是均值差补;,再使用高斯滤波去噪。
2)特征分解。分析影响用电数据的特征,对于用电使用WD方法分解为高频序列A和低频序列D,对于各序列采用相关度分析,去除无关特征或相关度低的特征,筛选能够表征影响因子的子序列,并保留相关度作为权值,将原始数据减去保留序列生成残差序列,将所有的子序列归一化处理。
3)组合模型。预测模型可以在小波分解处理的多个频带内建立,针对(2)得到的序列,根据数据变化特点,对高频序列和残差序列采用LSTM模型,对于低频序列采用CSTCN模型,将各频段和残差预测结果按照权值求和,得到最终的预测值。
该组合预测方法,能够最大程度的保证各频段子序列的预测精度,残差序列弥补了影响因子选择时未入选的序列带来的误差问题,按权求和保证了各影响因子影响能力的准确。从整体提升了预测精度,降低了误差。
3 实验及结果分析
3.1 数据集选取及划分
实验采用的数据集来自于巴黎一所住宅收集得包含2006年12月至2010年11月用电数据(本数据集由UCI机器学习库提供),每一分钟采集一条记录。
本实验随机选取一天用电数据,记录共1440条,作为短期电负荷预测的数据集,其中1205条记录作为训练数据集,235条记录用于测试数据集。训练结束后,又在工作日、休息日、第一季度、第二季度、第三季度、第四季度中各随机选取一天的记录采取相同训练集与测试集划分方式进行实验,测试模型的泛化能力。
3.2 评价指标
本文使用的评价指标为均方根误差(Root Mean Square Error,RMSE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)、绝对平均误差(Mean Absolute Error,MAE)、决定系数(R-square,R2),如下方法
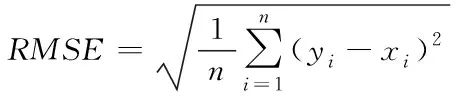
(2)

(3)

(4)
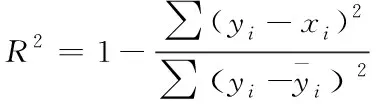
(5)
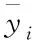
3.3 数据预处理
原始数据在刚获得时存在很多噪音,这主要由于采集方式和工作环境引起的。在数据进行实验前要对原始数据进行预处理,噪声处理使用高斯滤波方法,高斯滤波使用的高斯函数如下方法,滤波后降低了数据噪声并提高数据质量。
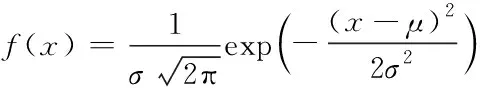
(6)
3.4 实验结果分析
3.4.1 特征分解实验
以一组日用电数据集为例测试模型性能,首先对分钟平均有功功率进行小波分解,得到10个子序列,分解结果如图3所示。
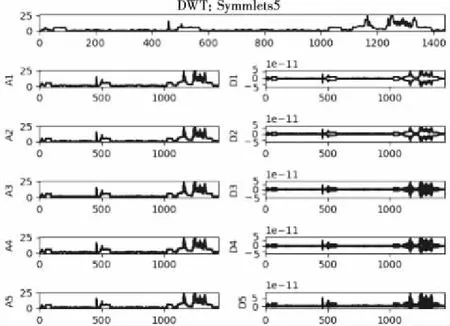
图3 小波分解后的子序列
考虑影响电力消耗的因素众多,使用皮尔逊(Person correlation coefficient)相关系数,来衡量特征值与预测值的相关度,皮尔逊相关系数计算如下方法
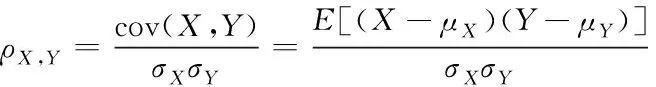
(7)
结果范围为-1到1之间,负值为负相关,正值为正相关,绝对值越接近1,相关度越高,相关度系数r与相关性的关系见表1。
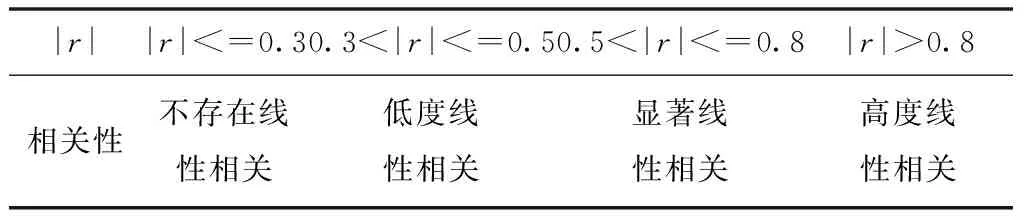
表1 相关度系数与相关度
表2是经过相关度筛选后的特征频段及其相关度系数,筛选的原则是去除不存在线性相关的频段,最终保留低频信号1~5和高频信号5,并计算残差序列。

表2 相关度系数
3.4.2 单一预测模型实验
将CSTCN与TCN,LSTM.ANN,GRU模型使用相同数据集进行实验,对比效果如图4

图4 单一模型对比图
通过图4和表3可以看出TCN模型善于捕捉时序数据整体变化趋势,拟合度较好,而CSTCN在预测精度上表现出较好的性能;LSTM在捕捉峰值上更为准确。根据各频段信号变化特点,得到以下结论:CSTCN适合预测低频信号,LSTM适合预测高频信号和残差序列。
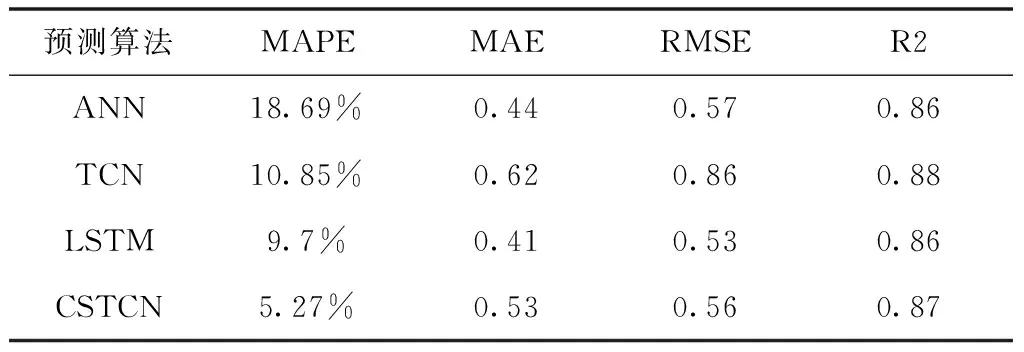
表3 单一模型预测结果
3.4.3 组合模型及其对比实验
经过特征分解后的子序列和残差序列分别使用CSTCN和LSTM模型得到的预测结果与真实值对比如图5所示。
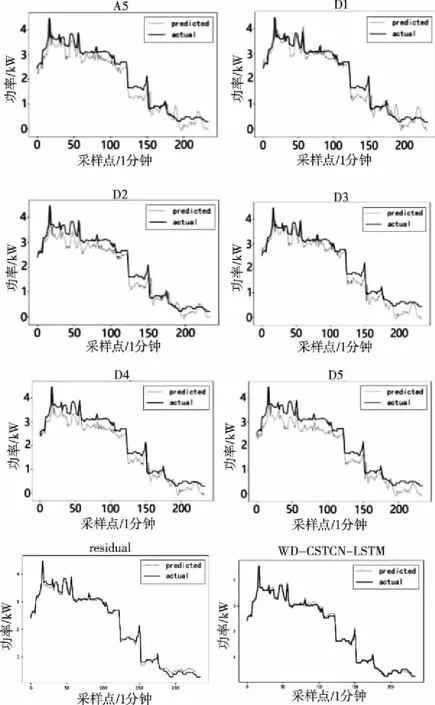
图5 预测结果对比图
使用3.2小节提出的评价指标进行分析,从分析结果可以看出:四项指标均得到了不同程度的提高。结果证明了组合多种预测模型能有效提高预测精度,降低误差。子序列预测结果与最终结果的评价指标结果见表4。

表4 评价指标结果
实验又对比了EMD分解方法和VMD下的预测模型,从表5和图6可以看出,三种方法拟合度均表现良好,而使用WD分解方法的模型在预测精度上明显高于其它方法,同时引入残差序列也能使误差降到最低。

表5 评价指标结果
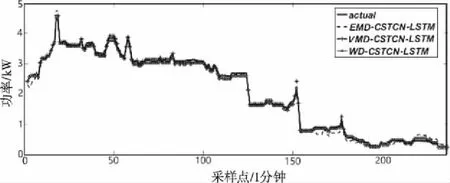
图6 不同分解方法对比图
4.3.4 不同典型日实验
仅根据某一天的数据不能证明模型的泛化能力,由于季度不同以及工作日和休息日的差别,电负荷会有较大变化,因此本文分别对工作日、休息日、第一季度、第二季度、第三季度和第四季度中随机选取的某一天进行相同实验,预测结果见表6所示。可以看出,面对不同的耗电量、高峰时段、用电趋势以及季节影响等因素影响下,本文提出的WD-CSTCN-LSTM模型的MAPE能稳定在3.86%以内,且小于对比算法中其它预测模型,从而证明了模型具有较高的泛化能力。
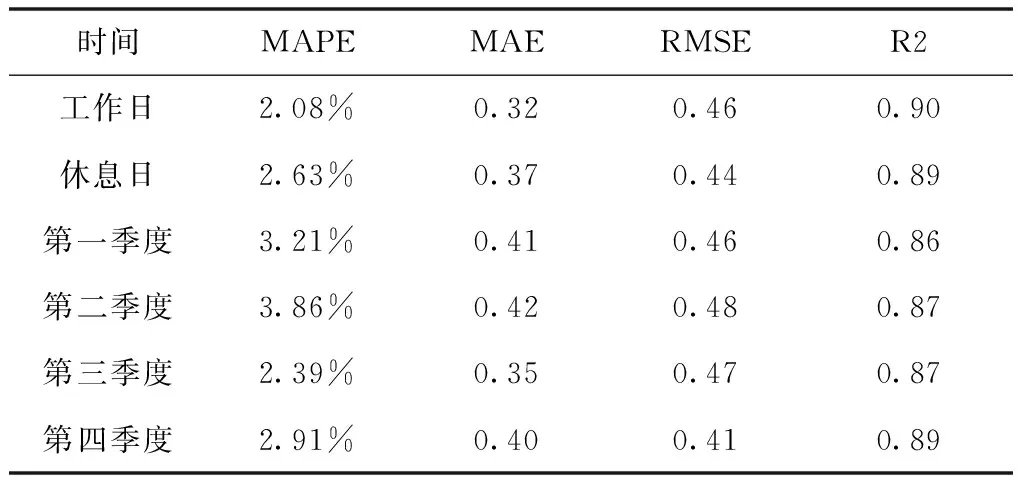
表6 评价指标结果
4 结语
本文立足于短期用户侧耗电预测领域,针对电力数据特征挖掘不全面的问题,提出了基于特征分解的短期电负荷组合预测模型。该模型深入挖掘了影响电负荷变化的特征后,通过小波分解手段使特征多样化,引入影响因子,如高峰因子、季节因子、地理因子等用来捕捉少量剧烈变化和季节以及地理环境造成的影响,将分解得到的特征经过相关度分析筛选,得到的子序列和生成的残差序列分别利用CSTCN和LSTM模型进行预测,预测结果按相关度系数分权求和最终得到组合预测值。实验结果表明了结合实际用电数据情况和电负荷预测影响因素的分析,针对不同影响因素使用不同的预测模型的方法能够有效提高预测精度,降低误差,更适用于短期电力预测的结论,同时对工作日、休息日、四个季度分别进行相同实验,实验结果证明了模型的泛化能力。然而,模型中使用的卷积网络在训练过程中花费时间较长,增加了训练时间,这一问题将应该是下一步的需要考虑的重点。

