中考数学几何复习策略分析

许晓娟

(广东省广州市增城区应元学校,511300)

初中几何既是教师教学的一大难点,也是学生学习的一大难点.弄清几何难的原由、研究几何复习策略，对于攻克“几何难学、几何难教”意义重大.

一、初中几何难点剖析

1. 辅助线的添加缺乏经验

几何题通常需要通过添加辅助线达到完善图形,以凸显图形中线段、角之间关系的目的.但学生缺乏基本图形的识别以及成功添加相应辅助线的经验.

案例1(2020年天津中考题)如图1,ABCD的顶点C在等边∆BEF的边BF上,点E在AB的延长线上,G为DE的中点,连结CG.若AD=3,AB=CF=2,则CG的长为______.

不少同学对此题中的条件“G为DE的中点”无从下手,甚至有部分同学连结了DF后,试图证出DF垂直于GC的延长线,学生有了添加辅助线的意识,但缺乏添加辅助线的方法与技巧.

解法1构造倍长中线解决问题

解法2构造中位线解决问题

案例2(2020年河南中考题)如图2,在边长为的正方形ABCD中,点E,F分别是边AB,BC的中点,连结EC,FD,点G,H分别是EC,FD的中点,连结GH,则GH的长度为______.

当几何图形中出现“双中点”条件时,构造中位线往往是首选的辅助线作法．

解如图3,连结CH并延长交AD于点T,连结ET.

易证∆TDH≌∆CFH,所以CH=TH,

反思辅助线添加的有效性教学依赖于教师在讲解中讲清辅助线添加的缘由,如案例2中遇中点、遇双中点常见的几种辅助线添加方法的总结,而不是单纯地讲解法,及时总结辅助线添加经验,可以让学生感受到辅助线添加有迹可循,降低学生对添加辅助线的恐惧感.

2.三类语言的转换存在障碍

初中数学的三类语言分别为符号语言、图形语言和文字语言.符号语言是一种由数学符号、数学术语和经过改造的自然语言组成的科学语言,具有确定性强、通用性高、简洁明晰等特点[1].但与此同时,符号语言也具有较强的抽象性,这是几何题成为难题的重要原因.图形语言是几何题中的直观图形表示,与符号语言的抽象性不同,图形语言具体而直观,但却需要学生具有较强的图形处理能力[2].三种语言的转换既需要教师在定理新授课中有意识地设计图形语言、文字语言、符号语言相互转换环节,又需要学生在解题中多次规范书写训练,才能达到自然转换的效果.

二、中考几何复习策略分析

1.重视常见几何模型的渗透应用

初中常见的几何模型如半角模型、手拉手模型、一线三垂直模型、对角互补模型等等,当学生掌握了这些模型的条件与结论,并能独立证明这些结论后,学生在复杂图形中能够快速发现模型中的基本图形,运用这些模型相应的分析思路,便能够在短时间内找到解决几何题的突破口.

案例3(2021越秀一模改编)如图3,在四边形ABCD中,∠A=∠ADC=90°,AB=AD=10,CD=15,点E,F分别为线段AB,CD上的动点,连结EF,过点D作DG⊥直线EF,垂足为G.点E从点B向点A以每秒2个单位的速度运动,同时点F从点D向点C以每秒3个单位的速度运动,当点E运动到点A时,E,F同时停止运动,设点E的运动时间为t秒.当GE=GD时,求AE的长.

若是能够抓住DG⊥直线EF,或GE=GD两个几何关系进行思考,可以想到“遇垂直构造一线三垂直”以及“遇等边共顶点构造旋转”.下面对两种模型进行解析.

依题意得,BE=2t,AE=10-2t，DF=3t.

解法1构造一线三垂直模型

如图3,过点G作PQ⊥AB于点P,PQ⊥CD于点Q,设EP=x,易证∆GEP≌∆DGQ,∆EPG∽∆GQF,x=t.

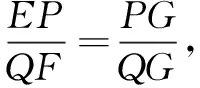
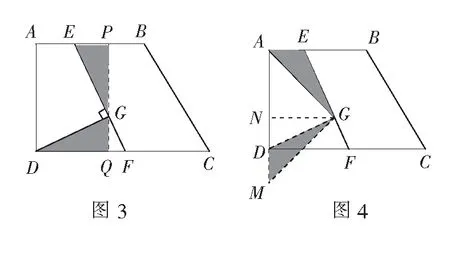
解法2等边共顶点构造旋转

如图4,连结AG,将∆EGA绕着点G逆时针旋转90°得到∆DGM,易证点A，D，M三点共线.

过点G作GN⊥AD于点N,

易证∆DGN∽∆FDG.

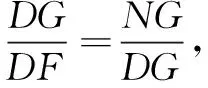
所以DG2=3t(10-t).

在Rt∆DGN中,DG2=t2+(10-t)2,

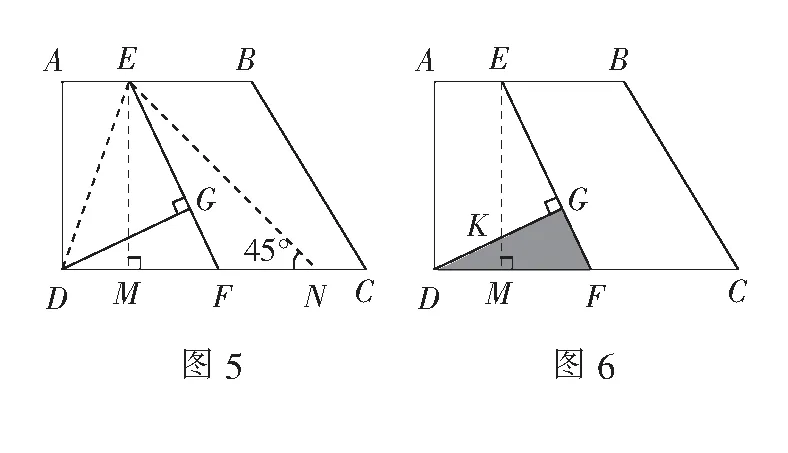
反思此题也可以连结DE,得到∠DEG=45°,遇45°构造共边共角型相似也能解答,如图5,∆DEF∽∆DNE;此题还可以根据等边GE=GD,构造一组全等的直角三角形,如图6,∆DGF≌∆EGK;从以上解题思路我们发现,通过图中一些几何特征联想到相关模型,添加辅助线构造该模型的基本图形,进而利用全等、相似或勾股定理得到变量间的数量关系是解决复杂图形的基本套路.

2.重视一题多解的合理应用

在中考二轮复习中,应避免题海战术,用好经典例题比无方向无重点的题海战术更有效益.选好题,用好题,防止单纯的就题论题,重点放在揭示思维过程上,引导学生多问几个为什么,力争从多个角度切入解题,通过一题多解巩固学生的解题能力,提高学生解题反应灵敏度,并重视题后反思,最后达到在短时间内提升备考效益的目的.

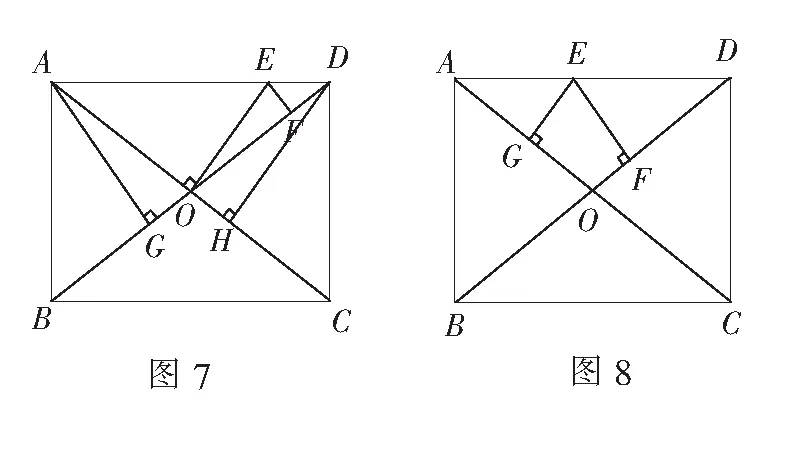
案例4(2020年广州中考题)如图7,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为( )

解法1由于本题中点E，F为定点,矩形也是确定的,经过测试,大多数学生第一反应会选择硬算出OE与EF的具体长度来得出答案通过设DE=x,利用线段数量关系或三角形相似表示出其余边,根据勾股定理列等式求解出x,最后完成求解可以看出学生解题经验不足,题中给出OE+EF应首选整体求值.

解法2在矩形ABCD中,

所以S∆AOD=S∆AOE+S∆DOE

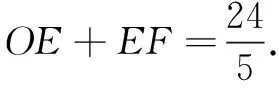
解法3由已知得,OE=AE·sin∠OAE,EF=DE·sin∠EDF.

在矩形ABCD中,AC=10,OA=OD,所以∠OAE=∠EDF.

OE+EF=(AE+DE)·sin∠OAE

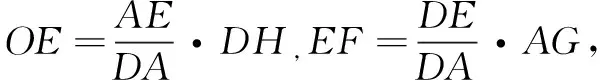
3.重视一般性几何结论的拓展证明

4.重视一类问题的解决策略研究

中考复习是一次系统梳理知识的过程,不是逐个知识点的重现与巩固尤其是中考二轮复习主要为专题复习,应以横向为主,对相关知识进行梳理、归纳、糅合,及时总结一类问题的解题策略.

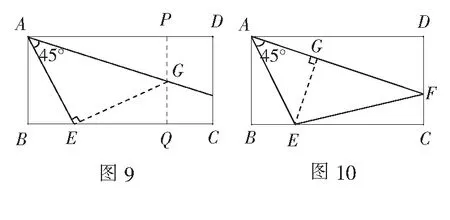
解法1遇45°作高构造等腰直角三角形

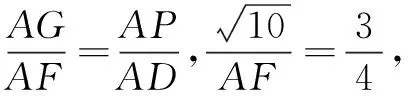
解法2遇45°作正方形构造半角模型

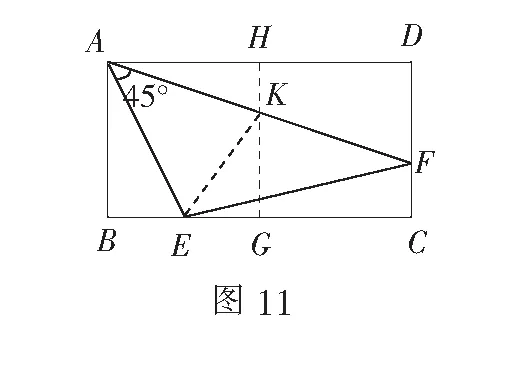
如图11,在线段BC上取点G,使得BG=BA=2,构造正方形ABGH,则点H恰好在线段AD上,GH交AF于点K.

由正方形中半角模型结论可知,BE+HK=EK(此处证明忽略).

设HK=x则EK=1+x，GK=2-x,EG=2-1=1.

四、 结束语

几何教学的三个关键词可概括为作图、思路、逻辑.几何教学应从学生最初接触几何图形开始,有目的地训练学生的作图能力,通过一题多解、多解归一训练学生几何问题解决的发散性思维.最后通过反思某一类问题的常见解决策略提高学生的逻辑推理能力,及时渗透几何模型,积累解题经验,并辅助以信息技术演示,提高学生的直观想象能力,从而达到教会学生研究几何图形的基本思路和探究数学问题的基本方法的目标.