变中找不变,立体不再难

◎刘得柱

(唐山市第二中学,河北 唐山 063000)

从最近几年的考题变化来看，以简单几何体为载体的线面位置关系的论证、角与距离的探求是常考常新的热门话题我们如何突破立体几何中的运动变化问题呢？下面本文从三方面加以说明

1 角度一：射影问题

在运动变化过程中，找容易度量的量

1(2018·新课标Ⅰ)已知正方体的棱长为1，每条棱所在直线与平面所成的角都相等，则截此正方体所得截面面积的最大值为(A)

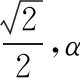
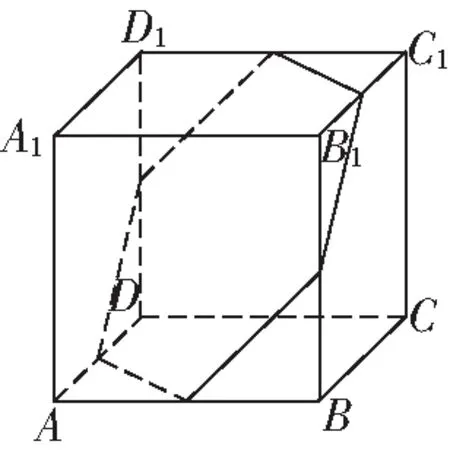
图1

我们如何判断此时截面的面积最大呢？一个很好的方法就是看截面在底面的投影的面积什么时候最大

图2中(1)与(2)投影面的面积比较，就是图3中△与四边形′′的面积比较

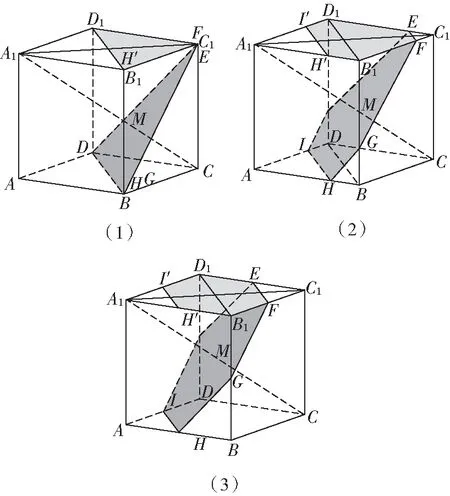
图2

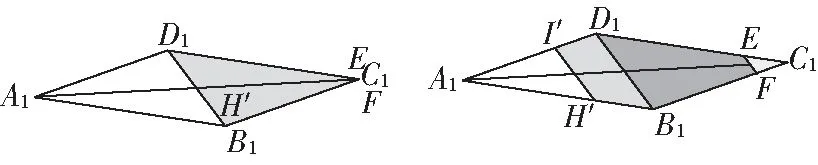
图3 比较(1)与(2)的底面投影

图2中(2)与(3)投影面的面积比较可以用同样的方法，如图4

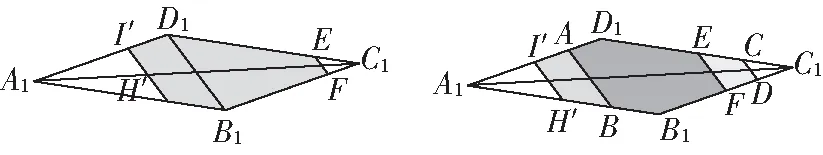
图4 比较图(2)与图(3)的底面投影

这种方法很重要的一个依据就是，变化过程的对称性以及变化过程中平面与底面所成的角不变，两底面间的距离不变，所以投影面的形状宽度不变，从而容易判断面积的大小

2(2020·海淀区期中)如图5，棱长为6的正方体的一个顶点在平面内

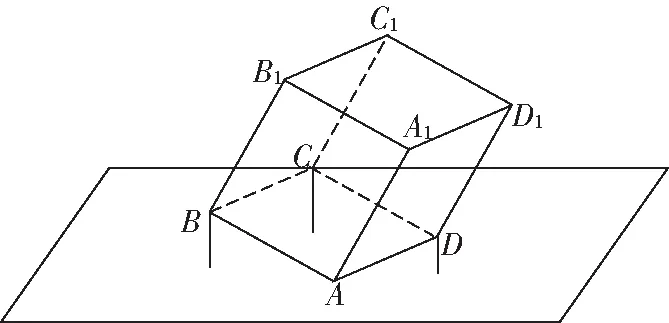
图5

(1)若正方体上与顶点共面的三个顶点、、到的距离最大值为3，且对应点为，是正方体的其余四个顶点中的一个，则到平面距离可能是(填写出所有正确结论序号)

①3 ②4 ③5 ④6 ⑤7

(1)为了求出各个顶点到平面的距离，我们要注意利用中点的纽带作用

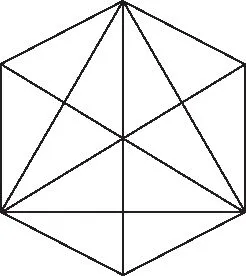
图6

这道题与正方体在太阳光下的投影(如图7)，有异曲同工之妙

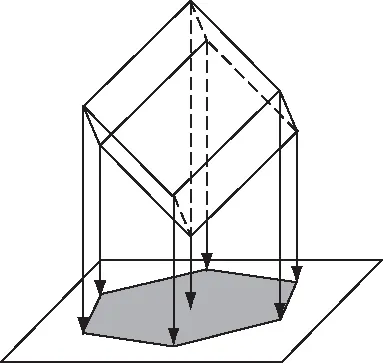
图7

A.(-2，6) B.(-6，2)

C.(-2，4) D.(-4，6)

本题可看作平面中的投影问题

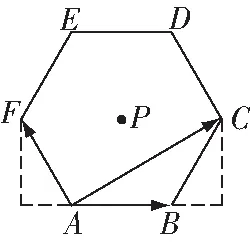
图8

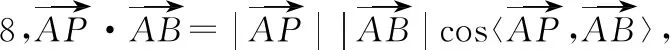
2 角度二：折叠问题

在运动变化过程中，找没有发生变化的量，如角度、长度等

4(2019·新课标Ⅲ)图9是由矩形、Rt△和菱形组成的一个平面图形，其中=1，==2，∠=60°将其沿，折起使得与重合，连接，如图10

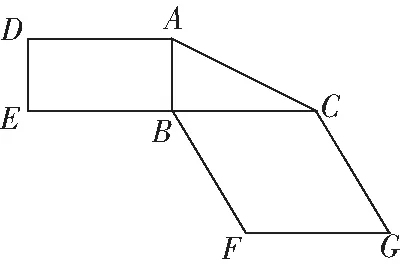
图9

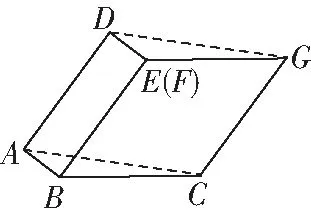
图10

(1)证明：图10中的、、、四点共面，且平面⊥平面；

(2)求图10中的二面角--的大小

(1)推导出∥，∥，从而∥，由此能证明、、、四点共面，推导出⊥，⊥，⊥面，由此能证明平面⊥平面

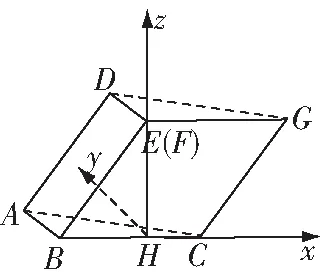
图11

本题要注意折叠前===2，⊥，⊥，而折叠后这些信息都没有变，这些条件正好是我们证明线面垂直和建立坐标系的依据虽然图形由二维到三维，发生了很大的变化，但不变的量是我们解题的依据

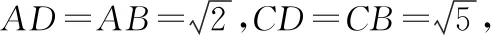
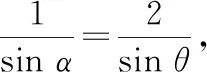
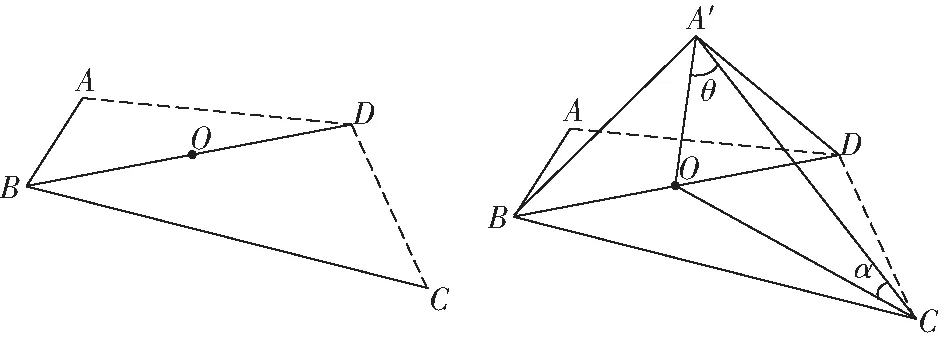
图12

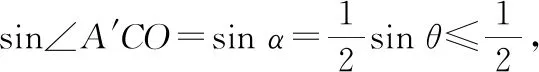
本题要注意折叠前后′与的长度不变，它们与的垂直关系不变，这是解题的依据还有就是角度的转化，由角转为角，角的变化比较明显(由0°到180°)，很容易观察

3 角度三：“动态”问题

在运动变化过程中，找高维度的量

点动成线，线动成面，面动成体，这是很简单的道理，运用到立体几何中却很有效点动的问题看线，线动的问题找面，面动的问题找体

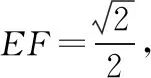
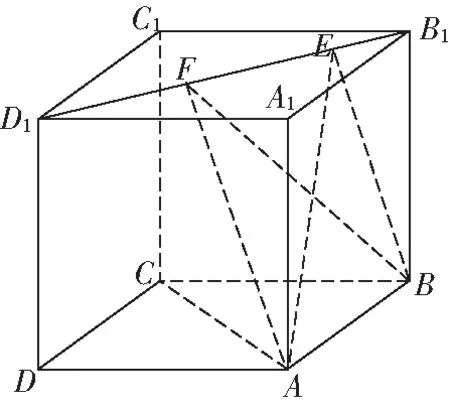
图13

①∥平面

②△的面积与△的面积相等

③平面⊥平面

④三棱锥-的体积为定值

②点到的距离大于，∴△的面积与△的面积不相等

③随着、两点的移动，、扫过的区域就是对角面，虽然△的形状在变，但它总在对角面内在正方体-中，⊥，⊥，∴⊥面，又面与面是同一面，⊂面，∴平面⊥平面

④要注意选择恰当的底面，以面作为三棱锥的底面，点到对角面的距离就是三棱锥的高∵△的面积为定值，三棱锥-的高即线段的一半，也是定值，∴三棱锥-的体积是一个定值

从近几年高考题目来看，试题注重能力考查，而运动变化问题注重创新，加强了试题的开放性、探究性，体现了数学探究的精神，是近几年高考命题的一个新热点对于此类问题，我们只需多想一步：“点动之后会怎样，线动之后会怎样？”在更广阔的视野中去观察、考虑问题，可能会有事半功倍的效果