两种分布曲线快速选型法在水文极值分析中的应用

任赵飞，王科华，张 军，李伟仪

（中交第四航务工程勘察设计院有限公司，广东广州 510290)

引言

目前，水文极值分析中常采用适线法[1-2]进行概率分布的选型和极值的拟合计算，这种方法优点在于比较灵活的考虑多种因素对分布曲线的影响，缺点在于人的主观任意性较强，不同的人即使采用同一种分布函数，得出的结果差异也可能较大。2015 年，孟彩侠等[3]分析比较了excel、频率计算软件和集对分析三种拟合方法的优缺点，认为集对分析法在一定程度上克服了常规目估适线法的主观任意性。随着商业软件的广泛应用，基于R 软件[4]、MIKE 软件等进行的水文频率计算和适线绘制极大的提高了工作效率，但他们也是基于目估的适线法。杜懿等[5]应用K-S 检验和A-D 检验分析6 种分布理论函数在降雨极值分析中的优劣。倪世伟等[6]提出基于Cs和Ck相对关系进行径流量分布函数的初步选型，但仅涉及4 种分布函数。

本文结合菲律宾马尼拉湾某项目极值风速设计，在对比国内外规范的基础上，分别采用两种理论分布快速选型方法选出的理论分布进行极值风速拟合，并对所得结果进行分析对比。所得成果可为类似工程设计提供参考。

1 K-S 检验和A-D 检验

K-S和A-D是两种统计学中常用的拟合优度检验方法，主要用来检验给定样本是否服从指定的分布函数，属于非参数检验方法[5]。

K-S 检验是以两位苏联数学家Kolmogorov 和Smirnov[6]的名字命名的，它是一个拟合优度检验。K-S 检验通过对两个分布之间的差异的分析，判断样本的观察结果是否来自制定分布的总体。A-D（Anderson-Darling）检验是对K-S 检验的一种修正[5]，相比K-S 检验它加重了对尾部数据的考量，K-S 检验具有分布无关性，它的临界值并不依赖被测的特定分布，而A-D 检验使用特定分布去计算临界值，这使得A-D 检验具有更灵敏的优势。

其中，K-S和A-D检验的统计量定义分别如下：

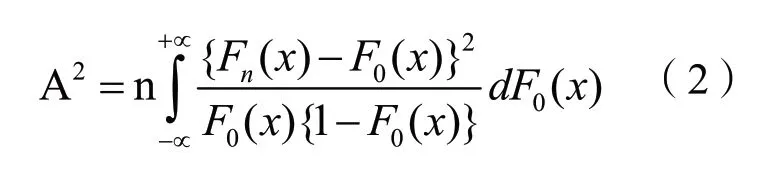
其中：D为K-S 检验的统计量；A2为A-D 检验的统计量；n为样本序列的长度；Fn(x)表示指定样本序列的经验分布；F0(x) 表示指定样本序列的理论分布。统计量值越小，说明指定分布函数的拟合效果越好，表现越优。详细计算原理与步骤见文献[7]。

2 偏度系数Cs和峰度系数Ck

2.1 Cs/Ck的统计学含义

偏度系数Cs主要用于反映样本概率密度曲线的对称特征[1]，即衡量样本在均值两侧分布的对称程度的参数。水文现象大多属于正偏，Cs>0。峰度系数Ck主要用于反映样本概率密度曲线在众数附近的“峰”的尖峭程度，正态分布的Ck=0。样本偏度系数Cs和峰度系数Ck的计算式如下：

式中：n为样本数；为样本均值，σ为样本方差。

2.2 不同理论分布函数的Cs和Ck

水文分布函数的Cs和Ck汇总如表1。

表1 不同理论分布函数的Cs和Ck

采用Matlab 编程，将上文提及的频率分布函数的Cs和Ck相对关系集中显示对比，如图1 所示。

图1 Cs和Ck相对关系

概率分布初步选型的主要步骤为：首先，根据表1 公式计算并绘制不同分布函数的Cs～Ck相对关系曲线；然后计算选取样本的Cs与Ck值，并将其绘制到上述Cs～Ck曲线中；最后选择与样本点距离最近的理论分布作为初步推荐的概率分布。上述方法的核心原理在于，当样本的Cs～Ck点越靠近理论分布的Cs～Ck曲线或点，则该理论分布越能较好的拟合出样本的对称性和扁平度。

3 实例应用

3.1 基本资料

以菲律宾马尼拉湾某项目为例。采用近海NOAA 1979～2016 年共37 年风后报数据为基础风场数据，如图2 所示。

图2 菲律宾马尼拉湾近海风速时间过程

由于工程区域受台风影响明显，台风期NOAA风的后报数据极值风速偏低，选取1977～2015 年工程位置200 km范围内的35场典型台风，采用Young&Sobey 台风场模型，利用JTWC 台风资料（其中包括时间、路径、台风中心最大风速和台风中心气压等）生成局部大范围海域台风典型风场，其中1995 年台风ANGELA 典型风场见图3。

图3 台风ANGELA 典型风场(1995.11)

以NOAA 后报风数据和JTWC 台风场数据为基础，共同合成工程位置37 年风数据时间序列。合成过程中采用典型台风风场模拟数据替换同期NOAA 后报风数据。

3.2 国内外规范对极值风速理论分布曲线的规定

关于极值风速统计分析所采用的理论分布，中国规范《海堤工程设计规范》[9]（GB/T 51015-2014）和《建筑结构荷载规范》[10]（GB 50009-2012）推荐采用极值I型，美国海岸工程手册[11]（CEM）推荐采用FT-I、FT-II 和威布尔（Weibull）分布，中国规范《港口与航道水文规范》[12]（JTS 145-2015）、英国规范（BS 6349）[13]、西班牙规范（ROM 0.4-95）提供了多种理论分布，并表明要以拟合最佳为原则选配。各国标准中，英国规范（BS 6349）明确指出极值统计分析中要确定外推值的置信区间，并明确数据样本必须确保各自相互独立，一场风暴最多只能选择一个样本参与极值统计。

总体而言，理论分布的选取，应以拟合最佳为原则进行选配，同时要确定外推值的置信区间。下文将基于2种样本筛选方法得到的典型样本进行理论分布的快速选型。

3.3 基于典型样本的理论分布快速选型

分别采用年极值法（Annual Maximum Method）和阈值法（Peak Over Threshold Method）从37 年合成风速时间序列中筛选出不分方向的极值风速样本系列。

1）利用Cs～Ck相对关系进行理论分布快速选型

分别计算年极值法样本和阈值法样本的偏度系数Cs和峰度系数Ck，并结合图1 中不同分布的Cs和Ck，见图4。

图4 两类样本和不同理论分布的Cs和Ck关系曲线

从图4 可以直观看出，对于筛选的样本，年极值法样本系列Cs～Ck点与G-Pareto 和Weibull 理论分布的Cs～Ck曲线相对更近，阈值法样本系列Cs～Ck点与G-Pareto、Pearson-III 和Weibull 理论分布的Cs～Ck曲线相对更近。

2）利用K-S 检验和A-D 检验进行理论分布快速选型

当K-S/A-D 检验的统计量小于对应于显著性水平ɑ=0.05 时的临界值（Critical Value）时，认为样本来自具有理论分布的总体，即符合理论分布，反之亦然。

从表2 可以看出，年极值法序列检验中，G-Pareto 和Pearson-III 均表现良好，Frechet 表现稍差，但均满足显著性水平；阈值法序列检验中，Weibull 表现最好，其次G-Pareto 和Frechet 表现稍差，但也均满足显著性水平。Gumbel、指数分布以及瑞利分布在K-S 检验/A-D 检验中均表现较差，选取的样本不满足相应频率分布的显著性检验水平。Log-Normal 分布对于年极值法序列，K-S/A-D检验均良好，满足显著性水平，但对阈值法序列的检验较差，不满足显著性水平。

表2 两类样本点的K-S 和A-D 检验结果

3.4 理论值

基于3.3 节初步结论，对于年极值法样本系列，本案例采用G-Pareto、Pearson-III、Frechet 以及Weibull 理论分布进行适线拟合，对于阈值法样本系列，采用Weibull 和G-Pareto 理论分布进行拟合，并给出95 %置信度的限值。

3.5 结果分析

分布的选择上，从3.3 节初步对比：

1）两种方法优选推荐的理论分布函数基本一致，即年极值法序列推荐G-Pareto 和Pearson-III 理论分布；阈值法序列推荐Weibull 和G-Pareto 理论分布。

2）两类样本的基于Frechet 分布的K-S/A-D 检验均满足显著性水平，而样本的Cs～Ck分布点却距离Frechet 理论分布Cs～Ck曲线较远。

3）阈值法样本Cs～Ck分布点距Pearson-III 理论分布Cs～Ck曲线较近，A-D 检验也满足显著性水平，但K-S 检验的统计量略大于临界值。总体而言，两类方法各有其特点，实际应用中建议结合使用，双向验证，从而选出最适宜所选样本的理论分布。

极值分析上，对比表3：

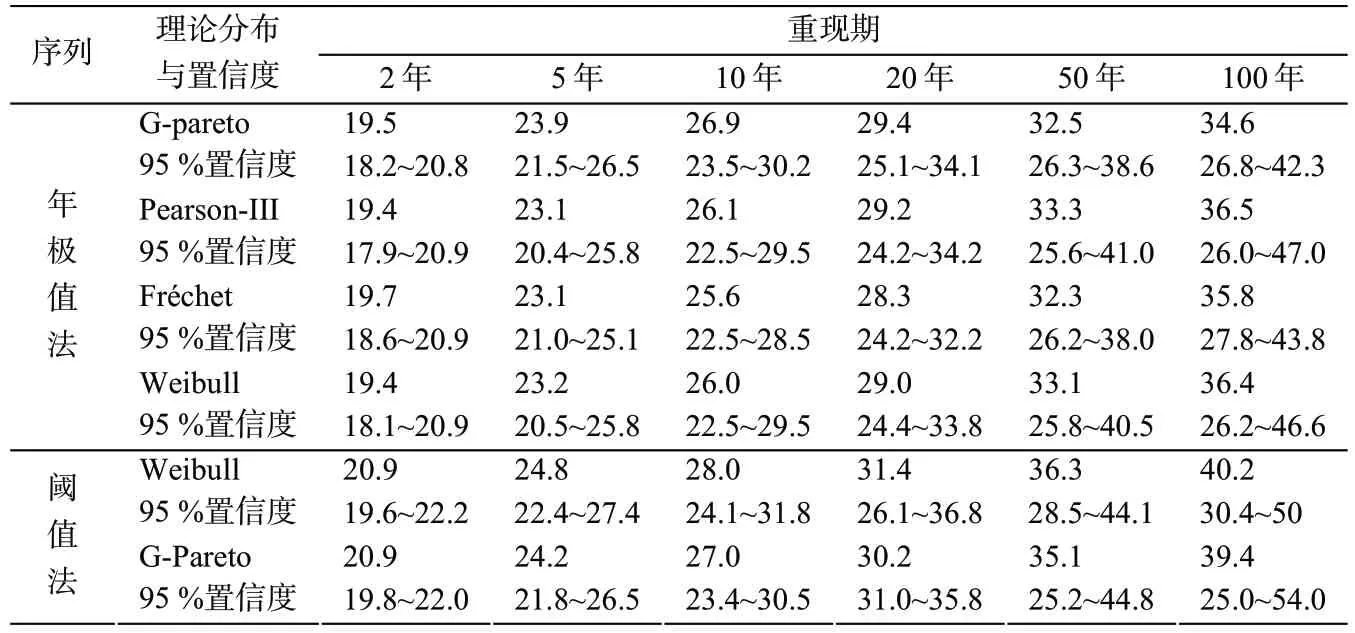
表3 极值风速分析结果(m/s)

1）以上分布对极值风速的拟合结果均较好，且采用不同分布得到的同一重现期设计风速偏差在10 %以内。

2）阈值法样本拟合得到的重现期风速总体略大于年极值样本拟合的结果，且头部大样本均位于估计均值的下方，表明可能存在重现期风速总体估计偏小的风险。

3）为了最大程度的减小设计风速估计偏小的风险，确定外推值的置信区间是非常必要的。本文给出设计极值95 %置信区间上下限值，所有样本均处于95 %置信区间范围内。

4 结语

本文结合菲律宾马尼拉湾某项目极值风速分析，通过比较对理论分布两种快速选型方法，初步表明：两种方法优选推荐的理论分布函数高度一致，但对于个别理论分布存在差异，建议实际应用中应双向验证，从而选出最适宜所选样本的理论分布。基于两类方法推荐的理论分布，进行极值风速估计，初步表明：

1）推荐分布对极值风速的拟合结果均较好，且同一重现期设计风速偏差在10 %以内。

2）阈值法样本拟合得到的重现期风速总体略大于年极值样本拟合的结果，且头部大样本均位于估计均值的下方，表明可能存在重现期风速总体估计偏小的风险。

3）为了最大程度的减小设计风速估计偏小的风险，确定外推值的置信区间是非常必要的。本文给出设计极值95 %置信区间上下限值，所有样本均处于95 %置信区间包络线内。