不同博弈情况下农户间水权交易价格研究

管新建，王宝勇，张文鸽，杜琼英

（1.郑州大学 水利科学与工程学院，河南 郑州 450001； 2.黄河水利科学研究院，河南 郑州 450003；3.黄河流域生态环境保护与修复河南省重点实验室，河南 郑州 450003）

1 引 言

水权是一种特殊的产权，是水资源的所有权、占有权、支配权和使用权等组成的权利束，水资源的稀缺性决定了水资源的价值基础［1-3］。 水权交易是将水权作为一种流动性资源，通过市场机制，诱使用水效率低的用水户节约用水，并把部分水权转让给用水边际效益较高的用水户，从而达到提升社会用水总效率的目的［4］。 我国农业是用水大户，长期以来存在水资源权属不明、水价不合理、缺乏有效激励和制约机制等问题，导致用水效率低下、水资源浪费严重［5-6］。 合理的水权交易定价是水权交易的关键，对水权交易的水量和水价进行研究，对于如何在保障粮食安全的前提下优化种植结构、提高农民收益、促进农民节水意识的提升、提高农业用水效率意义重大［7-8］。

国外在水权交易制度的建设上较为领先，美国和澳大利亚推出了多种水权交易模式，英国的水权交易常为多余水资源的临时性让渡，这些国家的水权具有金融属性，可以作为抵押、担保、贷款的金融工具，促进了水权市场发育［9-10］。 我国水权交易近年来发展迅速，水利部大力引导加快水权交易实践［11］，2014 年1月水利部印发《关于深化水利改革的指导意见》，明确提出建立健全水权交易制度、开展水权交易试点；2014年7 月水利部在宁夏、江西、湖北开展水权确权登记试点，在内蒙古、河南、甘肃和广东开展水权交易试点工作；2016 年1 月国务院办公厅颁布《关于推进农业水价综合改革的意见》，推动建立健全农业水价形成机制，促进农业节水和农业可持续发展；2016 年4 月水利部印发《水权交易管理暂行办法》，为开展水权交易提供政策依据；2016 年6 月中国水权交易中心在北京成立，我国水利相关政策的不断完善推动水权交易迈入新阶段［12］。

在众多学者的共同努力下，我国水权交易定价机制的探索研究发展迅速。 目前我国常用的水权交易定价方法有影子价格法、全成本定价法、实物期权方法、协商定价法、招标定价法等［13］。 影子价格又称最优价格，根据水资源的稀缺程度反映在一定的社会经济产出条件下的水资源优化配置价格，该方法应用范围有较大局限性，结果也难以具体量化。 吴凤平等［14］基于用水投入产出平衡关系，构建转让方影子价格模型，并根据各部门用水限额和总供水量建立受让方影子价格模型，测算双方各用水部门影子价格。 全成本法从成本的角度出发，根据提供用水服务的全部成本确定水价，该方法应用范围广但难以反映实际水权交易价格。宋兰兰等［15］运用逐步结转成本法测算各环节的水价，考虑了上一环节的原水价格、工程成本、费用、税金和利润等因素。 近年来随着研究的深入，一些学者又提出新的水价制定方法。 郑航等［16］基于交易风险和收益平衡，计算市场中交易者的综合收益，得出了集市型交易模式下参与者的最优报价策略，结果表明该方法具有可行性和合理性，可有效发挥市场机制。 殷会娟等［17］将价值流理论应用到水权交易中，采用买卖双方水资源价值量作为水权交易价格，为水权交易价格制定方法提供了新思路。 WU X Y 等［18］提出了基于水资源稀缺价值分析的动态价格调整模型，完善了水权价格动态调整理论体系。 胡晓寒等［19］运用优化理论和博弈理论，研究了在水资源总量紧缺状况下，如何确保集体收益最大和交易双方共赢的农户间水权交易。

本文以农户间水权交易为研究对象，引入水分生产函数对农户的用水生产能力进行量化，结合博弈论思想，分别以集体利益最大化为目标函数进行合作博弈和以个人利益最大为目标函数进行非合作博弈计算，把水资源总量控制和粮食安全保障作为约束条件，建立水权交易定价模型，首先计算不同博弈方案下的水权交易均衡价格，然后根据灌溉定额、种植面积和初始水权分配量计算交易水量，最后根据交易水价、交易水量和作物市场价格等计算利益增值。

2 研究方法

2.1 理论框架

产量与资源投入量之间的函数关系称为生产函数。 在其他资源投入量不变的前提下，水资源作为一种必要的生产要素，投入量不同，农作物的产量也不同，可以用生产函数建立水权与作物产量的关系［19］。水分生产函数在水权交易价格制定中应用广泛，它主要有以下优点：①在其定义域内连续可导；②先单调递增后单调递减且二阶导数小于零，为严格的凸函数。水分生产函数能很好符合灌溉用水户的用水边际效益递减的特点以及反映用水效益和用水量之间的关系，其表达式为

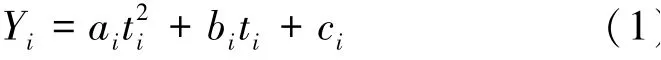
式中：Yi为第i种作物的单位面积产量，kg／hm2；ti为第i种作物的灌溉定额，m3／hm2；ai、bi、ci为水分生产函数的参数。

在水资源优化配置中，博弈论思想应用较为广泛。博弈论是研究两个或多个参与者在完全理性的情况下为了实现自身利益最大化而选择适合自己的最优策略或者策略集。 按照博弈参与者之间的合作关系，博弈可分为合作博弈和非合作博弈：合作博弈是在系统收益最大的约束条件下寻求最优策略，因而强调团队，对于参与者而言能够获得不少于合作前的收益，对于合作博弈集体而言总收益大于合作博弈前各参与者收益之和，参与者之间有强有力的约束协议；非合作博弈没有约束的协议，强调个体行为，各参与者独立自主决策，从策略集中选择自身收益最大化的策略。 合作博弈与非合作博弈水权交易模型理论框架见图1。

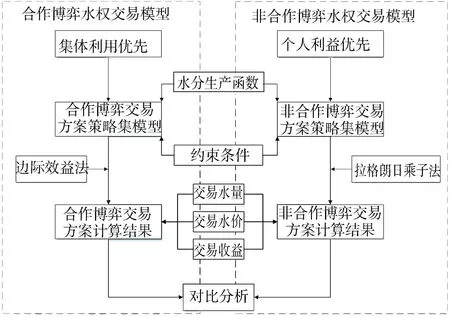
图1 合作博弈与非合作博弈水权交易模型理论框架

2.2 灌溉用水户水权交易成本价格

水权交易成本价格主要由工程成本、风险补偿成本、生态补偿成本、经济补偿成本4 部分组成［9］，灌溉用水户间的水权交易成本价格包括节（输）水工程的建设费、维护费、更新改造费以及必要的生态补偿和经济利益补偿费等。 水权交易成本价格计算公式为

式中：PC为水权交易成本价格，元／m3；C为水权交易总成本，元；T为水权交易年限，a；WT为年水权交易量，m3。

2.3 合作博弈情况下农户间水权交易价格

合作博弈情况下，农户间水权交易在政府部门的约束保证每个农户利益不受损失的前提下，追求集体效益最大化。 每个农户的综合收益包括其购买水权进行农业生产活动带来的收益、水权用不完时出售得到的收益或者水权缺少时购买产生的负收益。 农户的收益计算公式为

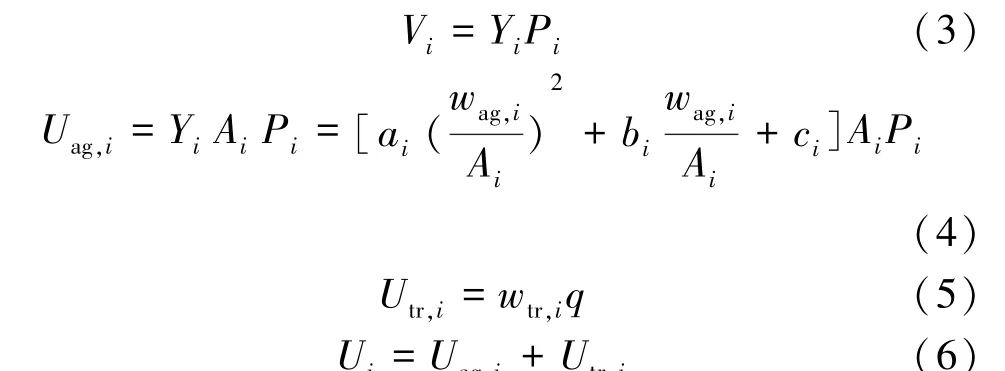
式中：Vi为农户种植作物的单位面积产值，元／hm2；Pi为农户种植作物的出售单价，元／kg；Uag，i为农户进行农业生产活动产生的收益，元；Ai为农户的种植面积，hm2；wag，i为农户用于种植活动的用水量，m3；Utr，i为农户卖出或者买入水权产生的收益（当农户有多余水权卖出时产生的收益为正值，当需要从水市场购买水权时产生的收益为负值），元；wtr，i为农户交易的水量，m3；q为水权交易价格，元／m3；Ui为农户的综合收益，元。

根据集体收益最大化原则，建立合作博弈模型。

式中：wi为农户的水权分配量，m3；R为所在地区粮食总需求量，kg；E为人均粮食需求量，kg／人；Z为所在地区总人口数；S为复种指数；A为所在地区农作物总播种面积，hm2。

由边际效益函数可知，在水权分配足够的情况下，当作物产量函数Yi对灌溉定额ti的导数为0 时求得的ti为作物的最佳灌溉定额，作物产量最大；当水权分配不足时为达到集体效益最大化，各农户的边际效益值应相等，此时水权交易均衡价格即为边际效益值，交易水量由此时的灌溉定额计算出的灌溉水量与初始分配水权的差值来确定。

2.4 非合作博弈情况下农户间水权交易价格

在非合作博弈的情况下，农户参与水权交易的目的就是为了实现自身综合收益最大化，根据自身实际需要决定是否参与水权交易以及与谁进行水权交易，从策略集中选择一个对自己最有利的策略。 由于用户的初始水权量是确定的，因此其在具有一定水权的基础上结合边际效益做出出售水权还是购买水权的决定。 在非合作博弈的情况下，农户的综合收益为

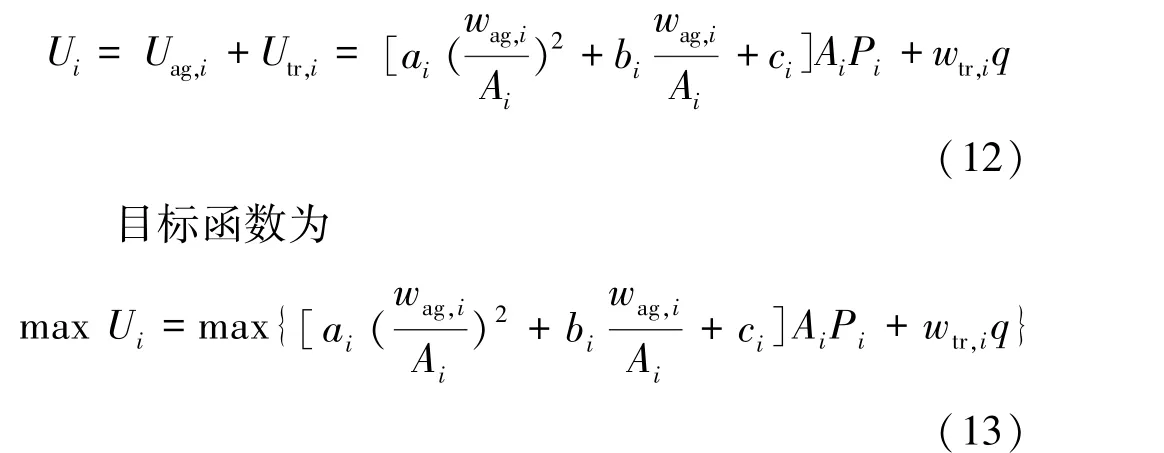
约束条件也为用水总量约束和粮食安全约束，可使用拉格朗日乘子法求解。 拉格朗日函数表达式为

假设水市场中有n个参与者，各个参与者分别寻求各自的综合收益最大化，则可得到水市场中水权交易均衡价格：

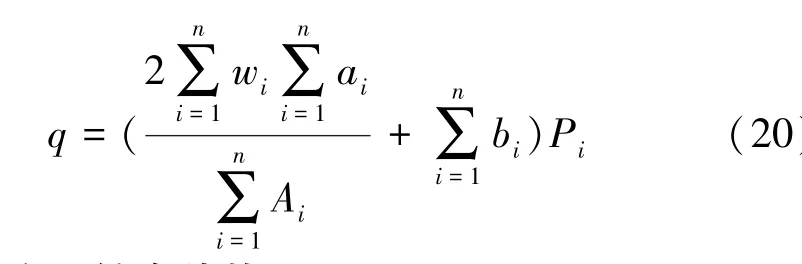
2.5 水权交易综合价格

水权交易价格应综合考虑成本价格和在不同博弈情况下的均衡价格，因此可以得到水权交易综合价格模型：

式中：P综为水权交易综合价格，元／m3。

3 实例分析

结合灌区农户节水的实际情况，由于只考虑了用水结构调整，水权总分配量没有变化，只是根据农户生产能力不同对灌溉定额进行调整，因此本研究的水权交易不考虑成本价格，水市场均衡价格即为水权交易综合价格。

3.1 研究区概况

选取内蒙古河套灌区杨唐渠灌域进行研究，该地区水资源短缺，主要通过引水渠从过境的黄河引水。研究区内有N1、N2、N3共3 个农户，N1种植小麦（面积45 hm2）、N2种植棉花（面积20 hm2）、N3种植玉米（面积32 hm2）。 该地区水资源分配量为40 万m3，考虑渠系间与田间输水损失，灌溉水利用系数为0.8，初始水权按照公平性原则，根据面积权重大小进行分配，农户N1、N2、N3分配的初始水权分别为14.85 万、6.59万、10.56 万m3。

3.2 参数确定

本文研究区小麦和玉米属于粮食作物，按照我国人均粮食需求不低于400 kg／人的标准计算［20］，复种指数取1.05。 作物的水分生产函数参数a、b、c可以通过对实验数据回归拟合来确定，也可以通过地区经验值来确定。 本文通过河套灌区当地经验值确定参数，小麦、玉米、棉花的水分生产函数分别为

3.3 合作博弈情况下交易水量及价格计算

当地市场价格，小麦为1.94 元／kg、棉花为16.12元／kg、玉米为2.26 元／kg。 合作博弈情况下该地区的3 个农户都可自主选择是否参与水权交易合作联盟，总共可分为以下5 种情况：方案①为N1、N2、N3都不参与交易，综合收益分别为70.87 万、109.60 万、60.39万元；根据式（7）～式（11）计算交易水量和交易价格，根据式（3）～式（6）计算种植收益、收益增值和综合收益，其余4 种方案的计算结果见表1～表4。

表1 方案②合作博弈下N1 和N2 参与交易、N3 不参与交易的计算结果

表2 方案③合作博弈下N1 和N3 参与交易、N2 不参与交易的计算结果

表3 方案④合作博弈下N2 和N3 参与交易、N1 不参与交易的计算结果

表4 方案⑤合作博弈下N1 、N2 、N3 都参与交易的计算结果

3.4 非合作博弈情况下交易水量及价格计算

在非合作博弈情况下，每个农户都可自主选择是否参与水交易，所以总共可分为以下5 种情况：方案①农户N1、N2、N3都不参与交易，方案②农户N1和N2参与交易、N3不参与交易，方案③农户N1和N3参与交易、N2不参与交易，方案④农户N2和N3参与交易、N1不参与交易，方案⑤农户N1、N2、N3都参与交易。根据式（18）～式（20）计算交易水量和交易价格，根据式（3）～式（6）计算种植收益、收益增值和综合收益，方案①～方案④与合作博弈情况下的前4 种方案的交易水量、交易价格和收益增加值计算结果均相同，方案⑤计算结果见表5。

表5 方案⑤非合作博弈下N1 、N2 、N3 都参与交易的计算结果

4 结果与讨论

合作博弈和非合作博弈下的方案①均为N1、N2、N3都不参与水权交易，则他们的综合收益仅为各自作物种植的收益，因此把该方案作为基本方案，对比研究其他方案的交易水量、交易价格及总收益增值，计算结果见表6，各农户综合收益见图2。

表6 不同方案的交易水量、交易价格及总收益增值计算结果

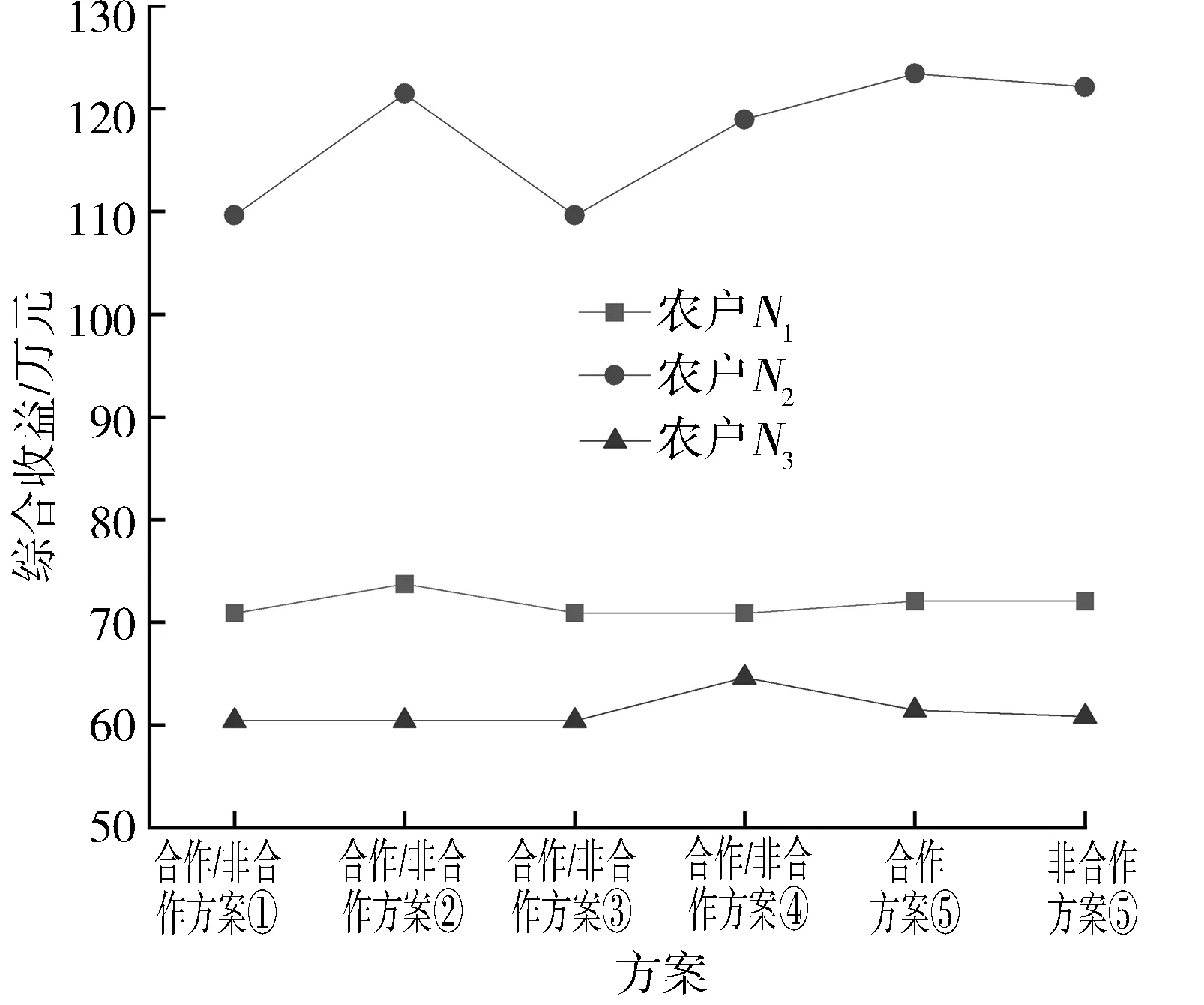
图2 不同方案下各农户综合收益

（1）通过模型构建以及实例计算可知，农户的综合收益由种植收益与水权交易收益两部分组成，交易水量与交易价格不仅与种植作物的水分生产函数、种植面积和作物市场价格等因素有关，还与参与水权交易的农户有关。 当参与水权交易的农户只有两个时，采用非合作博弈水权交易模型计算出的水权交易价格、交易水量与合作博弈水权交易模型计算出的结果相同，此时农户个人综合收益最大与二者集体收益最大不冲突。

（2）在合作博弈情况下，最佳策略是全部农户都参与水权交易，当每个农户的边际效益值一样时集体收益最大，此时N1和N3分别向N2出售了21 428 m3和15 032 m3水权，水权交易价格为2.205 元／m3，3 个农户的总收益为257.10 万元，比都不参与水权交易收益多16.24 万元。

（3）在非合作博弈情况下，由于每个农户都追求个人收益最大，N1与N3无论在对方是否参与交易的情况下，其最佳交易策略都是与N2进行水权交易，N2的最佳交易策略是同时与N1和N3进行交易以获取更多的水权，因此最后会达成三者之间交易的纳什均衡，此时N1和N3分别向N2出售了21 496 m3和3 136 m3水权，水权交易价格为2.208 元／m3，三者的总收益为254.93 万元，比都不参与水权交易收益多14.07 万元，但是此时的集体收益反而比N1与N2进行交易、N3不参与水权交易时小。

（4）在合作／非合作博弈下的方案②（N3不参与水权交易）时，N1和N2进行水权交易的集体收益增值为14.71 万元；合作／非合作博弈下的方案③（N2不参与水权交易）时，N1和N3进行水权交易的集体收益增值仅为0.04 万元；合作／非合作博弈下的方案④（N1不参与水权交易）时，N2和N3进行水权交易的集体收益增值为13.58 万元，说明在水权交易双方边际效益相差较大时，才能更大程度上使水资源从低效益向高效益转移。

（5）将合作博弈下的方案⑤与非合作博弈下的方案⑤对比可知，当多个农户参与水权交易时非合作博弈水权交易的集体收益小于合作博弈的集体收益。

5 结 语

水权交易价格制定是水权交易的核心，为实现水资源的优化配置并确保每个水权交易参与者的利益，本文针对农户间水权交易价格开展研究，建立水权交易定价模型，并将其应用到内蒙古河套灌区杨唐渠灌域，计算不同博弈情况下不同方案的水权交易价格、交易水量和收益变化。

本文建立的基于博弈论与水分生产函数的农户间水权交易价格计算方法，可以为缺水地区水权交易价格与交易水量的制定提供依据，丰富了现有水权交易价格理论。 合作博弈强调团队理性，非合作博弈强调个体理性，与非合作博弈相比，合作博弈能实现集体收益的最大化。 地方政府相关部门应制定相应措施，完善水权交易制度，提高农户水权交易积极性，从而达到水资源优化配置的目的。