盾构螺旋机叶片截面形状对其耐磨性的影响

0 引言

1 理论基础与模型假设

根据参考文献[1]的分析，盾构螺旋机的磨损最主要是磨粒磨损。同时针对磨粒磨损的分析采用拉宾诺维奇模型及其公式，见图1所示。

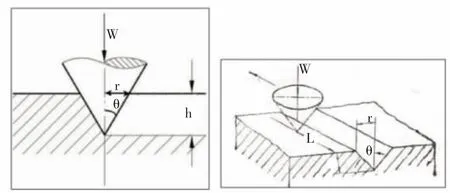
图1 拉宾诺维奇磨粒磨损模型图

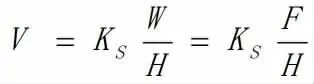
为更便于量化，假设叶片截面为L型，其各处尺寸见图2所示。其中，设啄=a×啄。考虑到啄1为支撑结构及抵抗土体磨损的最小厚度，此值在设计初期，将根据结构的受力计算得出啄1的最佳值，因此我们可以设啄1为定值常量。再根据拉宾诺维奇提出的磨损微观模型及磨损量计算公式，求出a的最佳比例值。

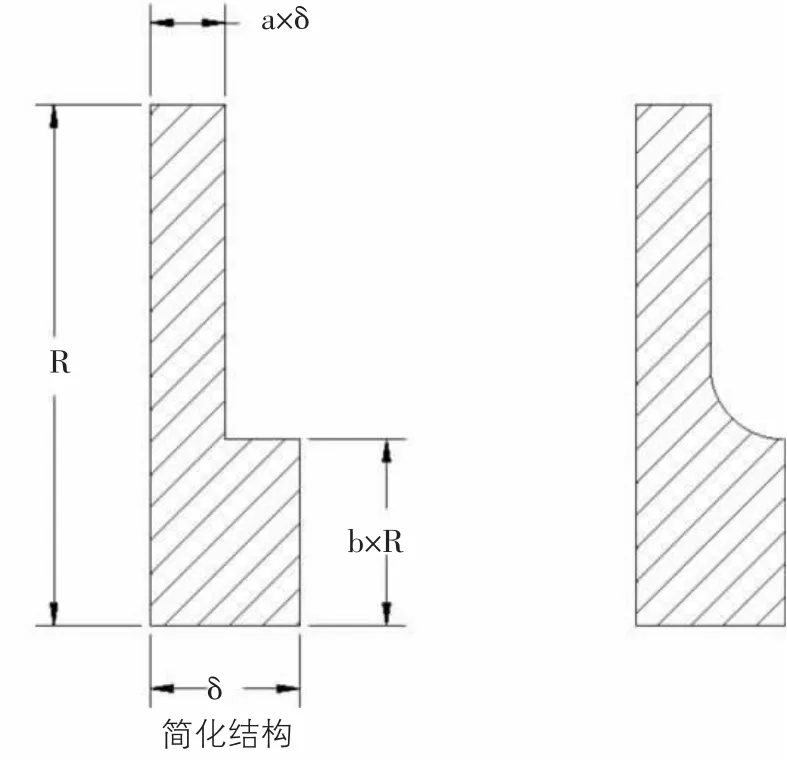
图2 L型叶片截面尺寸图

为便于问题分析、简化计算，进一步做以下假设：①各种磨损均为磨粒磨损；②螺旋机叶片的重量是厚密度与叶片当量厚度的乘积；③由于实际应用中一般叶片与筒体选用的耐磨材料相同，同时叶片与筒体之间的作用是相互的，所以这里假设叶片与筒体的磨损系数和耐磨硬度是相同的。④由于研究的是叶片厚度与螺旋机磨损量的关系，螺旋机的其它性能参数均作为定量考虑。例如筒径、节距、材质等均为定值。

2 公式推导与计算

根据磨粒磨损显微切削模型，叶片与筒体之间的磨损量可以由下面公式计算得出。

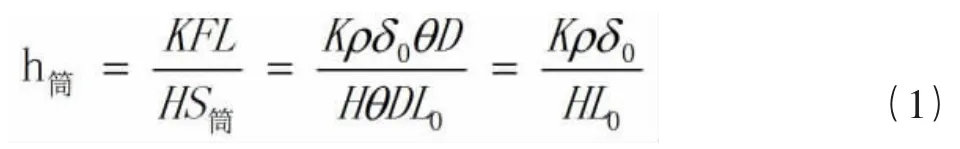
其中h为筒体厚度磨损量；

K为综合磨损系数；

云铜总厂研发中心利用工业盐在高氯体系下实现了铅、锑、铋的定向分离[1]，在液固比为L∶S=7∶1、温度80 ℃、时间2 h、NaCl浓度为6 mol/L的条件下，铅的脱除率为89.63%，锑的脱除率为13.97%，铋的脱除率为26.67%。虽然实现了大部分铅的分离，但该体系下金、银也存在一定的分散，回收难度较大。

L为筒体受叶片重力区域长度；

δ为叶片截面的当量厚度；

ρ为叶片的厚密度；

H为叶片耐磨材料的硬度。

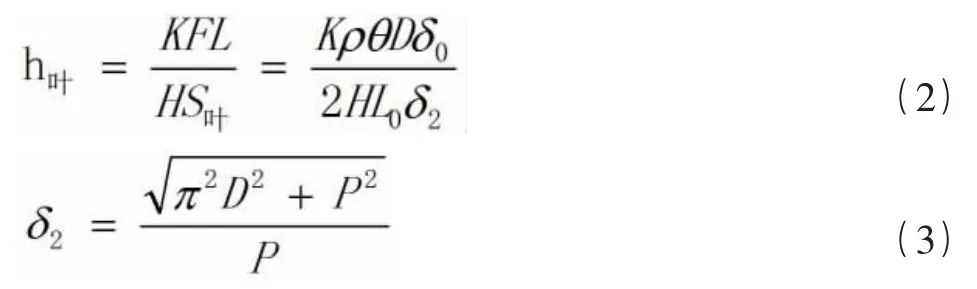
其中h为叶片径向磨损量；

D为筒体内径；

θ为筒体底部与叶片接触的角度；

δ为叶片摩擦面的当量宽度；

P为螺旋机叶片节距。

考虑到螺旋机的输送能力，单位输送量下磨损量对实际应用更有意义。所以我们用式（4）来考量磨损量的多少。x为h与h在磨损量考量中所占的比重。由于筒体的厚度相对于叶片半径较小，且磨穿筒体后，螺旋机将无法正常工作。所以x一般取小于1的数值。

根据螺旋输送机输送能力公式：

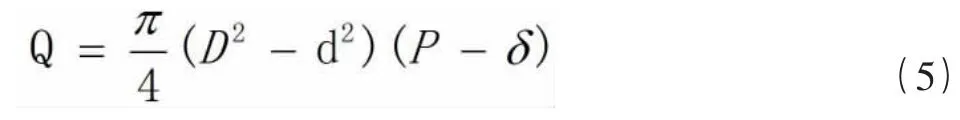
将公式（5）、（1）、（2）、（3）代入公式（4）得：

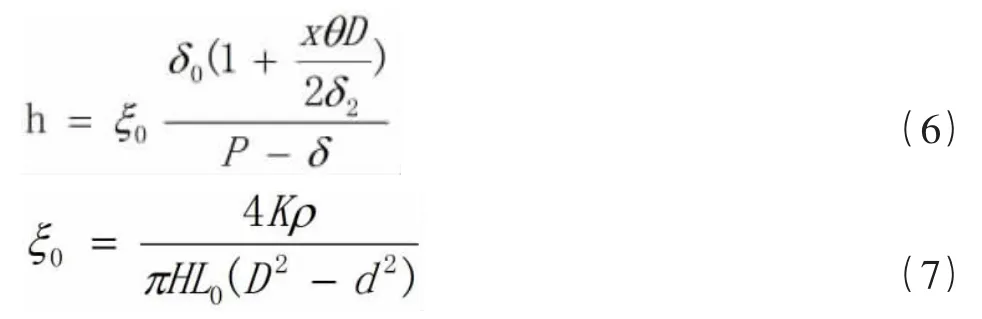
将h对a求导并取0得：

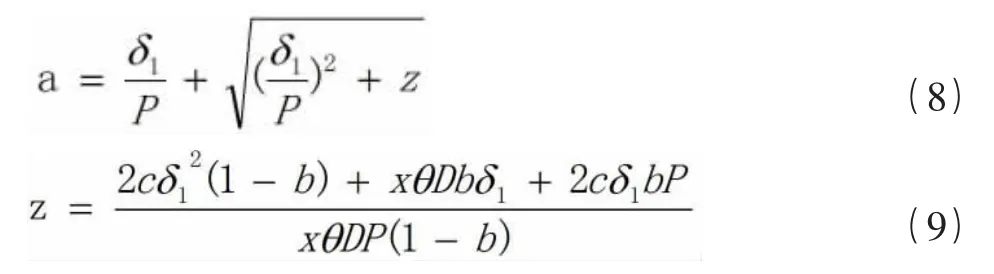
经过数值验证，a为此数值时h是最小值。将常用直径螺旋机的各项参数代入式（8）中，同时x值取0.5时得a值如表1所示。

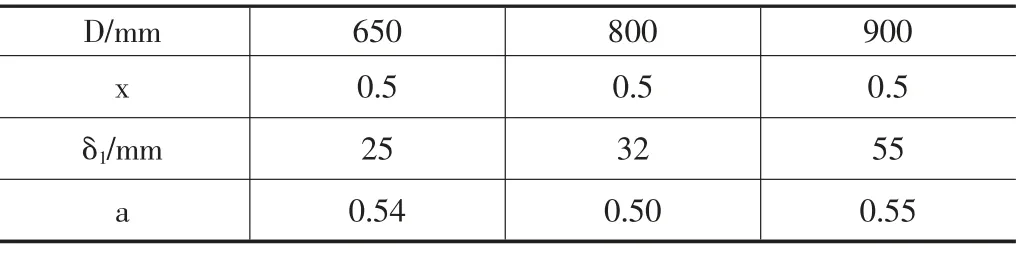
表1 不同直径与叶片厚度情况下计算出的a值

市场上流行的几家进口品牌盾构机的实际螺旋输送机的叶片厚度与外周耐磨块的厚度值参见表2。

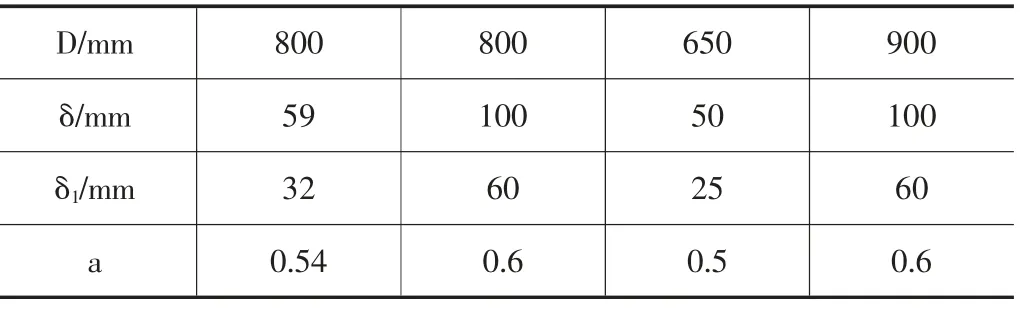
表2 不同直径、厂家叶片厚度数值

通过表1和表2中的a值对比看，上述磨损模型和计算公式的结果与现在主流盾构机厂家的螺旋机叶片设计尺寸非常接近。证明本文中的理论计算与实践积累是符合的。我们也可以进一步通过实际案例，来对比查看螺旋机的磨损位置和磨损情况与本文假设模型是否一致。

3 实际案例对比

本文这里从市面常用盾构机中取一些具有代表性的几种机型，分别对比他们在使用中的摩擦位置以及截面形状与本文上诉假设模型是否符合。进而验证假设模型及其计算出的比例值是否正确。

如图3所示为某900直径的螺旋机叶片，其采用的方案是在叶片外周焊接高耐磨材质的耐磨块。耐磨块的宽度比叶片本体宽，其宽度比例值a=0.6，参见图4。同时在叶片表面的外周方向上增加了耐磨焊，从而补强磨损较重区域的耐磨性。耐磨块的宽度与叶片宽度比例值与本文的公式结果是相符合的。同时耐磨焊的位置的选择，也与本文的磨损假设模型保持一致。

图3 某900直径螺旋机叶片图

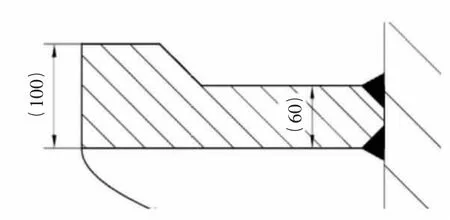
图4 某900直径螺旋机叶片截面尺寸图

经过施工掘进后，磨损后的螺旋机叶片的照片见图5。不难看出，通过施工后磨损情况的照片，我们可以看到螺旋机下叶扇片的磨损较轻，上叶扇片的磨损略重一些。叶片径向外周的磨损最为严重。这个与上述假设模型也保持了一致。

图5 某900直径螺旋机叶片磨损情况图

如图6所示为某800直径的螺旋机叶片，其采用的方案是在叶片外周布置螺栓固定的耐磨块，针对磨损严重的区域采用了可拆换式设计，为施工的维护保养以及日后的修补提供了方便。

图6 某800直径螺旋机叶片图

在耐磨设计方面，其在叶片本体的径向外周焊接耐磨焊，保护的区域与前述900直径机是一样的。这个与本文的磨损模型分析结果也是一致的。厚度的比例值是0.54，与本文的结论公式也是相符合的。图7为某800直径螺旋机叶片截面图。

图7 某800直径螺旋机叶片截面图

经过施工后，螺旋机的磨损情况照片见图8。可以看出，螺旋机叶片的磨损程度的顺序依然是叶片径向外周最强，其次是上叶扇片，最轻是下叶扇片。这个与前述机型的实际情况一样，同时也与本文的磨损模型保持一致。

图8 某800直径螺旋机叶片磨损情况图

该可拆卸耐磨块对叶片本体钢结构产生了有效保护，本体钢结构磨损量并不大，在后续的维修改造中仍可继续使用。但由于耐磨块的连接部位被泥土填塞严重，后期的更换可操作性并不大。同时，由于是螺栓连接，遇到较大撞击外力时耐磨块会较易脱落，虽然案例中只有极个别脱落现象，但这依然是不可忽略的问题。

4 结论

由于螺旋机在施工中的重要性，现阶段其叶片设计越来越倾向于更大更重方向发展。这与理论上的最优化设计不相符。螺旋机叶片厚度的设计也并非越厚越好。本文根据磨粒磨损显微切削模型，推导出公式（8）作为“L”型螺旋机叶片宽度比例的理论最佳值，为设计提供了理论支持。同时，根据实际案例的叶片设计和磨损情况，验证了该模型的可行和正确。可以在后续的设计中参考使用。

另外因磨损系数与很多因素有关，单凭计算很难得到具体数值。所以本文只是按照理论计算寻找最优值，未考虑最优值与其他值的磨损偏差量。若能用实验测得各种地质对某种耐磨材质的磨损系数，将可以优化计算公式且更深入分析叶片截面形状和厚度对螺旋机耐磨性能的影响。基于以上的不足，也希望本文能够抛砖引玉，希望后续能有更多的单位和个人参与到盾构螺旋机磨损的研究中，测试出磨损试验的数据或引进更先进和专业的理论模型对其进行分析，从而推动盾构机制造行业的发展。