Expected adult lifespan in tropical trees:Long-term matrix demography in a large plot
Richard Condit
a Morton Arboretum, 4100 Illinois Rte. 53, Lisle, IL, 60532, USA
b Institute for Marine Sciences, University of California, Santa Cruz, USA
Keywords:Tree lifespan Tropical tree Matrix demography
ABSTRACT
1. Background
Lifetime demography of tropical forest trees means tracking the fate of juveniles until they become reproductive adults.But trees live longer than research projects, so complete life-tables can only be created by splicing together short-term measurements from trees monitored in census plots (Usher, 1966; Condit et al., 1993; Chien et al., 2008; Zuidema et al., 2010; Picard and Liang, 2014). Though tree-ring studies of tropical trees have proliferated, producing lifetime growth trajectories(Brienen and Zuidema, 2006; Brienen et al., 2010; Rozendaal and Zuidema, 2011; Alfaro-S′anchez et al.,2017), these cannot address survival and thus do not provide complete life-tables. Long-term and large-scale plot samples are needed. The Barro Colorado 50-ha plot in Panama was designed to create complete life-tables.
Short-term plot measurements have generated hypotheses about demographic guilds of tropical trees,focusing on how species with varying growth and mortality co-exist(Hartshorn,1980;Denslow,1980;Stearns,1999; Salguero-G′omez, 2017; Rüger et al., 2018). Hypotheses about coexistence are necessarily about lifetime demography, yet the lifetime impact of tradeoff between growth and survival has not been examined.Here I test the impact of the growth-mortality tradeoff on reproductive lifespan using transition matrices constructed from observations in the Barro Colorado plot. I demonstrate analytical solutions to lifetime demographic parameters from the matrices, then examine how these parameters vary across the full spectrum of growth and survival rates(Rüger et al., 2011a,b).
The primary question is whether tree species across the fast-slow life history axis are in demographic balance.I examine this by calculating the expected adult lifespan of saplings at 1 cm dbh. The expected adult lifespan is a key demographic trait because it determines the potential reproductive output for the average juvenile entering the population.To be in balance,the fast growth rate of pioneer trees must overcome their high death rates, leading to an adult lifespan equal to slow-growing,shade-tolerant species. I also calculate two other demographic results closely related to the expected adult lifespan:the probability of reaching adulthood (maturation probability) and the time it takes to reach adulthood(maturation time),both for the average 1-cm sapling.Markov chain theory offers analytical formulations for a sapling’s expected adult lifespan and probability of reaching adulthood(Kemeny and Snell,1960;Iosifescu,1980).
Analytical solutions allow theoretical analyses of elasticity, relating the key demographic outcomes to variation in transition parameters. In particular, I use theoretical predictions of adult lifespan along the observed growth-mortality tradeoff (Rüger et al., 2020) to examine whether the upper end of the axis (fast growth) achieves adult lifespan equal to the lower end (slow growth). This extends existing work on matrix demography, which seldom includes analytical results (Franco and Silvertown,2004;Doak et al.,2021).
2. Transition matrix demography
2.1. Overview
Matrix models are a standard tool in plant demography, from the Lefkovitch matrix to Integrated Projection Models, and there are many varieties of matrices (Lefkovitch, 1965; Caswell, 2001; Ellner and Rees,2006;Doak et al.,2021).In order to make theoretical predictions about the growth-survival tradeoff, I maintain that a simplified approach best reveals the basic underlying demographic consequences of a growth-survival tradeoff. For this reason, I omit reproduction and focus on expected adult lifespan,and I construct matrices with a small number of classes between which growth probabilities are near constant.
The demographic matrix starts by dividing individuals into categories based on stem diameter. This defines the population as a vector Ni, the number of individuals in each size class i. Given two successive measurements, a transition probability between any two size classes is estimated by counting the proportion of Nithat advance to a larger size class,j >i (growth), remain in class i (stasis), and how many die. The Barro Colorado 50-ha plot was designed to include large sample sizes of many tree species, and for the most important species of the forest, demographic estimates are strong (Hubbell and Foster, 1983; Condit,1998). Moreover, multiple censuses provide replicate transition estimates(Condit et al., 2017).
From a standard transition matrix, I calculate three lifetime demographic parameters,all expectations for the average 1-cm sapling:1)adult lifespan,2)maturation probability,and 3)maturation time.I then explicitly address two common concerns about population matrices(Picard et al., 2003; Zuidema et al., 2009; Doak et al., 2021): 1) that results are dependent on the size classes defined,and 2)that the matrix approach omits temporal autocorrelation in the demographic parameters.To address these concerns,I tested whether lifetime estimates were robust to variation in size classes, and I devised a new approach that allows transition matrices to include autocorrelation as memory of prior transitions.
2.2. Lifetime demographic results from the transition matrix
I first illustrate the two main matrices I used and state formulae for the key demographic results. Appendices 1-2 include full derivations of the formulae and add descriptions of alternative matrix constructions.Since I use derivations from Markov chain analysis of transition matrices(Kemeny and Snell, 1960), I follow conventions in the Markov-chain literature, using row-stochastic matrices (Caswell, 2001). This means that the fate of an individual is found along a row, and the sum of transition probabilities along a row is 1; this is the transpose of a Leslie matrix(Leslie, 1945).
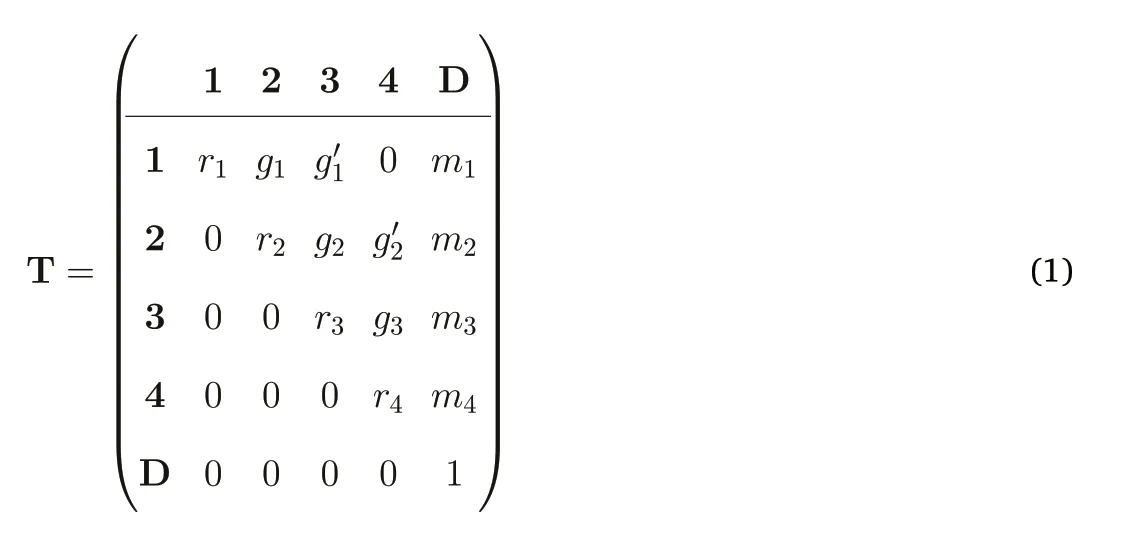
For the basic matrix, I divided trees into four size classes, three juvenile and one adult.A Leslie matrix would stop at four classes,but a full transition process requires one more, because dead trees must be included, leading to a 5×5 transition matrix, T. Size categories 1–4 are labeled with boldface and D is the category for dead trees:Element tijof T,at row i and column j,is defined as the probability that a tree in size class i in one census transitions to class j in the next census.The diagonal of the matrix has stasis probabilities,each a probability that a tree in class i remains there one census later; tii= ri(r for remain to emphasize that it differs from survival).Elements above the diagonal are growth transitions,and the final column is the death transition,so ti5=mi,with m for mortality(j= 5 is the D class).

Equation 1 describes an absorbing Markov process because all trees are eventually absorbed into the death state, enforced by row 5 in the matrix. The demographic questions are about the pathway trees follow before death: how long it takes to die, what proportion live until adulthood, and expected lifespans. It is a Markov process because the transitions at one time step are independent of past times.There is no memory.Kemeny and Snell (1960) and Iosifescu (1980) give many examples of transition matrices,some non-absorbing,others with multiple absorbing states. By adding additional categories, it is not a difficult step to a Markov process that includes memory.
2.3. A transition matrix with memory
The demographic flaw in a Markov process is that trees might have unrealistically high growth. This can happen because a tree that grows from class 1 to class 2 at one time step might immediately grow from 2 to 3 at the next step. Zuidema et al. (2009) and Picard and Liang (2014)examined fast growth due to consecutive transitions. They reached opposite conclusions, so here I test explicitly the impact of adding memory to the transition process while retaining the Markov assumption.This is possible if the matrix has two subclasses within each size class,one for trees that just grew there and another for trees that were already there. This means a 9×9 transition matrix to cover four size classes:

Within the first size class are two subclasses, labeled 1.1 and 1, and likewise for classes 2 - 4. When a tree first grows from one size to the next,it arrives in the.1 subclass and it remains there for one time step(or dies). All transition probabilities must also be split into two, and here I redefine symbols in order to avoid double subscripts.Growth probabilities for size classes 1,2,3 are labeled f,g,and h,and each has a subscript 1 for trees that just arrived in a class(g1,f1,h1)and no subscript for trees already in a size class.The residence probabilities,for remaining in each size class,are r,s,t,and u,and these likewise are paired,with and without subscripts.The final column has death probabilities,here written as one minus the sum of growth and residence to reduce the number of symbols.
Consider the example of a tree starting life as a new sapling,in subclass 1.1.It has probability f1of growing,which means entering subclass 2.1,the initial subclass in size class 2.It has probability r1of remaining in size class 1,but that means graduating from 1.1 to 1.Or it might die with probability 1-r1-f1.Once it is in category 1,it can reside there with probability r or grow to 2.1 with probability f.The same rules repeat once a tree reaches 2.1, using probabilities g, g1for growth and s, s1for residence,and so forth.
This same approach can accommodate three subcategories per size class,and this is written out in Appendix 2.It could be extended to more subcategories,but I stopped at three.
2.4. Deriving expected lifespan
The primary question about adult lifespan is about a tree starting as a sapling,in class 1.Given a population of N1=100 saplings,what is their expected time spent as adults? This expectation is an average of two groups:trees that die before adulthood,and thus have an adult lifespan of zero, and trees that reach adulthood and spend at least one time step there.The mean adult lifespan might be a small number,much less than 1 if most of the 100 saplings die before adulthood.
The expected adult lifespan of a sapling has a straightforward analytical solution from the transition matrix T (Kemeny and Snell,1960), and if two-step growth is zero, it extends to any number of size classes.There are also exact solutions for matrices with one-or two-step memory,though extending those to >5 size classes is more complicated.
Define Lijas the expected lifespan in size class j for an individual starting in size class i. One of the basic calculations from Kemeny and Snell(1960)leads to the expected lifespan in any of the size classes for an individual starting in class 1:

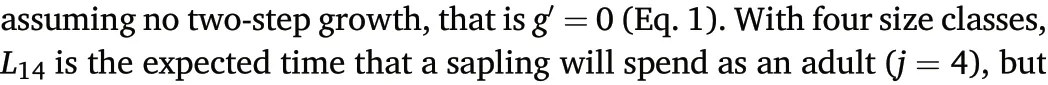

where α=fr1+f1(1-r),β=gs1+g1(1-s),and δ=ht1+h1(1-t).The two terms L1.1,4.1and L1.1,4are needed because adults include the last two subclasses,4.1 and 4(Eq.2).Equation 5 gives the expected adult lifespan of a sapling just entering category 1.1. I show analytical solutions for matrices with memory using only four size classes and one-step growth.
Comparing Equations 3 and 5 suggests how adult lifespan will change with the addition of memory. In slow growing trees, it is reasonable to consider the immediate growth terms f1,g1,h1~0.Then the numerator in Equation 5 is left with αβδ = fgh, the product of all growth terms, as in Equation3,plusanextra1-u+u1.Denominatorsin thetwoequationsare identical.The growth terms f,g,h should be increased relative to growth in the original matrix(no memory),while empirical results suggest 1-u+u1<1,because trees that just grew usually have lower death rates than resident trees.The resulting adult lifespan from Equation 5 is thus neither obviously increased nor decreased relative to Equation 3. My analysis should be compared closely with Picard and Liang(2014).
2.5. Deriving maturation probability
The probability that a sapling reaches adulthood, or maturation probability, is a straightforward derivation because the expected adult lifespan after reaching adulthood,Ljj(where j is the adult class),is easy to calculate.It requires no matrix theory because mortality rate as an adult remains constant,so

where L1jis the expected adult lifespan of a sapling(from Eqs.3–5).This follows from the definition of average expected lifespan,which declines from Ljjto L1jin proportion to the fraction of saplings that never become adults,all of which have an adult lifespan of zero(Appendix 1).
2.6. Deriving maturation time
The final calculation is the time it takes for a sapling to reach adulthood, or the maturation time. I have not found this published (Kemeny and Snell, 1960; Iosifescu, 1980; Caswell, 2001), and I do not have an analytical solution for the matrices in Equations 1 and 2. There is an analytical solution,however,for a simpler matrix with constant growth g and residence r,where gi=g and ri=r in every size class,and omitting two-step growth.Then the mean number of time steps it takes a sapling to reach adult class j is

Appendix 1 gives the derivation. This remarkably simple way of estimating maturation time should provide many insights into matrix demography and lifespan,but I do not pursue it here.
2.7. Numerical estimates
In order to calculate the key demographic traits numerically, from any transition matrix, I used numerical projections with observed matrices.Since the questions are about the fate of saplings in class 1,the vector of initial population size,N,had N1=1 and Ni=0 for i >1.The population vector at step x is N′=NTx,since the transition matrix after x steps is Tx,meaning T raised to the xth power(Kemeny and Snell,1960).The number of adults at time x is N′a,where a is the adult(terminal)size class.I calculated maturation time and maturation probability by finding the fraction of saplings recruiting to class a in each time step.The number of adults recruiting between x-1 and x is

where N′a is the number of adults at step x,Nathe number at x-1,and rais the residence probability in class a.This is the difference between the number in class a at time x and those that were already in class a at time x-1 and remained until x.In the matrix with memory,the calculation is easier, because newly recruited adults are only in subclass a.1 and the second term in Equation 9 is unnecessary.
The number of adults recruiting is A=Σax,summed over time steps until ax→0. The maturation probability is P1j= A/N1, and the maturation time is the mean of the distribution ax.The expected adult lifespan for all N1saplings at the start can then be found using Equation 7.
Numerical calculations are possible on any transition matrix,with no restrictions on growth steps, with or without memory. The only limitation was that I did not calculate transition matrices with two-step memory in the larger tree species(Table 1).
3. Field methods
3.1. Plot and census
The 50-ha plot on Barro Colorado Island was first censused in 1981–1982,then recensused every 5 years from 1985 through 2015.All stems ≥1 cm diameter-at-breast-height (dbh) were mapped, measured,and identified in each census (Hubbell and Foster, 1983; Condit, 1998;Condit et al.,2017).A total of 423,617 individual trees have been tagged over 35 years,where the individual is defined as a genetic unit,meaning all stems from one base. Though all stems were measured, here I only used the largest stem per individual. Stems were measured at breast height, 1.3 m above the ground, except where the stem was swollen or misshapen at that height.Growth rates are included here only when the same stem was measured at the same height in consecutive censuses; I refer to stem diameter as dbh(diameter-breast-height),even if it was not 1.3 m. Trees were considered dead when all stems within an individual died. In 1982 and 1985, stems <55 mm dbh were measured with a precision of only 5 mm, but starting in 1990, every measurement was recorded to the nearest millimeter.
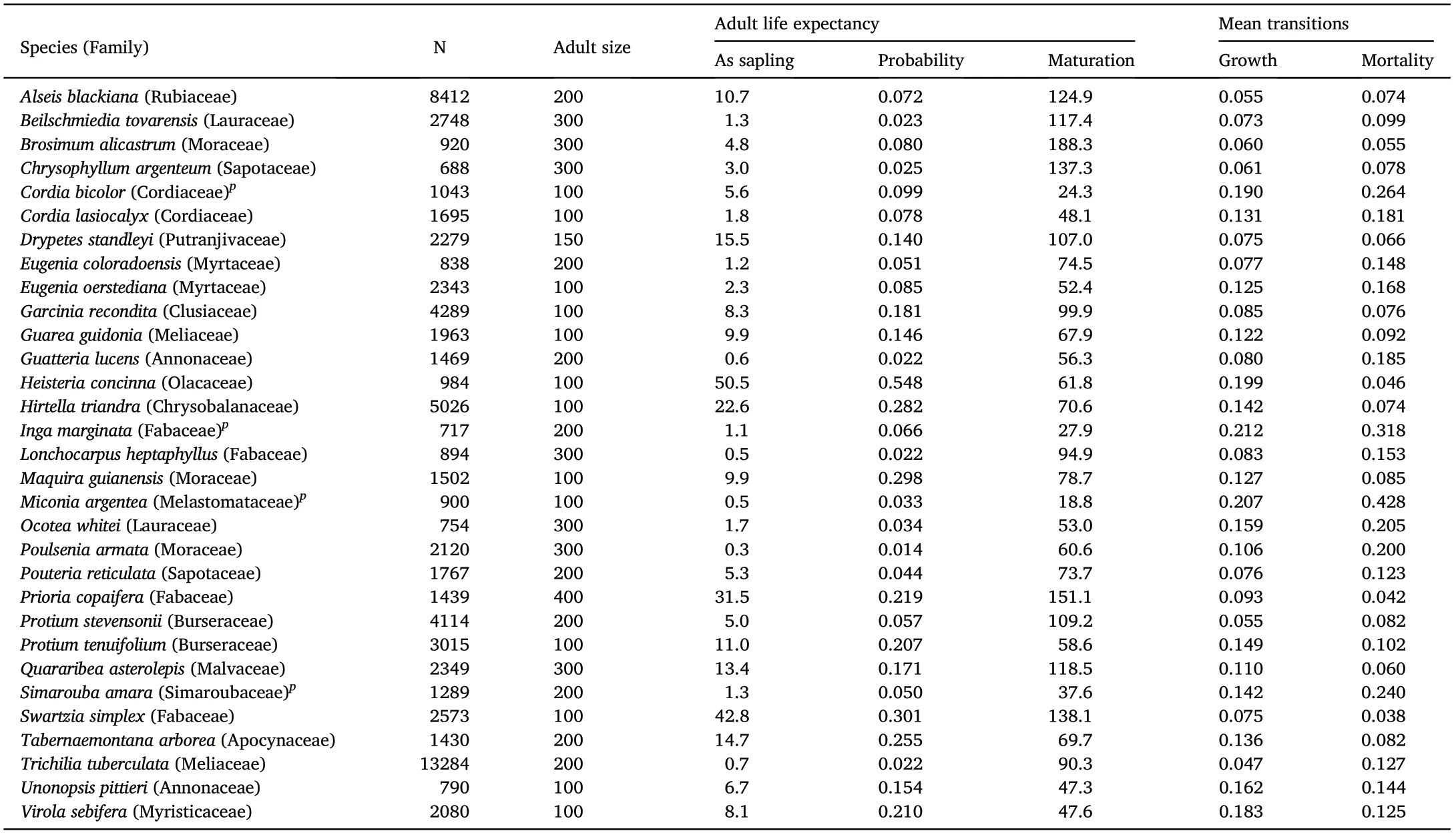
Table 1 The 31 species included in matrix analyses.Adult size is the minimum dbh at which many trees were reproductive.N is total population ≥1 cm dbh in 1990.Adult life expectancy includes the three key demographic traits calculated from transition matrices:1)as sapling is the mean adult life expectancy in years for the average sapling of 1 cm dbh,based on the analytical calculation with two-step growth in pioneers and one step growth in the others;2)probability is the maturation probability,or the probability that a sapling reaches adult size,also based on the analytical solutions;and 3)maturation is the average time in years it takes a sapling to grow from 1 cm to adult size, based on numerical calculations. Mean transitions are the average growth and mortality transitions across all size classes of the transition matrix, i.e. the probability any tree grows to the next size class (or dies) during one 5-year census interval. Pioneer species are indicated with p.
3.2. Species
I analyzed demography for 31 dominant tree species of the 50-ha plot.All had populations of at least 750 trees <10 cm dbh and at least 80 trees≥10 cm dbh in 1990,and had at least one tree measured taller than 16 m(Wright et al., 2010). The abundance criteria were chosen to include several of the fast-growing pioneers (Table 1). The 50-ha plot had 172 species ≥16 m tall in 1990,and the 31 focal species comprised 53%of all individuals of those species.
I estimated adult size from a large dataset of fruit observations in individual trees (Wright et al., 2015; Visser et al., 2016). I defined reproductive size as the first multiple of 50 mm dbh above which many trees were reproductive. Seven species that qualified by the height and abundance criteria were excluded from the study because they reproduced at <50 mm dbh,or had few saplings or few adults.
3.3. Defining size categories
In each species,the largest size class was defined as all trees ≥adult size (Table 1). Juvenile trees were divided into three classes, defined flexibly in order to create near-constant growth transitions. I used an optimization algorithm to adjust two juvenile dbh cutoffs until the three growth transitions were as constant as possible.The resulting dbh classes are roughly logarithmic with respect to dbh, because diameter growth increases as diameter increases. In those species with adult size ≥300 mm dbh, I used four juvenile categories. Appendix 3 gives the size categories.
It is not possible to adjust dbh classes to balance mortality rates. At Barro Colorado,however,mortality declined only slightly from saplings to large trees, from 2.4% to 2.0% (Condit et al., 1995, 2017). The growth-adjusted dbh categories thus lead to matrices whose transition probabilities are reasonably constant. This simplifies theoretical predictions about adult lifespan.
To test the impact of varying size class boundaries, I also created transition matrices in which juveniles were divided into 10 classes of equal width. With adult size = 200 mm dbh, the narrow classes were 21.1 mm wide,so 10–31.1,31.1–52.2 mm,etc.
3.4. Estimating transition matrices
For the 31 selected species,transition matrices were calculated using seven censuses from 1985 to 2015, meaning six different transition matrices,one for each interval of 5 years(I omitted the first interval since it was only 3 years).In each census,all individuals were assigned one of the 4(or 5)size classes based on dbh,and probabilities of death,growth,and residence were calculated as the fraction of trees that moved between classes by the next census. The six transition matrices were then averaged.The transition calculations required several assumptions about stems that broke but survived and stems that shrunk to a smaller size class, detailed in Appendix 4.
Calculating transitions with memory (Eq. 2) from one census pair requires the earlier census as well,since all trees had to be separated into two subclasses depending on the earlier size. This required more assumptions about cases where stems shrunk or broke in one or both intervals (Appendix 4), and only five replicate transition matrices were available.For two-step memory,four consecutive censuses are needed for one transition, reducing the number of replicates to four. Matrices with memory required large samples, since the number of trees in the immediate-growth category was small;matrices with one step of memory were calculated for 28 of 31 species (omitting Brosimum alicastrum,Chrysophyllum argenteum, Lonchocarpus heptaphyllus due to small adult samples), and those with two steps of memory were not calculated for any of the species with adult size of 300 mm(Table 1).The entire set of transition matrices, including all growth steps, with and without memory, are available in digital format in a separate data archive(Condit,2022).
For every matrix, three lifetime demographic statistics were calculated:the expected adult lifespan for saplings(Eqs.3–5),the maturation probability (Eq. 7), and the maturation time (Eq. 8). Every analytical calculation was checked against numerical estimates. Demographic results based on different matrix structures were compared in three ways:1)results from matrices including only one-step growth versus those with two-step growth,2)results from matrices without memory to those with one-or two-step memory(all limited to one-step growth),and 3)results from matrices with 4–5 size classes versus those with 11 size classes(all limited to one-step growth without memory).
3.5. Credible intervals
To estimate statistical confidence in the transition matrices and their demographic results, I estimated Bayesian posterior distributions for all matrix terms. Because transition probabilities are calculated from proportions,it is natural to describe them as binomial variables.This is not quite the case, because they are in fact multinomial, however,binomial probabilities give good approximations to multinomial variables (Fitzpatrick and Alastair, 1987). A posterior distribution of observed transitions was generated with random draws from a binomial distribution using the observed sample size and fraction transiting, using the R function rbinom (R Core Team, 2021). I created 400 random transition matrices for each census interval,then averaged across the six intervals,leading to 400 random matrices.These represent posterior draws of the observed matrix. From each random matrix, all demographic statistics were calculated, and the 5th and 95th percentiles were used as 95%credible intervals.
4. Theory of demographic tradeoff and performance
I compared lifetime demographic performance across the range of growth and mortality rates observed in the 31 species.For each species,I created a simplified matrix with constant transitions across size classes by averaging growth and death transitions, g = gi, m = mi, and calculated the expected adult lifespan from those (Eq. 3). I extended these calculations over an entire demographic space, using Equation 3 with all growth-mortality pairs(g,m) from g= (0.03, 0.04,…,0.24,0.25), m=(0.03,0.04,…,0.49,0.50)i.e.increments of 0.01.Given the lifespan L(g,m) over g-m space, I created a surface with contours showing lines of equal L using the contour function in R (R Core Team, 2021). This theoretical exploration allows the demographic consequences of the growth-mortality tradeoff to be evaluated.If the tradeoff is demographically equalizing, the growth-mortality axis will have constant adult lifespan throughout,i.e.fall on a contour of L.To test this,I estimated a linear correlation between mean g and m probabilities across species,added 95%credible intervals using a Bayesian parameter-fitting method(Condit et al., 2017), then compared expected adult lifespan along the resulting correlation line.
5. Data availability
The entire set of plot data from eight censuses is available in a published archive (Condit et al., 2019). All original transition matrices for the 31 focal species appear in another archive(Condit,2022).
6. Ethics approval and consent to participate
The research involved no human subjects. The forest on Barro Colorado Island is used solely for research purposes under an agreement between the Panama Government and the U.S.Government.
7. Results
7.1. Adult life expectancy of saplings
The expected adult lifespan for the average sapling varied nearly 100-fold in the 31 species,from 0.54 years in the pioneer Miconia argentea to 50.5 years in the shade-tolerant Heisteria concinna(Table 1).Nearly half the species(14 of 31)had expectations <4 years,but several were >10 years and three extremes were >30 years(Fig.1a,Table 1).
Expected adult lifespan was strongly correlated with maturation probability, which varied 40-fold (Fig. 1a), and weakly correlated with maturation time,which varied from 19 to 188 years(Fig.1b).Mortality rate was closely associated with expected adult lifespan (Fig. 2a) but growth rate was not(Fig.2b).

Fig. 1. Maturation probability and maturation time (years) versus expected adult lifespan (years) for the average sapling at 1 cm dbh for 31 dominant tree species in the Barro Colorado 50-ha plot. a)y-axis is the maturation probability for the average sapling.b)y-axis is the maturation time,or mean time(years)it takes the average sapling to reach adult size.Expected adult lifespan is on the xaxis in both panels. Red points mark the four pioneer species, and other species mentioned in the text are labeled as well: pioneers (Cb = Cordia bicolor, Im =Inga marginata, Ma = Miconia argentea, Sa = Simarouba amara); and nonpioneers (Ab = Alseis blackiana, Ba=Brosimum alicastrum, Hc = Heisteria concinna, Ow = Ocotea whitei, Pa=Poulsenia armata, Ss = Swartzia simplex, Tt =Trichilia tuberculata, Up = Unonopsis pittieri). Gray bars, horizontal and vertical,show 95% credible intervals; in a), both are shown, but in b), those for adult lifespan are omitted, since they are identical to a). Curves are based on linear regressions of log-transformed values, but axes are untransformed. In a) the regression is highly significant (p = 3 · 10-12, r2 = 0.82); in b) it is weakly significant (p = 0.034, r2 = 0.15). (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
7.2. The growth-mortality tradeoff and adult life expectancy
The 31 species demonstrated the expected tradeoff between growth and mortality, having high growth significantly associated with high mortality (Fig. 3). The observed tradeoff, however, did not match theoretical contours of equal expected adult lifespan: contours were steeper than the tradeoff (Fig. 3). The mismatch means that traversing the tradeoff axis from low growth and mortality toward high(right along the dashed line in Fig. 3) moves down the ’hill’ of adult lifespan, and that conclusion was supported across credible intervals of the growthmortality trend. For example, two species at opposite extremes, Swartzia simplex and Miconia argentea, are both close to the tradeoff line, but Swartzia had a much longer adult lifespan. At the lowest mortality, the contours were nearly vertical (Fig. 3), thus adult lifespan was nearly independent of growth at low mortality.
7.3. Impact of two-step growth
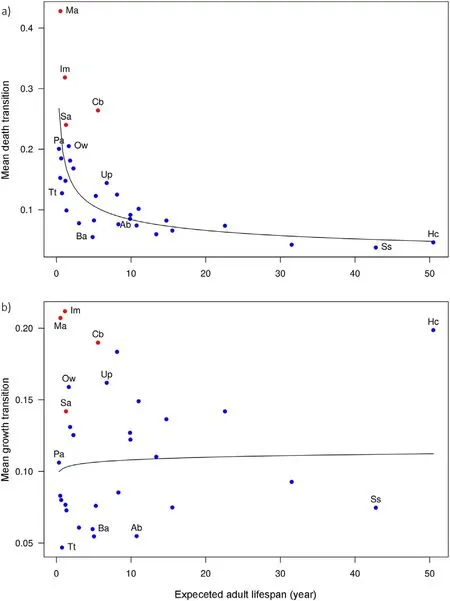
Fig. 2. Growth and death rates versus expected adult lifespan (years) for the average sapling at 1 cm dbh for 31 dominant tree species in the Barro Colorado 50-ha plot. a) y-axis is the mean growth transition across all size classes in the transition matrix, i.e. the probability a tree grows to the next size class in a 5-year census interval. b) y-axis is the mean mortality transition across all size classes, i.e. the probability a tree dies in 5 years. Expected adult lifespan is on the x-axis in both panels. The species labeled match those in Fig. 1. Curves are based on linear regressions of log-transformed values, but axes are untransformed.In a)the regression is highly significant(p=2·10-7,r2=0.61);in b)it is non-significant (p = 0.64, r2 <0.01).

Fig. 3. The observed growth-mortality tradeoff versus theoretical contours of equal expected adult lifespan. Only the 23 species with four-class transition matrices are shown,because the contours differ with the number of size classes.Observed growth and mortality rates are the mean transition probabilities across the four size classes. The central dashed line is the linear regression between observed growth and mortality (statistically significant, p <0.01); the dashed curves above and below it are 95% credible intervals around the regression.Species labels match Figs. 1 and 2.
In most species,matrices with or without two-step growth produced similar demographic outcomes:in 26 of the 31 species,omitting two-step growth reduced the lifespan <10%(i.e.comparing Eqs.3 and 4).In two pioneers, on the other hand (Cordia bicolor, Miconia argentea), many individuals grew by two size classes,and the expected adult lifespan with two-step growth was 90% and 60% higher than without. In three nonpioneers (Ocotea whitei, Poulsenia armata, Unonopsis pittieri), including two-step growth caused a 14–24%increase in adult lifespan.
7.4. Impact of transition with memory
The addition of memory to the transition matrices had minor impacts on estimated demographic outcomes. Expected adult lifespan for a sapling calculated from a matrix with no memory was highly correlated with lifespan based on one- or two-step memory (Fig. 4a). Adding onestep memory to the matrix led to <3% reduction in expected adult lifespan. With two steps of memory, there was a more appreciable change,and adult lifespan was shortened by an average of 20%(Fig.4a).Maturation probability was similarly affected by the addition of memory.Maturation time, however, was nearly unaffected: even with two-step memory,it increased only 3.5%relative to a matrix with no memory.
7.5. Impact of narrow size classes
Redefining size classes to be narrower, and evenly sized, had little impact on the expected adult lifespan of saplings (Fig. 4b). Maturation time and maturation probability were lifewise unaffected by the change in size classes.
8. Discussion
The demographic tradeoff between growth and survival, familiar in forests in general,is not equalizing at Barro Colorado.A growth-survival regression line from 31 abundant species was not parallel to theoretical contours of adult lifespan as expected from the sapling stage.Moving up the regression line, toward higher growth and survival, accompanied a decline in adult lifespan. I conclude that the average pioneer species at Barro Colorado has a shorter adult life expectancy than the average shade-tolerant species. Pioneers have high growth rates, and saplings reach adulthood quickly,however,their death rates are so high that few survive that long.The theoretical contours of equal lifespan demonstrate how the tradeoff could be balancing.Pioneers would need to have lower death rates by a substantial margin. In Cordia bicolor, for example, the observed mean death rate of 28%per 5 years would have to be lowered to 15%for its adult lifespan to reach 4 years,matching that of the very slow growing Alseis blackiana. If reproductive output were similar across the demographic axis, the pioneer group would decline in abundance relative to many of the shade tolerant species.
There was considerable additional variation in adult lifespan around the growth-survival regression. Alseis blackiana and Trichilia tuberculata are conspicuous examples. Both are abundant canopy trees, and both grow slowly, but their expected adult lifespans differed by 12-fold, and Swartzia simplex, another slow-growing species, had an expected adult lifespan another four-fold higher.Assuming similar reproductive output,Trichilia cannot persist.
The contours of equal adult lifespan show that death rate has a greater impact on adult lifespan than does growth, especially at the low end of the growth-mortality axis.Given low mortality,increases in growth have little impact on adult lifespan. This means elasticity of growth is lower than that of survival (Franco and Silvertown, 2004). Selection favoring higher growth rates is thus weak in long-lived forest tree species: traits lowering mortality would have more impact on adult lifespan, and thus reproductive output, than traits raising growth. At the highest growth rates, however, increasing growth and decreasing death have similar impacts on adult lifespan.
These conclusions about sapling to adult lifetimes were robust to key assumptions underlying the matrix method.Adding memory to the transition matrices did not effect the main results,though two-step memory did reduce expected adult lifespan by 20%and increase maturation time slightly.This demonstrates the effect described by Zuidema et al.(2009)whereby a transition matrix can overestimate the fastest growth.That the effect of memory was small supports conclusions of Picard and Liang(2014),who argued that the matrix method also underestimates growth rates at the low end,tending to balance rapid transitions.
One of my goals using matrices with few,broad size classes was to the reduce the impact of growth errors.In previous work,I excluded extreme negative and positive outliers in growth rates. Here, I discounted negative growth by assuming it meant stasis,and I overcame positive errors by omitting two-step growth; in most species, demographic results from one-step growth differed little from those with two-step growth,though in some pioneers, growth by two size classes had to be included. I also checked results from the broad size classes against matrices based on many narrow size classes and found no differences, supporting conclusions in Doak et al. (2021). In general, matrices with only four or five broad classes provided consistent and reliable results on maturation time and expected adult lifespan of saplings. By adjusting size class boundaries, I was able to equalize growth transitions across size classes, an advantage for the theoretical analyses behind the adult lifespan contours.Large sample sizes in abundant species of the 50-ha plot foster the success of my combined empirical-theoretical approach.
Whether the growth-survival tradeoff is equalizing across the entire life cycle remains unknown until reproduction is added to the analysis.Thirty years of data on seed output and germination in the 50-ha plot are available(Wright et al.,2005,2015,2016),and my next goal is build transition matrices that start from seeds. I will then be able to examine expected lifetime reproductive output across the growth-survival tradeoff,and I will examine aspects of demography that account for fluctuations in abundances over the 30 years of observations(Condit et al.,2017).
9. Conclusions
I applied methods from matrix demography to derive lifetime demographic parameters in 31 of the dominant species of a 50-ha forest plot in Panama.Using analytical solutions to matrix projections,I calculated expected adult lifespan for a sapling across a wide range of growth and survival rates. I then estimated the growth-survival regression in those species and overlaid theoretical predictions of adult lifespan across the breadth of demographic variation. Predicted adult lifespan is not constant along the regression line, rather, the upper end of the growthsurvival axis, representing the fast-growing pioneer tree species, had relatively short reproductive lifespan compared to the low end, with shade-tolerant,climax species.This leads to the hypothesis that pioneer species produce more seeds or seedlings while they are reproductive than do climax species.I plan to test this by extending the matrix approach to fruits and seedlings and generate theoretical results on the entire life cycle, from seed to adult and back.
Declaration of competing interest
The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
Stephen Hubbell and Robin Foster designed the 50-ha plot,and Hubbell remains the intellectual driving force. Foster developed the research questions and identified most of the trees. Hubbell’s analyses of Markov matrices for mating theory suggested the matrices with memory.D.Falster,D.Wharton,and T.O’Brien provided insights on the analyses.Numerous grants from National Science Foundation(US),the Smithsonian Institution,the MacArthur Foundation,and Earthwatch supported census work in the Barro Colorado 50-ha plot. The Center for Forest Science at the Morton Arboretum provided support for the author while writing.
Appendices. Supplementary material
Appendices with matrix derivations and supplementary data to this article can be found online at https://doi.org/10.1016/j.fecs.2022.1000 53.
- Forest Ecosystems的其它文章
- Prediction of the global potential geographical distribution of Hylurgus ligniperda using a maximum entropy model
- The 2/3 scaling of twig nitrogen to phosphorus in woody plants
- Monitoring the abundance of saproxylic red-listed species in a managed beech forest by landsat temporal metrics
- Trade-offs among fine-root phosphorus-acquisition strategies of 15 tropical woody species
- Structure complexity is the primary driver of functional diversity in the temperate forests of northeastern China
- Consistent response of nematode communities to management of coniferous plantations

