冲击载荷下周期性多孔夹芯结构拓扑优化及动力响应

廖 芳，李世强，吴桂英

（太原理工大学机械与运载工程学院应用力学研究所, 山西 太原 030024）

由于冲击载荷作用下材料/结构的力学行为是瞬态、大变形、高应变率的强非线性动态过程，其变形和失效不仅涉及几何非线性、材料非线性、接触可变性、不可逆性的边界非线性，还涉及应变强化效应、应变率效应。显著的载荷的时空非线性效应和材料/结构的动力非线性效应令材料/结构的优化问题很难获得设计变量与目标函数之间的显式关系。此外，涉及高度非线性和瞬态动力学的优化问题存在计算成本高、优化效率低、收敛性差和计算不稳定等问题。在优化过程中如何综合考虑冲击载荷的强非线性、结构的几何非线性和材料的非线性效应，是当前拓扑优化领域最具挑战的课题。

多孔材料夹芯结构是一种复合材料夹层结构[1]，通常由2 块金属面层和1 块芯层组成。相比于传统结构，夹芯结构具有高刚度、高强度、能量吸收性能好等优点，被广泛应用于航空航天、建筑、汽车等领域的抗冲击和吸能缓冲结构[2-4]。目前，相关研究主要集中在探索既定拓扑构型夹芯结构（蜂窝、点阵、泡沫、波纹板、仿生多孔材料）的抗冲击性能和能量吸收机制。由于细观变形失效机制与宏观性能之间的内在联系尚不明确，且缺乏以抗冲击性能为目标的动态拓扑优化设计理论体系，实际工程中以结构的抗冲击性能为目标开展夹芯结构细/宏观一体化设计已成为夹芯结构抗冲击设计的前沿基础科学问题。

夹芯结构在冲击载荷作用下的变形模式、响应特征及评价体系是夹芯结构动力学响应研究的热点和难点，也是构建优化问题、建立目标函数及约束条件的基础。夹芯结构的失效模式主要依赖芯层构型、几何参数、结构配置、边界条件、面板与芯层的相互作用、加载方式以及加载率等因素[5]。准静态载荷下，夹芯梁的典型失效模式[6]主要包括上面板褶皱、加载区域芯层剪切、固支端芯层剪切、面板和芯层界面失效、下面板断裂等，夹芯板的失效模式主要有整体弯曲、伴随局部压痕的整体弯曲变形和局部压痕等[7]。冲击载荷作用下，夹芯板的失效模式主要有芯层屈服、冲击面分层、芯层断裂、表皮纤维断裂4 种[8]。这些失效模式之间存在一定的“竞争”关系，最终的变形和失效模式是几种失效模式中所需载荷最小的一种，当2 种或多种失效模式所需载荷相同时，则可能发生模式转化，相关的研究仍有待进一步系统深入地开展。完善多孔材料及其夹芯结构的性能评价体系，并根据工程实际选择合理的评价指标，平衡各指标之间的权重，是建立这类材料的结构优化目标函数和约束条件的前提。多孔材料芯层的性能通常使用总能量吸收（total absorbed energy）、比吸能（specific energy absorption，SEA）、平均承载力（mean force）、压缩力效率（crush force efficiency，CFE）、最大压缩量（maximum compression length）、压缩效率（crush efficiency，CE）、密实化应变（densification strain）等参数进行评估[9-12]。同时，由于需要防护的人员或结构物通常都在夹芯结构的后方，所以夹芯结构的跨中挠度是研究结构抗冲击性能的最重要的参数[13-16]。

针对准静态载荷下材料及结构在线弹性范围内的优化设计，国内外学者开发了众多各具特色的拓扑优化算法，如：变密度法（solid isotropic microstructures with penalization，SIMP）[17]、 渐进优化法（evolutionary structural optimization，ESO）[18]、双向渐进优化法（bi-directional evolutionary structural optimization，BESO）[1-20]、移动变形组件法（moving morphable component，MMC）[21]、特征驱动法（featuredrive method，FM）[22]、水平集方法（level set method，LSM）[23-24]、独立连续映射法（independent continuous and mapping method，ICM）[25]、可行域调整法（feasible domain adjustment method，FDA）[26]等。在冲击载荷下，为了避免非线性因素带来的困难，一类研究是在线弹性静力拓扑优化获得的材料和结构初步优化结果的基础上，通过抗冲击性能分析，校核该优化设计的性能或调整结构设计[27-29]；另一类研究是在拓扑优化设计的过程中首先考虑冲击问题的各类非线性效应，但设计变量更新规则并不是通过数学解析推导获得[30-32]，如PPSS（prescribed plastic strain/stress）法[33]和混合元胞自动机（hybrid cellular automation,HCA）法[34]。Park[35]提出的等效静力（equivalent static loads ，ESL）优化法是一种介于上述两种方法的算法。ESL 法利用构造的等效静力分析代替优化问题中的非线性动力分析以获得优化设计，并采用双层迭代的优化流程更新等效静力分析模型和校核优化设计的非线性动力响应，计算效率高。

本研究从夹芯结构在冲击载荷下的宏观动力响应特性出发，在ESL 框架下基于双向渐进结构优化硬杀法（hard-kill BESO），通过构造双层迭代的混合算法，建立冲击载荷下周期性多孔夹芯结构的拓扑优化方法。在内层迭代中，进行线性静力分析，采用BESO 硬杀法更新设计变量；在外层迭代中，充分利用ABAQUS 商业软件便捷的前处理建模和强大的非线性计算能力，计算结构的动力响应，由此分析优化结构与传统多孔夹芯结构的变形失效机理，并对4 种不同结构（优化夹芯结构、梯形芯夹芯结构、矩形芯夹芯结构和随机Voronoi 芯夹芯结构）的抗冲击性能和吸能特性进行对比。

1 基于BESO 硬杀法的ESL 拓扑优化方法

1.1 基于惯性释放法构造的等效静力载荷

Nelson 等[36]提出惯性释放法以获得冲击载荷下结构响应的近似解。传统的惯性释放法假设结构为刚体，采用刚体动力学理论计算出在外力载荷下不同时刻各个节点的加速度向量，但因免去了非线性动力分析，计算的力学响应精度低。

对于非线性动力问题，控制方程为

式中：M、C和K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵，u¨、u˙和u分别为结构的加速度、速度和位移，f(t)为结构所受的外部载荷。

将惯性力和阻尼力移至等式的右侧，可得以下形式

本研究所关注的非线性瞬态动力学问题中阻尼作用较小，可以省略不计，则

式中：feq(s)为基于改进惯性释放法构造出的等效静力载荷，s为划分的时间步数。与传统的惯性释放法不同，改进惯性释放法中节点的加速度向量是基于非线性动力分析计算得到的，而非刚体假设，因此，其计算结果具有更高的精度。值得注意的是，每个节点都施加了由惯性力和外部载荷作用的等效静载。

1.2 双层迭代优化流程

双层迭代方法的主要思想：在外循环中，开展结构弹塑性非线性动力响应分析，提取q个时刻所有节点的位移响应以构造等效静载；在内循环中，将每个时刻的等效静载作为载荷边界条件对结构进行线性静态分析。于是，基于惯性释放法构造的周期性多孔夹芯结构的优化流程可以描述为6 个步骤（如图1 所示）：(1) 在软件ABAQUS 中分别建立动态有限元模型和静态有限元模型，提取单元和节点信息，设定初始优化参数；(2) 在外循环中，进行非线性动力学分析，考虑载荷和材料的非线性效应，将时域上的力学响应A(t)、f(t)分别离散为q个时刻上的响应A(s)、f(s)，并计算q个时刻的等效静载；(3) 在内循环中，将每一时刻的等效静载作为一个工况下的载荷边界条件，分别写入静态有限元模型中，进行线性静力有限元分析，提取每个工况下优化结构的能量吸收值，相加计算出单元灵敏度；(4) 根据约束条件确定下一步的迭代体积分数，若迭代体积分数满足约束条件则减小体积，反之，则增大体积；(5) 基于步骤(3)计算所得的单元灵敏度更新设计变量xi,j，移除低灵敏度单元，增加高灵敏度单元，并重新构建有限元模型；(6) 重复步骤(2)～步骤(5)，直到满足收敛条件。

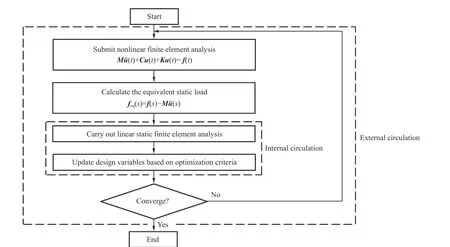
图1 优化流程Fig. 1 Flow chart of topology optimization

2 结构拓扑优化

2.1 性能评价指标

研究夹芯结构在冲击载荷下的能量吸收能力需要考虑以下指标[37]：总能量吸收、比吸能、平均冲击力（mean impact force，MIF），同时夹芯结构上、下面板的跨中最大挠度Ut和Ub也是反映夹芯结构抗冲击性能的重要参数。

总能量吸收EA为刚体冲击过程中夹芯结构因变形吸收的能量，在数值上表示为力-位移（p-x）曲线与x轴围成的面积

对于夹芯结构来说，比吸能和平均冲击力越大，结构的能量吸收性能越好。

2.2 优化问题建模

当前，结构轻质化是结构研发的一个热门趋势，在保证结构性能满足要求的同时，减小结构质量是促进航空航天发展的方法之一。对于大多数夹芯结构来说，塑性变形越大，结构的总体能量吸收性能越优异。但在实际工程应用中，为减小冲击载荷对结构和人的伤害，需保证结构的跨中最大挠度在合理范围内，然而这会导致吸收能量减少。保证挠度在一定范围内的前提下获得能量吸收性能最好、体积分数最小的结构，是吸能缓冲结构设计的主要目标。为此，本研究以能量吸收最大化、体积最小化为目标函数，最大位移不大于许用最大位移为约束条件。

夹芯结构呈周期性，芯层被划分为m=m1×m2个胞元，其中，m1和m2分别为沿x和y方向的单胞个数，如图2 所示。

图2 典型的具有m1× m2 个单胞的二维周期结构Fig. 2 Representative two dimensional periodic structure with m1× m2 cells

设计变量为xi,j（0 或1），i和j分别为胞元编号和单元编号，其中单元编号为夹芯结构单个胞元中单元的编号。优化问题可以表述为

式中：N为选择的迭代步数，τ 为允许收敛误差。在本研究中N和τ 分别取为4 和0.1%，则式(12)表示为前4 步迭代和后4 步迭代体积分数的改变量不超过0.1%，即在最近8 次迭代中，体积分数的变化非常小，趋于平稳。

2.3 优化结果

图3 为夹芯梁受刚体冲击的示意图，结构的左右两端均受固支约束。刚体和结构的尺寸分别为12 mm×10 mm 和180 mm×38 mm，结构上下端各有1 mm 厚的面板（作为非设计域），面板中间为36 mm 厚的芯层（作为设计域），刚体的冲击速度为100 m/s。优化算法对材料属性无特殊要求，面板和芯层均采用常见的双线性弹塑性材料模型。面板采用经退火处理的304 不锈钢[39]，密度ρ1=7 930 kg/m3，弹性模量E1E=193 GPa，泊松比ν1=0.3，屈服强度 σ10=241 MPa，切线模量EP1=19.3 GPa。芯层采用铝合金[40]，密度ρ2=2 680 kg/m3，弹性模量E2E=70 GPa，泊松比ν2=0.3，屈服强度 σ20=325 MPa，极限强度σUTS=340 MPa，对应的应变εUTS=0.14。将优化结构划分为m=10×2 个胞元，约束条件为下面板的跨中挠度不大于15 mm。

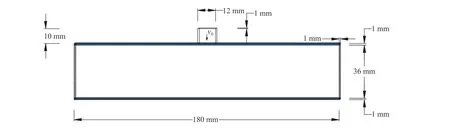
图3 冲击载荷下固支梁结构示意图Fig. 3 Schematic diagram of fixed sandwich structure subjected to impact load

图4(a)为固支夹芯结构在拓扑优化过程中的体积分数Vf、下面板的跨中位移Ub和结构吸能EA的演变历程。图4(a)显示，随着结构体积的不断减小，受到相同载荷冲击时，在约束范围内变形不断增大，更多单元进入塑性阶段，结构吸收的能量不断增加，结构最终的体积分数为47.22%。其中，迭代至第10、20、30、40 和50 步时的拓扑构型如图4(b)所示。可以看出，每个胞元材料都分布清晰，且优化结构具有很好的周期性。在迭代至第39 步时，夹芯结构的下面板挠度小于约束值，优化进入收敛阶段，在迭代至第51 步时，夹芯结构同时满足约束条件和收敛条件。

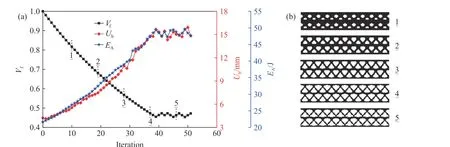
图4 固支夹芯结构优化历程Fig. 4 Evolutionary histories of fixed-clamped sandwich structure

3 结果分析

3.1 结构设计

本研究设计了4 种不同几何构型的夹芯梁（夹芯梁由面板和芯层组成）。4 种几何构型中，面板的长度、宽度均分别为180 和1 mm（见图5(a)），芯层单元分别为优化芯层、梯形波纹芯、矩形波纹芯和随机Voronoi 芯层。优化芯层采用2.3 节固支梁拓扑优化所得结果。梯形芯层（见图5(b)）的高度H1为17.5 mm，芯层厚度t1为3.5 mm，厚度t2为1.5 mm，底角θ 为76°。矩形芯层（见图5(c)）的高度H2为17.5 mm，芯层厚度t3为3.5 mm，厚度t4为2.95 mm，厚度t5为1.5 mm。生成的随机Voronoi 芯层的参数为：宽度W为180 mm，高度H3为36 mm，胞元最小距离dmin为0.1 mm，胞元数量m为100，厚度t6为2.2 mm。优化芯层夹芯板、波纹夹芯板由多层面板和波纹芯层组成，随机Voronoi 芯层夹芯板由上下面板和Voronoi 芯层组成，图6 为其结构示意图。4 种结构的质量相同，材料参数与2.3 节中所列数据的相同。

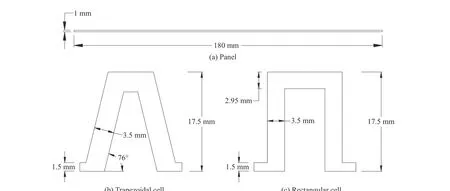
图5 芯层和面板的结构参数Fig. 5 Structural parameters of core and panel

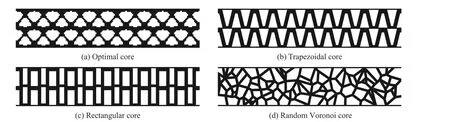
图6 不同芯层的夹芯结构示意图Fig. 6 Schematic diagram of sandwich structures with different cores

3.2 模拟结果与分析

采用ABAQUS 有限元软件分析了优化夹芯结构、双层波纹芯夹芯结构和随机Voronoi 芯夹芯结构在刚体冲击下的变形模式。面板和芯层材料的参数与2.3 节一致。刚体冲击下夹芯结构的有限元模型主要包括2 个部分：刚体和夹芯结构。刚体长度为12 mm，厚度为10 mm。刚体和夹芯结构均采用八节点实体单元（C3D8R）描述。刚体的初始速度v0=100 m/s。夹芯结构两端固定，面板与芯层之间采用绑定约束。

图7 为4 种夹芯结构在100 m/s 的刚体冲击下的变形模式。图8 为冲击载荷下4 种夹芯结构的吸能曲线。结合图7 和图8 可以看出，当t=0.3 ms 时，优化夹芯结构第1 芯层的刚体撞击区域被完全压缩，波纹芯夹芯结构发生弯曲，随机Voronoi 芯夹芯结构部分杆件被压缩，此时优化夹芯结构的能量吸收是4 种结构中最大的；当t=0.6 ms 时，刚体继续向下压缩结构，优化夹芯结构的能量吸收依然保持最大，但与其他3 种结构的能量吸收差距减小；当t=0.9 ms 时，刚体反弹离开优化夹芯结构，此时优化夹芯结构只受自身惯性力和阻尼力的作用，不再受外部载荷作用，不发生额外的塑性变形，能量吸收未出现较大的增加，而其他3 种结构仍处于刚体的冲击作用下；当t=1.2 ms 时，刚体与矩形芯夹芯结构和随机Voronoi 芯夹芯结构的面板分离；当t=1.5 ms 时，刚体与梯形芯夹芯结构的面板分离，优化夹芯结构、梯形芯夹芯结构、矩形芯夹芯结构和随机Voronoi 芯夹芯结构的能量吸收值分别为43.751、44.571、52.832 和41.579 J；之后，所有夹芯结构均在平衡位置上下振荡直至稳定。梯形芯夹芯结构上下面板的挠度较大，优化夹芯结构和随机Voronoi 芯夹芯结构的变形较小。优化夹芯结构和随机Voronoi 芯夹芯结构均有部分区域出现压缩密实化现象，而波纹芯夹芯结构只在左右侧肋处发生弯曲。由能量守恒定律可知，较大的塑性变形会使结构的能量耗散增加，变形越大的结构拥有更高的能量耗散。虽然优化夹芯结构的总能量吸收较小，但也拥有最小的变形，实现了能量吸收与变形之间的平衡。

图7 不同夹芯结构的变形模式Fig. 7 Deformation modes of different sandwich structures

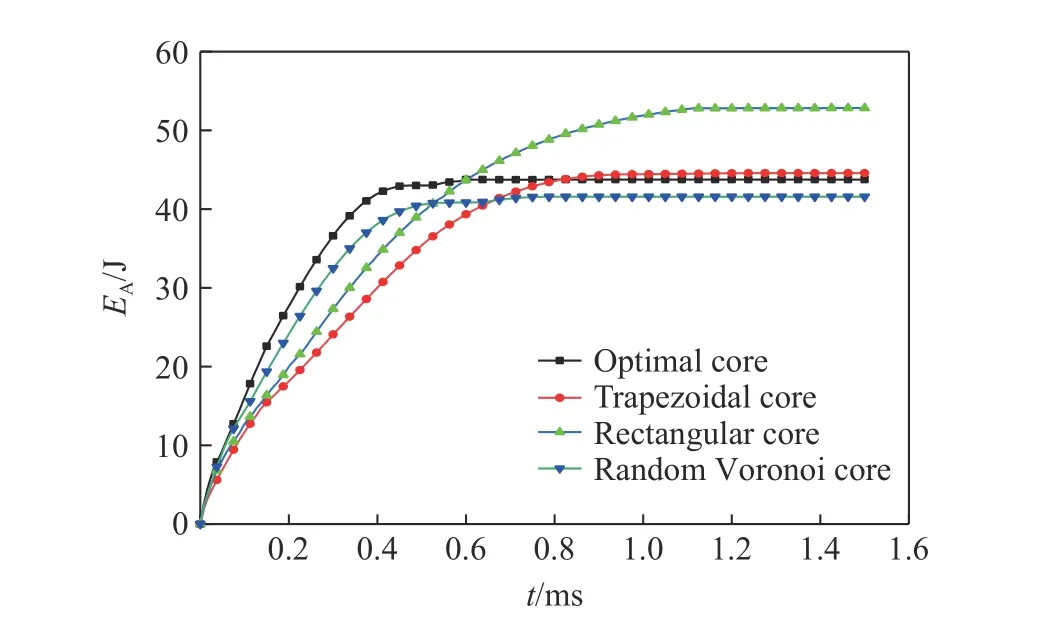
图8 冲击载荷下不同夹芯结构的吸能时程曲线Fig. 8 Energy absorption of differnet sandwich structures versus time under impact load

考虑到结构在实际应用时载荷工况的不确定性，对上述4 种夹芯结构在1～150 m/s 的刚体冲击下的力学性能进行分析。图9(a)、图9(b)分别为夹芯结构上、下面板的跨中挠度随刚体初始速度的变化曲线。在刚体初始速度不断变化的过程中，优化夹芯结构的上下面板的跨中挠度始终是4 种结构中最小的。当速度低于10 m/s 时，4 种结构的跨中挠度相差较小。表1 和表2 为刚体初始速度不小于30 m/s 时优化结构上、下面板的跨中挠度（、）与其他3 种结构中跨中挠度的最大值（Ut,max、Ub,max）的对比。可以看出：对于上面板，当刚体的初始速度为100 m/s 时，除优化结构外的3 种其他结构中，梯形芯夹芯结构的跨中挠度最大，此时，优化结构的跨中挠度与梯形波纹芯的跨中挠度相比，减小幅值最大，减小了34.7%；对于下面板，当刚体的初始速度为100 m/s 时，除优化结构外的3 种其他结构中，梯形波纹芯的跨中挠度依旧最大，优化结构的跨中挠度与梯形波纹芯的跨中挠度相比，减小了51.5%；对于下面板，当刚体的初始速度为30 m/s 时，除优化结构外的3 种其他结构中，矩形波纹芯的跨中挠度最大，此时，优化结构的跨中挠度与矩形波纹芯的跨中挠度相比，减小幅值最大，减小了73.9%。

表1 优化结构的上面板挠度与其他3 种结构中上面板挠度的最大值的对比Table 1 Comparison of top panel deflection of optimal structure and the maximum value of other three structures

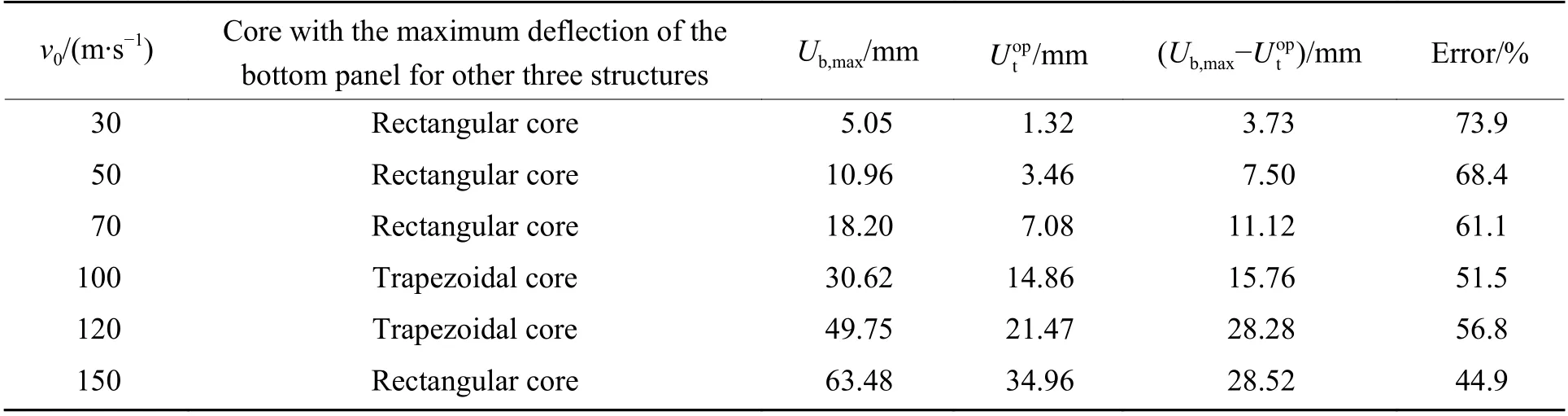
表2 优化结构的下面板挠度与其他3 种结构中最大值的对比Table 2 Comparison of bottom panel deflection of optimal structure and the maximum value of other three structures

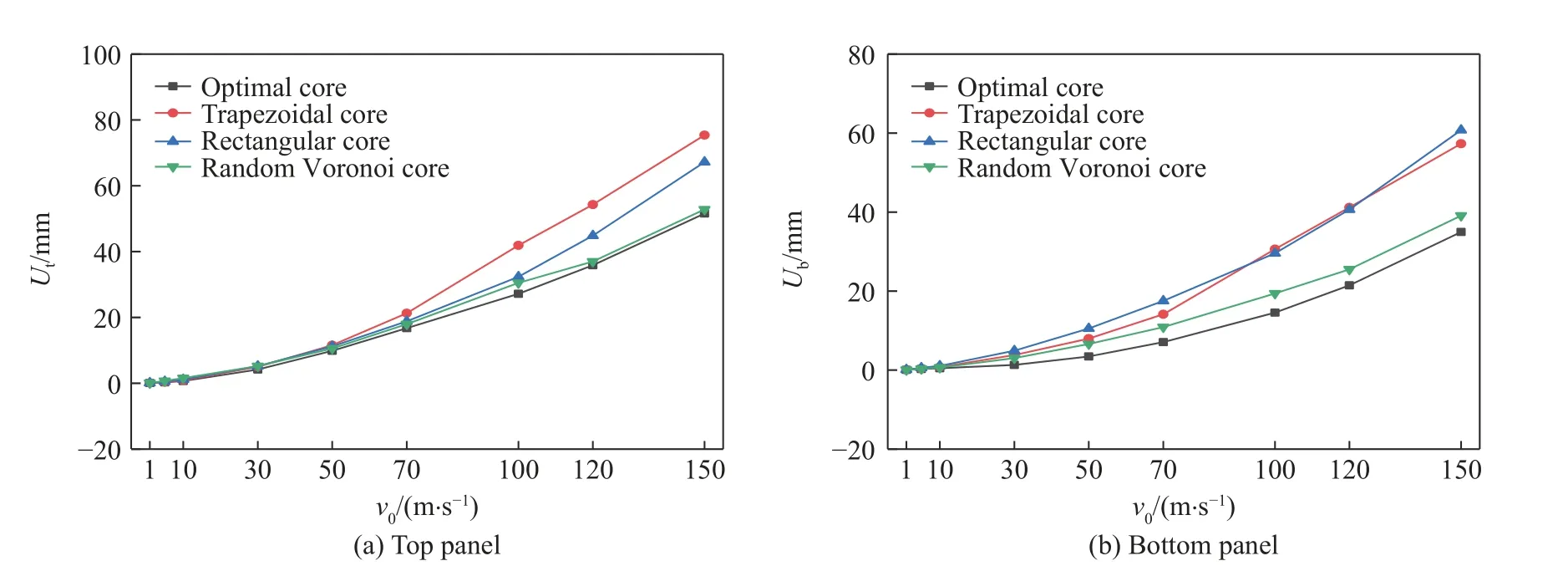
图9 不同速度的刚体撞击下不同结构上下面板的跨中挠度Fig. 9 Deflections at the center points of top and bottom panels of different sandwich structures under the rigid body impact at different velocities

图10(a)给出了夹芯结构的比吸能。当刚体的初始速度为1 m/s 时，4 种结构在冲击载荷下均处于弹性阶段，未发生塑性变形。当刚体的初始速度从5 m/s 提升至30 m/s 时，4 种夹芯结构的比吸能性能差异不大。当刚体的初始速度从50 m/s 提升至120 m/s 时，优化夹芯结构的比吸能高于随机Voronoi 芯夹芯结构，但与其他两种结构相比，其比吸能较小。当刚体的初始速度为150 m/s 时，优化夹芯结构的比吸能为4 种夹芯结构中最高的。图10(b)给出了不同速度的刚体冲击下芯层能量耗散EC与整个夹芯结构能量耗散EW之比（即芯层吸能占比，EC/EW），在所研究的速度范围内，优化夹芯结构的芯层都具有更高的吸能占比，因此，优化夹芯结构中材料的空间分布是4 种结构中最佳的。

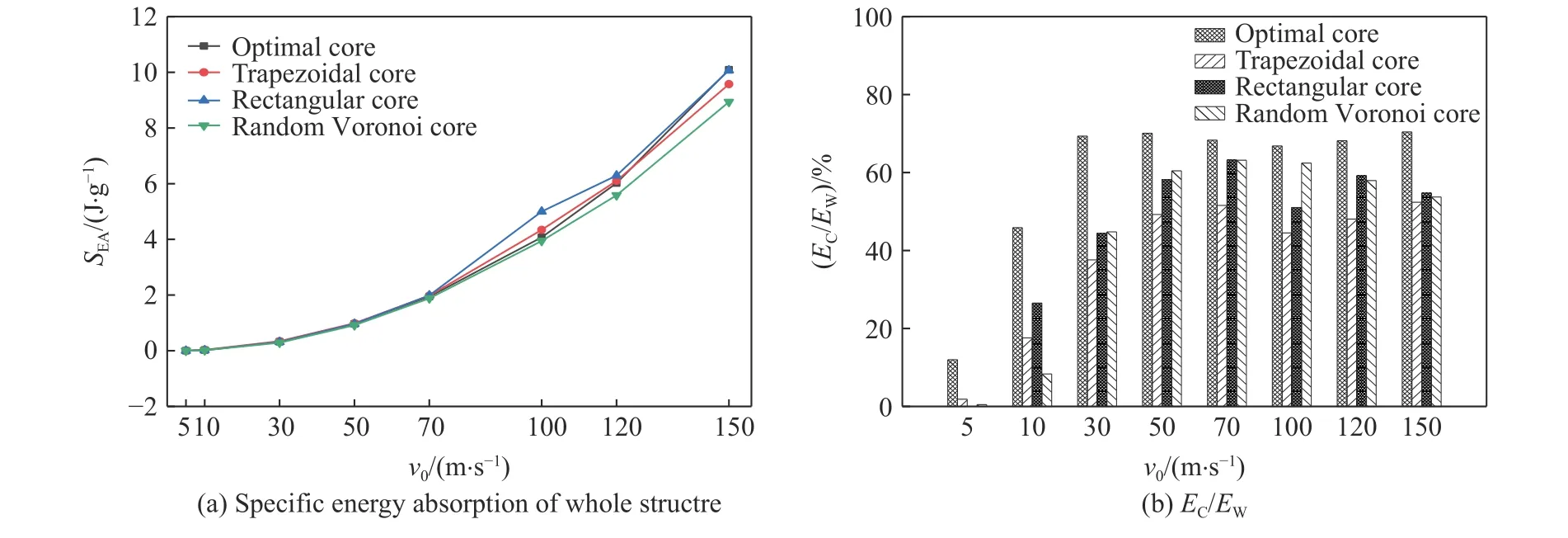
图10 不同速度的刚体撞击下夹芯结构的比吸能和芯层吸能占比EC/EWFig. 10 Comparison of specific energy absorption and EC/EW of sandwich structures under the rigid body impact at different velocities

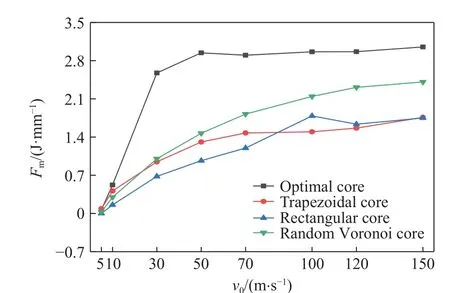
图11 比较了4 种夹芯结构在不同速度的刚体冲击下受到的平均冲击力。在速度为5 m/s 时，优化夹芯结构由于能量吸收较少，受到的平均冲击力小于梯形芯夹芯结构，未能完全体现出结构优化的优势。当速度从10 m/s 升至150 m/s 时，优化夹芯结构受到的平均冲击力是4 种夹芯结构中最大的，充分显示了其吸能缓冲性能。对于一个吸能结构来说，比吸能、芯层吸能占比和平均冲击力越大，结构的吸能特性越好。吸能结构利用材料的塑性变形吸收冲击能量，但需要外层结构的动态响应处于弹性范围内。综合考虑上下面板的跨中挠度、比吸能、芯层吸能占比和平均冲击力5 种性能，优化夹芯结构具有更加优异的能量吸收性能和抗冲击能力，尤其是在高速冲击载荷下，优化夹芯结构的5 种性能均比上述提及的传统波纹芯夹芯结构和随机Voronoi芯夹芯结构更好。

4 不同类型载荷下夹芯结构性能比较

4.1 载荷定义

为了研究不同载荷对结构性能的影响，定义了随时间、空间变化的3 种不同类型的脉冲载荷，分别为矩形脉冲、三角脉冲和指数脉冲。

式中：τ=0.02 ms。

4.2 响应分析

将矩形脉冲、三角脉冲和指数脉冲分别作用于优化夹芯结构、梯形芯夹芯结构、矩形芯夹芯结构和随机Voronoi 芯夹芯结构，4 种结构在3 种脉冲下的最终变形结果如图12 所示。在变形过程中优化夹芯结构的芯层压缩较为严重，梯形芯夹芯结构单侧侧肋发生弯曲，矩形芯夹芯结构两侧侧肋均发生弯曲，随机Voronoi 芯夹芯结构的部分杆件发生压缩屈曲。从图12 可以看出，相较于随机Voronoi 芯夹芯结构，优化夹芯结构的面板变形较小，这与芯层在总能量吸收中的占比有直接关联。

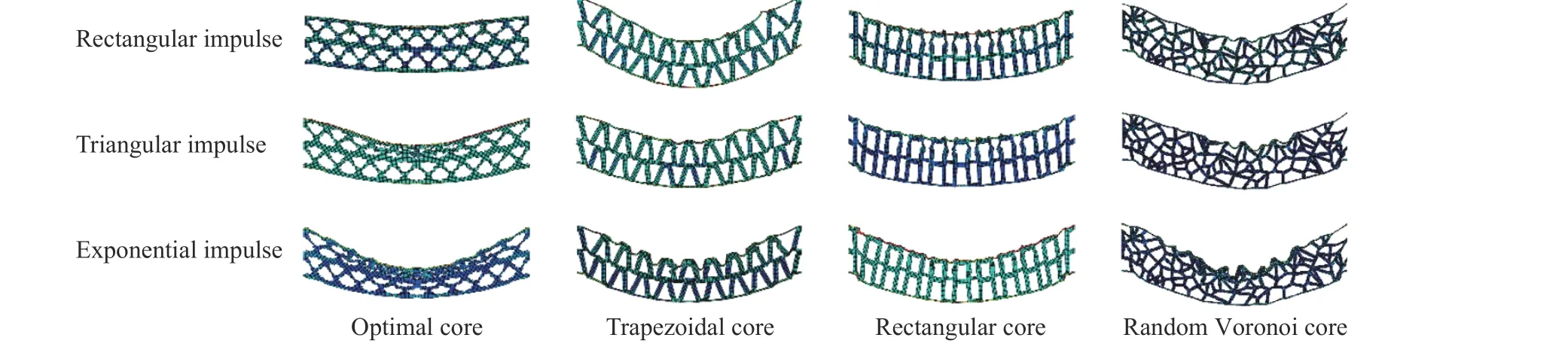
图12 不同脉冲下夹芯结构的变形Fig. 12 Deformations of sandwich structures under different impulse loads

图13 给出了3 种脉冲下夹芯结构上下面板的跨中最大挠度。指数脉冲下，优化夹芯结构上面板的跨中挠度大于梯形芯夹芯结构和矩形芯夹芯结构，相对增量分别为1.36%和5.46%；矩形脉冲和三角脉冲下，优化夹芯结构的上面板跨中挠度最小。3 种载荷下，优化夹芯结构下面板的跨中挠度是4 种结构中最小的，尤其在矩形脉冲下，其与梯形芯、矩形芯和随机Voronoi 芯夹芯结构下面板的跨中挠度的差距更大，相对减小量分别为78.70%、62.96%和73.74%。

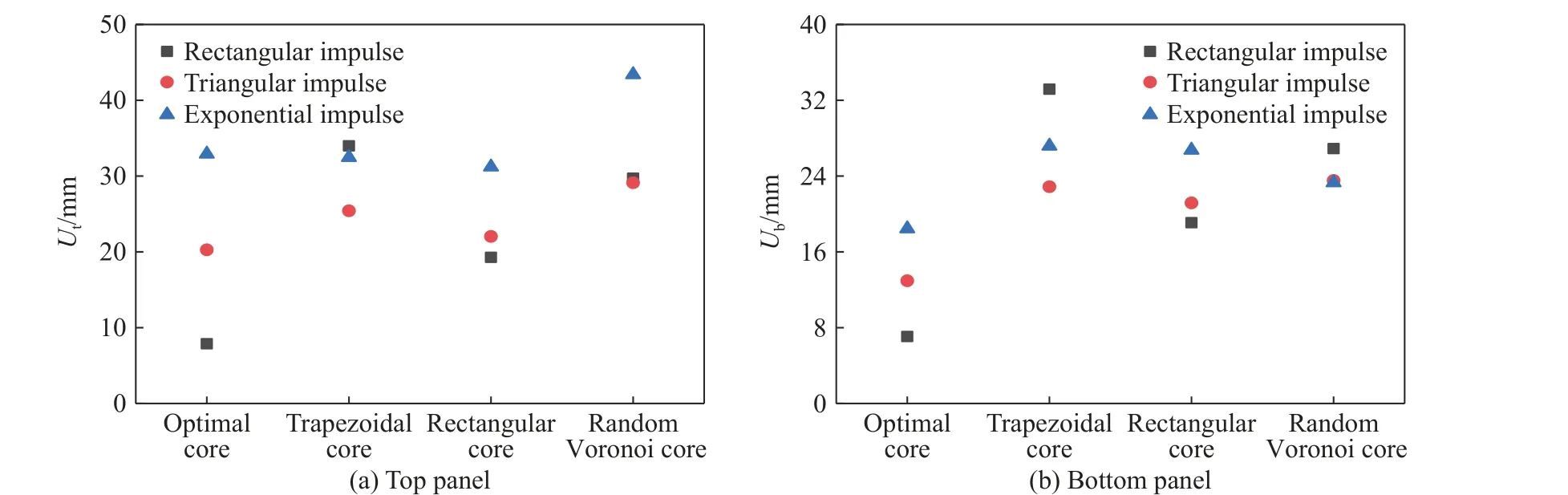
图13 不同脉冲下不同夹芯结构上下面板的跨中挠度Fig. 13 Deflections at the center points of top and bottom panels of sandwich structures under different impulse loads

图14(a)比较了4 种夹芯结构的比吸能特性。在矩形脉冲下，优化夹芯结构的比吸能比矩形芯夹芯结构小33.89%。在三角脉冲和指数脉冲下，优化夹芯结构的比吸能最大。其中，在三角脉冲下，优化夹芯结构的比吸能与梯形芯、矩形芯和随机Voronoi 芯夹芯结构的比吸能差距最大，相对增加量分别为136.28%、30.74%和1 004.20%。图14(b)、图14(c)和图14(d)比较了不同脉冲下各面层与整个夹芯结构能量耗散之比（即面层吸能占比），可以看出在3 种脉冲下，优化夹芯结构的芯层吸能占比最高，其面板吸能占比最低，说明优化结构具有更加优异的材料空间分布，在受到冲击作用时，芯层能够更充分地发挥其能量吸收能力。

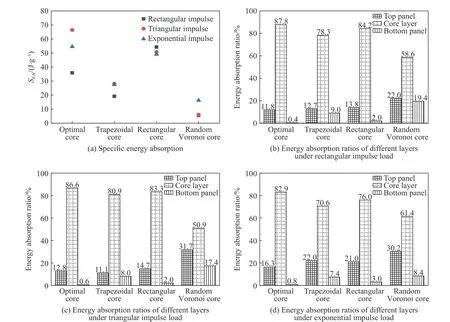
图14 不同脉冲下夹芯结构的吸能性能比较Fig. 14 Comparison of energy absorption of sandwich structures under different impulse loads

5 结 论

在ESL 方法框架下基于BESO 构建了冲击载荷下周期性多孔夹芯结构的拓扑优化方法。在冲击载荷下，以能量吸收最大、体积分数最小为优化目标，以下面板的跨中挠度不大于15 mm 为约束，实现了周期性多孔夹芯结构的拓扑优化。对优化夹芯结构与梯形芯夹芯结构、矩形芯夹芯结构和随机Voronoi 芯夹芯结构开展了不同速度的刚体撞击下、不同脉冲载荷作用下的数值模拟，定量分析了4 种结构的上下面板的跨中挠度、比吸能、芯层吸能占比和平均冲击力，得到以下结论。

(1) 通过分析4 种结构在不同速度的刚体冲击下的变形失效模式可知，在载荷作用前期，优化夹芯结构的受载区域芯层被压缩密实化，随机Voronoi 芯夹芯结构的部分杆件被压缩，而传统波纹芯夹芯结构只发生侧肋弯曲。因此，载荷作用前期，优化夹芯结构的能量吸收值是4 种结构中最高的；在载荷作用后期，优化夹芯结构由于塑性变形最小，其最终的能量吸收值小于波纹芯夹芯结构。

(2) 综合考虑上下面板的跨中挠度、比吸能、芯层吸能占比和平均冲击力5 种特性后发现，在刚体撞击下，相较于梯形芯夹芯结构、矩形芯夹芯结构和随机Voronoi 芯夹芯结构，优化夹芯结构具有更好的能量吸收性能。在刚体速度为150 m/s 时，优化夹芯结构的5 种性能均优于其他3 种夹芯结构。

(3) 通过比较优化夹芯结构、梯形芯夹芯结构、矩形芯夹芯结构和随机Voronoi 芯夹芯结构在矩形脉冲、三角脉冲和指数脉冲下的变形失效模式和力学性能，进一步确定了结构优化的应用范围。在指数脉冲下，优化夹芯结构上面板的跨中挠度大于波纹芯夹芯结构；在矩形脉冲下，优化夹芯结构的比吸能小于矩形芯夹芯结构，未能体现出结构优化的优势；在三角脉冲下，优化夹芯结构的性能均优于其他3 种结构。这说明单一工况下优化所得的夹芯结构不能在任意载荷下均表现出较好的性能，因而，针对不同的载荷工况需要开展进一步研究。