神经系统疾病与认知动力学 (I) :癫痫发作的动力学与控制

韩 芳 樊登贵 张丽媛 王青云

1 东华大学信息科学与技术学院, 上海 201620 2 北京科技大学数理学院, 北京 100083

3 北京工业大学环境与生命学部, 北京 100124

4 北京航空航天大学航空科学与工程学院, 北京 100191

1 引 言

癫痫是由中枢神经系统功能活动异常诱发, 是最常见的慢性神经系统疾病之一. 据世界卫生组织报道, 全球约有6500 万癫痫患者, 我国癫痫患者人数近千万 (Guekht et al. 2021) . 癫痫反复发作会造成患者脑神经元损害, 引起记忆力下降、智力和精神障碍, 严重损害身心健康, 带来巨大的家庭和社会负担. 因此, 对癫痫疾病的预防、早期诊断、早期干预和治疗的研究尤为紧迫.然而, 癫痫的病理非常复杂, 弄清该疾病发生发展的神经机制仍是神经科学领域的难点问题.

脑神经网络活动呈现高度的复杂动态行为, 静息态功能性磁共振 (functional magnetic resonance imaging, fMRI) 联合脑电图 (Electroencephalogram, EEG) 检测发现癫痫患者发作期的脑功能网络与发作间期相比存在广泛的结构连接异常, 紧密关联于癫痫发作的严重程度 (Sharma et al. 2019, Markoula et al. 2018, Centeno et al. 2014) . 采用弥散张量成像的研究也揭示了癫痫患者额颞叶脑结构网络异常与脑功能之间的因果关系 (Liao et al. 2011, Leyden et al. 2015). 然而脑结构功能网络异常在癫痫发展中的特征和规律及其调控机制尚缺乏系统性的研究. 只有成功解析产生各种癫痫病态功能的神经环路的运行规则, 才能真正理解癫痫脑神经疾病的发作机理, 预测癫痫的时空动态演化趋势和病灶溯源, 并制定行之有效的癫痫调控策略.

海马环路证实与癫痫发作相关 (Blümcke et al. 2013, Fröhlich 2016) , 如颞叶癫痫等. 脑皮质是各类癫痫的主要病灶所在 (Kramer & Cash 2012, Matsumoto et al. 1964) , 而皮下结构通过不同方式参与到不同形式的全面性和部分性癫痫发作中 (Badawy et al. 2013, Verghese et al. 2014) , 如皮质下丘脑 (Guye et al. 2006, Burdette et al. 2020) 和基底节 (Slaght et al. 2002, Rektor et al. 2012,Pizzo et al. 2021) 分别对皮质癫痫发作起着类似起搏器的驱动作用和调节作用. 事实上, 这些环路紧密关联于癫痫等各种神经系统疾病的发作和控制, 是神经信息传播和整合的重要功能支撑,对执行脑神经网络动态行为的调控具有关键作用 (Paz et al. 2015, Sporns et al. 2004, Womelsdorf et al. 2014, He et al. 2020, Gong et al. 2021, Zhang et al. 2021) . 如临床深脑电刺激 (deep brain stimulation, DBS) 治疗癫痫被认为是通过刺激脑内特定的神经环路来控制癫痫发作.

实验和临床证据表明癫痫发作过程与神经系统本身的非线性动力学行为密切相关. 然而长期以来, 人们对癫痫电生理现象的研究主要依靠实验结果的直观理解, 缺乏全面深入的规律性认识. 二十世纪八九十年代以后, 国内外计算神经科学领域的学者们开始关注具体神经疾病相关的非线性理论模型及其动力学行为等科学问题的研究, 并逐渐认识到癫痫与大脑神经系统动力学演化密切关联 (Mackey & Milton 1987, Lopes da Silva et al. 1994, Milton & Black 1995) .为此基于癫痫临床电生理实验, 借助数学、物理学和计算机技术等建立了丰富的非线性动力学模型, 以便能深入理解神经疾病发作的动力学本质, 寻求有效的非线性控制手段和治疗方案. 因此, 癫痫脑疾病的研究首先是实现对致痫网络神经元集群病态活动的实时观察, 获得特定神经环路的结构形态及其功能活动模式, 并将现代非线性动力学发展的方法应用于实验数据分析建立科学合理的时空网络动力学模型, 准确演化特定癫痫患者的病态生理特征, 分析出癫痫发生发展的动力学机理, 从而实现癫痫数据统计建模与动力学机理建模的有效融合. 目前, 构建癫痫数据驱动的统计建模与动力学机理建模相互融合的新框架, 已经成为癫痫发作机制研究的潜在途径.

基于动力学计算模型的癫痫研究从各个层次 (包括微观的分子、神经元和胶质细胞水平到宏观的神经元群以及大尺度全脑网络等) 深化了人们对癫痫的认识 (Wendling et al. 2016) .这些不同层次的癫痫计算模型主要包括神经元网络模型 (Tort et al. 2008, Zhang et al. 2017) 、基于统计物理发展的对神经元集群整体行为进行建模的平均场模型 (Chen et al. 2014, 2015; Breakspear et al. 2006) , 以及由平均场技术演化的神经场模型和神经元群模型 (Wendling et al. 2002, 2016;Taylor & Baier 2011) 等. 神经元网络模型能够更加真实地模拟癫痫的网络发作特征 (Beverlin et al. 2012, Beverlin & Netoff 2013). 最新实验研究表明胶质细胞同样能感知外界刺激, 其反应选择性甚至高于相邻神经元, 因此胶质细胞如何参与调控癫痫发作成为近几年研究的焦点问题 (Du et al. 2018, Li & Wang 2016, Li & Tang 2016). 但对于非线性动力学来说, 将大脑视为神经元和胶质细胞整体的组成来研究癫痫是一个具有挑战性的课题, 因为神经元网络模型涉及高维复杂时滞动力系统, 对理论分析和计算成本提出极大挑战. 场模型主要通过统计学手段降低模型中系统的变量自由度, 来用较少变量反应系统的变化特征, 从而降低计算的时间复杂度. 特别地, 场模型参数仍能够考虑大脑真实环境的各种因素如信息传递延迟和突触活性产生的噪声等, 并且可以模拟出神经集群活动的稳态放电率、诱发响应电位、皮层不同频段脑电活动、脑电时空相干性等.基于上述动力学模型, 学者们开展了大量关于癫痫发作动力学机制的研究, 如癫痫的间歇性自发发作转迁的动力学机制 (Goodfellow et al. 2011) 和分岔机制 (Suffczynski et al. 2004, Baier et al. 2012) 等.

癫痫疾病的治疗手段主要有抗癫痫药物治疗、病灶切除以及深脑电刺激等. 关于电刺激控制癫痫疾病的病态特性已经开展了广泛的研究. 大量的电生理实验和临床证据表明特定的电刺激能够成功地控制或终止癫痫发作 (Nelson et al. 2011, Boon et al. 2007). 尽管如此, 电刺激控制癫痫的动力学机理尚未清楚. 基于神经电生理实验从神经系统建模角度, 学者们已对癫痫神经刺激调控的干扰机制进行了相关的研究, 如随机干扰刺激如何诱发和终止癫痫失神发作 (Fan &Liu 2016, Taylor et al. 2014) 、深脑刺激的刺激频率对癫痫神经调控的影响 (Toprani et al. 2013,Schiller & Bankirer 2007) 和电刺激癫痫的最优控制参数如何选择等 (Berényi et al. 2012, Taylor et al. 2015, Salem et al. 2016, Su et al. 2008, Arrais et al. 2021) . 然而, 由于癫痫病理本身的复杂性,使得针对癫痫的建模分析异常困难, 理论与实验研究仍没有很好地揭示癫痫网络刺激响应的动力学机制, 基于发病机制研究预防和控制癫痫发作的方案依旧匮乏.另一方面, 目前对癫痫发作转迁的动力学机理还缺乏统一的认识, 不同癫痫状态发作转迁的路径、癫痫发作与睡眠状态的相互转迁动力学机制、时滞对癫痫发作转迁动力学的影响等都没有从动力学角度研究清楚.另外, 数据驱动的临床癫痫病灶精确定位和控制癫痫网络的关键节点选择等都还缺乏有效策略, 局灶性癫痫发作传播及其控制仍缺乏动力学的理解. 本文的工作分别针对这些问题进行了细致而深刻的研究, 建立了一个完善的皮质-基底节-丘脑环路网络动力学理论框架, 为深入研究癫痫多尺度跨层次网络动力学行为及其调控策略设计提供了重要的理论思路.

本文将首先介绍癫痫神经疾病动力学与控制方面的研究进展, 并分别给出本文作者在颞叶癫痫、局灶性癫痫和失神癫痫等发作转迁动力学建模分析及其调控方面的最新研究成果.具体地, 本文第2 节主要讨论颞叶癫痫海马神经元网络动力学建模分析与调控; 第3 节基于神经场模型方法分析了癫痫发作的皮质-丘脑环路动力学机制; 第4 节基于平均场的建模方法构建了皮质-基底节-丘脑环路网络动力学模型, 主要揭示电刺激调控癫痫发作的动力学机理; 第5 节基于癫痫数据驱动利用神经元群网络动力学模型对局灶性癫痫的病灶定位及其网络调控进行建模分析.

2 癫痫神经元网络动力学建模分析与调控

2.1 基于海马DG-CA3 网络的颞叶癫痫转迁动力学建模分析

颞叶癫痫起始于颞叶, 是一种经直接通路或间接通路首先传播到颞叶结构的局灶性癫痫. 海马结构易损伤, 从而诱发癫痫. 基本的海马环路从齿状回 (dentate gyrus, DG) 区开始, 沿S 形弧线工作, 将信息传递至CA3 区, 再传递至CA1 区和下托. 其中, DG 区到CA3 区的神经信号传导过程尤为重要, 对癫痫的产生和转迁起着至关重要的作用. 因此, 结合信息科学、控制理论、神经科学、复杂网络理论和解剖学原理, 从动力学角度探究DG-CA3 区关联的颞叶癫痫致病机理将有助于认识神经系统的正常和异常生理功能本质, 为神经电生理实验设计、临床诊疗和手术评估方面提供可靠的理论指导.

在海马体中, 兴奋性信号从DG 区的颗粒细胞产生, 经过苔藓纤维细胞传至CA3 区, 再由锥体神经元中继 (Ahn et al. 2016, Amaral et al. 2007) . CA3 区的锥体神经元对DG 区也有反向投射作用 (Scharfman 2007) . 此外, 一些研究也表明CA3 区锥体神经元不仅对颗粒细胞有兴奋性激发作用, 也通过间接作用抑制颗粒细胞的活动 (Scharfman 2016) . 然而, 在信息传导过程中与兴奋性和抑制性受体相关的反向投射机制还未被揭示.

许多计算神经模型已经被用来研究癫痫的发作机制 (Wendling et al. 2016) . 对于部分癫痫类型, 发作时的脑电信号或局部场电位信号常常会伴有快速振荡放电 (Schiff et al. 2000, Jirsch et al.2006) . 高频振荡放电 (high-frequency oscillations, HFOs) 通常与β频带和γ频带有关 (Neubrandt et al. 2017). Traub 和Bibbig (2000)等人基于锥体神经元轴突间假定的电耦合模型复现了非常快速的振荡放电. 基于对海马CA3 区的解剖学研究, 学者们改进了局灶性癫痫动力学网络模型, 来研究癫痫起始和结束的动力学机制. Van 等 (2005) 建立了一个包含656 个神经元通过弱耦合连接构成的皮质网络模型, 并产生同步性细胞活动与癫痫发作样的簇放电活动. 因此, 神经计算模型的建立对颞叶癫痫的转迁及区域之间连接机制的研究是非常重要的. 如前文所述, 为了更深入地理解颞叶癫痫发作过程中DG-CA3 区的转迁过程和突触连接背后的反向投射机制, 需要建立一个基于神经元特异性的综合性神经网络模型来研究这一过程背后的动力学机制.

因此, 考虑上述未解决问题, 我们基于DG 区和CA3 区解剖学特征与电生理实验表征建立了神经元网络层次的DG-CA3 网络模型. 神经元模型可以将神经元放电的动态过程以数学计算的方式描述出来. Hodgkin 和 Huxley (1952) 提出了Hodgkin-Huxley (HH) 模型, 揭示了神经元离子活动的规律及动作电位的产生机理. 充分考虑神经元特异性, 建模采用HH 类型神经元模拟颗粒细胞、γ氨基丁酸 (γ-aminobutyric acid, GABA) 能中间神经元和O-LM 细胞, 苔藓纤维细胞则基于Pinsky 和Rinzel 提出的两室神经元模型. 构建的两类不同反向投射位置的DG-CA3 网络结构如图1 所示. 忽略门控变量的基本模型动力学方程如下所示 (Pinsky & Rinzel 1994, Yuen & Durand 1991, Wang & Buzsaki 1996, Olufsen et al. 2003, Tort et al. 2008, Ermentrout & Kopell 1998)

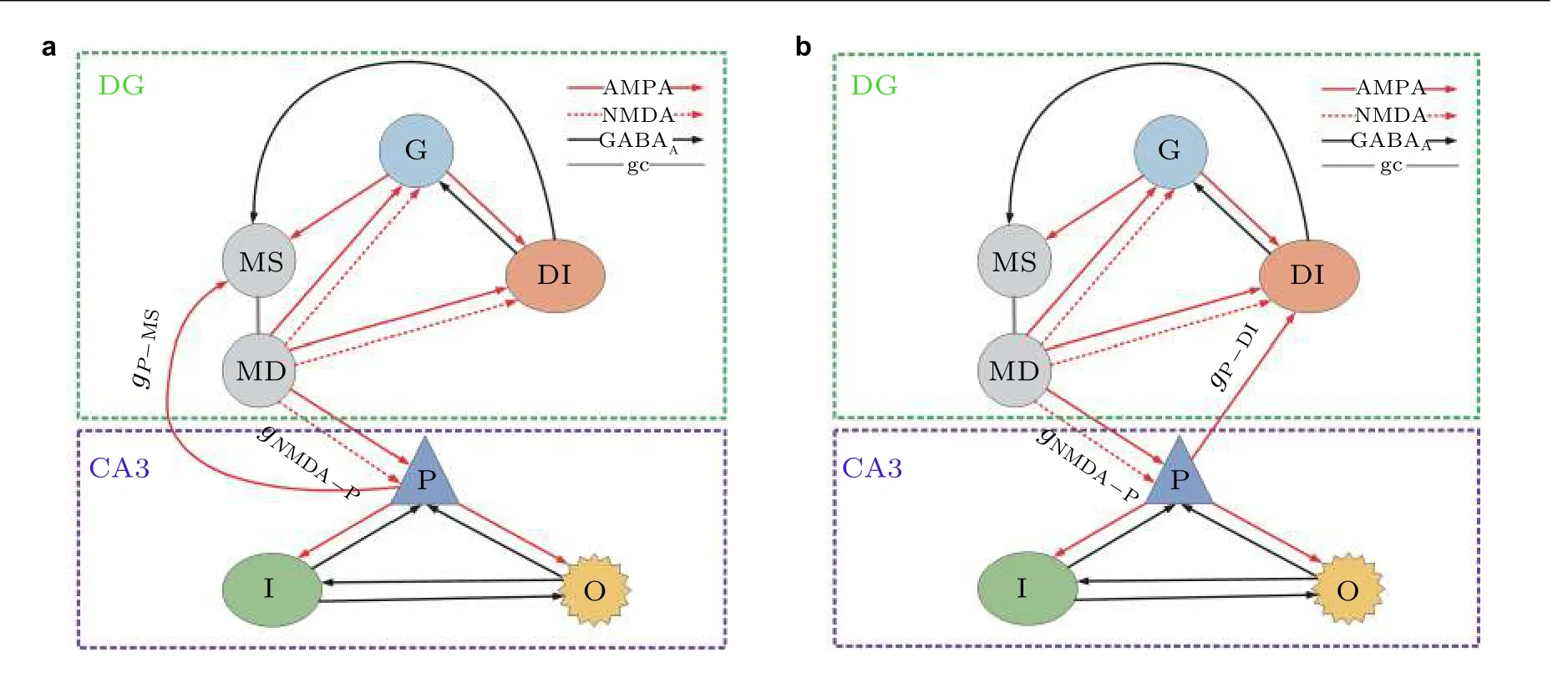
图1 DG-CA3 网络模型连接示意图. (a)反向投射位置从CA3 区锥体神经元到DG 区苔藓纤维细胞的胞体, (b)反向投射位置从CA3 区锥体神经元到DG 区中间神经元 (Zhang et al. 2017)

在模型中, 通过增加突触前神经元谷氨酸递质的释放, 诱发突触后神经元颞叶癫痫样放电的产生. 从图2 可观测到锥体神经元随分岔参数 (苔藓纤维细胞的树突到锥体神经元的突触电导强度) 变化产生丰富的动力学转迁过程. 首先, 当锥体神经元的受抑制程度较低时, 癫痫发作间期呈现缓慢的峰放电. 继续增大分岔参数, 锥体神经元呈现癫痫发作前期的快速峰放电模式. 随后, 锥体神经元进入癫痫发作状态, 并产生节律性簇振荡放电. 最后, 振荡簇分裂为多个小的簇放电, 这也表明了过度的兴奋性电流会对神经元放电产生抑制作用. 由图2 的分析可知, 通过改变谷氨酸型突触电导的连接强度, 锥体神经元可呈现从颞叶癫痫发作间期到发作期的动力学转迁过程.

接着, 对CA3-DG 区的反向投射机理展开研究. 由图3 可知, 增强锥体神经元到苔藓纤维细胞反向连接强度可使DG 和CA3 区神经元细胞产生异常兴奋性活动, 放电主频缓慢上升; 将反向投射位置改变到锥体神经元到DG 区GABA 能中间神经元间, 由于受到间接抑制性反向投射的影响, 两个区域内神经元的放电主频整体情况呈现下降趋势, 神经元兴奋性降低.

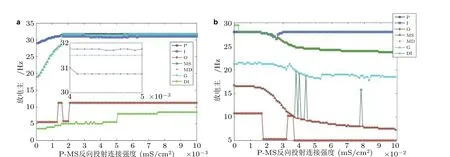
图3 DG-CA3 区神经元放电主频随反向投射强度变化示意图. (a)反向投射位置从P 到MS, (b)反向投射位置从P 到DI (Zhang et al. 2017)

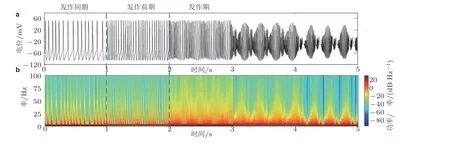
图2(a)锥体神经元的放电时序图, (b)随时间变化的能量谱图(Zhang et al. 2017)

通过结合颞叶癫痫理论与数值仿真模型, 构建了DG-CA3 网络模型来研究颞叶癫痫发作机制, 并基于大脑海马体的连接机制研究了反向投射作用对颞叶癫痫转迁机制的影响. 已有的模型考虑神经元种类较为单一, 缺乏癫痫现象背后深入的连接机制探讨. 本节构建的基于多类神经元的小型网络模型可以描述海马区神经元更丰富的放电节律, 针对颞叶癫痫的解剖学生理结构揭示潜在的神经元动力学机制. 一方面通过详细的定量分析, 发现从锥体神经元到苔藓纤维细胞胞体的谷氨酸型兴奋性反向连接提高了DG 区病态的癫痫样兴奋性, 另一方面, 锥体神经元到DG 区抑制性中间神经元的反向投射作用会阻断DG 区癫痫放电的传播. 构建的网络模型从动力学角度为癫痫疾病的研究提供了新颖的建模方法和研究思路.

2.2 基于改进DG-CA3 海马网络的颞叶癫痫转迁动力学

2.1 节的研究聚焦于DG-CA3 区神经元网络模型, 刻画海马网络内部连接机制对癫痫转迁的影响. 生理实验研究表明, 脑源性神经营养因子 (brain-derived neurotrophic factor, BDNF) 与颞叶癫痫动力学状态转迁过程中受体活化程度的调节有关. 例如, BDNF 增强海马区神经元的兴奋性, 提高神经元放电率进而增加突触后神经元的兴奋性放电 (Shaari et al. 2016) . 更有研究表明,在海马的DG 区, 苔藓纤维细胞中含有大量的BDNF, 兴奋的颗粒细胞通过苔藓纤维将信号传递给CA3 区锥体神经元, 这也表明BDNF 可以增强主神经元的兴奋性 (Scharfman et al. 1999) . 因此, 在改进的DG-CA3 模型中引入了BDNF 调控的兴奋性谷氨酸型天门冬氨酸受体 (n-methyld-aspartic acid, NMDA) 和钙离子调控的α-氨基-3-羟基-5-甲基-4-异恶唑丙酸受体 (α-amino-3-hydroxy-5-methyl-4-isoxazole-propionicacid, AMPA).

另一个研究较广泛的诱发癫痫发作的因子是神经噪声 (Neishabouri & Faisal 2014) . 在宏观的大脑网络模型中, 传入的噪声用来表示远端脑和无法建模的脑组织端的输入 (Jedynak et al.2017) . 基于输入信息的不同, 神经元能产生不同的放电类型. 在神经元中, 传导过程、细胞膜的波动、突触的背景活动和离子通道门的随机开合, 这些都是引起神经噪声的重要因素. Sun 等(2010, 2011) 基于HH 小世界网络研究了离子通道噪声对放电相干性的影响, 指出神经元网络的放电相干性依赖于离子通道噪声源. 此外, 他们还研究了噪声相关性对网络平均放电率的影响,揭示噪声时间的相关性, 诱发癫痫样节律波形的产生. 因此, 在改进的模型中也引入噪声的影响.一方面, 在研究中引入噪声, 是考虑到噪声诱导神经元产生簇放电等生理现象; 另一方面, 系统中的噪声可以诱导系统行为的转迁, 产生如网络同步振荡和同步振荡区域的去同步等动力学行为(Touboul et al. 2011) .

图4 给出了改进型DG-CA3 网络模型的结构示意图.突触前苔藓纤维细胞通过NMDA 受体的活化使钙离子流入到突触后颗粒细胞中. 当谷氨酸型递质从突触前细胞释放到突触间隙, 与突触后活化的NMDA 和AMPA 受体结合, 使突触后神经元兴奋. 成熟的BDNF 与受体TrkB 结合,增加了突触后神经元蛋白质受体NMDA 和AMPA 的活化程度, 因此一个高浓度的BDNF 会激活更多的NMDA 受体, 诱导细胞内钙离子浓度的上升, 增加突触后膜电流. 合成的BDNF 从突触后神经元以活性依赖的方式得以释放. 研究中, 模拟突触间隙的BDNF 为外源性的, 即从外部传入到突触间隙的BDNF, 细胞内部的BDNF 忽略不计. 采用脉冲形式表示BDNF 浓度变化

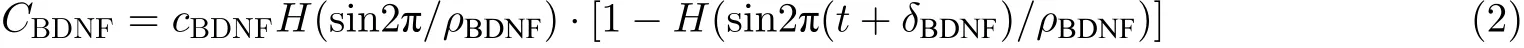
此外, 研究中采用正态分布N～N(Mean,σ2)近似模拟高斯噪声, 表示神经系统的噪声环境.

考虑BDNF 和噪声的联合作用对网络的整体影响. 图5 给出网络整体在BDNF 和噪声联合作用下平均膜电位的变化过程. 从图中可以看出网络对联合作用的响应, 起始呈现下降趋势, 这是由于噪声固定在一个稳定状态, BDNF 发生了变化. 当高浓度BDNF 施加到网络中时, 网络平均膜电位以锯齿状波形振荡, 幅值从-20 mV 到0 mV 范围内增加. 由此可知, 联合作用可使网络的膜电位呈现从低幅值到高幅值放电的转迁, 同时也标志DG-CA3 网络兴奋性的增强.

图6 考察DG-CA3 网络同步性. 当噪声较小时, 网络同步性随BDNF 浓度的增加而得到增强, 随着噪声增加, 同步性指数曲线缓慢上升. 当噪声到达一个较高水平时, 同步性指数曲线呈现一个较复杂的变化趋势, 即随着BDNF 浓度的增大先上升后下降, 这也说明了当噪声过强, 过高浓度的BDNF 会抑制网络的同步性放电. 综上所述, 在一定范围内, BDNF 与神经噪声的综合作用可提高DG-CA3 网络模型的兴奋性, 使平均膜电位从低幅值向高幅值转迁, 进而提升整个DGCA3 网络模型的同步性.

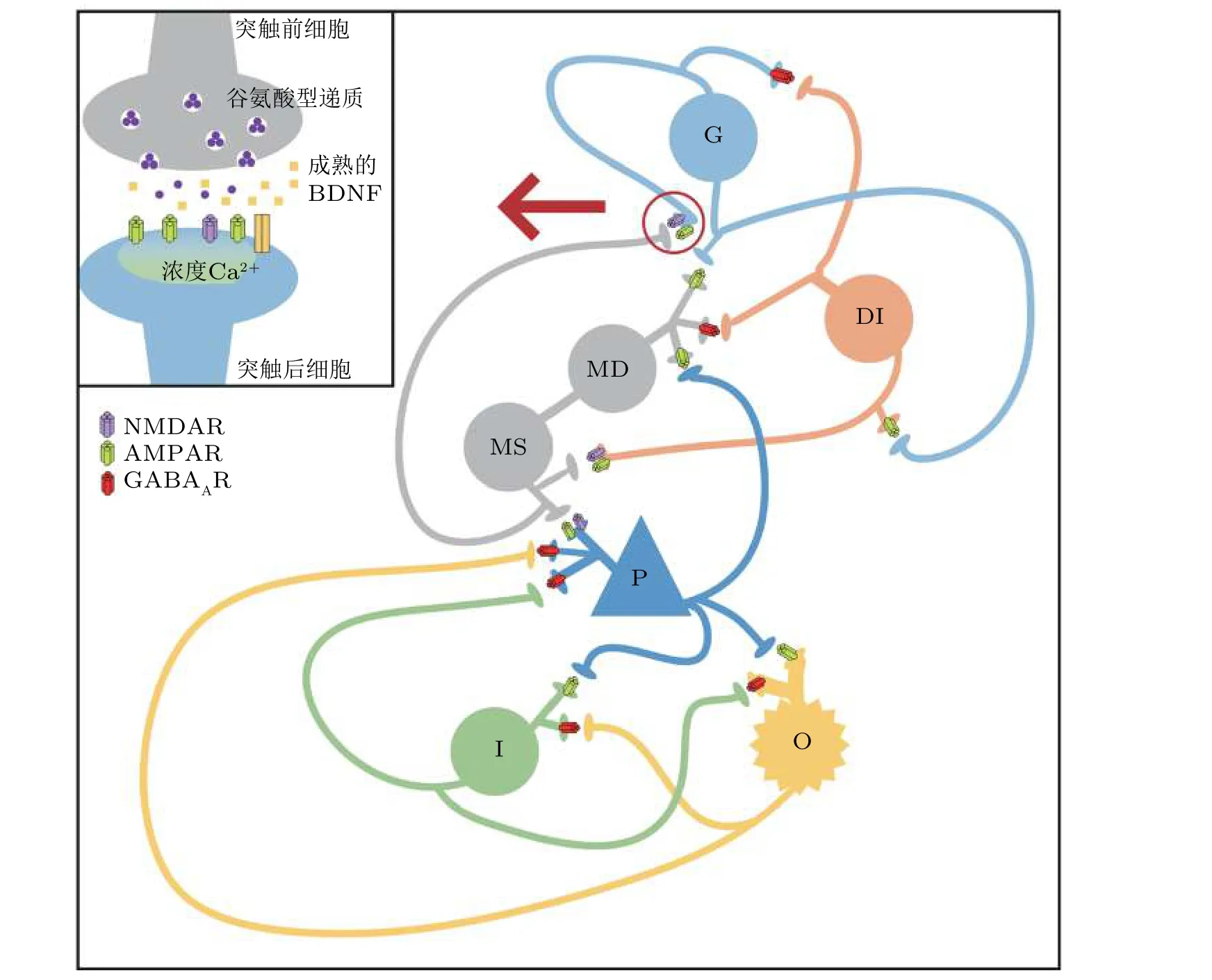
图4改进型DG-CA3 网络模型结构图(Zhang et al. 2018a)

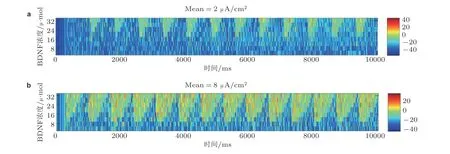
图5网络平均膜电位在BDNF 和神经噪声联合作用下的转迁情况. (a)噪声强度为2 μA/cm2, (b)噪声强度为8 μA/cm2 (Zhang et al. 2018a)

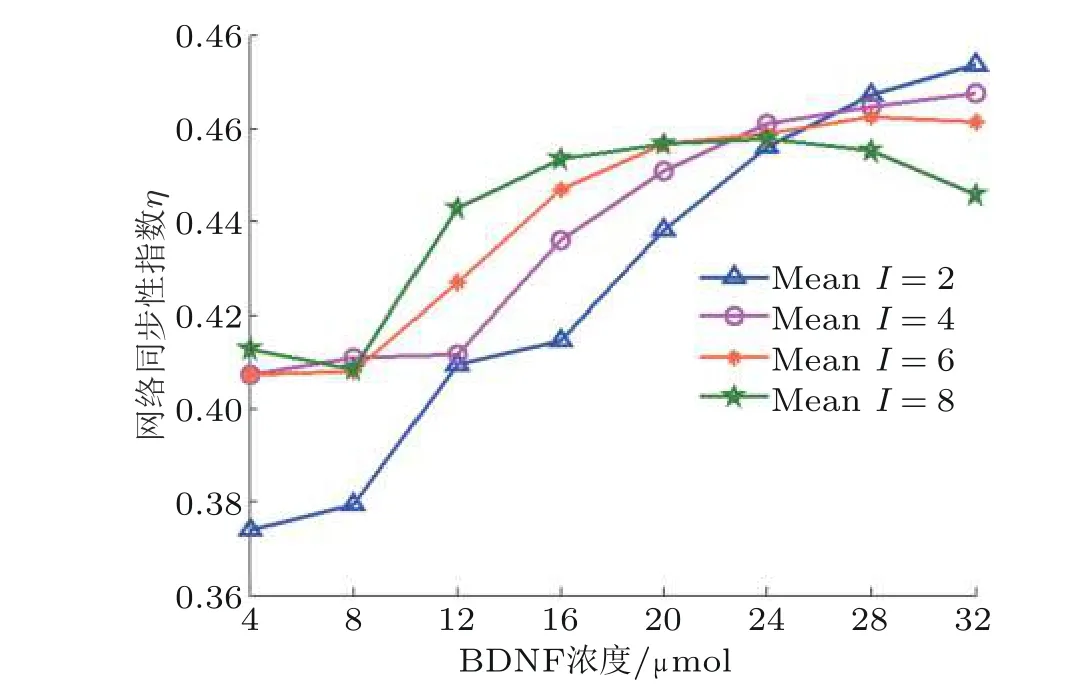
图6在固定噪声强度下, 网络同步性指数随BDNF 浓度变化的演化图(Zhang et al. 2018a)

为了从分子角度进一步研究从正常放电到颞叶癫痫病态同步性放电背后的机制, 从生物数学角度改进了海马DG-CA3 区网络模型. 现有的模型主要基于非线性的基本知识复现癫痫发作现象, 缺乏必要的生物和临床意义. 本节构建的模型可描述针对诱导颞叶癫痫发作的蛋白分子调控癫痫的动力学演化过程. 引入BDNF 和神经噪声, 系统地研究单个神经元和整个网络的动力学特性, 为研究颞叶癫痫动力学机制提供了理论支撑.

2.3 DG-CA3 模体网络的高频振荡动力学建模

研究表明, DG 区和CA3 区之间存在着前馈抑制性 (feedforward inhibitory, FFI) 回路和反馈抑制性 (feedback inhibitory, FBI) 回路 (Neubrandt et al. 2017, Temprana et al. 2014) , 由基本回路组成结构性功能模块, 它们协同工作, 构建高效的癫痫网络, 产生诸如HFOs 等间歇期癫痫样放电. 网络模体的概念最早由Milo 等(2002)提出, 结构模体量化了大脑解剖学的模块构型, 而功能模体表示网络中处理信息的基本单元. 因此, 模体的出现丰富了癫痫网络建模的需要, 对其起到指导作用. 最常见的是3 节点构成的13 种基本模体, 这些小的功能单元根据一定的规律以某种拓扑结构协同配合形成大的功能网络, 完成大脑的认知活动. 关于人脑的结构功能连接机制表明, 在大脑的特殊模体中存在着同步性的放电活动, 特别是在颞叶癫痫的实验数据中已观测到病态同步性的HFOs 活动. 因此, 分别从细胞层次和网络层次对这种病态放电模式的机制进行研究对理解颞叶癫痫的产生是十分重要的. 之前的研究主要集中于单神经元层次上的HFOs 发作机理, 外加电刺激对基于神经元拓扑网络HFOs 产生机理的影响并没有得到很好的解释.

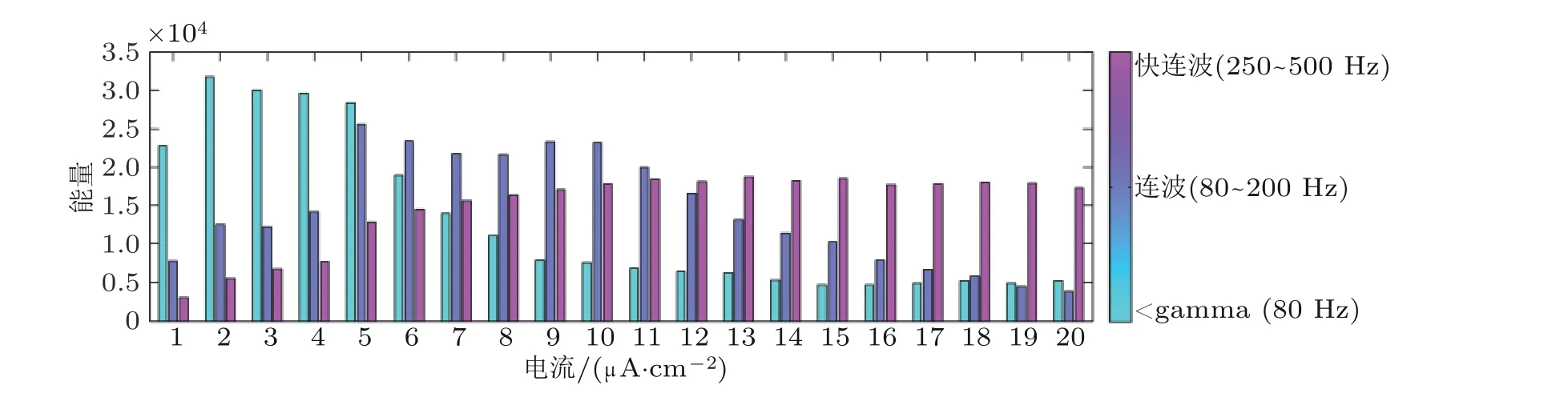
图7节点随外部刺激变化的频带能量直方图(Zhang et al. 2018b)

在过去的几十年中, 关于HFOs 的计算神经元模型得到迅速的发展. Taxidis 等 (2012) 用化学突触连接大鼠中CA3 和CA1 区的两种神经元模型, 这样的连接产生了连波, 并证明化学突触的重要作用. Ratnadurai-Giridharan 等 (2012, 2014)基于CA1 区网络模型研究网络结构在诱发癫痫间期放电过程中的影响. 他们发现GABA 连续的去极化作用是产生HFOs 的关键因素. 随后, Kobayashi 等 (2015) 建立包含颗粒细胞、苔藓细胞、篮状细胞和门中间神经元在内的DG 网络, 模拟发现HFOs 是动作电位的聚类, 并且HFOs 的正向峰值是由于膜电位超慢的去极化过程而产生的.

基于前人对于海马区HFOs 活动的研究, 将独立的DG-CA3 系统视为一个节点, 并考虑外加电流刺激对网络的影响, 外加电流呈现正态分布. 图7 考虑HFOs 频带变化对外界刺激的响应:随着刺激的增加,γ频带能量呈现下降趋势, 而快连波呈现上升趋势, 连波能量的变化则呈现一个钟形曲线, 填补了γ频带和快连波带的空白. 因此, 逐渐增强的外部电刺激能诱导DG-CA3 系统的HFOs 频率产生从γ频带向快连波带的转迁.

在癫痫的产生过程中, 脑区间通过合作可整合单个神经元信号来完成大尺度信息传导的任务. 结构和功能的模体在大尺度网络和单个节点间起到中间尺度模块的作用, 在神经系统的构建过程中扮演着重要的角色 (Worrell et al. 2012) . 因此, 选择3 模体结构刻画DG 和CA3 区的结构特性, 将前面研究的单个DG-CA3 系统封装为一个节点, 这也确保了反向投射位置是在单个系统之内. 基于海马区的连接特性和DG-CA3 系统, 构建了3 节点网络模体结构. 详细的原理结构如图8 所示. 每个节点代表一个DG-CA3 系统, 不同节点之间通过FFI 和FBI 连接,Ki(i=1,2,···,6) 是连接开关.

接着考虑模体中HFOs 在不同刺激条件和抑制性连接作用下的响应特性. 图9 展示了HFOs 关于外部电刺激和抑制性连接变化的综合性统计分析结果. 考虑三种典型的抑制性突触电导连接强度, 即0.0001 mS/cm2, 0.001 mS/cm2和0.01 mS/cm2, 分别计算不同模体结构在不同连接强度与电流影响下的频带能量信息. 研究表明三个频带的转迁是独立于模体结构变化的. 在转迁过程中,γ频带拥有最低的能量平均值, 快连波拥有最高的平均值.

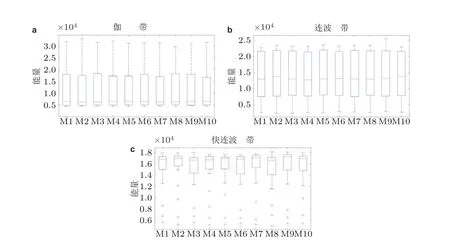
图9 HFOs 对于模体连接结构和外部刺激响应的箱状图. (a)为γ 频带, (b)为连波频带, (c)为快连波频带 (Zhang et al. 2018b)

随后, 探讨基于外部电刺激、抑制性耦合连接和模体结构变化影响下的网络同步性问题. 从图10 可以看出, 当外界刺激从1 μA/cm2增大到5 μA/cm2时, 同步性呈现急剧下降的趋势, 数值保持在0.6 附近. 随后, 继续增大外部刺激, 同步性指数保持不变.对比图10, 增加抑制性连接并不能改变模体间的同步性, 而增加外部刺激可以使模体放电异步, 即达到去同步的效果. 进一步,计算了每个模体在不同情况下的同步性指数总和. 结果可得, 模体M2 的同步性指数总和为38.187 1,即这个结构最易达到模体同步性; 而M8 同步性指数总和最少, 则此结构最不易达到模体同步.

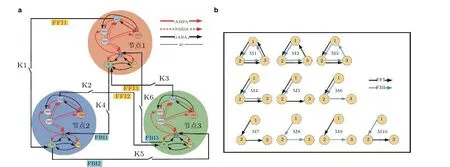
图8(a)基于DG-CA3 系统模体结构的详细原理图, (b)是基于(a)得出10 种可能的连接结构示意图(Zhang et al. 2018b)

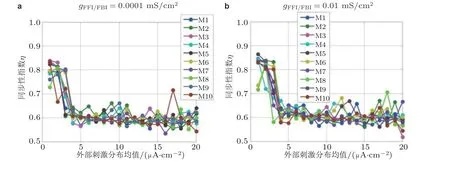
图10同步性指数对不同模体结构、外部刺激和抑制性连接强度变化的响应曲线. FFI 和FBI 抑制性连接电导强度分别为 (a) 0.0001 mS/cm2, (b) 0.01 mS/cm2 (Zhang et al. 2018b)

HFOs 依赖于海马网络结构来平衡海马体对外部刺激和连接性的竞争关系. 已有的模型主要利用复杂网络的基本理论对海马区癫痫神经信息的表达方式进行初步探索, 缺乏针对区域特有结构单元在诱导癫痫产生中的动力学分析. 本节搭建的3-节点网络模体模型可针对产生颞叶癫痫的基本模块分别进行神经元层面和网络节点层面的动力学机制分析. 通过的研究揭示了在抑制性主导的DG-CA3 系统模体中的频率响应特性和同步动力学特性, 为电刺激治疗癫痫提供了可能性的理论验证.

3 癫痫神经场动力学建模分析

神经场模型可以描述与皮层脑电相关的耦合集群的时空转迁. Baier 等 (2012, 2018) 提出了一个具有单一非线性的表征神经元集群活动和场信息的简单神经场振子模型, 它可以呈现癫痫发作中观测到的复合节律的复杂振荡活动. 基于兴奋性神经元集群和抑制性神经元集群活动之间的典型反馈回路, 可以得到如图11 所示的简单神经场振子模型.单个振子模型由一个兴奋性神经元集群 (Ex) 和一个抑制性神经元集群 (In) 组成.每个兴奋性集群都有自突触兴奋性, 同时兴奋性集群与抑制性集群之间相互作用, 即Ex兴 奋In、In反 过来抑制Ex.单个神经场振子模型的动力学方程表示如下

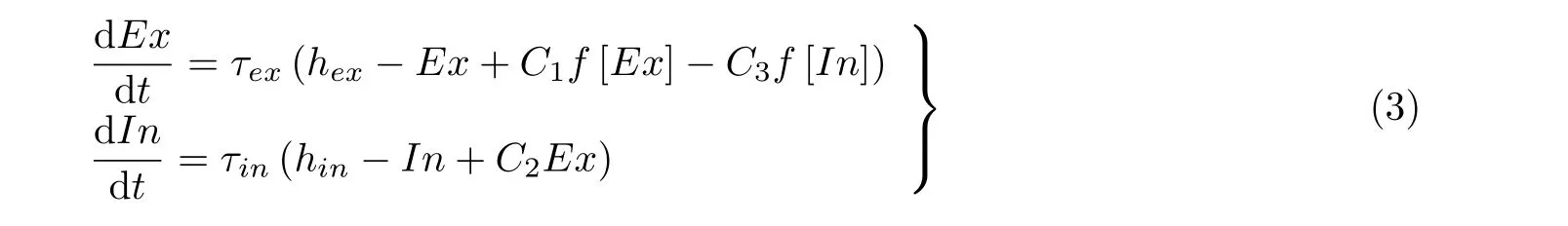
其中,C1,C2,C3是相互连接参数,hex和hin是来自外部源的非特定输入常数,τex和τin是时间尺度常数,f(x)是Sigmoid 激活函数, 其表达式如下

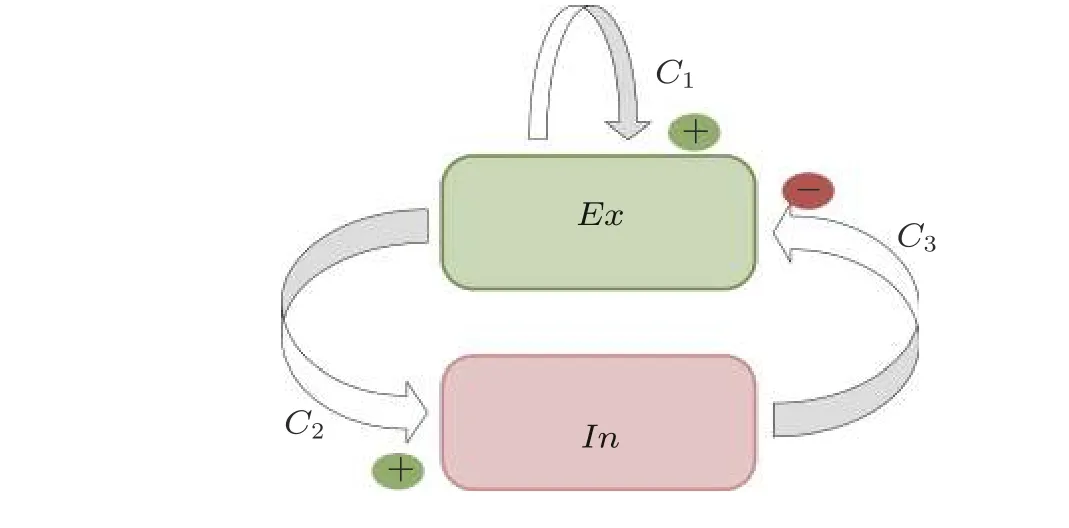
图11单个神经场振子模型, E x表 示兴奋性神经元集群, I n表 示抑制性神经元集群, C 1,C2,C3是两个神经元集群之间的相互作用强度, “+”和“−”分别表示兴奋性和抑制性突触作用

基于简单振子模型, Taylor 等 (2014, 2015) 建立了皮质-丘脑环路神经场网络模型, 来探索丘脑在癫痫发作中的激励机制. 本节分别基于皮层和皮层-丘脑环路的神经场网络动力学模型来展开对癫痫发作动力学机制的研究综述.

3.1 皮质局灶癫痫的牵制控制动力学建模

3.1.1 慢变量驱动的双耦合振子模型的动力学分析

局灶性癫痫样簇放电现象是由慢动力学产生的 (Izhikevich 2007) . 在介观层面, Jirsa 等(2014)提出一种癫痫发作的动力学模型来评估慢变量的影响. 在平均场层次, Liley 和 Matthew(2013) 通过增加慢变量建模, 产生簇放电活动, 他们猜测这个附加的慢变量可能代表皮质内、皮质间和皮质下的叠加效应. 具体地, 他们猜测这个慢变量系统可能起源于丘脑-皮质的反馈、长时程皮质-皮质纤维系统的传导特性, 或者是由于突触活动产生的慢变化, 如胶质细胞的摄取 (损耗) 和重摄取 (恢复) 过程. 基于有关星型细胞 (胶质细胞的一种) 的猜测 (Lalo et al. 2014, Buskila et al. 2019) , 考虑一个由双耦合振子和一个慢变量组成的简单系统, 这个系统可以呈现在继发性癫痫发作中观测到的局灶性癫痫复合节律振荡活动 (Zhang et al. 2020b) . 每个振子由一个兴奋性集群和一个抑制性集群组成, 每个兴奋性集群都有自兴奋性, 振子间拥有相似或者不同的时间尺度. 振子间的耦合是双向的但具有不同的耦合连接强度, 这里考虑耦合强度作为分岔参数. 每个振子都与慢变量相连, 双耦合振子的连接结构如图12(a) 所示. 在式 (3) 和 式(4) 的基础上增加下列微分方程, 以描述慢变量驱动的双耦合振子的时间演化 (Baier et al. 2018)

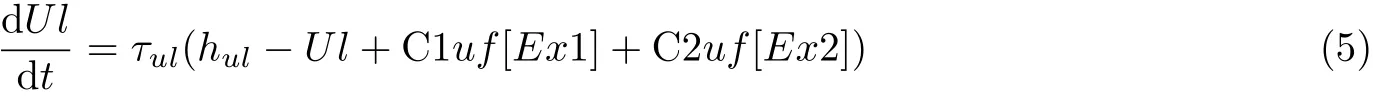
其中Ex1 和Ex2 为兴奋性神经集群,In1 和In2 为抑制性神经集群,Ul为慢变量,f是Sigmoid 函数,C1u和C2u变 量是连接强度,hul变 量为外部输入,τul变量为时间尺度常数.

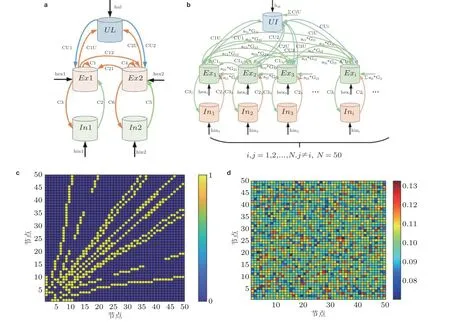
图12(a)慢变量调控的双耦合振子结构示意图(Zhang L Y et al. 2020b) , (b)由全局慢变量调控的无标度局灶性致痫网络结构示意图, (c)为网络连接矩阵, (d)为耦合强度矩阵图(Zhang et al. 2020a)

主要考虑不同参数作用在相同时间尺度或不同时间尺度的双耦合振子, 特别是分析它们在慢变量驱动下的动力学转迁行为与局灶性癫痫的发作机制. 图13 表明高幅值慢发作的振荡波形从一个簇放电到另一个簇放电间是显著变化的, 这说明全局吸引动力学是准周期或弱混沌的. 振荡状态起始于两三个频率增加的峰放电, 这也对应着不变环上的鞍结分岔; 剧烈活动时振子的时间序列在振荡区域内先表现为一个较慢的活动, 随后频率增大. 幅值开始时较为规则, 随着系统动力学向不稳定状态过度, 幅值也变得慢而高; 小幅值快发作则对应于沿两个稳定状态变化的双稳态过程, 伴随超临界霍普夫分岔.

3.1.2 局灶性癫痫致痫网络的动力学转迁

致痫灶网络的动力学特性包括在不同显著状态之间转迁的能力, 如何识别驱动致痫网络从静息态到癫痫态的关键动力学特征是其中的一个重点研究问题. 脑网络是一个具有高度自治特性的复杂非线性动力学系统 (Lopes da Silva et al. 2003a, 2003b) , 特别是癫痫网络中含有一些自治参数, 这些参数的改变会影响全局动力系统的结构. 当这些自治参数变化出现潜在的低维吸引子分岔时, 癫痫就会发作. 在神经系统中, 脑活动具有无标度特性 (He et al. 2010) . 癫痫是一个动力学现象也服从无标度行为特性. 基于精准的记录技术与网络拓扑理论, 研究者提出一种度服从幂律分布的无标度网络 (Barabási & Albert 1999) . 特别是, 在无标度癫痫网络中, 异常振荡是由无标度网络的中心兴奋性细胞引起的 (Morgan & Soltesz 2008) , 并且这些细胞在癫痫的传播过程中起到枢纽的作用 (Picardo et al. 2011, Cossart 2014) .

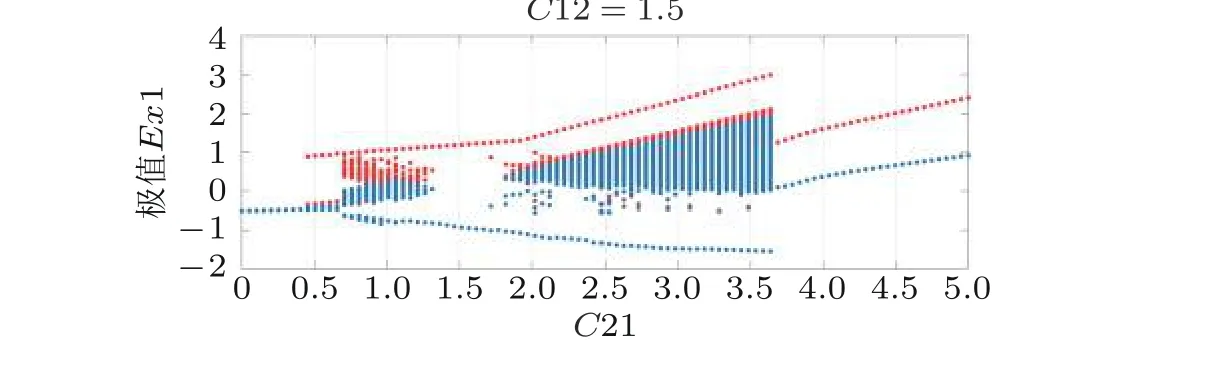
图13具有相同时间尺度的耦合振子模型模拟癫痫发作状态 (红色局部极大值, 蓝色局部极小值) 关于耦合参数演化的转迁动力学 (Zhang et al. 2020b)

对应无标度的局灶性致痫网络模型, 每个节点为单个振子模型, 包含一个兴奋性和一个抑制性集群. 无标度网络是一个自治网络, 节点的度服从幂律分布. 概率P(k)代表网络中的一个节点与其他k个节点相连的概率衰减服从幂律分布, 且这个概率服从泊松分布P(k)=[λk·exp(-λ)]/k!,无标度网络的概率在0 ～ 1 之间. 具体的网络连接规则如下: 网络起始于少数节点, 然后每次增加具有m条边的新节点. 为了确定优先连接性, 假设概率满足情形为一个已知节点i与一个新节点连接取决于新节点的连接性ki. 依据这个规则, 网络会拓展为一个拥有t+m0个节点,mt条边的随机网络, 其中t代表更新的步长 (Albert & Barabási 2002) . 随着网络的增长, 网络将会自行整合, 形成一个无标度的稳定结构.

基于慢变量驱动的双振子耦合模型, 可以考虑一个拥有50 个振子的无标度网络, 网络中一个节点代表一个振子, 即拥有一个兴奋性集群和一个抑制性集群. 无标度网络的连接矩阵为A=(aij)N×N.为了获得更真实的连接性, 采用高斯分布的耦合强度矩阵G=(Gij)N×N, 进而改变高斯耦合强度矩阵为G=CG, 其中C为高斯分布的平均幅值. 图12(b)给出整个网络连接结构示意图, 图12(c)为网络连通性, 图12(d)为耦合强度矩阵的分布情况, 并应用慢变量作为生物标记, 可以判断局灶性癫痫的不同阶段. 通过定义与癫痫振荡相关的超兴奋性, 提取致痫网络病态时间域特征. 这里采用相位锁相值 (phase locking value, PLV) 提取每个信号的瞬时相位特征,PLV的计算公式如下

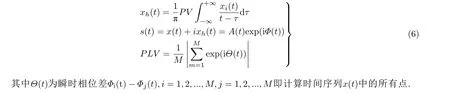
基于之前对局灶性癫痫动力学转迁的研究 (Iasemidis et al. 2009) , 可以考虑在相似时间尺度下关键参数变化对无标度耦合神经网络动力学行为转迁的影响. 从图14 可知, 通过改变网络关键参数, 无标度致痫神经网络模型可以复现从静息态到间歇性发作态, 到持续性发作态, 再到饱和放电态的转迁过程.

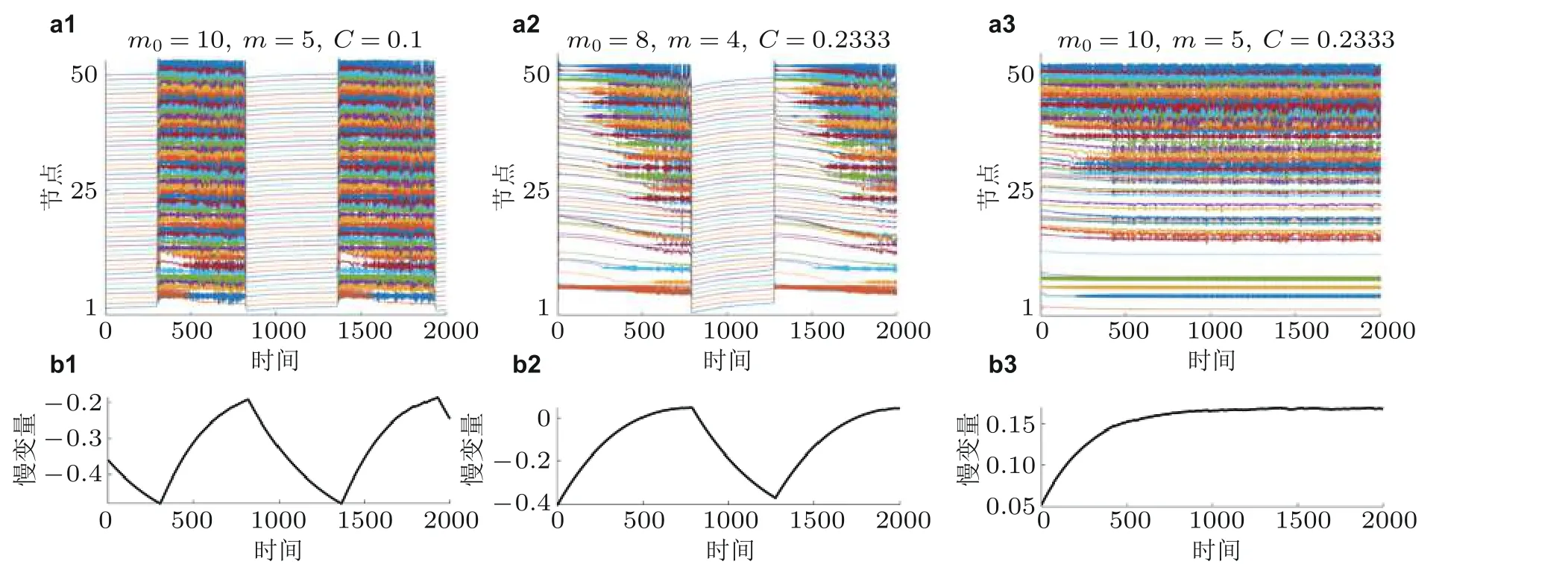
图14网络振子 (上) 和慢变量 (下) 的时间序列图. (a1)和(b1)为间歇性癫痫的慢速高幅值发作状态,(a2)和(b2)为间歇性癫痫的快速低幅值发作状态, (a3)和(b3)为持续性癫痫发作状态 (Zhang et al. 2020a)

接着, 需要刻画网络结构参数和平均耦合强度对网络动力学转迁的影响. 应用慢变量波动大小和数值范围作为划分的生物标记, 自动地区分网络的不同状态. 在图15 中, 网络的不同状态分别为静息态 (QS) 、间歇性发作状态 (ISS) 、持续性癫痫状态 (SES) 和饱和放电状态 (SDS) . 深蓝色代表的QS 出现在m= 1 且C较小时. 当m0增大到10 时, QS 状态消失. 当m0较小时, 蔚蓝色代表的SES 成为系统的主要状态. 当m0增大时, 相继出现ISS (绿色区域) 以及SDS (黄色区域) . 当m0继续增大, ISS 活动受到抑制. 然而在确定的C值内, 在大多数结构中可以达到ISS. 对于SDS, 它起初出现在右下角区域, 这个区域拥有较强的C和较大m值. 当m0增大时, SDS 占领了大部分的参数与状态空间区域, 并成为系统的主要状态.基于上述的解释, 可以理解耦合强度是如何依赖网络结构多样性与小规模连通性, 进而影响了网络动力学转迁行为.

除了一般性的动力学特征, 需要定量地考虑局部或者全局的动力学特征与网络结构因素的依赖性. 依据图15 的参数-状态空间图, 模拟多组间歇性发作状态活动, 量化癫痫样振荡时间序列的PLV, 视慢变量为生物标记, 自动删除静息态, 把放电部分重组为新信号, 这样可以忽略静息部分的干扰, 得到叠加后的有用的信号. 从图16 中可以明显看出, 较强的全局耦合强度可使致痫网络达到较高的相位同步状态. 相似地,PLV与节点平均度具有鲁棒的相关性. 通过上述动力学特征的分析, 可以依据网络结构和全局耦合强度区分局灶性癫痫不同的状态, 并且更深入地理解网络内部相位同步的关系, 这些分析为基于致痫网络动力学特征的控制策略奠定了理论基础.

3.1.3 牵制控制的癫痫调控策略

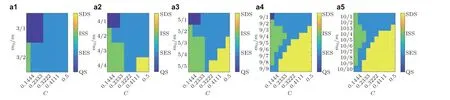
图15局灶性癫痫致痫网络的状态转迁空间. 横坐标为平均耦合强度, 纵坐标为网络结构参数的比例,不同的颜色代表不同的状态. 从(a1)到(a5), 初始节点的个数分别为3,4,5,9 和10. 横坐标为耦合强度C, 纵坐标为网络结构系数的比例m0/m (Zhang et al. 2020a)

研究者针对复杂网络, 如无标度网络的一致性和同步性问题提出了牵制控制理论. 基本的牵制控制理论可描述为, 控制器只用牵制那些连接度高的节点, 对它们施加以牵制误差向量为函数的控制信号 (Fan & Chen 2005, Zou & Chen 2009) . 研究表明, 基于中心节点区域的控制网络交互可能会对调节多样的目标导向功能的脑网络研究十分重要 (Rosch et al. 2017) . 然而, 脑区中的连接度是很难被直接测量出来的. 通过引入牵制控制理论, 设计控制策略刺激一小部分具有高PLV值的节点, 而这些节点对应着强连接性.

在刺激策略中使用固定刺激强度的直流经颅电刺激 (transcranial direct current stimulation,tDCS) 作为刺激模式, 刺激施加在兴奋性神经集群上. 图17 中给出了刺激实例来检验刺激不同数量的节点产生的有效性: 在没有刺激的情况下, 致痫网络呈现重复性的癫痫簇放电活动; 刺激一定比例, 整个网络对刺激产生一个响应, 随着刺激的进行, 间歇性发作状态受到瞬间抑制, 而后恢复到间歇性发作状态; 提升控制比例, 间歇性发作活动迅速受到抑制, 在刺激时间内没有再反复出现间歇性发作状态.

而后, 考虑网络结构、刺激节点百分比和tDCS 刺激强度之间的关系. 从图18 可以得出, 当初始节点较小时, 网络需要较弱的刺激实现从间歇性发作到静息态的转迁, 且相同m0中m值越大需要的刺激越小. 因此, 定量研究描述局灶性致痫网络结构和刺激节点比例之间的关系, 这为基于实际数据设计最小刺激能量的控制策略提供了理论依据.

3.2 失神癫痫的皮质−丘脑环路网络动力学建模分析与调控

前一节给出了局灶性癫痫发作传播及其控制的动力学建模方法和仿真结果.但是很多全面性癫痫如失神癫痫 (Berman et al. 2010, Engel et al. 2008) 和强直-阵挛性癫痫发作 (Gao et al. 2015,Dobesberger et al. 2015) 被证实是由于皮质和丘脑环路 (thalamocortical circuit, TC) 的信息交换异常所致.电生理学实验已经揭示大脑皮层中癫痫失神发作和强直-阵挛性发作之间可以双向转迁 (Mayville et al. 2000, Shih & Hirsch 2003) , 其中失神癫痫患者发作时, 临床脑电图 (EEG) 中可以观察到典型的2 ～ 4 Hz (约3 Hz) 的 (多) 棘慢波放电 (spike and wave discharges, SWD). 但是皮质网络与丘脑之间相互连接构成复杂的网络, 确定出丘脑对皮质癫痫的作用机理, 特别是表征癫痫样病态节律活动及其转迁的关键生理参数还需要进一步的理论验证. 因此, 接下来将分别给出丘脑中继核和丘脑网状核对癫痫失神发作作用的动力学机制分析.

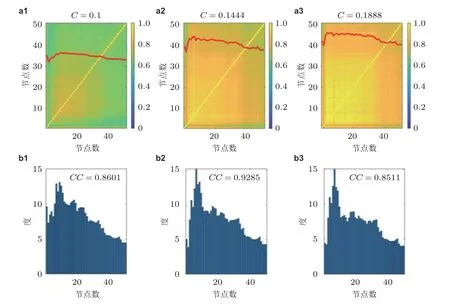
图16平均PLV 值的矩阵热图(a), 耦合强度分别为0.1, 0.144 4 和0.188 8, 与对应的平均网络度分布直方图(b), CC 为节点PLV 与度的相关系数 (Zhang et al. 2020a)

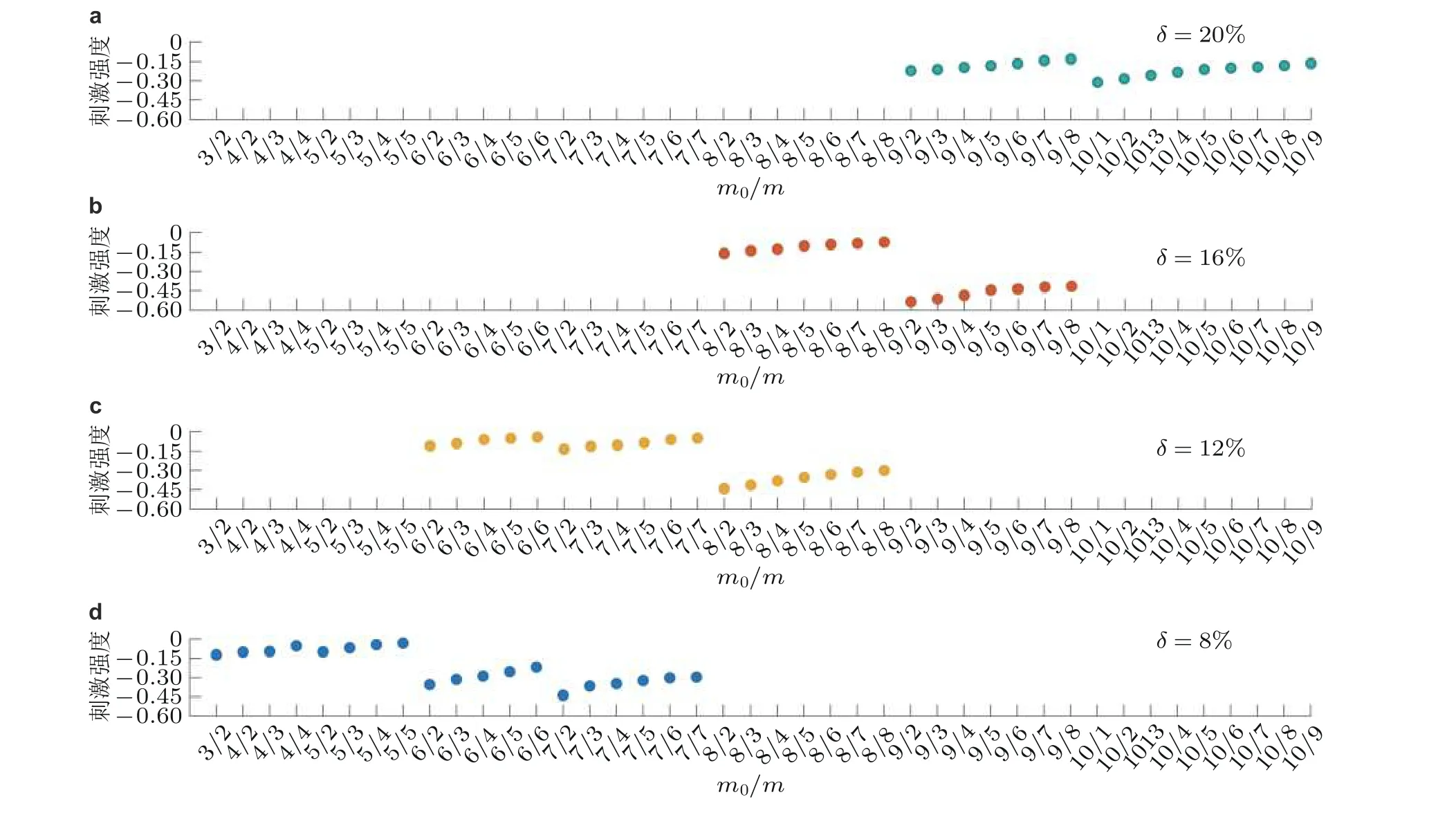
图18基于多样网络结构的牵制刺激策略效果图. (a) ～ (d)分别为刺激20%, 16%, 12%和8%的节点(Zhang et al. 2020a)

3.2.1 丘脑中继核对癫痫失神发作的动力学作用机制

众所周知, 丘脑的中继神经元具有接受并中继皮质信息的能力, 对皮质网络信息流的正常表达起着至关重要的作用. 由图19(b)所示, 丘脑中继核TC 与皮层兴奋性神经元PY 之间构成了典型的递归兴奋性回路; 同时TC 与抑制性中间神经元IN 和兴奋性PY 构成了前馈抑制性回路.这里, 主要基于这两种回路机制来理论验证电生理实验发现的皮质与丘脑环路信息交换异常导致的癫痫失神发作.

皮质-丘脑回路的神经场模型可抽象描述如下 (Rodrigues et al. 2007, 2009)

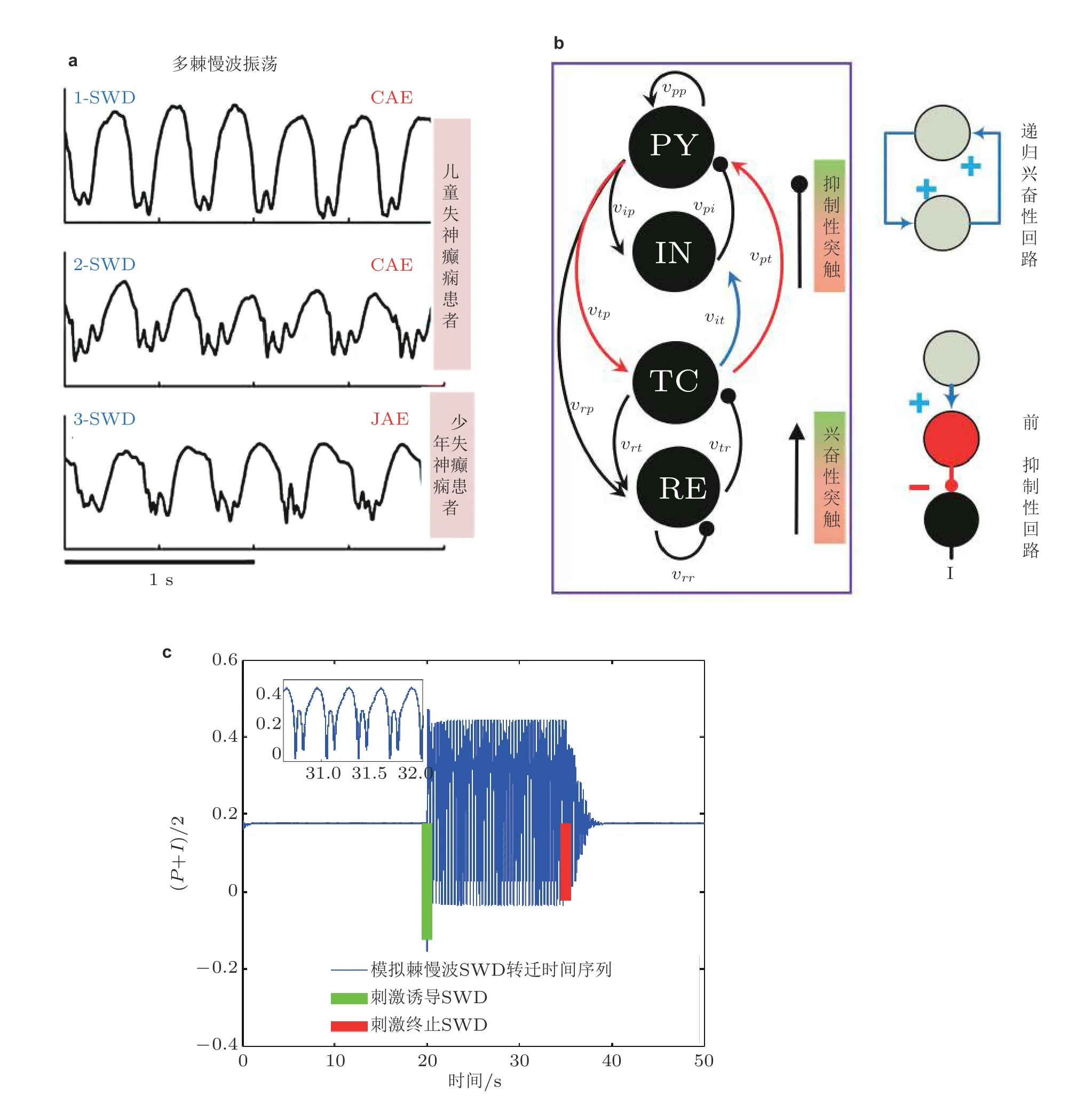
图19(a)来自三名不同癫痫患者发作的脑电图记录 (Marten et al. 2009) , 上图和中图为儿童失神癫痫患者 (CAE) 脑电图, 下图为青少年失神癫痫患者 (JAE) 脑电图. (b)皮质−丘脑网络框架: 皮质子系统由兴奋性 (PY) 锥体神经元集群和抑制性 (IN) 中间神经元集群组成; 丘脑子系统由丘脑网状核 (RE) 和中继核 (TC) 组成 (Fan & Duan 2017) . 皮层-丘脑环路 (PY-TC) 形成的递归兴奋性微回路和 (TC-IN-PY) 形成的前馈抑制性微回路 (Paz et al. 2015). (c)皮质−丘脑环路中皮质子网络神经元集群PY (P) 和IN (I) 平均动力学 ( (P+I) /2) 时间序列图: 单脉冲刺激 (绿竖直线) 诱导的SWD 振荡和单脉冲刺激 (红竖直线) 诱导的SWD 振荡终止 (Fan & Liu 2016)

临床电生理实验显示, 癫痫失神发作过程中棘慢波SWD 放电状态与背景的低幅高频振荡状态交替出现. 如图19(c)所示, 通过皮质-丘脑神经场理论模型也模拟了单脉冲刺激扰动下癫痫的SWD 放电状态与背景状态之间的双向转迁行为. 因此皮质-丘脑模型已成为研究癫痫发作机理的常用模型. 基于皮质-丘脑环路系统重点考虑了由丘脑中继核与皮质组成的递归兴奋性回路对癫痫发作的影响, 依此来理论验证电生理实验假设即皮质和皮下丘脑的信息交流异常可诱发癫痫发作行为. 研究发现, 当皮质和丘脑之间的相互作用呈现近似负相关时 (见图20) , 即丘脑能够过多地接受而不能有效地中继皮质的信息, 或者是过少地接受却异常反馈皮质信息时, 就会导致皮质网络出现癫痫失神发作的典型2 ～ 4 Hz 的棘慢波SWD 振荡. 另外, 理论研究表明在皮质和丘脑相互作用的双参数区域存在由稳定的焦点和稳定的极限环组成的双稳定性区域 (见图21, 即在生理上对应皮质的低饱和放电和癫痫失神发作的棘慢波SWD 振荡) , 在此区域, 电刺激干扰可以重复诱发和消除癫痫的棘慢波振荡, 这为癫痫的间歇性发作和临床闭环控制治疗手段提供了一定的理论依据.

另外, 如图20 所示, 皮质-丘脑之间信息交互异常也会诱导癫痫失神发作与其他如强直-阵挛性发作和饱和状态之间的双向转迁. 详细研究发现 (图21) , 这些相互转迁行为是由系统关于皮质-丘脑相互作用参数经历的一系列如超 (亚) 临界霍普夫分岔 (HB) 和极限环分岔 (LPC) 形成的. 分岔也会诱导出不同的稳定和不稳定平衡点吸引子与极限环吸引子, 从而当系统位于多稳定态参数区域时, 刺激扰动可能会使得不同发作状态的终止或相互转迁. 从动力系统的角度来讲, 微分方程状态空间的双稳态区域存在一个分界流形, 即分界超平面, 适当的刺激可以驱动系统的动力学状态从一种稳定状态穿越分界超平面转迁到另一种稳定态. 另一方面, 电生理实验中特定的电刺激可以终止癫痫的发作, 同时也观察到了刺激实验失败的例子. 这可能是因为当系统动力学处于单稳态的病态情形时, 无论如何调节刺激参数也不能有效改变系统的病态动力学定性行为, 导致通过电刺激干扰来预防和控制癫痫的失败结果.

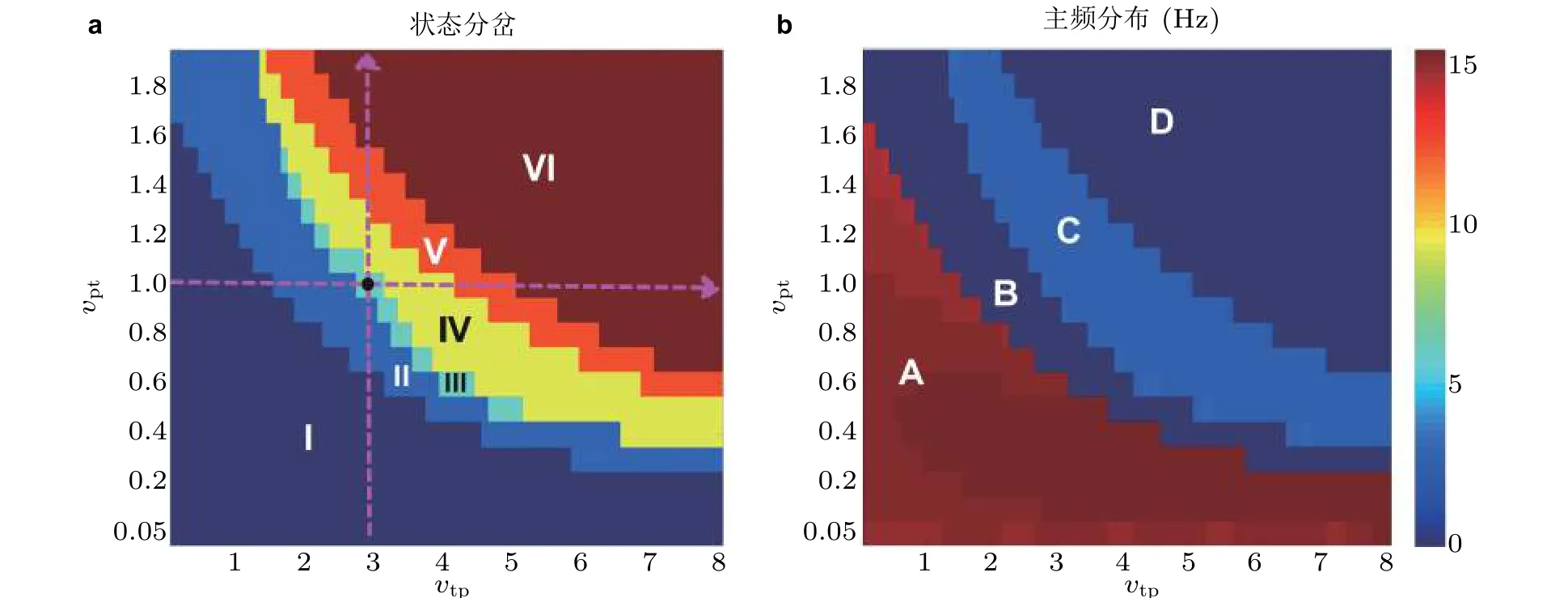
图20

研究发现, 丘脑中继核前馈抑制作用对皮质的功能活动比前馈兴奋作用具有更显著的影响,而前馈抑制在理论研究中往往被忽略. 鉴于此, 在皮质-丘脑环路中引入前馈抑制性连接, 提出了改进的计算模型, 由此系统地研究了前馈抑制和前馈兴奋作用对癫痫发作转迁的综合效果. 首先改进系统可以模拟电生理观察到的癫痫的周期2/3/4-SWD 棘慢波振荡 (如图19(a)) , 反向棘慢波和阵挛性振荡以及饱和放电模式等丰富的动力学转迁行为, 且通过快慢动力学分析给予了动力学解释. 特别地, 由前馈抑制和前馈兴奋组成的2D 参数平面上, 可以确定癫痫失神发作与强直阵挛性发作之间的相互转迁路径. 观察发现在弱前馈抑制性调节下, 前馈兴奋性作用可以诱导系统从癫痫强直振荡到失神发作的转迁, 而前馈抑制性作用的增强又进一步可以诱导癫痫失神发作向阵挛性发作的转迁 (见图22) . 研究结果为前馈机制参与癫痫发作的病理机理提供了理论支持.

3.2.2 丘脑网状核对癫痫失神发作的起搏器作用

研究证实, 癫痫和睡眠共享皮质-丘脑回路机制 (Sitnikova 2010, Siapas & Wilson 1998) . 特别地, 已有电生理实验假设认为癫痫的棘慢波是睡眠纺锤波的转化形式 (Lopes da Silva et al. 2003a,2003b; Shouse et al. 2000) . 图23 展示了电生理实验和临床观察到的癫痫失神发作SWD 与睡眠丘脑中继核与皮质组成的递归兴奋性回路作用下皮质网络中集群平均动力学关于参数状态变化分岔分析. (a) 状态分岔图, 包括失神癫痫SWD 振荡 (III,IV) , 强直 (tonic) (I) 和阵挛性 (clonic)振荡 (V) , 以及低/高 (II/VI) 饱和放电 (saturated firing) 等; (b) 对应状态的主频演化, A/C 对应高/低频振荡, B 和D 对应背景正常状态 (Fan & Liu 2016)纺锤波之间的周期性转迁行为. 但还缺乏相应的理论证据. 至今还未有一个统一的理论模型来同时描述癫痫波与睡眠波, 以及它们之间相互演化的动力学行为. 根据电生理实验EEG 观察结果,剖析癫痫与睡眠之间的本质联系, 建立符合生理意义的癫痫失神发作棘慢波SWD 放电与睡眠纺锤波相互演化的时空扩展的皮质-丘脑回路网络动力学模型, 研究癫痫波与睡眠波之间产生、传播和演化的时空动力学复杂行为, 揭示它们的动力学机理, 为临床干预和控制癫痫与改善睡眠提供一定的理论指导.

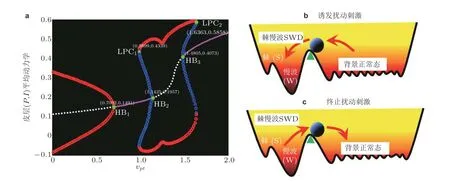
图21(a)皮质平均动力学分岔分析 (对应图20 竖直线虚线箭头) , 其中粉色/白线代表稳定/不稳定的平衡点, 红/蓝线代表稳定/不稳定的极限环. 系统依次经历超临界和亚临界霍普夫分岔 (HB) 以及极限环分岔 (LPC) . 双稳定吸引子及其吸引域示意图: (b) SWD 诱导刺激扰动, (c) SWD 终止刺激扰动. 扰动使得系统 (小球) 从一个稳定状态越过临界状态 (三角形) 转迁到另外一个稳定状态 (Fan & Liu 2016)

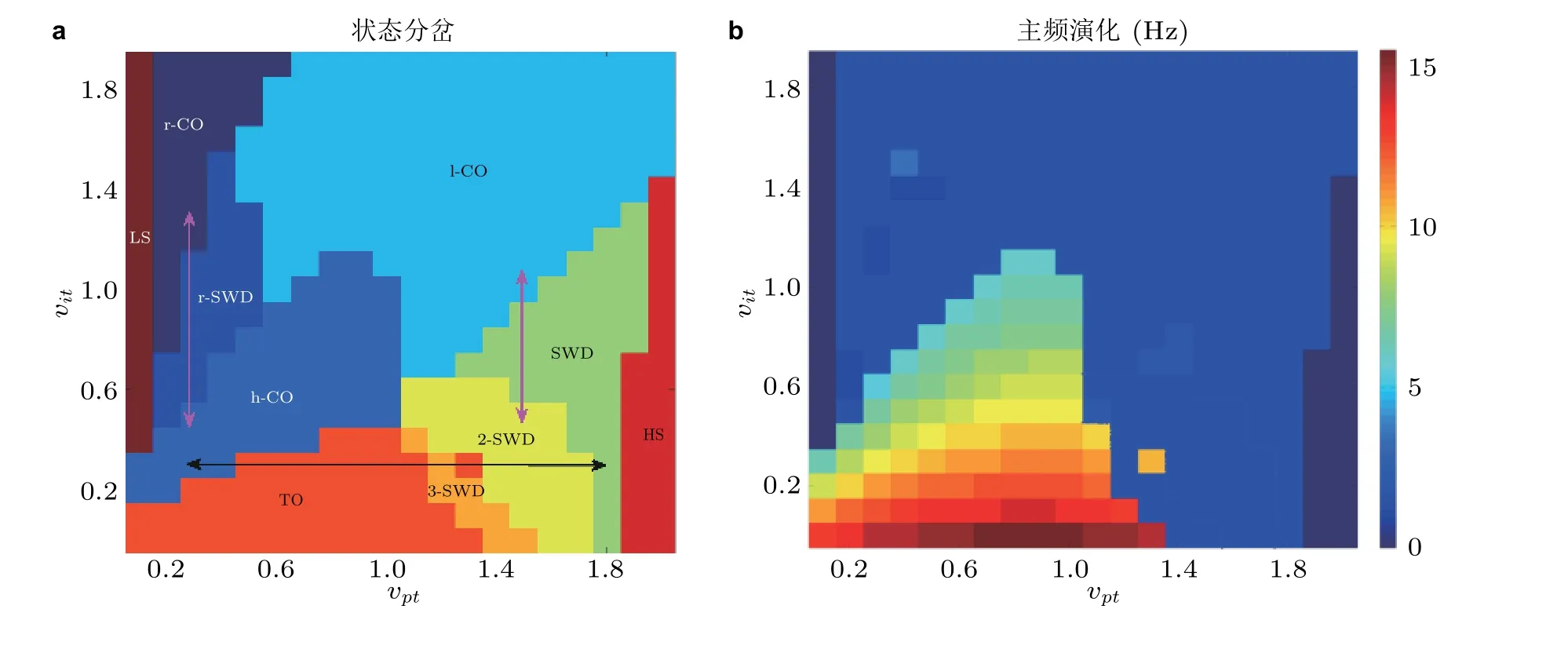
图22由前馈抑制和前馈兴奋组成的2D 参数平面上可以确定癫痫失神发作与强直阵挛性发作之间的相互转迁路径. (a)状态演化, 包括高饱和 (HS) 和低饱和 (LS) 放电, (多) 棘慢波SWD, 2-SWD 和3-SWD 振荡, 反向棘慢波 (r-SWD) , 强直 (TO) 和低/高频阵挛性 (l/h-CO) 以及反向阵挛性 (r-CO) 振荡等; (b)对应的主频演化 (Fan & Duan 2017)

丘脑网状核 (RE) 在调控神经网络信息处理平衡中是极其关键的, RE 可以协调大脑不同区域的慢波振荡. 实验结果已经表明丘脑网状核在睡眠或癫痫发作过程中起着控制纺锤波和棘慢波放电 (SWDs) 的起搏器作用 (Lee et al. 2013; Steriade et al. 1985, 1987; von Krosigk et al. 1993) ,即丘脑网状核可以调节癫痫性SWD 和睡眠纺锤波的发作和传播. 基于发展的空间扩展的皮质-丘脑环路网络动力学模型, 如图24(a) ～ 图24(c)所示, 单脉冲刺激丘脑网状核可以诱发电生理实验和临床观察到的癫痫的失神发作以及与睡眠纺锤波的周期性转迁, 同时刺激产生的SWD 可以通过网络环路下行投射路径在整个网络不同节点进行传播, 从而理论证实了丘脑网状核对失神癫痫波向睡眠纺锤波转迁的起搏器作用. 特别地, 由SWD、纺锤波 (spindle) 和正常背景状态(即平衡态或低幅阈下周期振荡, 对应稳定极限环) 组成的三吸引子共存机制, 构成了这些状态时空演化的动力学基础 (见图24 (d) , 图24 (e) ) , 为癫痫发生发展机制提供新的理论见解.

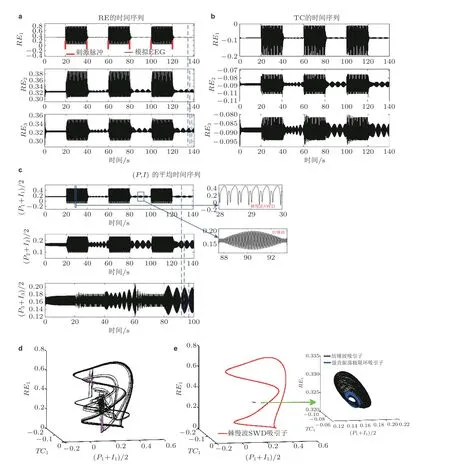
图24(a) (b) (c)环式连接的3 室耦合模型网络, 周期单脉冲刺激 (红色竖直线) 从 t=20 s开始间隔20 s依次施加刺激在第一室的RE, 三室的不同核团都呈现SWD 与纺锤波振荡的周期性转迁(c)右侧为局部放大图. (d) (e)纺锤波吸引子 (spindle, 黑色) , 极限环吸引子 (低幅度强直振荡, 背景正常状态, 蓝色) 和SWD 吸引子 (红色) 共存状态. 粉色箭头代表对RE 施加的刺激. (e)右侧的局部放大图(Fan et al. 2017b)

3.3 皮质−丘脑环路时滞对癫痫失神发作的动力学机理

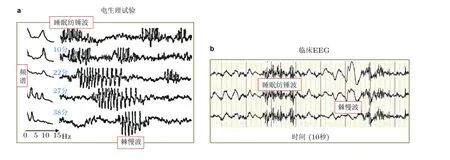
图23(a)实验观察到的睡眠纺锤波(spindle)向癫痫棘慢波 (SWD) 转迁 (Kostopoulos 1981, Kostopoulos et al. 2000), (b)癫痫患者睡眠期间颞叶电极的脑电图记录显示10 s 的睡眠纺锤波和棘慢波振荡 (Fan et al. 2017c)

神经信息传递时滞是神经系统的固有特性, 它能改变系统的动态行为并增加系统复杂性. 在癫痫的皮质-丘脑网络中已经分别单独考虑过丘脑子系统内的时滞 (Chen et al. 2014, 2015) 和皮质-丘脑子网络间时滞 (Breakspear et al. 2006) , 然而这一重要动力学特性尚未在癫痫的发作机理方面进行过深入全面的探讨分析. 特别地, 实验证明 (Meeren et al. 2005) 在自发性失神发作期间皮质与皮质间以及皮质-丘脑回路都存在明显时滞现象. 另外, 耦合神经系统的同步问题是研究脑信息处理的关键 (Jin et al. 2017a, 2017b; Inoue et al. 2003; Frank et al 2010) . 研究表明, 即使在两个远程癫痫发作区域之间也能够观察到异常同步现象, 而远程皮层区域间同步发作的动力学机制仍不清楚 (Meeren et al. 2002, Drover et al. 2010). 基于此, 提出了一个两室时滞耦合的皮质-丘脑网络动力学模型 (图25, Fan & Zhang 2018) , 综合分析了不同回路时滞对癫痫自发发作及同步转迁的影响. 具有固有时滞和耦合时滞的两室耦合皮质-丘脑神经场模型可以由如下表达式描述:

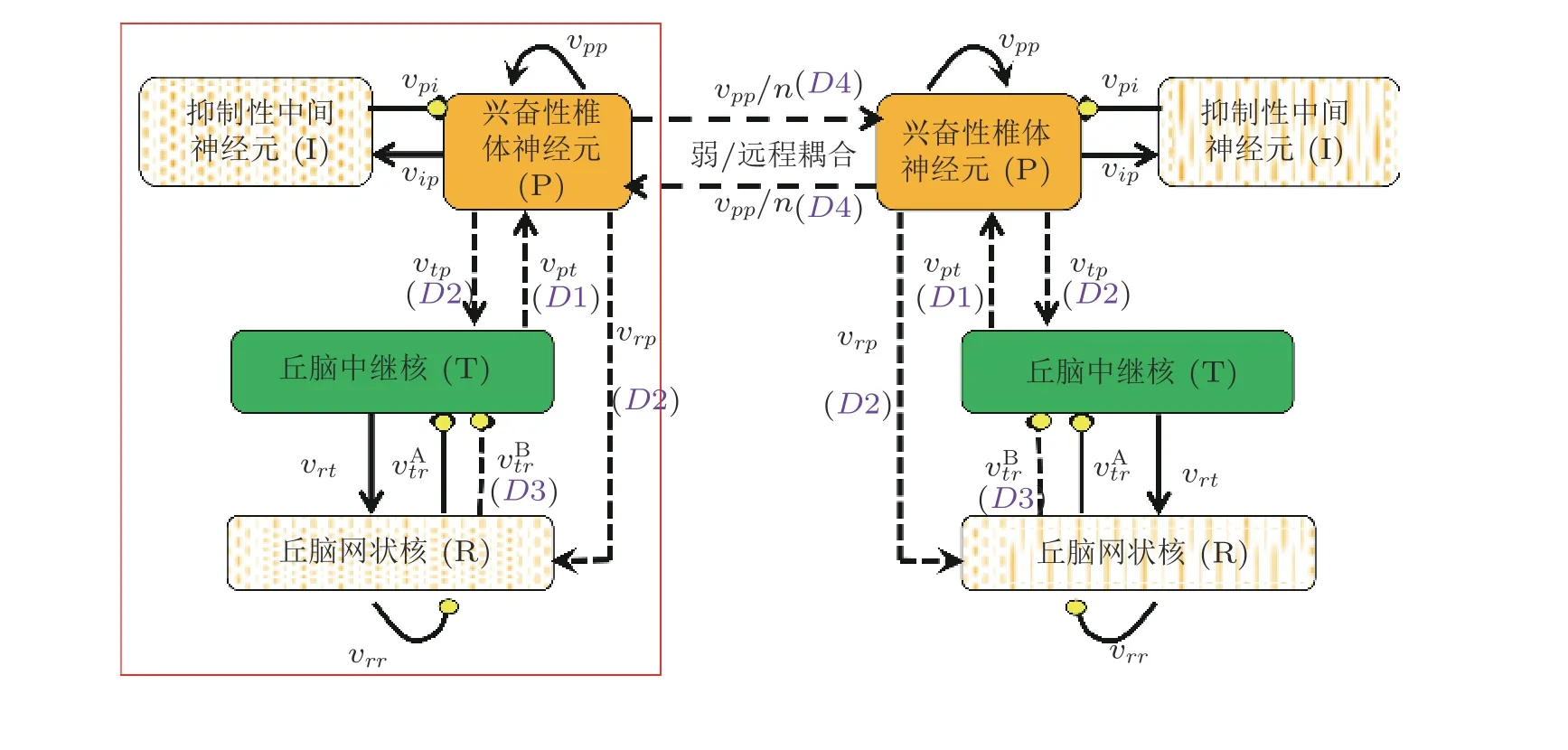
图25皮质−丘脑环路时滞网络动力学模型示意图, D 1为 丘脑中继核到皮质时滞, D 2为皮质到丘脑中继核时滞, D 3为 丘脑网状核到中继核时滞, D 4是耦合时滞 (Fan et al. 2018)

由此可见, 时滞在癫痫的发生发展和终止过程中起着不可或缺的作用, 对癫痫发作调控的综合效果分析为理解癫痫的发作动力学机理和设计可行的非线性调控策略提供重要的理论依据.

4 癫痫平均场网络动力学建模分析与调控

4.1 平均场模型建立及其动力学

平均场模型是基于空间的平均化, 能够把高维复杂的非线性网络动力系统简化为简单的低维系统来处理以减少计算成本, 为大尺度网络动力学建模分析提供潜在途径. 神经系统的平均场模型可以用于描述大脑神经元集群的平均化特性如平均放电率和平均膜电压等. 利用平均场模型预测的皮层脑电波的基本特征以及脑电和空间结构的相干特征等, 都已在实验上得到了证实(Rodrigues et al. 2009, Jirsa & Haken 1996) . 平均场模型可以给出实验中观察到的皮层节律行为的生物物理机制的合理阐释 (Freyer et al. 2011) , 也可以解释皮层-丘脑环路作用诱发异常节律如癫痫失神发作节律 (Marten et al. 2009) 的电生理机制和动力学特征. 基底节作为大脑的深部核团直接或者间接地中继皮层信号到丘脑来调节皮层与丘脑间的信息交互. 研究指出全面性癫痫患者失神发作时基底节网络中核团的功能连接性显著增强. Chen 等 (2014, 2015) 建立了一个皮层-基底节-丘脑环路平均场网络动力学模型, 理论证实基底节对失神癫痫的发作具有双向的调控作用.

4.2 基于皮质−基底节−丘脑环路的癫痫失神发作动力学建模分析与调控

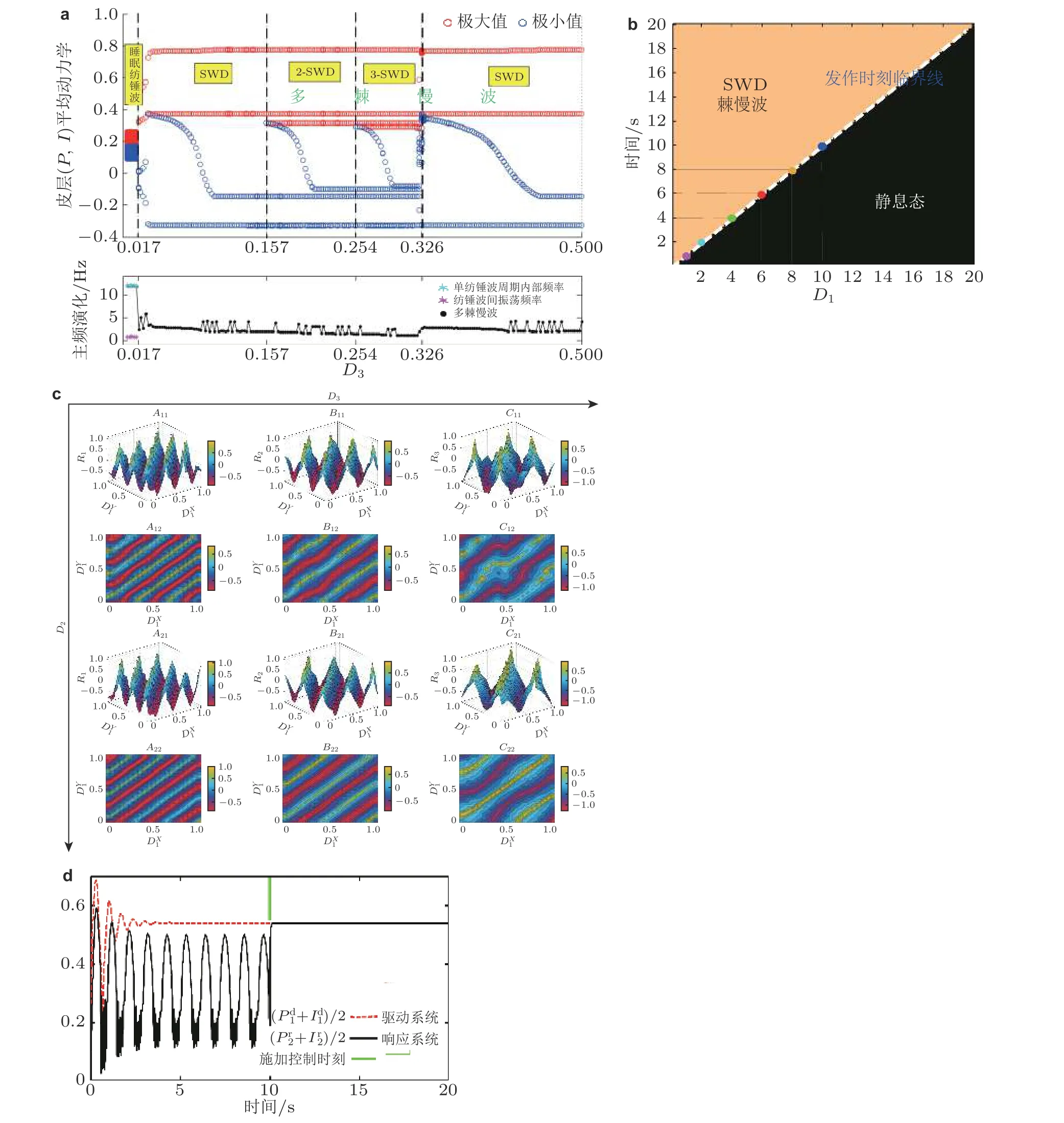
图26(a)皮质平均动力学关于D3 的分岔图, 系统状态连续地从纺锤波振荡 (spindle) 转迁到SWD, 2-SWD 和3-SWD; (b) D1 诱导的SWD 精确发作, D1 与其诱导SWD 的发作时刻呈线性增长关系(白色虚线); (c)随着D2 增加 (向下箭头) 和D3 增加 (向右箭头) , 在三维空间 (D1X, D1Y, R)及其投影平面(D1X,D1Y) (等高线图) 上D3 诱导的SWD (左列) , 2SWD (中列) 和3SWD (右列) 的同步(R1, R2, R3) 演变, 其中发现D2 能有效规范同步发作模式. (d)驱动系统驱动响应系统的癫痫多棘慢波放电终止, 绿线表示控制输入 (Fan et al. 2018)

癫痫的深脑高频电极刺激治疗是一种重建性治疗方式 (Wang & Wang 2017, 2019; Fan et al.2016b) , 不会破坏细胞本身的结构, 它产生的兴奋性或抑制性场作用会产生可逆的功能性毁损,通过调节刺激的强度和频率会改变深脑刺激的作用效果 (Merrill et al. 2005, Hardesty & Sackeim 2007, Jayakar 1993, Miocinovic et al. 2009) , 因此是一种比较理想的癫痫治疗手段. 关于电刺激控制癫痫神经疾病的病态特性, 基于皮质-基底节-丘脑环路系统已经开展了广泛的生物实验研究(Suffczynski et al. 2008, Taylor et al. 2014, Cukiert & Lehtimaki 2017, Paz et al. 2013) , 皮质 (Cortex) 、基底节 (basal ganglia, BG) 和丘脑 (thalamus) 也因此成为深脑电刺激控制神经性疾病如癫痫和帕金森症的主要刺激靶点. 尽管如此, 临床实验证据证实不同的刺激靶点以及不同的刺激策略对癫痫的控制效果有优劣之分, 如何选择刺激靶点和选择有效的刺激策略成为控制癫痫神经疾病的一个重要科学问题. 在先前的研究中, DBS 的靶点往往都集中在单一结构模块, 持久地刺激单一部位会造成特定的物理损伤, 产生副作用, 同时会消耗掉更多的电流. 因此, 针对如何选择更加安全有效且节能的刺激方式进行了深入的研究.

尽管已经证实, 癫痫的失神发作源于皮质-丘脑环路的作用异常 (Sitnikova et al. 2014, 2016) .然而越来越多的证据表明, 基底神经节 (BG) 也参与癫痫的失神发作 (Chen et al. 2014, 2015; Hu et al. 2017) . 特别地, 基底节通过作用于皮质-丘脑环路来调节癫痫的失神发作, 由此形成的皮质-基底节-丘脑环路 (BGCT) 提供了一个理解癫痫失神发作的理论框架. 如图27 所示, BGCT 环路网络动力学模型框架已经成为研究癫痫发作机理的标准模型. 在BGCT 环路中除了各种核团神经元群体之间的相互连接外, 自突触连接 (autapse) , 即神经元到自身的突触连接, 在神经系统中也很常见 (Kim 2017, Wiles et al. 2017, Xu et al. 2017) . 研究表明自突触可能提供了有效的或经济的途径来影响和控制神经元的活动. 另一方面, BGCT 环路基底神经节 (BG) 中的丘脑底核(STN) 在神经性疾病如癫痫和帕金森症起着关键性的调节作用, 然而STN 的自突触动力学从未被涉及. 特别地, 临床证据表明对于耐药性或对手术治疗效果不佳的癫痫患者, STN-DBS 可能是一种有效的治疗手段 (Hu et al. 2018, Vercueil et al. 1998) . 更重要的是, 过去的实验和计算研究表明将合适的DBS 刺激应用于STN 可以抑制失神癫痫的产生.

受以上问题启发, 首先通过在已有的BGCT 模型中引入STN 自突触连接提出改进的皮质-基底节-丘脑 (MBGCT) 环路模型 (图27) , 来研究STN 自突触动力学对癫痫失神发作的作用效果 (Fan & Wang 2018) . MBGCT 环路动力学用平均场模型来描述.

这里特别地引入了一种新的刺激模式即电荷平衡的双相脉冲刺激模式 (CBBP, 见图28) , 来研究STN 自突触调节下CBBP 刺激STN 对皮层癫痫失神发作的控制效果 (Cappaert et al. 2013) .特别地, 当外部刺激应用于STN 时, STN 的膜电压,Vs(r,t), 由下式确定

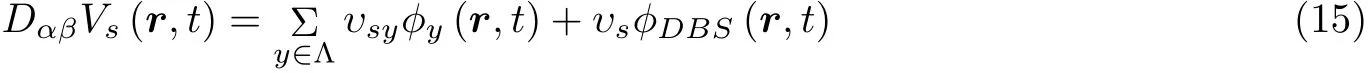
其中φDBS(r,t)是 由刺激电极产生的电场的输入脉冲,υs是刺激电场的强度.

如图28 分别展示了不对称 (AS) 和对称 (S) 的分别具有 (x＞0) 和不具有 (x=0) 相位间期(inter-phase gap, IPG) 的CBBP, 即AS-CBBP-IPG0 (图28(a)) , AS-CBBP-IPGx(图28(b)) ,S-CBBP-IPG0 (图28(c)) 和S-CBBP-IPGx(图28(d)) . 具体可以用下面算法进行

其中

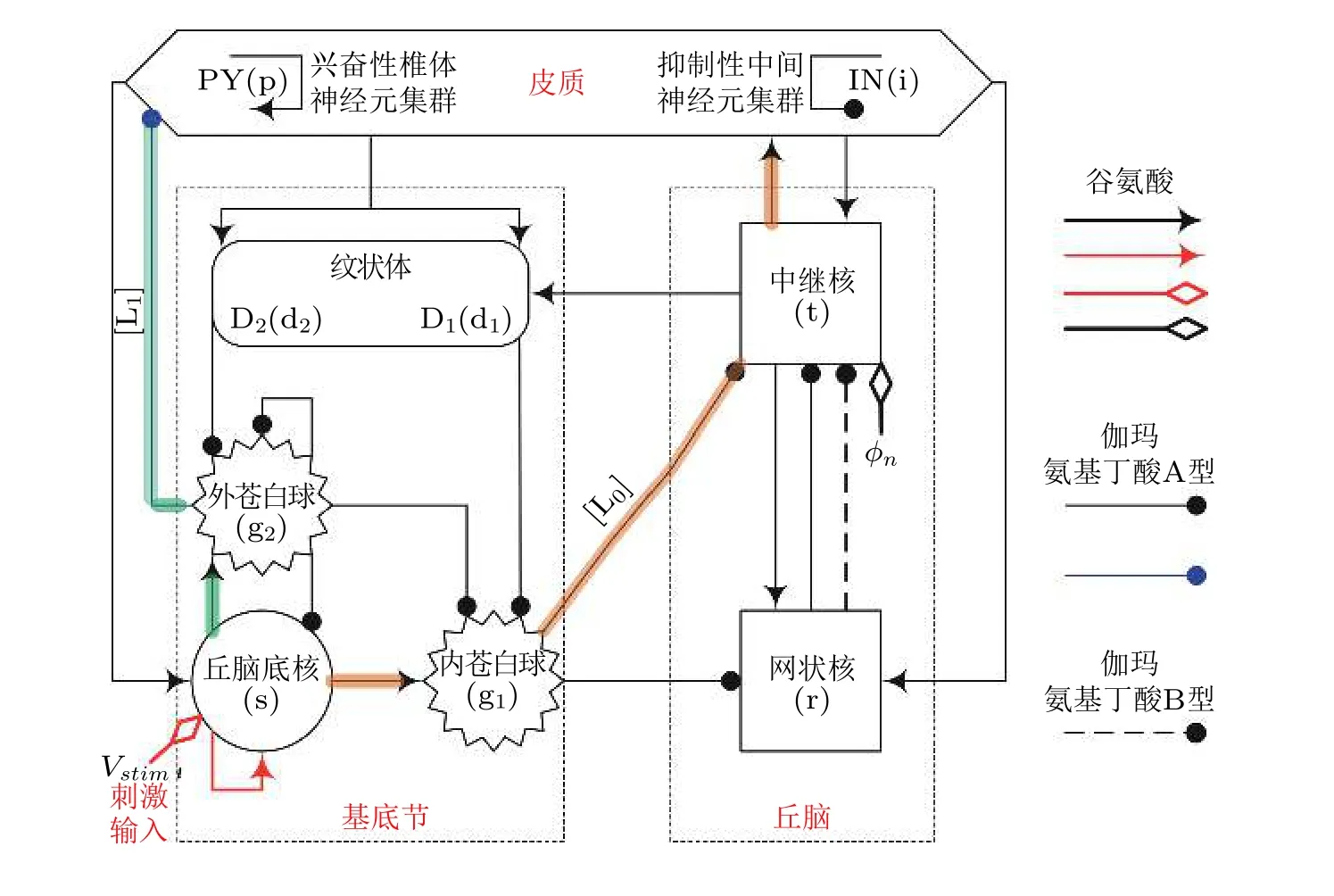
图27皮质−基底节−丘脑环路网络框架图: 皮质由兴奋性椎体神经元(PY)和抑制性中间神经元 (IN)组成; 丘脑由中继核 (TC) 和网状核 (RE) 组成; 基底节由纹状体 (D1/D2) , 丘脑底核 (STN) , 内苍白球 (GPi) 和外苍白球 (GPe) 组成. 箭头代表神经元集群之间的兴奋性投射作用, 带有实心圆端点的射线代表由GABAA (实线) 和GABAB (虚线) 调节的抑制性投射作用. φn代表到TC 的非特定外部输入. 红色箭头代表新引入的STN 自突触作用, V stim为注入的外部刺激干扰. 阴影线分别代表从STN 到皮质的前驱 (L0) 和后驱 (L1) 投射路径 (Fan & Wang 2018)

理论结果证实具有适中相位间期的双相对称脉冲刺激控制癫痫可以取得最优调控效果(图29) , 且丘脑底核自突触可以增强刺激对癫痫的控制效果, 从而从计算角度支持了STN 参与癫痫失神发作的调控机制. 这一结果也为基底神经节 (BG) 参与癫痫失神发作调控提供重要理论支撑.

4.3 基底节调节下失神发作的闭环反馈控制

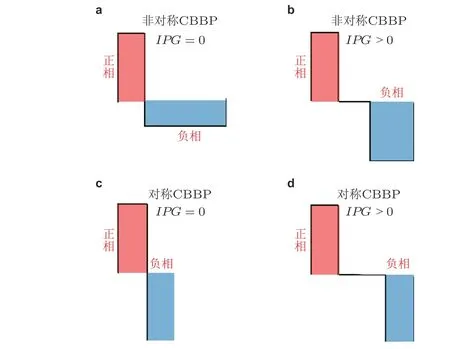
图28具有 (b) (d) 和不具有 (a) (b) 脉冲间期 (IPG) 的电荷平衡的双相脉冲刺激模式, 其中 (a) (b) 为非对称形式, (c) (d) 为对称形式 (Fan & Wang 2018)

尽管已经由实验和以上理论证实了基底节参与癫痫的调节过程, 但为了进一步提高刺激调控癫痫的效果, 这里对皮质-基底节-丘脑 (BGCT) 环路进行了详细的分析. 结果发现基底节(BG) 实际上接收来自皮质与丘脑环路的2 个核团 (PY, TC) 的兴奋性输入信息, 经过BG 分析处理以后接着反馈给皮质与丘脑环路3 个核团 (PY, TC, RE) 的抑制性信号, 以此来调节皮质与丘脑环路的振荡行为. 由此可见, BG 实际上作为一个2 输入-3 输出的2I:3O 反馈调节器存在. 如图30(b)所示, 提出了一个具有2I:3O 反馈调节器的改进的BGCT 环路平均场网络模型 (SBGCT).为了便于探索BG 的调节原理, 这里假定这三个反馈信号为三个特定的输入常数, 由此进一步提出了一个简化的皮质-丘脑环路模型 (RCT, 图30(c)) . 值得注意的是,Pp=Pt=Pr=0代表BG 的异常反馈调节或调节失效. 这种情况下, 一般会引起CT 的异常振荡活动, 如大脑皮层的癫痫样放电. RCT 模型也因此成为目前研究癫痫发生机理的常规模型. 上面的分析也提示, 当BG 调节失效时, CT 环路的PY, TC, RE 三个核团可作为目标核团来进行刺激调控. 这一刺激调控由于假定BG 的反馈信号是恒定常数输入, 所以可称之为开环调控策略. 但是如果刺激调控策略是基于BG 对从CT 获取的输入信息的分析结果做出的, 这种调控方式称为反馈闭环调控策略.

除了刺激效果之外, 在设计刺激模式时还应考虑如何延长电池寿命并潜在地减少副作用. 由于基底节2I:3O 反馈调节器的本质, 这里考虑的是多目标刺激调控问题 (Tass et al. 2013, Guo et al. 2011, Popovych & Tass 2018) . 设计多目标刺激的有效且节能的调控策略, 是研究的热点, 也一直是研究的难点, 因为这需要基于刺激调控神经系统的动力学机理做深刻本质的分析. 目前还缺乏对癫痫的多目标刺激调控策略的研究, 因此对此作了系统全面的研究. 考虑到CRS (coordinated resetting stimulation) 协调重置刺激模式可以交替调控多个核团, 且本身是一种弱刺激策略,同时能够有效地降低网络振子的活动水平 (Bjerknes et al. 2018, Hauptmann et al. 2005, Tass et al. 2009), 可以基于CRS 及其衍生调控方案来优化癫痫失神发作的调控效果.

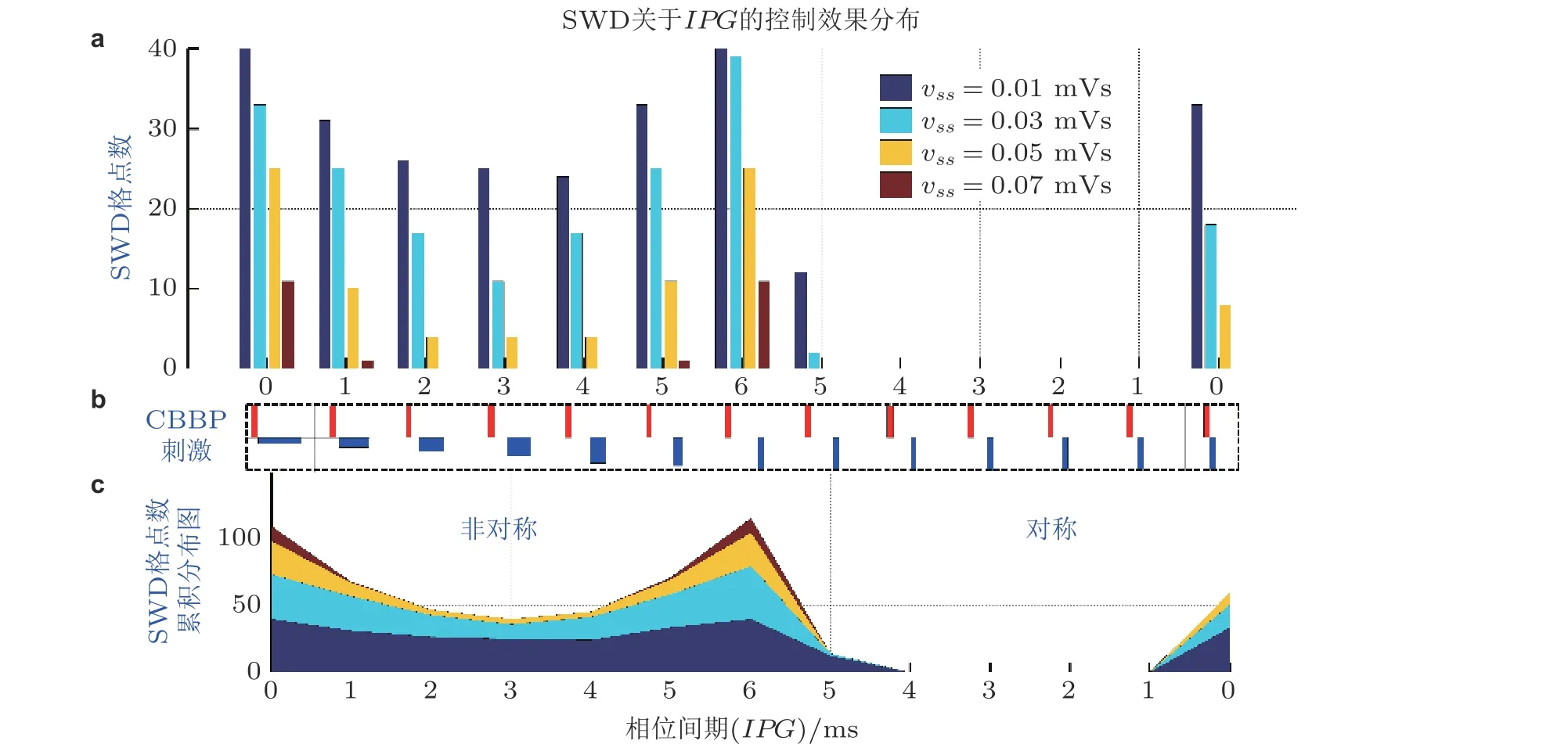
图29具有不同相位间期的双相脉冲刺激以及丘脑底核自突触vss 对SWD 的控制效果. 为了定量观察SWD 的控制效果, 将2D 参数区域进行均匀网格划分, 得到n × n 个网格点, 统计系统显示SWD 的参数网格点数 (Fan & Wang 2018)

图31 给出了几种典型的多目标核团刺激调控模式, 其中发现m:n开与关协调重置刺激具有高效节能等优点. 设计的三目标m:n开与关协调重置刺激的数值算法可以由以下公式来描述(Fan & Wang 2020)

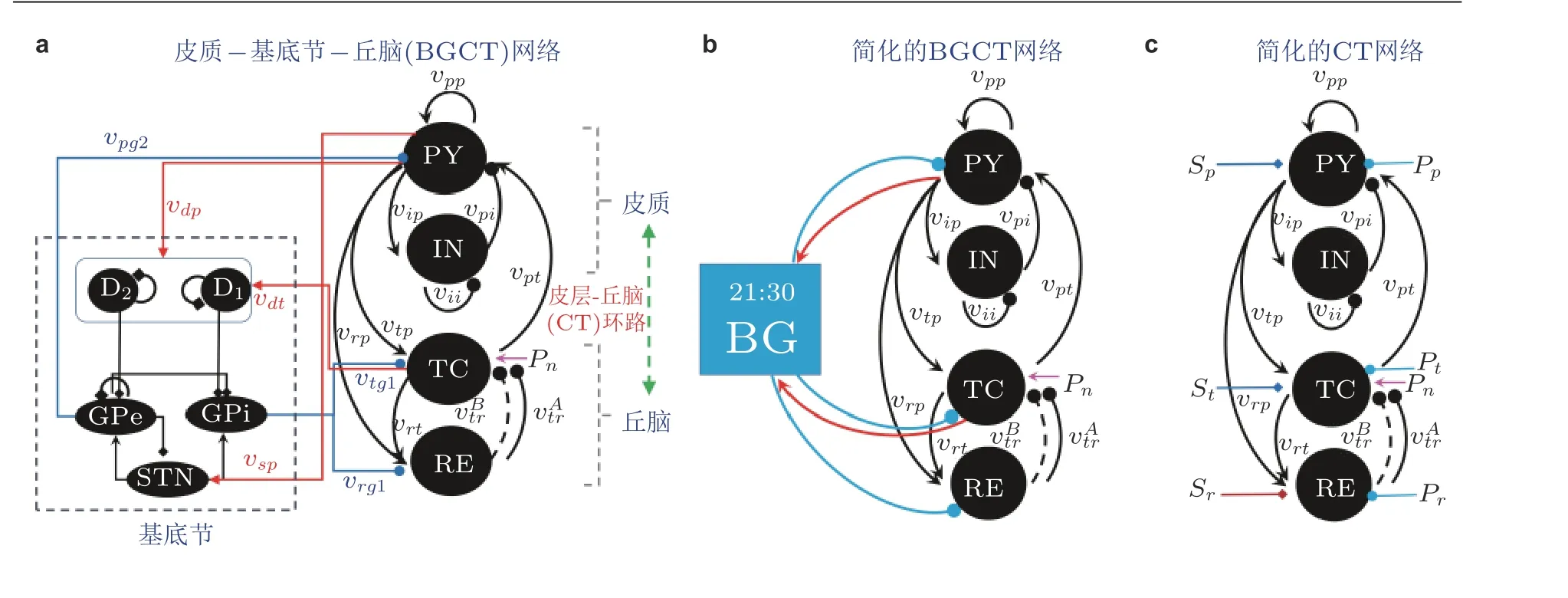
图30(a) BGCT 环路示意图, 由皮层兴奋性锥体神经元 (PY, p) 和抑制性中间神经元 (IN, i) ; 丘脑中继核 (TC, t) 和网状核 (RE, r) ; 基底节中纹状体D1 和D2 型神经元群、苍白球内侧部 (GPi, g1) 和外侧部 (GPe, g2) 、丘脑底核 (STN, s) 组成. 箭头代表由谷氨酸介导的兴奋性突触, 圆圈代表GABAA (实线) / GABAB (虚线) 介导的抑制性投射. 红色和蓝色线条分别表示BG 接收来自皮质−丘脑环路的兴奋性输入和反馈回皮质−丘脑环路的抑制性输出. (b)简化的BGCT 模型(SBGCT), 其中BG 被看作一个2I:3O 调制器, 即接收来自皮质−丘脑环路2 个核团的兴奋性输入和反馈回皮质−丘脑环路3 个核团的抑制性输出. (c)简化的CT 模型 (RCT) , 这里将来自BG 的3 个反馈抑制信号作为皮质−丘脑环路的特定输入常数, P p,Pt,Pr. S p,St,Sr是用于神经调节的外部刺激输入 (Fan & Wang 2020)

其中α决定刺激目标核团,β决定开-关周期.T2=3×T1表 示一个CRS 刺激周期Tcrs,T1=kT0是在一个CRS 周期内应用到每个目标核团的刺激周期数,T0是一个单脉冲或双相脉冲刺激周期,k ∈Z表 示每个CRS 周期中每个目标核团共接收了k个周期的脉冲刺激. 这里应用CRS 刺激到三个目标核团.FIX是取整函数, 即将计算值近似到不超过它的最大整数.Sα(t)是矩形波刺激模式.

从本质上来讲,m:n开关CRS 较经典DBS 的优势主要在于等效调节 (严格讲是降低) 刺激频率, 而刺激强度和脉宽相对不变. 图32(a)为 (RE,TC,PY) 张成的相空间中的SWD 吸引子,显然控制SWD 与改变SWD 的形态密切有关. 这说明可以通过微调SWD 吸引子的形状来进一步优化刺激方案, 意味着分别指向RE,TC和PY的刺激强度和脉冲宽度可能存在差异, 但具体差异需要数值实验进行统计意义上的分析. 为此提出了皮质-丘脑方向可调控的定向刺激 (directional stimulation, DS) 调控策略 (图32) (Fan et al. 2020) , 来进一步优化m:n开关CRS 的调控效果和电流消耗. 这里将RE,TC,PY接收到的刺激强度和脉冲宽度分别用特定方向单位向量V的方向余弦来进行调节计算. 具体计算时, 在 (RE,TC,PY) 的相空间中, 每个核团接收到的刺激强度和脉冲宽度近似成定向刺激强度和脉冲宽度乘以方向余弦值. 结果显示, 在一些特定的方向, 同样在完全控制SWD 的前提下, 定向刺激策略消耗电流较无定向刺激有明显的优越性.

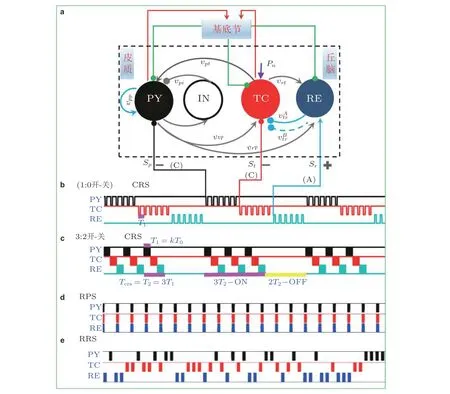
图31(a)在SBGCT 模型上对PY(p),TC(t)和RE(r)施加的协调重置刺激 (CRS) , 其中PY 和TC 接收负相脉冲 (Cathodic, C) 刺激, RE 接收正相脉冲 (Anodic, A) 刺激; (b) (1:0 开-关) CCA-CRS 刺激模式, T0 是在一个CRS 刺激周期Tcrs 内施加单个核团上的刺激脉冲的周期; (c)m:n = 3:2 开−关CCA-CRS: 每进行3 个周期的CRS 刺激 (3 开) 之后附带2 个周期的刺激间歇期 (2 关) , 其中每个周期的CRS (Tcrs = T2 = 3T1) 刺激过程中每个核团平均接收T1 = kT0 时长的脉冲刺激. (d)CCA 规则并行刺激 (regular parallel stimulation-RPS) . (e)CCA 随机重置刺激 (random resetting stimulation-RRS) (Fan et al. 2020)

至今为止, 对电刺激调控大脑活动的动力学机理仍然缺乏, 尤其是在癫痫电刺激调控方面,尚未开展相关的理论研究. 众所周知, 集群编码是神经系统的重要编码方式. 考虑到集群平均放电率 (MFR) 是神经元集群活动的重要特征之一, 基于平均场动力学模型, 通过计算与癫痫失神发作SWD 振荡相关的各个核团的MFRs 平均值 (averaged MFR, AMFR) 以及对应SWD 振荡的临界或触发平均放电率 (triggering AMFRs, TAMFRs) 的动态演化, 首次定量解释了刺激调控癫痫失神发作SWD 的动力学调控机理. 如图33 所示, 通过计算环路神经核团的平均激发率发现,癫痫失神发作时, 可以通过刺激来提高或降低皮质神经元集群的激发率, 使其远离癫痫发作的临界激发率边界曲线而得到控制. 从而从一种新颖的角度给出了临床深脑电刺激调控癫痫发作的理论解释. 这也进一步证实SWD 振荡与特定的平均放电率相关联. 同时具有重要的临床指导意义, 提示可以通过降低或提高SWD 的AMFRs 来双向调控癫痫的失神发作.

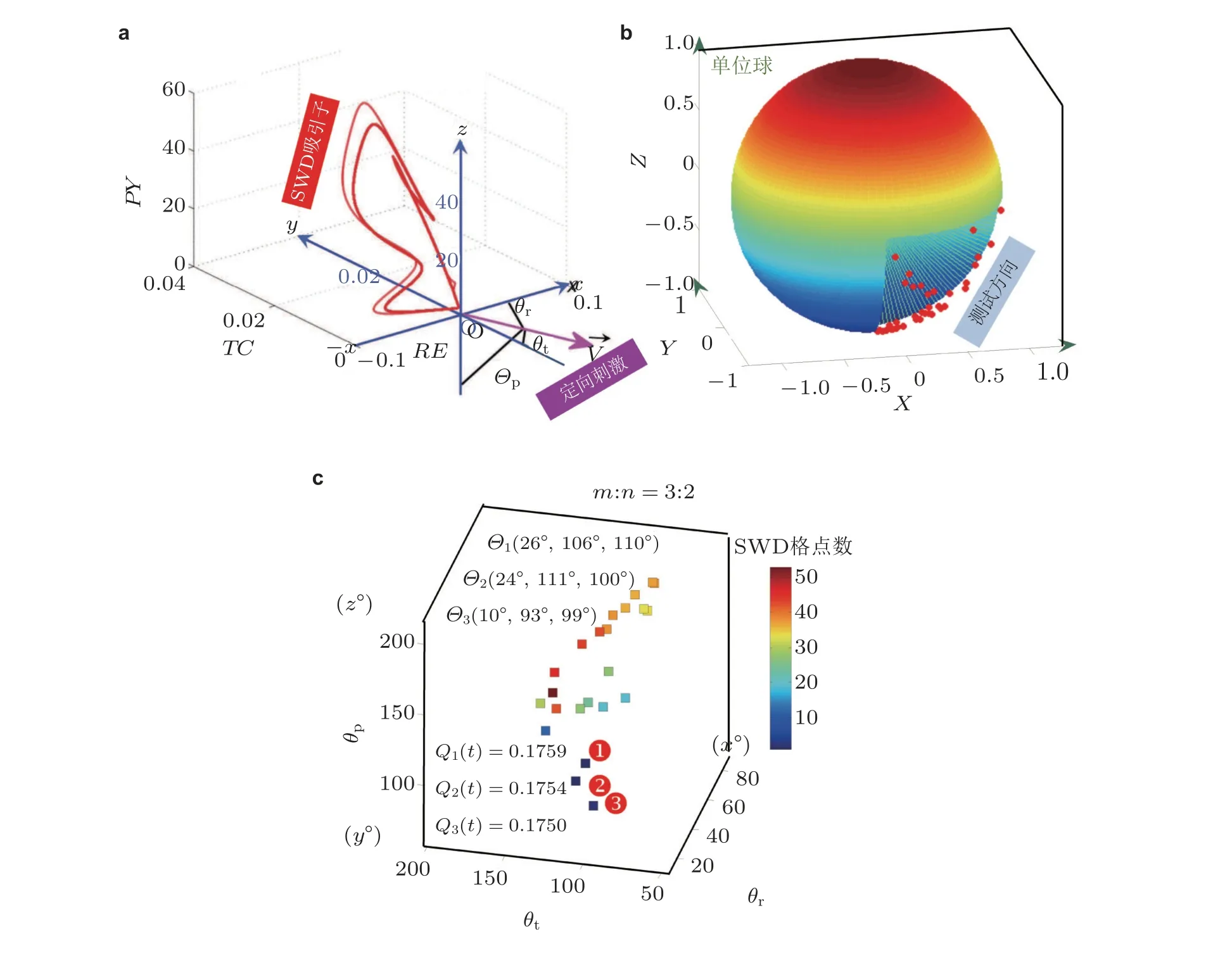
图32皮质−丘脑方向可控的刺激原理 (a) (b) 及其对SWD 的最优控制效果(c). (a)由(RE, TC, PY)生成的三维空间中, 给出了SWD 振荡的吸引子, 并建立了一个原点(0, 0, 0)的笛卡尔坐标系 OXY Z,V 表示有向刺激 (directional stimulation-DS) 的方向, θp, θt , θr分别是有向刺激与三个坐标轴正向的夹角. (b) 笛卡尔3D 空间直角坐标系中的单位球面, 球面上的散点是随机选取的并满足θp ∈(90°,180°), θt ∈(90°,180°),θr ∈(0°,90°), 代表对TC 和PY 的负相 (C,c os θp <0,cos θt <0) 脉冲刺激及对RE 的正相 (A,c os θr ＞0) 脉冲刺激. (c) 3:2 开−关CCA 有向刺激 (CCA-DS) 对SWD 的控制效果, 其中标记①②③表示取得最好控制效果的刺激方向角、SWD 参数格点数和相应的电流消耗 (Fan & Zheng 2020)

然而开环刺激模式需要消耗更多的电流, 且持久刺激能够对脑皮质产生损伤等副作用. 目前基于闭环控制的神经调控策略得到广泛研究, 但对癫痫的闭环调控策略关注很少. 基于癫痫发作的BGCT 环路机制, 特别是考虑到BG 对CT 环路癫痫发作的闭环调节原理, 设计了一种BG 调节异常情况下基于需求的闭环反馈控制方案 (Fan & Wang 2020, Dumpelmann 2019)

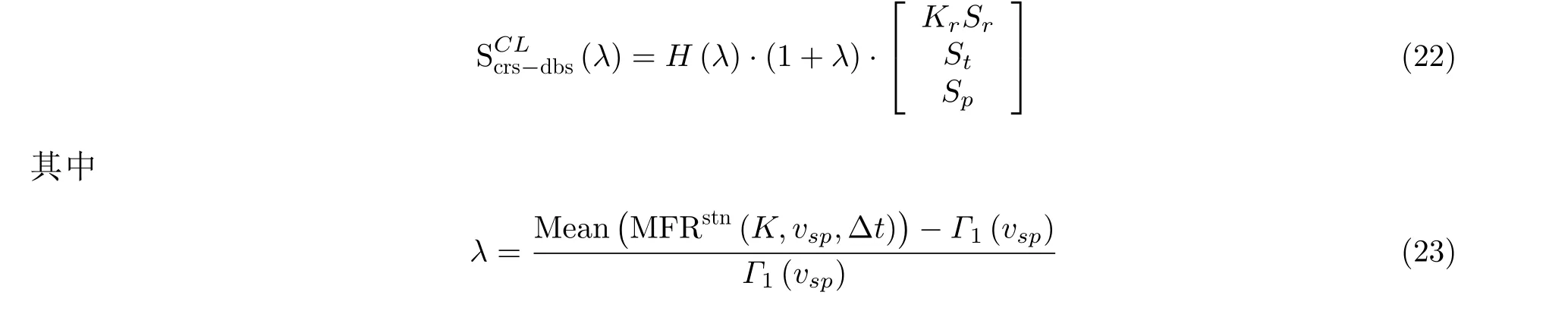
H是Heaviside 函数,Γ1(vsp)对应SWD 的TAMFR, 用来及时触发神经刺激器. 1+ λ 是依赖于时空的控制增益. 当STN 的AMFR 超过TAMFR 时, 闭环神经刺激器开始工作, 将其AMFR 推出TAMFR 确定的SWD 区域外, 从而消除SWD 振荡. 特别地, 如图34 可见, 在完全控制SWD 的前提下, 闭环刺激的总电流消耗明显小于开环刺激. 这一策略有效融合了癫痫的解剖结构、电生理实验和理论方法, 对临床应用提供了有价值的理论参考.

5 癫痫数据驱动的神经元群网络动力学建模分析与调控

临床癫痫病灶精确定位和控制癫痫发作网络的关键节点选择等都还缺乏有效策略, 局灶性癫痫发作传播及其调控仍缺乏动力学的理解. 因此最后我们考虑基于真实癫痫临床数据进行癫痫的统计建模及其动力学机理建模分析.

5.1 神经元群模型建立及其动力学

从动力学角度对癫痫生理特性进行建模分析, 可能为癫痫的潜在动力学机制提供新的见解.为了模拟真实癫痫脑电, 目前常用的动力学模型为基于集总参数方法建立的神经元群模型(Wendling et al. 2000, 2016) , 它实际上是将神经元集群建模为一个非线性振荡器, 用来生成EEG 信号. 集总参数模型是对特定的神经元细胞组成的集群整体特性的建模, 它反映了不同神经元子群以及神经元子群内部之间的相互联系. 集总参数模型主要由两种神经元子集群组成 (如图35 所示) , 即兴奋性椎体神经元子集群 (e) 和抑制性中间神经元子集群 (i) . 每种神经元子集群可以通过微分方程来表达其动力学行为

在图35 中,he(t),hi(t)是线性模块, 分别表示将动作电位的平均脉冲密度转换为平均突触后兴奋性细胞膜电位(EPSP)和抑制性细胞膜电位(IPSP)的转换函数, 具体形式为

S(v)是非线性模块, 它将一个神经元集群的平均膜电位转换为动作电位的平均脉冲密度 (平均发放率) ,S(v)具体用Sigmoid 函数来描述, 其表达式如下

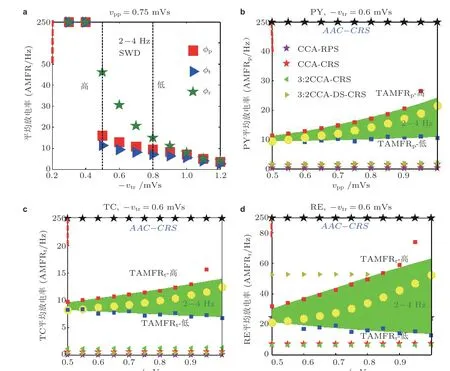
图33电刺激调控SWD 的动力学解释. (a) PY(“■”), TC(“►”), RE(“★”)的AMFR 随着-vtr 的增大而降低. 两条虚线之间的区域表示的是典型的2 ～ 4 Hz 的SWD 振荡区域, 两条虚线分别对应着-vtr 高和低2-4Hz 的SWD 触发平均放电率(TAMFR); (b)(c)(d)在AAC-CRS(黑色★), CCACRS(红色★),CCA-RPS(紫色★), 3:2 开−关CCA-CRS(◄), 3:2 开−关CCA-DS-CRS(►)以及控制组(○)下, PY, TC, RE 的AMFR 与对应-vtr 的高 (红色■) 和低 (蓝色■) TAMFR 随着vpp 的增大的演化图. 图(b)到图(d)中绿色区域表示由-vtr 确定的典型2 ～ 4 Hz 的SWD 振荡区域 (Fan et al. 2020)

式中, 2e0是 转化后的最大发放率, 即最大平均脉冲密度.v0是 对应于发放率为e0的后突触电位,r是Sigmoid 转化函数的陡峭度, 它能够决定转化函数的弯曲程度.p(t)表示远处或邻近神经元集群对该神经元集群的兴奋性输入, 具体模拟时采用的是兴奋性输入噪声即高斯白噪声.

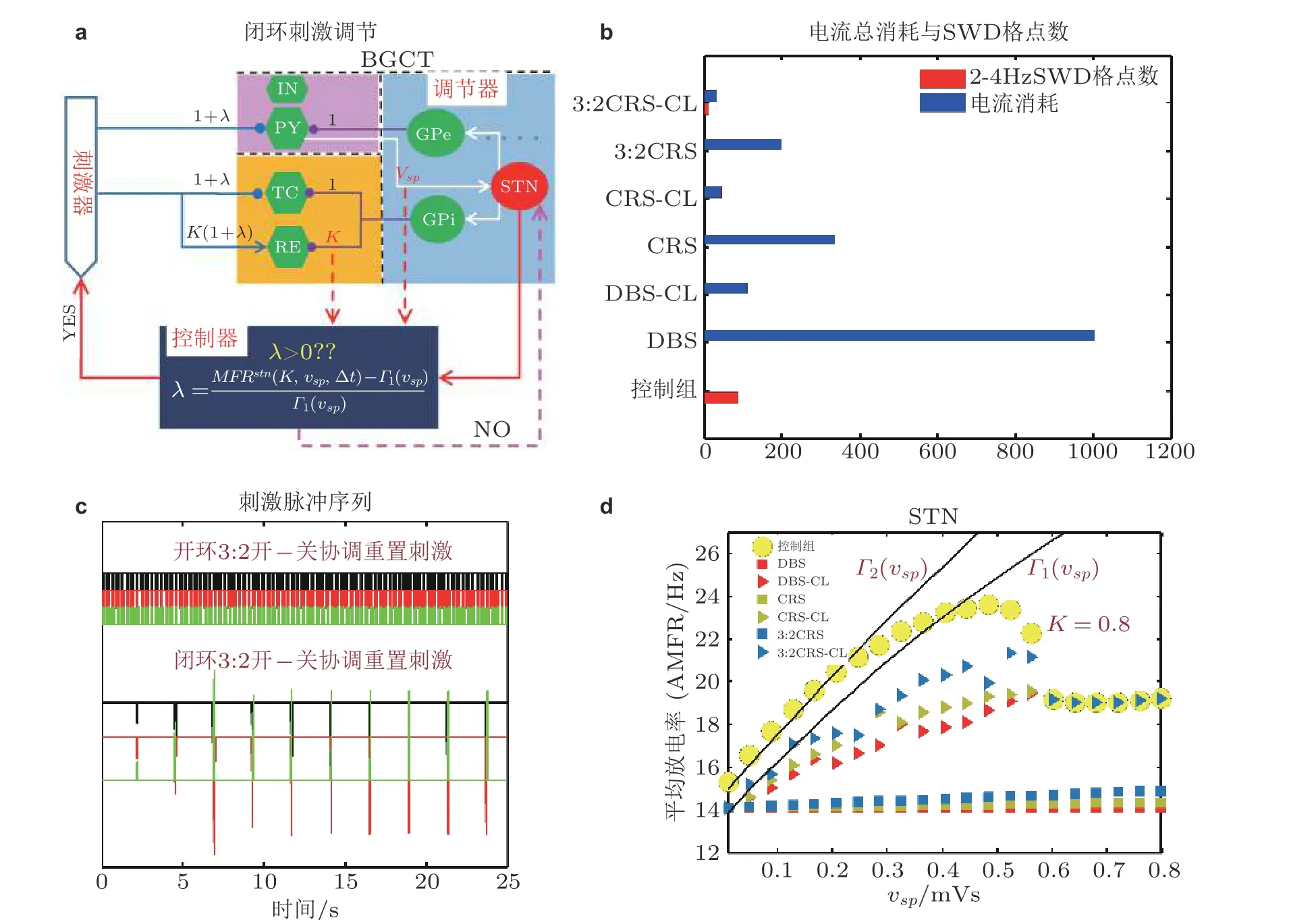
图34(a) 基于STN 的TAMFR 设计的闭环刺激策略, 其中包括了调节器 (基底节) , 控制器和刺激器;(b)不同刺激模式对SWD 的控制效果和电流消耗柱状图. (c) 开环和闭环3:2 开−关CRS 刺激脉冲序列图; (d)常规深脑刺激 (DBS) , 闭环DBS (DBS-CL) , 协调重置刺激 (CRS), 闭环CRS(CRS-CL) , 3:2 开−关CRS 和闭环3:2 开−关CRS (3:2CRS-CL) 等六种不同刺激模式以及无刺激时 (控制组) STN 的AMFR 随着 vsp 的 变化趋势, Γ1和 Γ2为GPi 作用下确定的低触发TAMFR 随着 vsp增大的演化图(Fan & Wang 2020)

C1,C2,C3,C4表 示神经元集群的平均突触连接数, 其中C1,C2表示兴奋性椎体神经元集群回馈环上的平均突触连接数,C3,C4表 示抑制性中间神经元集群回馈环路上的平均突触数.C1表示前馈神经元到兴奋反馈环中的树突的突触数目;C2与兴奋反馈环到前馈神经元的树突之间的突触数目成比例即C2=0.8C1;C3为 前馈神经元到抑制反馈环中的树突的突触数目, 与C1成比例, 即C3=0.25C1;C4与 抑制反馈环到前馈神经元的树突之间的突触数目成比例, 有C4=C3.

注意, 每个转换函数he(t)和hi(t)都可以引出一个如下形式的二阶常微分方程

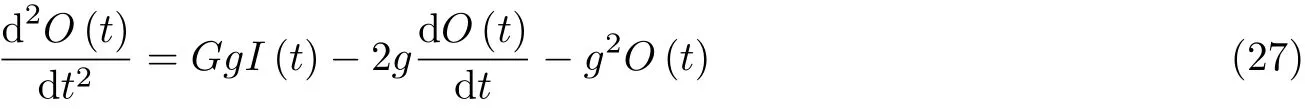
其中I(t)是 输入信号,O(t)是 输出信号, 对于兴奋性和抑制性集群,G分 别取A和B,g分别取a和b,因此, 神经元群模型集总参数的动态特征由以下三个二阶微分方程表示

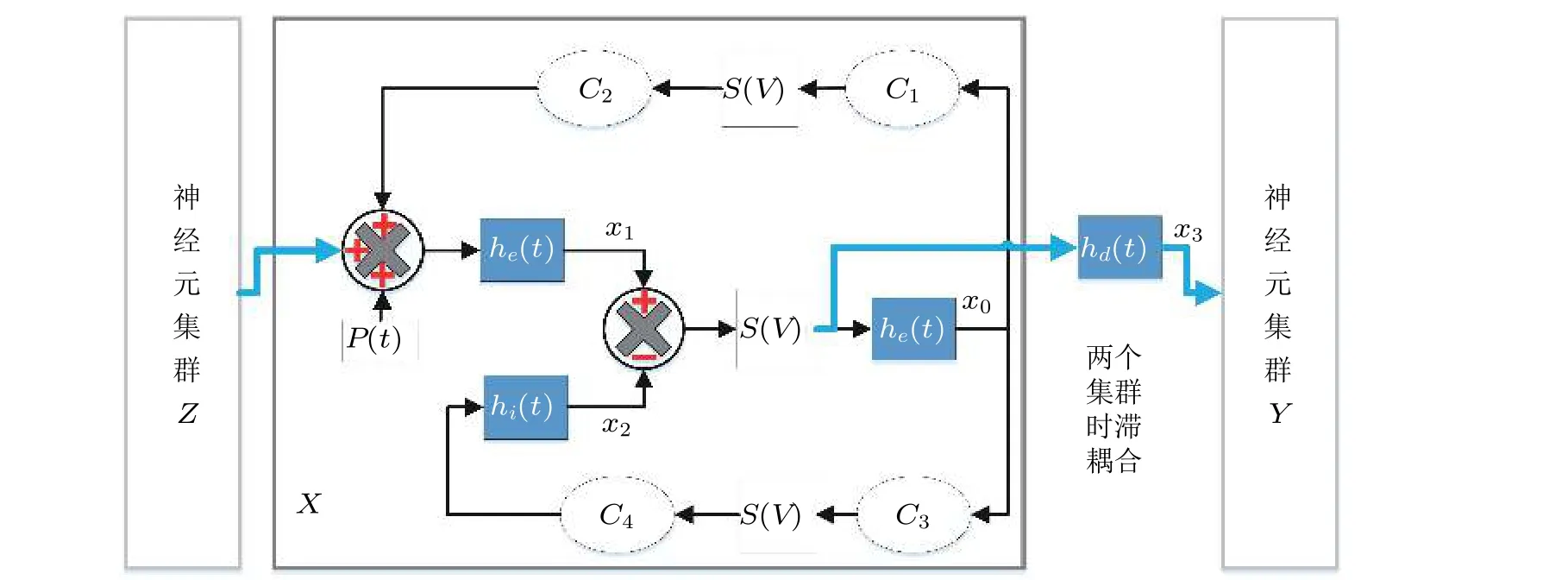
图35时滞耦合神经元群模型结构. 虚线矩形框展示了单个神经元群模型X 的内在动力学机理, Y 和Z 与之类似. he,hi,hd分别是兴奋性突触后电位EPSP 和抑制性突触后电位IPSP 的线性转迁函数, S (v)是 非线性转迁函数, C 1,C2,C3,C4 表示关联突触的平均数量. p (t)是高斯白噪声, 是对环境影响的建模. x0 表 示中间神经元EPSP 转迁函数 he 的 输出, x1表示锥体神经元EPSP 转迁函数he 的输出, x2 表 示锥体神经元IPSP 转迁函数 hi 的 输出, x3表 示EPSP 转迁函数 hd的输出.

5.2 局灶性癫痫的病灶定位及其调控

在临床上, 局灶性癫痫表现为局部脑区阵发性异常放电. 癫痫病灶的术前精确定位是难治性癫痫患者手术治疗的关键一步, 然而较高的手术失败率表明病灶的精准定位仍然是相当棘手的问题. 作为临床诊断的重要依据, 癫痫术前会做大量影像学检查. 当影像学数据无法对癫痫病灶给出统一结论时, 将采用侵入性的监测手段如立体脑电图 (SEEG) , 它能采集颅内高信噪比脑电信号且直达任意解剖区域而被视作病灶定位的“金标准” (Cossu et al. 2005) . 但是, 病灶的识别主要依靠电生理医师的视觉分析, 缺乏量化标准, 不可避免地存在主观性和不确定性 (Harvey et al.2008) . 鉴于此, 可以致力于建立长时程立体脑电的分析框架 (Yang et al. 2018) , 对癫痫病灶进行准确定位.

癫痫被认为是网络异常的结果, 近年来国内外学者已经提出了许多脑连接的计算方法, 旨在从网络的角度去认识和理解大脑功能性活动 (Bartolomei et al. 2008, Panzica et al. 2013) . 研究病灶的切除对病态网络的改良作用也是目的之一. 采用如下的方向传递函数 (Kaminski et al. 2001,Astolfi et al. 2008) 进行动态因果的效应网络统计建模

出度是效应网络的重要拓扑特征之一, 出度较大的节点在网络中所起的作用被证实同癫痫病灶在癫痫发作中起到的作用极其相似 (Wilke et al. 2011) . 因此, 选取出度作为分析效应网络的主要指标. 但是, 不同阶段包括发作间期、发作前期和发作期的网络的演化及差异没有被系统性地揭示. 利用包含各个阶段的长时程立体脑电数据, 来揭示网络特征的变化过程, 分析连接模式的差异, 进而对癫痫病灶进行定位. 如图36 给出了一位局灶癫痫患者的统计分析结果, 发现各个通道的出度随时间变化而变化, 发作间期、发作前期和发作期的出度分布有着明显的差异(图36(a)(b)) , 但是阶段内的出度分布相对稳定, 特别是出度较大的通道在大部分时间内保持着较高的出度. 其中通道E04 在发作间期和发作前期都是出度最大, 决定着整个网络的状态. 而在癫痫发作期通道J14 和M08 的出度急剧增大, 替代E04 成为网络的关键点. 临床监测也证实了这一点, 在发作间期E04 通道记录到大量间歇性棘波. 电生理医师认为异常同步放电由E04 传播至E、M 电极的局部触点, 进而影响更多脑区. 电极间的相对位置和手术切除区域在图36(c)(d)中标出, 而且理论上的致痫通道都在切除范围内. 良好的手术效果进一步证实了该方法的准确性和有效性.

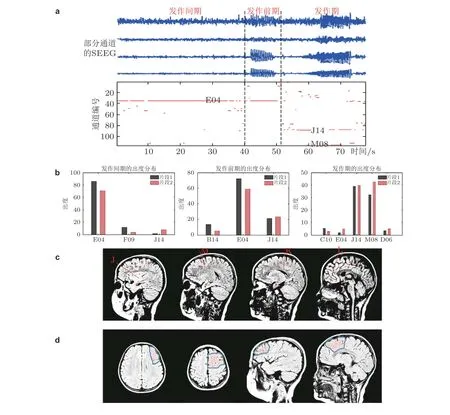
图36选取的癫痫患者病灶定位的计算结果. (a)上半部分是部分通道的SEEG 数据, 下半部分是对应时刻每个通道的出度变化 (为了突出出度较大的通道, 仅将出度大于30 的用红色点显示); (b)发作间期、发作前期和发作期的出度分布 (仅列举出度较大的通道) , 不同的片段计算的结果类似,表明结果的可重复性; (c)电极位置的示意图; (d)手术切除区域的示意图(Yang et al. 2018)

棘波是癫痫患者异常脑活动的重要生物标识. 可以利用神经元集群网络模型, 分别模拟切除前、随机切除和准确切除病灶三种条件下的电活动, 统计棘波的发放密度. 切除前的仿真表明,发作间期存在间歇性的棘波放电, 而发作期会产生持续的、高密度的棘波 (图37(b)) . 该结果与临床记录基本吻合 (图37(a)) , 初步说明发作期的脑网络更容易激发棘波的产生. 图37(c)(d)通过随机切除和准确切除病灶的仿真, 进一步研究切除手术对棘波发放的影响. 与随机切除相比,切除病灶能有效地降低棘波的密度 (图37(e)) , 特别是发作期. 事实上, 临床的切除范围比理论区域稍大, 能进一步减少棘波的产生, 降低癫痫发作的频次甚至实现无复发. 如图37(f)所示, 切除前的仿真结果显示发作间期存在持续性的棘波放电, 而发作期仅有零星的棘波. 在病灶准确切除的条件下, 各个阶段的棘波放电都得到有效抑制. 说明了发作间期的脑活动可能存在诱发癫痫的潜在因素.

尽管已经找到出度较大的通道, 并发现这些通道与癫痫病灶密切相关, 但是从发作间期到发作期的转迁可能不仅仅是由于出度分布的变化, 与之伴随的可能还有网络的结构和功能更深刻的改变. 局灶性癫痫发作时伴随着致痫网络病态信息流的发生、发展和终止 (Tang et al. 2020,Kramer et al. 2012, Palmigiano et al. 2017, Battaglia et al. 2012) . 把握病态信息流方向和强度的准确性, 决定了致痫效应网络重构的准确性和有效性, 进而影响癫痫病灶定位的精确性. 尽管方向传递函数在癫痫的病灶定位方面具有较大优势, 但是因不能很好地区分直接因果和间接因果而不可避免地引入“虚假因果”, 因此方向传递函数在辨识癫痫病态信息流的演化方向和强度方面仍具有一定的局限性. 鉴于此, 可以继续采用新的统计分析方法来确定不同信号通道之间的因果关联 (Fan et al. 2021) , 从而尝试辨识癫痫病态信息流的演化方向, 并基于信息流方向的辨识结果构建癫痫效应网络模型 (图38) . 但是, 如何准确捕捉病态同步信息流的演化过程仍然是一个棘手的科学问题, 需要建立更加合理的因果关系度量和同步度量来评估癫痫网络中两两节点之间的信息流有向传播强度, 从而确定一个带权有向的癫痫效应网络. 基于Quiroga 等 (2002) 提出的测量事件发生的同步性和时间延迟模式的简单快速方法, 可以对局灶性癫痫患者数据进行了统计建模和癫痫效应网络构建来进行癫痫病灶定位, 特别是基于构建的效应网络来寻找完全控制癫痫发作的关键网络节点, 同时分析计算的网络控制关键节点与临床确定的病灶节点的对应关系 (Fan et al. 2021) . 具体地, 对于网络中的任意两个节点i和j, 假设其对应的时间序列为xi和xj, 根据Quiroga 等 (2002) 提出的因果与同步统计方法可以计算出时间点n处的同步增长率dQτ(n)和 因果水平变化率 dqτ(n). 用aij(n)来 表示在时间点n处节点i对节点j的带权有向作用强度, 其中也包含了两个节点之间的同步水平信息, 简述为下式定义 (Fan et al. 2021)

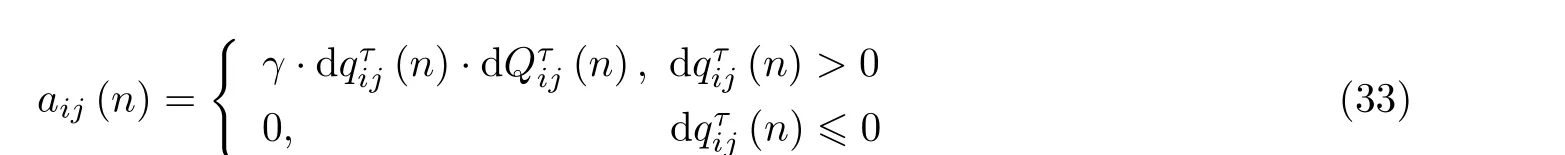
其中γ为放大系数.

对于癫痫来说, 不仅要精确定位致痫灶, 考虑到癫痫发作是一个脑网络事件, 会随时间和空间动态演化, 所以还应考虑基于癫痫网络如何选取控制节点实现癫痫发作的有效控制. 当癫痫有向加权网络被确定下来之后, 想要确定癫痫灶或者控制癫痫发作, 就要分析网络中节点的重要性, 以便找到可以控制网络演化的关键节点. 假设完全控制癫痫发作的关键节点并不一定完全是网络的度最大的节点 (根据前述可知出度最大的节点与临床确认的病灶节点相吻合), 因为即使是控制致痫网络度最大的节点, 仍然有治疗失败的临床案例. 为了找到控制网络的所有关键节点, 特别采用结构可控性理论方法对癫痫效应网络进行分析, 这是因为构建的癫痫效应网络中节点之间的作用强度是随着时间动态变化的. 脑网络动力学系统可以由下面这个通用的状态方程来表示

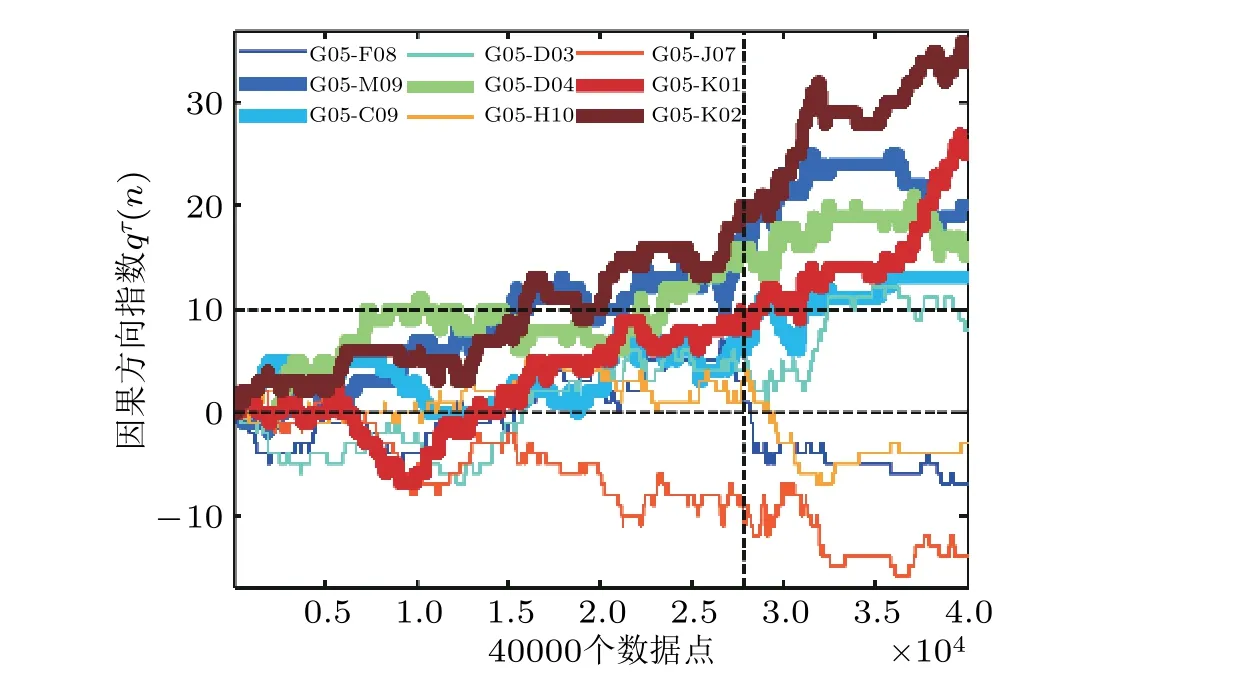
图38选取的癫痫患者 (见表1 中编号为1 的病人) 大脑通道G05 对其他9 个通道信号 (F08, M09, C09,D03, D04, H10, J07, K01, K02) 的因果性随时间的演化. 垂直虚线标出了癫痫发作位置, 水平虚线分别标出了因果阈值 qτ(n)=0 和 qτ(n)= 10 的位置. 选取 qτ(n)=10 作为阈值来表示显著的因果关系. 其他每个通道与其余通道的信息流因果关系分析类似 (Fan et al. 2021)

这个方程中的f和h往往是非线性的, 甚至是不可测的函数, 因此十分复杂. 尽管大多数真实的系统都是以非线性的形式演化的, 但是非线性系统的可控性在许多方面都是结构类似于线性系统的 (Brogin et al. 2020, Liu et al. 2011, Wang et al. 2012, Slotine & Li 1991) . 因此, 对非线性系统的研究可以简化为对典型的线性动力系统的研究. 设原系统简化后的线性动力系统如下

癫痫网络的可控性主要是指通过调控网络个别关键节点来达到抑制整个网络癫痫活动演化的效果. 考虑结构可控性是因为假设网络节点间连接权重发生波动时在一定程度上并不影响网络的可控性. 如果癫痫网络是一个结构可控的系统, 则要么癫痫网络本身是可控的 (可控性矩阵满秩) , 要么在某些连边权值发生轻微变化后变为可控的, 而在连边权值可能发生较大变化时仍然是可控的. 在网络可控的前提下, 关键是寻找能够控制整个网络的最少数量的关键节点. 针对这个问题, Liu 等 (2011) 基于网络二分图的最大匹配集方法确定了最小非匹配集, 位于最小非匹配集中的节点就确定为可以实现控制网络的最少数量的关键节点 (最少输入定理) . 按照可控性条件, 分别对这几个非匹配节点进行控制输入 (即确定系统的输入矩阵B) 就可以使得可控性矩阵满秩. 以图39(c)为例, 绿色箭头勾勒出了网络的四条匹配路径 (Wang et al. 2012, Fan et al.2021) :{1→5→2→3},{4→10},{6→9},{8→7}(事实上已经是数量最少的路径数量) , 因此该网络的最大匹配集为{5, 2, 3, 10, 9, 7}, 相应的不匹配集为{1, 4, 6, 8}. 由于网络的路径不唯一,因此不匹配集也不是唯一的, 但是最小不匹配集的数量是固定的.

为了验证以上选取网络关键控制节点方法的有效性, 可以基于数据的因果和同步度分析得到的不同节点的作用强度和神经元群网络模型构建一个时空扩展的耦合网络动力学模型, 来分析选取的关键节点对癫痫网络的控制效果. 图40(a)是患者原始的EEG 信号; 图40(b)显示在对计算的关键网络控制节点进行刺激扰动后, 图40(a)中出现大量棘峰的通道基本都被抑制, 表明整个网络被有效控制; 而图40(c)显示当刺激的节点为非计算的关键网络控制节点时, 通道的棘峰只是略微减少, 发作特征依然很显著. 这说明施加刺激扰动以控制网络状态时, 对节点的选择有较为严苛的要求, 进一步说明了所用方法确定网络关键控制节点的有效性. 图40(d)则是在模拟时去掉了计算的四个关键网络节点通道 (临床上对应病灶脑区的手术切除) , 可以看到其效果与图40(b)类似, 各通道棘峰出现的情况得到较好地消除.

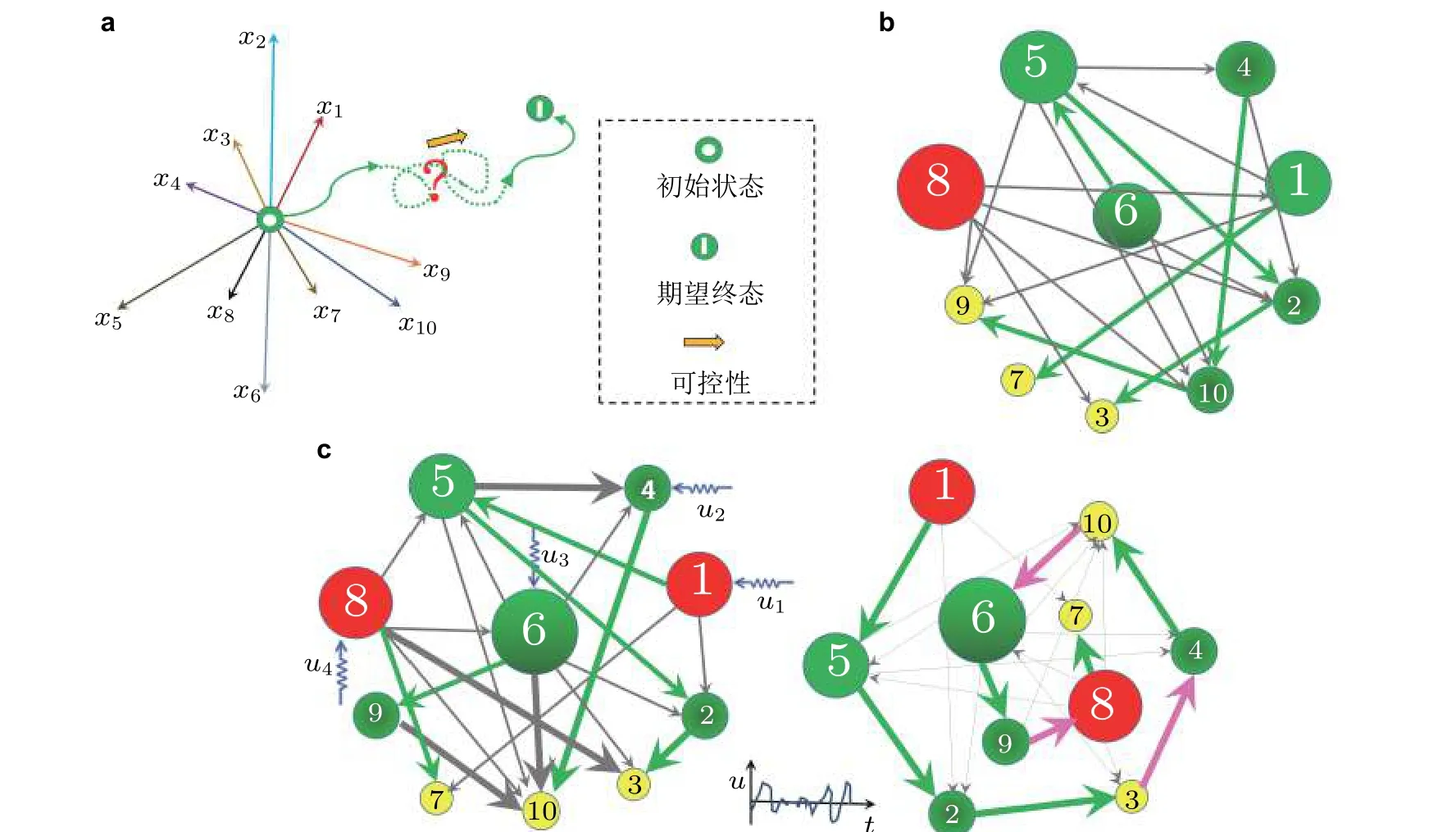
图39基于多通道信息流因果关系分析 (见图38 ) 进行癫痫发作的效应网络构建: 基于表1 中编号为1 的患者数据的因果关系与同步度分析构建的有向加权网络, 这里将每个通道视作一个网络节点 (10 个通道对应10 个节点, 1-F08, 2-M09, 3-C09, 4-D03, 5-D04, 6-G05, 7-H10, 8-J07, 9-K01, 10-K02) . (a)10 个通道EEG 信号假设为癫痫脑动力系统中的10 个变量 x1,x2,...,x10, 从初始状态出发, 网络在癫痫发作间期的状态(b)和癫痫发作期的状态(c)可以通过控制到达任意预期的最终状态 ((a)中向右的黄色箭头) , 这个控制为对无匹配节点 (如: 节点1, 4, 6 和8, 是针对(c)癫痫发作期计算所得) 的输入刺激扰动 u(t)=(u1(t),u2(t),u3(t),u4(t)). (b)和(c)左侧的网络呈现了多种形态的度分布, 节点大小表示网络的出度, 黄色的节点只有入度, 箭头的粗细表示因果性的大小(只有 q(n)＞10才会被绘制出来) . (c)右侧图展示了所有匹配路径 (由绿色箭头标出) , 通过粉色的箭头被依序连接, 其他连接用浅灰色表示 (Fan et al. 2021)

接着对表1 中其他9 个局灶性癫痫患者进行癫痫发作网络的关键控制节点计算, 并与临床定位的病灶节点进行对比. 从表1 可以观察到, 计算的关键网络控制节点集与临床报告定位的病灶节点集之间差异较大, 但对大部分病人两个节点集交集非空, 这意味着完全抑制癫痫发作网络可能除了不仅要控制临床确认的病灶点外, 在癫痫临床症状无法得到缓解时, 计算的关键节点可能就成为潜在的候选节点, 即可能还需要调控病灶点周围节点, 来协同实现对整个网络的控制.特别地, 对第3, 6, 9 号患者来说, 完全抑制癫痫发作需要比临床定位节点数更少的关键节点, 这种情况下可以减少手术电刺激的电流消耗同时减少大脑损伤. 这一新颖的理论结果可能对局灶性癫痫患者的病灶术前评估提供重要的参考价值.

6 总结与展望

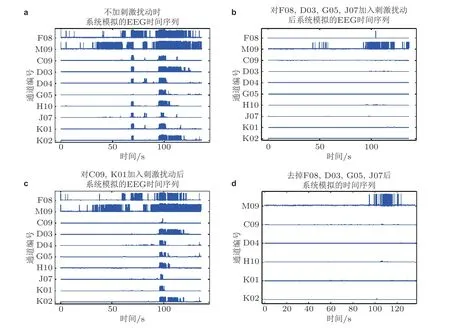
图40数值模拟效果. (a)表1 中编号为1 的癫痫患者原始EEG 时间序列; (b)对计算所得的关键控制节点F08, D03, G05, J07 进行刺激扰动后模拟的时间序列; (c)对任意两条非病灶通道 (C09,K01 为例) 进行刺激扰动后模拟的时间序列; (d)移除时间序列中的病灶通道F08, D03, G05,J07 信号后模拟的时间序列 (Fan et al. 2021)

本文基于癫痫的解剖电生理实验和临床特征, 分别从癫痫海马网络DG-CA3 环路和皮质-基底节-丘脑环路系统的神经元网络模型、神经元群模型以及平均场模型动力学角度, 梳理了国内外研究进展, 重点介绍了本文作者在癫痫非线性动力学建模分析与调控研究中的若干进展. 癫痫非线性动力学建模与调控研究属于新的交叉学科研究, 对理解大脑神经疾病的工作原理和临床应用都有重要的理论参考价值.

尽管癫痫发作预测动力学建模目前已经成为了研究热点, 并进行了广泛而深刻的探索, 但是由于大脑工作机理的复杂性及其与神经疾病病态功能网络的紧密关联性, 对癫痫神经疾病的解剖结构、功能原理及其预测和调控, 特别是其动力学机理的理解, 仍然缺乏充分的实验和理论证据. 再加上癫痫电生理实验和临床表征的多样性和特异性, 为癫痫发作特征提取和统计建模提出了极大的挑战, 因此需要发展更加先进的多模态数据采集和数据融合分析方法, 并需要理论创新来进行合理的动力学建模分析. 为应对这些困境和挑战, 对癫痫发作预测动力学及其调控研究还应在以下方面进行更加深刻广泛的探索研究以期取得突破.

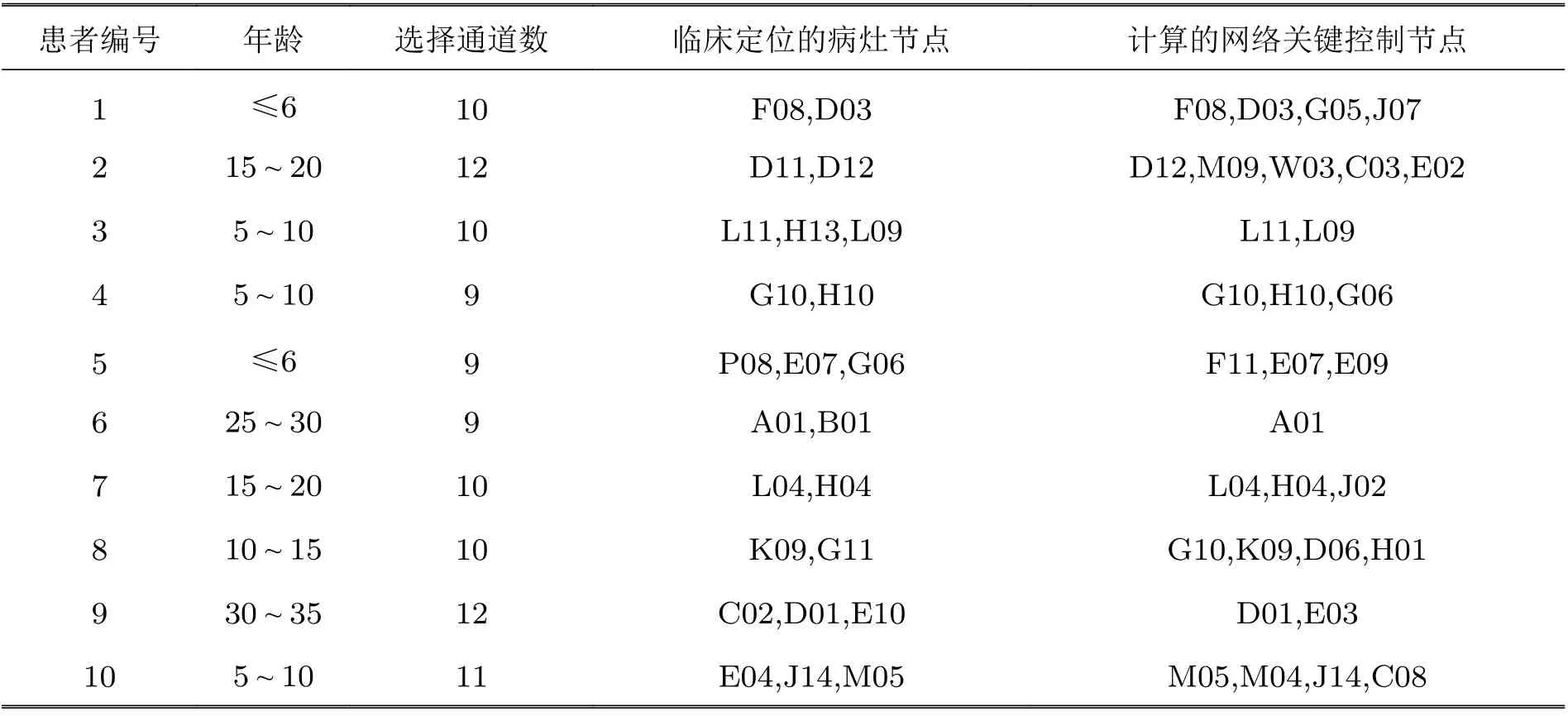
表 1 基于10 位局灶性癫痫患者计算的网络关键控制节点与临床定位的病灶节点对比

(1) 数据驱动的动力学理论建模及其参数优化

由于癫痫的复杂特性, 首先需要进行多模态数据采集和分析, 同时进行多模态数据的融合分析和相干性研究. 癫痫的动力学建模属于机理建模, 通过假定机理进行动力学建模, 并利用癫痫数据的分析来进行参数估计. 癫痫数据建模与机制建模结合, 将为癫痫发作行为的本质分析提供良好途径, 但如何建模同时进行模型参数优化并与临床发作特征相吻合, 是提高癫痫发作预测效果可靠性和设计有效调控策略的前提, 需要理论和方法上的突破, 可以成为今后的一个重点研究方向.

(2) 癫痫发作的时空涌现动力学机制研究

癫痫是脑神经网络系统的局部神经元集群突发异常同步振荡导致的慢性神经系统疾病, 具有复杂的非线性特征. 因此癫痫的发作具有复杂网络特性, 而涌现属性是复杂网络的重要特征之一. 实际上, 大脑通常以有序方式产生微电脉冲, 但在癫痫等神经疾病发作时脑电节律会失衡, 正常电模式被突然和同步的电能爆发所破坏, 具有显著的涌现行为特征. 但如何建模和分析癫痫的涌现动力学模型, 需要理论和方法上的创新, 也因此可以成为探究癫痫发生发展的时空动态演化的动力学机理的重要途径之一.

(3) 基于皮质-基底节-丘脑环路和海马环路的时空靶点优化选择

深脑刺激治疗不同难治性癫痫的最佳靶点和最优参数仍需进一步探索和确认, 以及刺激阻滞癫痫发展的机制仍缺乏合理解释. 特别是癫痫发作阶段的病态信息演化特性在不同研究对象之间存在很大差异, 目前尚未有通用方法来实现对所有癫痫患者的高性能发作预测和神经调控,所以癫痫发作机理和控制策略研究仍然是具有挑战性的基本科学问题和前沿交叉科学问题. 基于皮质-基底节-丘脑环路和海马环路的涌现机理, 发展临床多位点靶点动态识别与刺激模式自主调节的神经预见调控解决方案, 可以成为一个新的研究思路和框架.

致 谢 国家自然科学基金资助 (11932003, 12072021, 12102014, 11972115).