固液界面的力−电−化学耦合及在电催化体系中的应用

邓齐波 贾涵杏 杨 波 齐正磐 张哲绎 阿拉木斯 胡 宁 ,2,†

1 河北工业大学机械工程学院, 国家技术创新方法与实施工具工程技术研究中心, 天津 300401 2 河北工业大学电工装备可靠性与智能化国家重点实验室, 天津 300130

1 引 言

电催化剂在锂空气电池、燃料电池等新能源领域中扮演着至关重要的角色, 如何设计和制备高活性的电催化剂是产业界开发新能源面临的关键问题之一, 也是目前国际上学术界十分关注的研究领域.例如, 电化学析氧反应(oxygen evolution reaction, OER)是复杂的四电子转移过程, 其反应动力学十分缓慢, 严重制约着实际应用. 其中, 电催化剂是实现OER 高效反应的关键,性能优异的OER 电催化剂可以降低过高的反应能量, 加速反应动力学, 实现电能向化学能的高效转换.目前加速电化学反应的电催化剂有两类: 一种是贵金属基电催化剂(如二氧化钌、二氧化铱), 具有优异的OER 催化活性, 但较少储量和高昂成本阻碍了其大规模应用; 另一类是资源丰富的廉价过渡金属基电催化剂(如镍、铁)成本较低, 但催化活性不理想.目前国内外研究主要集中在对廉价金属电催化剂的改性上, 最直接的方法是从材料角度制备不同类型的电催化剂来提高其本征活性, 例如单原子、晶面控制、组分调控以及纳米结构化等(Han et al. 2016,Eftekhari 2017, Seh et al. 2017, 范玮等2018, Li et al. 2021). 最近的研究表明掺杂等材料改性手段也可以提升其本体的催化性能(张世龙等2019). 基于材料制备技术, 各式各样的新材料层出不穷, 然而其制备工艺过于复杂, 合成手段对环境不友好, 合成过程往往使用昂贵或危险的化学药品, 限制其实际工程应用, 因此亟需一种工艺简单、环境友好的提升廉价金属电催化活性的新策略.

近年来, 力学与电化学的耦合作用已快速发展成为一个新能源材料中的新兴领域(Zhao &Cui 2016, Liang et al. 2019, Li et al. 2019, Zhu et al. 2019). 一方面, 电极材料在电化学过程中产生较大的应力, 从而导致材料的力学破坏, 继而影响其电化学性能(马增胜等2013, Tavassol et al.2016, Xu & Zhao 2018). 针对锂电池电极材料的力化学耦合断裂行为, 我国力学领域的科研工作者已开展了一系列较深入的原创性工作, 在学术上做出了重要的贡献(Ma et al. 2017, Xie et al.2017, 杨盼盼等2018, Burebi et al. 2019, Wang P et al. 2019, Liu et al. 2019). 通过建立力学-电化学耦合理论模型来理解和探究力学诱导锂电池电极失效机制, 进而指导科研人员更好地设计材料来提升电化学性能, 实现复合材料在柔性电化学储能装置中的应用(朱博等2020, 张豪等2020). 另一方面, 除了二次电池等储能电池以外, 以电催化反应为基本原理的燃料电池也是目前新能源领域的研究热点之一. 由于其整个电催化过程都是在电极材料表面上进行, 材料的表面效应对电催化反应尤其关键. 许多新型结构金属催化剂都能看到表面力学的身影, 例如多金属构成的层状结构、核壳结构, 催化剂表面高活性原子受到来自于基底不同程度的应力/应变作用.微观上是催化剂表面的高活性原子间的晶格常数发生了改变, 此变化反映了晶体内部受力状态的变化情况, 宏观上则是材料表面发生了形变.最近的一系列研究发现这种表面应变效应对新型金属催化剂的电化学性能产生了显著影响(Khorshidi et al. 2018, Wang L et al. 2019a, Yao et al.2020). 应变能够直接改变金属的能带带隙, 进而有效提升金属材料催化活性, 为高活性电催化剂的开发提供了一个新的思路.

本文将针对电催化性能提升的应变效应, 在归纳总结最新研究进展的基础上, 系统阐述催化剂在电化学反应过程中力化学耦合行为的相关理论描述和主要应用研究进展. 第2 节介绍电催化体系中力化学耦合的理论研究; 第3 节介绍电催化体系中力化学耦合的基本实验手段; 第4 节介绍基于交变载荷的力学方案研究应变调控电化学过程的相关工作; 最后展望表面力学在电催化体系中应用的研究重点和发展趋势.

2 电催化体系中力化学耦合的理论研究

目前电催化体系中力化学耦合领域的理论研究主要包括两个方面: (1)基于热力学和连续介质力学框架的理论分析; (2)以第一性原理为主的计算分析.

2.1 基本理论: 固液界面的热力学表述及麦克斯韦关系式

20 世纪70 年代, Gurtin 和 Murdoch (1975)从固体力学的角度分析了一般非均匀曲面应力和应变的数学表达. 随后国内外开展了一系列表界面力学相关研究，在理论和计算模拟方面取得了丰硕的学术成果。 赵亚溥(2012)及其“纳微系统与物理力学”课题组一直在微纳尺度表面与界面力学领域开展多年的研究工作, 其撰写的《表面与界面物理力学》从连续统角度出发, 以分子间作用力为关键点, 综合讨论了固-液、固-固、固-气以及固体与生物等界面物理力学行为.该著作(赵亚溥 2012)详细介绍了表面与界面问题的热力学框架和统计理论、联系固体宏微观变形的Cauchy-Born 准则与近平衡态输运特征的Green-Kubo 公式等理论基础知识; 针对不同类型固-液界面的接触线移动问题, 给出了具体问题的由来, 详细描述了移动接触线问题中的跨尺度特征以及固-液界面相互作用, 并重点讨论了多物理化学场耦合对表面张力的影响; 该著作还针对分子马达和微悬臂梁传感器, 提炼了经典的界面力学问题和相应的模型, 最后系统介绍了表面与界面扩散与演变动力学、相场动力学方法在润湿与电润湿等表面与界面物理力学中的应用. 随后, 赵亚溥(2014)在另一本著作中针对固-固界面之间的黏附力学问题, 系统介绍纳米和介观力学的理论框架和基础, 并围绕微纳系统(MEMS/NEMS)的接触力学、界面剥离力学以及黏附接触滞后等问题进行了细致的讨论、归纳和总结. 这些经典著作在国内首次从表面和界面的微观物理、物理化学出发, 结合纳米与介观力学角度, 阐明了表面和界面的物理力学机理, 揭示了力-电-化耦合效应对于固液界面的重要影响, 对深入研究电催化过程具有重要意义.

上述研究成果从不同角度详细地阐述了材料表面与界面多物理化学场耦合作用对材料表面特征的影响机理, 例如表面应力的变化. 鉴于整个电催化过程都是在电极材料表面上进行, 材料的表面效应对电催化反应尤其关键, 那么表面应力、应变的变化能否影响电极材料表面的电化学性能 (催化性能等)? 针对这一问题, Weissmüller 和 Kramer (2005) 考虑了电化学体系的液态电解质和金属电极, 并基于连续介质力学框架理论分析了在材料表面产生变形的情况下电化学体系的热力学平衡态问题, 并在此基础上开展了许多深入的理论和实验研究.因此, 本小节主要基于Weissmüller 和 Kramer (2005)的相关理论介绍外应变作用下的电催化体系中力-电-化学耦合关系.

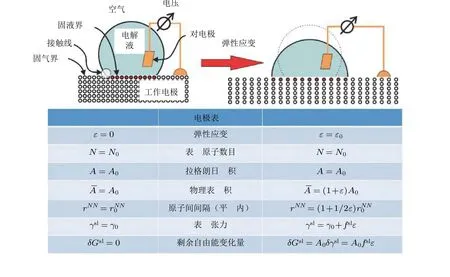
图1在电极电势保持恒定时, 对电极施加弹性应变(ε)作用(图1 右侧), 金属材料面内原子间距从增大到 , 进而增大电极物理表面积(). 另外,拉格朗日面积A 和表面原子数目N保持不变. 系统吉布斯自由能的变化量与表面应力 (f sl) 成比例, 即 Gsl =A0fslε (Weissmüller 2013)

将固体金属电极与液态电解质的接触界面(图1 左)作为研究体系, 整个系统的净自由能包括固体、液体以及固液界面三个部分. 吉布斯自由能(也称为剩余自由能),Gsl=γslA, 与固液接触界面的电极表面拉格朗日面积A和表面张力γsl密切相关. 在电化学过程中保持电极电势E不变的情况下, 沿着电极表面切向方向施加大小为ε0的弹性应变ε(如图1 右图所示), 物理表面积将随弹性应变的施加而发生变化, 而由于表面原子与固液接触线一起发生相同的位移, 在拉格朗日框架内接触线保持静止, 因此电极表面原子数以及拉格朗日面积将保持不变. 这意味着在拉格朗日框架下吉布斯自由能的变化Gsl将 完全由表面张力的改变所引起, 即δGsl=A0δrsl.

弹性应变的施加改变了电极表面金属原子的间距, 进而改变了金属表面状态, 导致表面张力的变化. 由于表面应力fsl可以表述为固体表面张力关于弹性应变的一阶偏导数, 即fsl=∂rsl/∂ε(Cahn 1978), 系统吉布斯自由能的变化量可以表示为

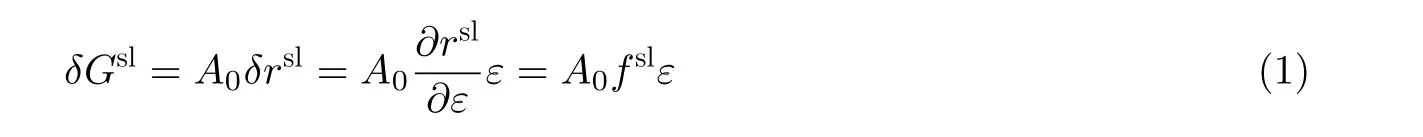
从式(1)可得知在弹性应变作用下, 与系统吉布斯自由能变化量直接关联的变量不是表面张力, 而是它的一阶应变导数, 即表面应力. 金属电极电化学过程中力学平衡受表面应力的控制, 而自由能的变化量也严重依赖于应变变量.

Weissmüller 和 Kramer (2005)在考虑固液界面系统中对电极表面施加切向弹性应变时, 采用表面自由能密度函数ψ来描述表面剩余能量(surface excess in energy), 电极表面自由能密度来源于弹性应变和电解质两个部分. 电解质在电极表面的吸附量Γ与电荷密度q相关联, 即dq=Σ-zFdΓ(其中F为法拉第常数,z为电解质中离子的价态). 因此, 表面自由能密度ψ可表述为以切向应变ε和表面电荷密度q作为自变量的状态函数, 即ψ=ψ(q,ε). 通过勒让德变换(Legendre transform)得到状态函数ψ与表面张力r的关系式:r(ε,E) =ψ(ε,q) -qE(详见Weissmüller &Kramer 2005, Kramer & Weissmüller 2007). 从能量的角度考虑, 与应变ε和电荷密度q相关的能量共轭变量分别为表面应力f和电极电势E, 在外部压强等参数恒定的条件下表面自由能密度函数ψ的微分形式可以表示为

由表面自由能密度的二阶导数可得到

式(3)被称为电化学体系的麦克斯韦关系式, 该关系式联系了毛细力、状态变量和电化学体系中的电荷/电势. 关系式(3)的左侧dE/dε|q=ςE被定义为电毛细管耦合系数(electrocapillary coupling coefficient), 也称为电势-应变响应系数(potential-strain response coefficient), 即电极电势关于表面应变的导数, 对于不同材料ςE是已知的或可测量的. 关系式(3)的右侧df/dq|ε=ςf称为应力-电荷响应系数(stress-charge response coefficient), 即表面应力关于电荷密度的导数. 当系统处于平衡状态时, 在恒定电荷密度下电极电势对于弹性应变的响应(ςE)与恒应变下表面应力对于表面电荷密度变化的响应(ςf)数值相等, 即ςE=ςf.根据方程的右侧可以得知由电极电势变化所引起的表面电荷密度的变化, 导致了表面应力的变化; 这也解释了充放电过程中金属电极表面应力变化的现象(Smetanin et al. 2008, Lafouresse et al. 2012, Han et al. 2016, Wang H et al.2017). 根据关系式(3)左侧(dE/dε|q)可知, 当表面电荷密度q为恒定时, 如果在金属电极表面作用往复变化的机械应力或者应变, 电极电势将会产生往复变化的现象, 这是一个机械能转化为电势能的过程, 因此理论上验证了表面力学行为导致材料表面形变, 进而改变电极电势, 影响电极电化学反应的进程.

对于一个电化学离子吸附过程, 离子在电极表面吸附焓的变化量(Δhad)与吸附电势(ΔEad)的关系为

式中F为法拉第常数,z为电解质中离子的价态.由于在电化学离子吸附过程, 系统的电荷基本保持平衡, 应变可导致电解质中的离子在金属电极表面吸附焓的变化

式中ςad为吸附电势(Ead)下的电势-应变响应系数. 系数ς描述了电化学过程电势随外应变的变化规律, 而电势与电化学反应过程离子在电极表面的吸附能密切相关, 因此在实验中通过测定ς值来定量表征应变对电化学过程的影响.

上述热力学推导过程假设整个固液界面体系的热量恒定不变, 忽略了电催化过程所产生的热量. 值得注意的是，热管理以及热分析在电催化过程中十分重要, 尤其在以电催化反应为原理的燃料电池.例如质子交换膜燃料电池(PEMFC)工作过程中所产生的热量在一定程度上可以提高电催化剂的活性, 提高电池内化学反应速率, 对冷启动也有利, 但是电催化反应过程伴随的过高温度会导致膜皱缩甚至破裂, 造成膜两侧气体相互掺混, 进而导致燃料电池的安全事故. PEMFC 属于低温燃料电池, 仅仅依靠与空气自然对流和辐射换热的散热形式是非常有限的, 因此需要通过科学的热管理控制产热与散热的平衡, 实现热量的均匀分布, 让整个电池的实际温度处于最优设计点温度的附近.目前在PEMFC 的热管理研究中, 大部分采用的是数值仿真与实验相结合的方法, 一般先用FLUENT, ANSYS, MATLAB 或COMSOL 等仿真软件建模, 然后用实验数据验证模型的正确性, 从而使模型可用于指导PEMFC 的设计与优化(侯健等2021).

关于界面热问题的理论分析, Murdoch (1976)建立了三维连续体之间界面的热力学理论, 基于线性旋转动量和能量的平衡方程, 以及三个温度场变量的熵增不等式(entropy-growth inequality), 通过考虑界面的热-力相互作用, 研究了界面应力和自由能之间的关系, 获得外部传热的各种本构关系所对应的不同热传导不等式. Wang 和 Zhao (2011)在连续介质热力学的框架下提出了纳米结构材料表面和大体积的热超弹性模型, 考虑了残余应力的作用.由于残余应力的存在,即使在无穷小变形的情况下, 表面(或体积)热超弹性本构方程的不同构型描述是不相同的,Wang & Zhao (2011)采用热超弹性模型分析了球形纳米粒子的等效热膨胀系数.根据Wang 和Zhao (2011)的热超弹性模型可知: 在没有外部机械或热负载的情况下, 表面残余应力会在大量的纳米结构材料中引起一个应力场, 这种额外的应力场将影响材料表面的电催化过程.因此, 关于固液界面力-电-化学耦合的热力学表述需要进一步考虑电催化过程热量的影响. 然而目前针对电催化过程中热量的理论分析较少, 本文将主要关注不考虑热量影响的固液界面力-电-化学耦合及在电催化体系中的应用.

2.2 第一性原理计算

基于密度泛函理论(DFT)的第一性原理计算在建模中通过金属面内晶格参数的改变来表示切向方向的应变状态. DFT 计算表明当晶格参数发生变化时非均相催化中的反应速率会发生明显变化(Mavrikakis et al. 2000). 基于计算结果晶格应变能够改变金属催化剂的电子结构, 导致反应物在其表面的吸附焓以及反应过渡态能量的改变, 从理论上预测应变能够影响电催化反应的速率. 目前用于解释应变对电子结构的影响主要基于Hammer 和 Nørskov (1995)所提出的d 带中心的理论模型. 在该模型中, 应变对金属表面反应活性的影响归因于金属d 带中心的偏移. 根据d 带模型, d 带中心的位置对吸附能和反应活化能垒起决定作用. Mavrikakis (1998) 通过比较应变状态下以及没有应变作用的金属Ru (0001)表面的吸附和解离性能, 得出如下的规律: 拉伸晶格应变使金属的d 带中心发生上移, 从而与吸附物质发生更强的相互作用, 而压缩应变使d 带中心发生下移, 从而减弱相互作用. 迄今为止, 这个d 带模型已成为表面应变与催化活性之间的根本关联, 与前文提到的吸附焓与应变相关性的数学模型相一致. 以金(Au)为例, 美国Mavrikakis 等（2000）根据DFT 的计算结果发现: Au 表面原子的晶格增加了1%, 导致一氧化碳气体(CO)在原本惰性Au 表面的结合能提高了0.05 eV, 从而改变了Au 对CO 电氧化的催化性能. 对于电化学析氧反应(OER), DFT 结果表明拉应变导致Ni 和Fe 原子的d 带中心向上移动, 增强反应中间体的结合, 从而预测拉应变可以增强材料的OER 活性(Wang A Q et al. 2019).

以上的变化趋势一般只适用于后过渡金属(late transition metals, 即d 带填充超过一半), 包括了大多数催化材料的组成元素. Schnur 和 Groß (2010)的研究发现: 与典型的后过渡金属相比,前过渡金属(early transition metals)由于其d 带填充小于一半, 具有更低的晶格膨胀吸附能.这种不一致性可以在经典d 带模型的基础上给以合理的解释: 表面拉伸应变可以减少波函数的重叠,从而缩小金属的d 带带宽; 而对于前过渡金属, 由于带宽变窄, d 带的数量增加, 使得d 带中心发生下移, 进而保持d 带的填充程度(图2(a)), 从而减少金属表面原子与吸附物的相互作用; 而对于后过渡金属, 为保持d 带的填充程度, 在相同机制作用下其d 带中心将发生上移(图2(b)), 从而增强了金属与离子吸附之间的相互作用.因此, 前过渡金属与后过渡金属在吸附能与应变的相关性方面刚好相反(Schnur & Groß 2010).在理论计算方面, 目前的研究往往在不同晶格应变的作用下, 基于DFT 计算分析反应物以及反应中间体在不同种类催化剂表面上的吸附能相对变化量来描述晶格应变对材料电化学催化活性的作用.

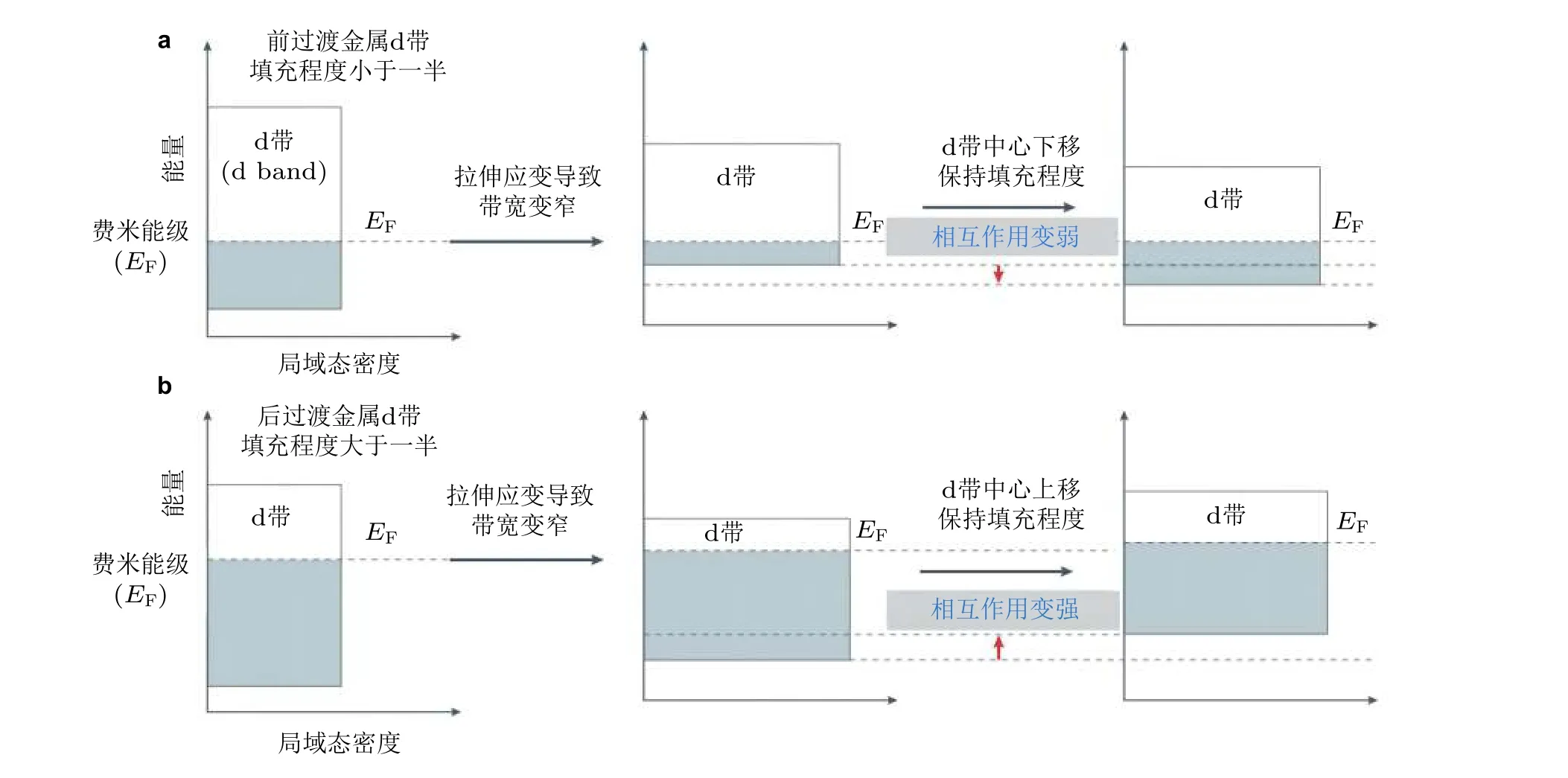
图2 d 带模型理论: 对于前过渡金属(a)和后过渡金属(b)拉伸应变对其d 带位置的影响. 拉伸应变都会使前过渡和后过渡金属的d 带宽度变窄, 为了保持d 带填充程度(即电荷守恒), 前过渡金属d带中心将下移, 而后过渡金属d 带中心上移 (Luo & Guo 2017)

Maark 和 Peterson (2014)基于密度泛函计算研究了不同金属基底(Ru, Ir, Pt, Au)表面的单原子层Pd(111)的电化学析氢反应催化活性. 由于活性层原子除了受到晶格应变作用外, 还会受到来自于活性层原子与基底之间电子结构的耦合作用(ligand effect, 也称为配位效应), DFT 计算结果表明应变效应和配位效应都能影响氢在Pd 表面的吸附自由能. 基于DFT 理论计算的方法Maark 和 Peterson (2014)具体计量化了这两种效应对氢吸附自由能贡献的相对大小(如图3).

Guo 等 (2014)以Ag 或Au 为核, CuPd 合金为壳, 通过调节催化剂的组成成分和壳层厚度,得到了一系列Pd 基核壳结构的纳米催化剂, 并基于DFT 计算分析氧在其表面的相对结合能(ΔEO), 如图4 所示. 理论计算结果表明ΔEO随着合金晶格压缩呈单调增大, 这是由于Cu 的晶格常数小于Pd, 合金中铜含量的增多会导致更大的压缩应变, 进而使ΔEO值增大. 然而, 壳层合金中较大的铜浓度(图4(c)中的绿色曲线)实际上降低了ΔEO值, 这与氧在铜表面结合过强的现象是一致的. 因此, 随着壳层铜含量增多, 其应变效应与化学效应之间存在着竞争关系.

3 电催化体系中力化学耦合的基本实验手段

Gsell 等 (1998)通过扫描隧道显微镜技术实验研究了不同表面局部应变对氧吸附能的影响.通过气泡的内嵌来实现材料表面不同的局部应变状态. 实验结果表明, 与没有应变作用的表面相比, 氧原子优先吸附在Ru(0001)表面处于横向膨胀的区域, 而在横向晶格收缩区域则较弱, 证实了应变可以影响吸附物在材料表面的吸附强度.该研究中, 作者指出了由于实验证据并不是很充分, 因此需要更为深入的理论和实验方面研究来进一步理解这些应变效应.随后国内外学者及研究机构在应变影响电催化活性方面进行了广泛的实验研究, 并取得了众多创新性的研究成果. 以下将归纳总结近年来关于电催化活性应变效应的实验研究方法.

3.1 材料制备手段

关于应变影响材料电催化性能的实验研究, 目前最常用的手段是直接的材料制备方法.科研人员通过电催化活性物质层与基底材料晶格不匹配来产生表层应变(即晶格失配应变), 进而研究该晶格应变对材料电催化活性的影响.

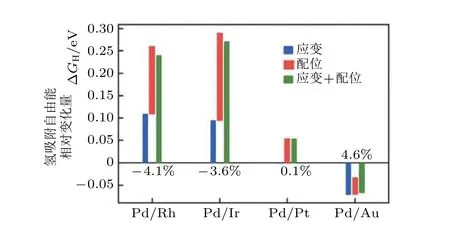
图3应变效应和配位效应对氢在Pd 表面吸附自由能的影响 (Maark & Peterson 2014)

例如, 通过单原子层的金属钯(monolayer Pd)外延生长(epitaxy)在不同金属基底上, 得到双金属的层状结构(PdML/基底)(Kibler et al. 2005), 如图5(a)所示. 通过测量不同双相金属结构表层Pd 原子间距发现表层Pd 原子间距发生了变化(图5(b)), 随后通过电化学手段研究不同基底上的单原子层Pd 的电化学析氢反应(HER)性能, 主要体现在图5(c))的吸附电势(横坐标, adsorption potential,EHupd)和反应交换电流密度(纵坐标, exchange current density,j0), 在实验上证实了晶格应变能够影响Pd 表面电化学析氢反应.

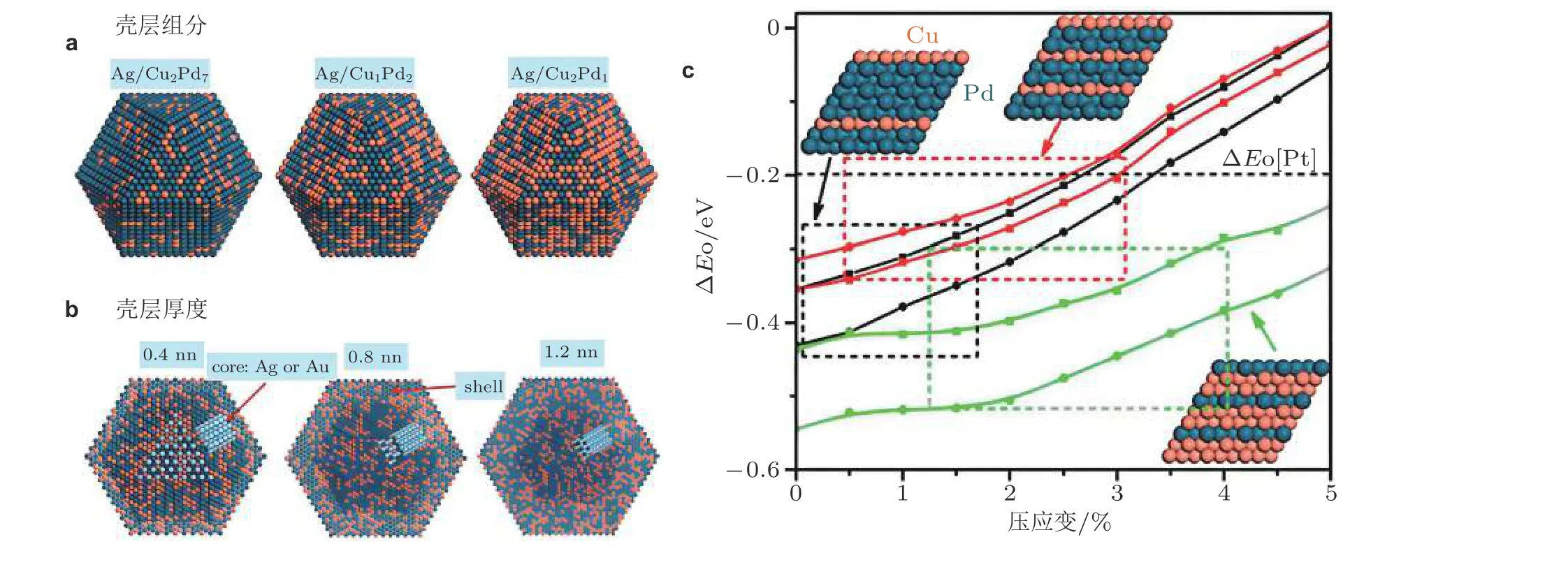
图4以不同铜钯组分(a)和厚度(b)为壳层, 银(或金)为核体的核壳结构材料, 氧相对结合能(ΔEO)随应变的变化关系(c). 黑色、红色和绿色的曲线分别代表壳层组分Cu∶Pd 的原子比值为2∶7、1∶2 和2∶1. 相同颜色的不同曲线对应于氧在不同的面中心立方空心吸附. Pt(111)表面上的ΔEO 用水平虚线表示 (Guo et al. 2014)

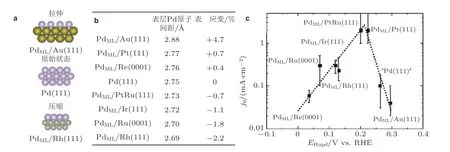
图5(a)金属钯Pd(111)以及外延生长在不同基底上的钯单原子层(PdML)晶格关系图, (b)不同双相层状结构表层Pd 原子间隔(1 Å = 0.1 nm), (c) Pd(111)以及PdML 的析氢反应性能 (Kibler et al.2005, Kibler 2008)

外延生长的材料方法一般通过催化活性层的厚度来调控其表面应变的大小. 例如表面应变随着电催化活性层Pd 膜厚度的变化可以很好地解释同一材料成分表面不同的吸附行为和反应活性, 而随着厚度的增加材料电催化性能也更趋于块体材料(Kibler 2008). 应变不仅可以影响单质金属表面活性, 还可以影响金属氧化物的电催化性能. Li 等 (2016)通过毛细力的作用将含有氧空位的二硫化钼(MoS2)薄膜附在凸起的金纳米锥表面, 使MoS2在金纳米锥顶端位置受到拉伸应变, 在氧空位与应变共同作用下氢在MoS2表面的吸附自由能发生改变, 进而提升电化学析氢反应的催化活性.

除了外延生长的方式制备层状结构外, 还可以引入其他物质形成核壳结构来产生晶格失配,进而通过晶格应变来提升催化材料的反应活性.电化学氧还原反应(oxygen reduction reaction,ORR)在电化学过程中是一类非常重要的反应, 同时也是燃料电池正极电极所发生的过程, 由于其反应动力学非常慢, 促进其反应过程也一直以来是新能源领域研究的一个重要方向. 研究人员在现有基础上利用晶格应变的策略来进一步提升电催化材料的性能. 德国柏林工业大学Strasser等(2010)对表面覆盖有铂(Pt)原子层的Pt-Cu@Pt 核壳结构催化剂进行了氧还原反应研究: 通过X-射线衍射法等测试手段从原子尺度研究了催化剂的表层壳体结构, 他们发现核体中Cu 含量的改变导致了Pt 壳层晶格的变化, 并分析不同表层壳体结构的Pt 晶格变化与催化活性的关联性, 表明表面应变是影响催化剂ORR 催化活性的关键因素.

在Strasser 等 (2010)工作基础上, Seh 等 (2017)系统地研究了8 种Pt-镧系的核壳结构材料Pt5M, 其中M 为镧( La )、铈( Ce )、钐( Sm )、钆( Gd )、铽( Tb )、镝( Dy )、碲( Tm )以及钙( Ca ). 该研究利用镧系元素晶格的收缩来控制表面壳体Pt 的应变大小(图6), 进而调节这些材料在部分脱合金后的稳定性和反应活性. 基于应变与反应活性关联性的计算结果表明, 压缩应变约3%的电催化剂Pt5Tb 表现出最强的反应活性.

Wang 等 (2015)基于钯二十面体制备了Pd/Pt 核壳结构, 由于双晶边界的侧向约束和垂直弛缓作用, 铂层产生的压缩应变大幅度提升了其在氧还原反应的催化活性. 在此基础上Bu等 (2016)制备了PtPb/Pt 核壳结构的纳米催化剂, 并结合实验与DFT 计算研究了应变在ORR催化反应中的作用, 研究发现该催化剂Pt 壳的厚度约为1 nm (等于四个原子层)时, 最外层的Pt(110)面上具有较大的双轴应变, 压缩应变减弱了其与含氧反应中间体的结合, 增加了Pt 的氧还原催化活性. DFT 计算表明Pt(110)面合适的应变大小有助于将Pt-O 键强度降低到优化值.在应变作用下, 这种纳米结构在实验中表现出优异的ORR 催化面积活性(7.8 mA/cm2)和质量活性(4.3 A/mg). 苏黎世联邦理工学院Temmel 等 (2016)同样采用晶格应变的策略发现Pt 原子受到0.3%的晶格应变时其ORR 催化活性提高了8 倍. 美国斯坦福大学Wang 等 (2016)利用常见的锂离子电池电极材料(LiCoO2)作为支撑, 在铂纳米颗粒表面实现了压缩应变到拉伸应变的可调节设计, 如图7 所示.该研究中锂电池正极钴酸锂颗粒在电化学充放电过程中所产生的膨胀或收缩对颗粒表面沉积的Pt 活性层产生应变作用, 结果表明压缩应变可以提高Pt 的ORR 催化活性.

对于电化学析氧反应(oxygen evolution reaction, OER), 美国太平洋西北国家实验室Stoerzinger 和新加坡南洋理工大学Wang 等(2019b)的合作研究发现: 基于材料制备手段所产生的晶格应变和氧空位可以提升NdNiO3薄膜材料的OER 活性. 中国科学技术大学Cheng 等 (2019)将晶格应变引入到过渡金属镍铁基金属有机框架(NiFe-MOF)材料中, 获得了出色的析氧反应和氧还原性能. 在材料领域往往会采用掺杂的方式来提升OER 催化剂的活性, 最近的研究表明这种掺杂方式同样也存在应变效应. 德国波鸿大学Masa 等 (2019)的研究表明所掺杂的原子(硼、磷)对主体原子(镍)产生明显相反的电子效应, 但这两种元素反而都会促进镍的析氧电催化过程, 掺杂磷后相邻Ni 原子之间的间距为2.640 Å, 而掺杂硼后Ni 原子最短的间距为2.530 Å, 均大于纯Ni 材料的原子间距(2.492 Å).文章指出硼或磷的存在引起的镍晶格结构的变化是硼化镍和磷化镍中OER 电催化活性增强的主导因素, 而不能简单通过电子结构的改变来理解OER 活性增强的根源.

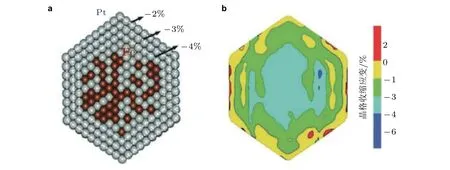
图6(a)以Pt50Fe50 合 金 为 核Pt 为 壳 的 结 构 模 型, 压 应 变 梯 度 从−4% ～ −2% (相 对Pt 体 相 材 料);(b)晶格收缩应变图(Seh et al. 2017)

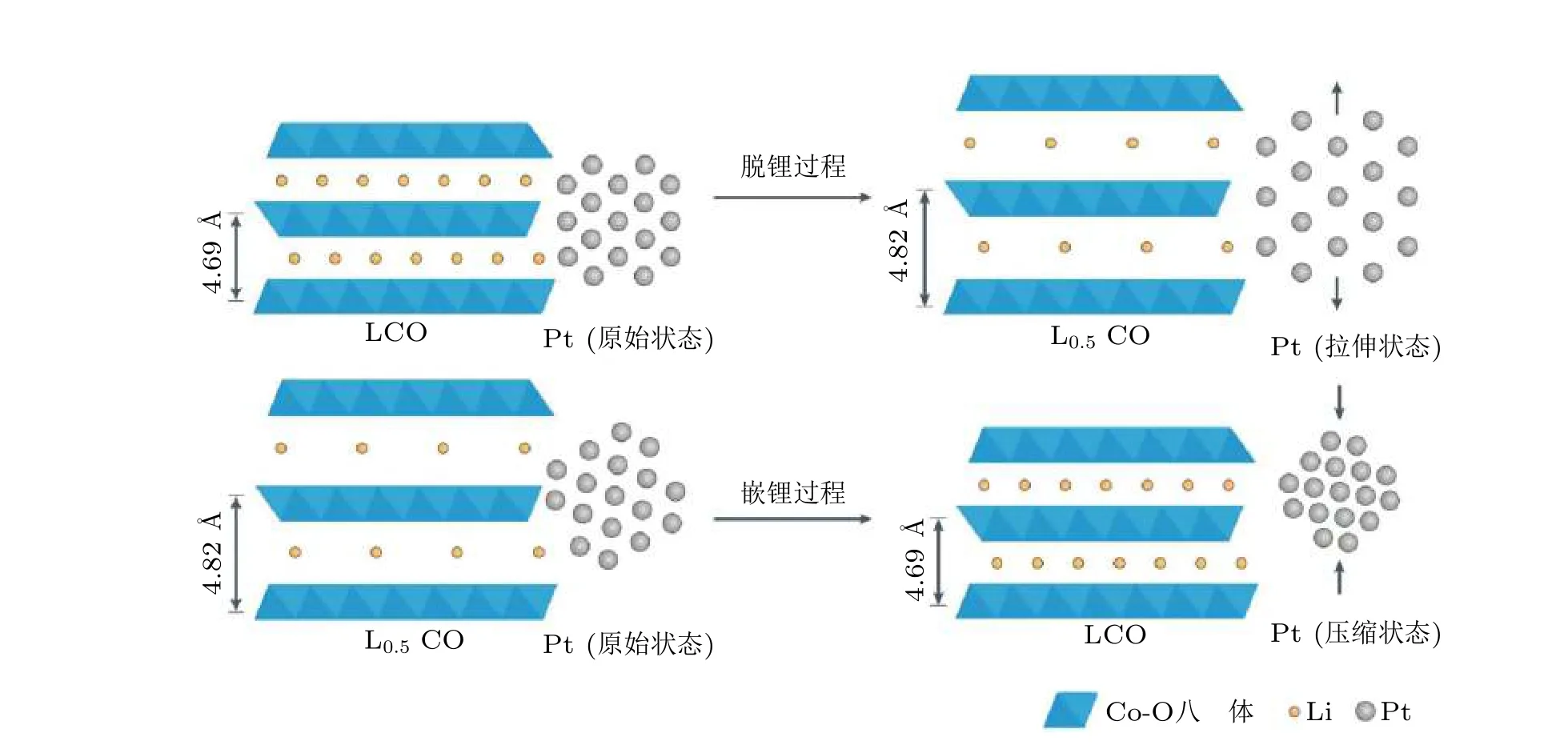
图7基于锂离子电池电极材料LiCoO2(LCO)的充放电来改变催化活性物质Pt 纳米颗粒的晶格应变(Wang et al. 2016)

除了上面提到的电化学析氢反应、电化学析氧反应以及电化学氧还原反应, 目前基于晶格畸变的材料制备手段也应用在其他重要的化学体系中, 例如二氧化碳电催化还原(Huang et al.2017)、传统费-托合成反应(Xue et al. 2018).

这些研究成果表明应变可以较大幅度地改善金属基材料电化学反应的催化活性.然而目前基于晶格不匹配所产生的应变通常与空位、缺陷或配位效应(基底效应)等因素共存, 造成应变-活性相关性的识别十分复杂, 不能有效地归纳总结应变对反应催化活性的影响规律和揭示其物理机理.例如, 分别将图5 中的反应交换电流密度和氢吸附电势的实验数据作为纵坐标, 晶格应变值作为横坐标, 如图8 所示, 明显地看出用来描述电化学析氢反应性能的反应交换电流密度以及氢吸附电势随晶格应变值大小变化的趋势是杂乱无章的.

在大部分研究应变与电催化活性关联性的实验中, 通常由两种及以上金属材料(表面活性层与基底)的晶格不匹配来产生静态应变. 前文提到基于晶格畸变的活性层原子除了受到晶格应变作用外, 还会受到来自于活性层原子与基底之间电子结构的耦合作用(配位效应), 这种配位效应同时影响材料的电催化活性(Kitchin et al. 2004, Gauthier et al. 2001, Schlapka et al. 2003, Maark& Peterson 2014). 例如, Schlapka 等 (2003)采用实验和理论相结合的方法研究了应变效应以及配位效应对CO 吸附能的影响. 在Ru(0001)衬底上沉积Pt 单层的晶格压缩以及强的Pt-Ru 层间电子耦合的配位效应导致CO 吸附能的显著降低, 这两种效应都导致了金属的d 带中心下移. 一般来说, 在双相金属层状结构、核壳结构等新型金属电催化剂中, 金属间应变效应和配位效应同时存在且不容易分离. 此外, 表面的缺陷同样可以影响材料的电催化活性. 河北工业大学陈贵锋等(2018)的研究结果表明表面缺陷可以较大幅度促进SnO 微板在中性电解质中的电催化性能.

最近的一系列综述文章也指出了依靠常规材料制备手段的应变工程在电催化反应中存在的问题. 例如, 新加坡南洋理工大学You 等 (2019)在最近的《Advanced Materials》综述文章中详细介绍了晶格不匹配引起的应变工程在水分解反应的作用(析氢反应和析氧反应), 指出关于晶格应变策略的不足之处: “常规材料手段得到的晶格应变通常与空位和缺陷等其他因素共同产生, 这使得应变-活性相关性的识别复杂化, 仍然需要更为精确的应变生成策略.” 北京大学Luo和 Guo (2017)在《Nature Reviews Materials》关于应变与电催化反应关系的综述文章中同样也指出: “精确定量晶格畸变所诱导的应变值需要对纳米催化剂中原子的三维位置有很高的精度,这在目前使用的技术中不易实现” “目前可用的材料合成手段限制了对纳米催化剂表面应变的调控.”

3.2 形状记忆效应

除了晶格不匹配的材料制备手段外, Du 等(2015)根据预拉伸处理的形状记忆合金在温度变化时会发生相变收缩的原理, 实现了NiTi 表面沉积的Pt 薄膜催化剂不同拉压应变状态, 然后研究不同应变状态对Pt 薄膜ORR 催化性能的影响.形状记忆合金可逆相变伴随着样品几何尺寸的变化, 如图9(a)所示, NiTi 在加热过程中的第一次反向马氏体转变中收缩了7.5%, 然后在冷却过程中从200 ℃变化到-100 ℃的3.5%, 这3.5%的应变可以在接下来的加热过程中再次恢复.因此, NiTi 表现出3.5%的可逆双向记忆应变. 通过利用NiTi 的双向形状记忆效应, 沉积在该基底上的铂纳米膜可以具有较大的应变状态, 并影响Pt 薄膜的电化学性能(图9(b)). 在此基础上,Du 等 (2016)还研究了由形状记忆合金所产生的应变对半导体光催化活性的影响.

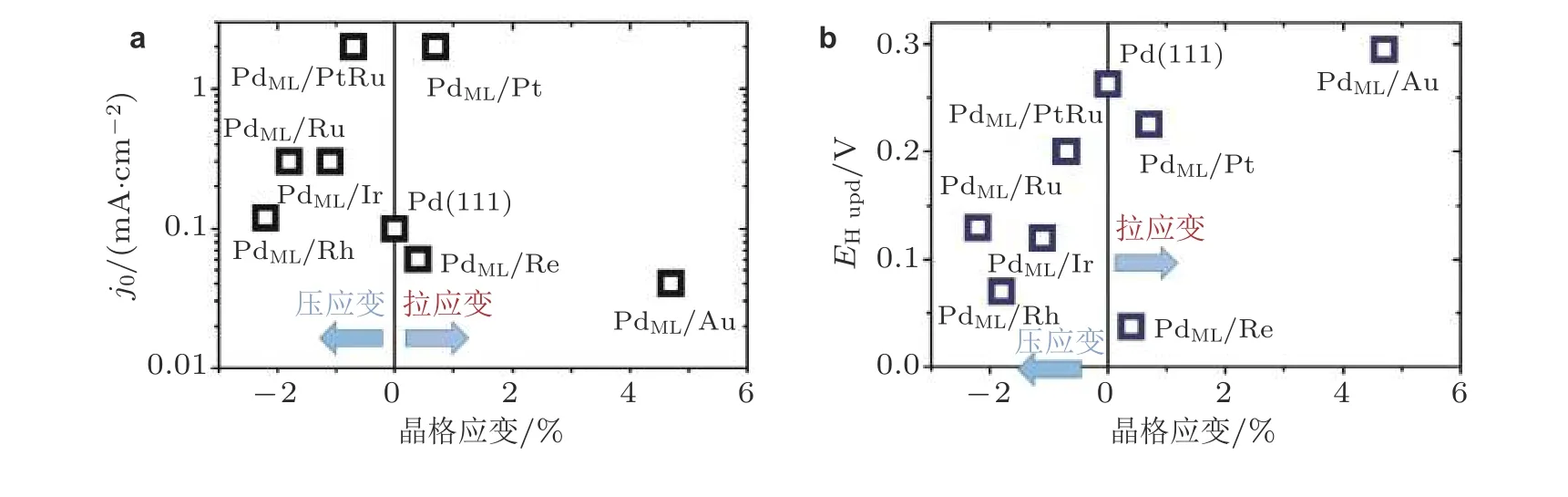
图8(a)析氢反应交换电流密度(j0)与晶格应变的关联性, (b)氢吸附电势(EH upd)与晶格应变的关联性 (图中数据来自于图5)

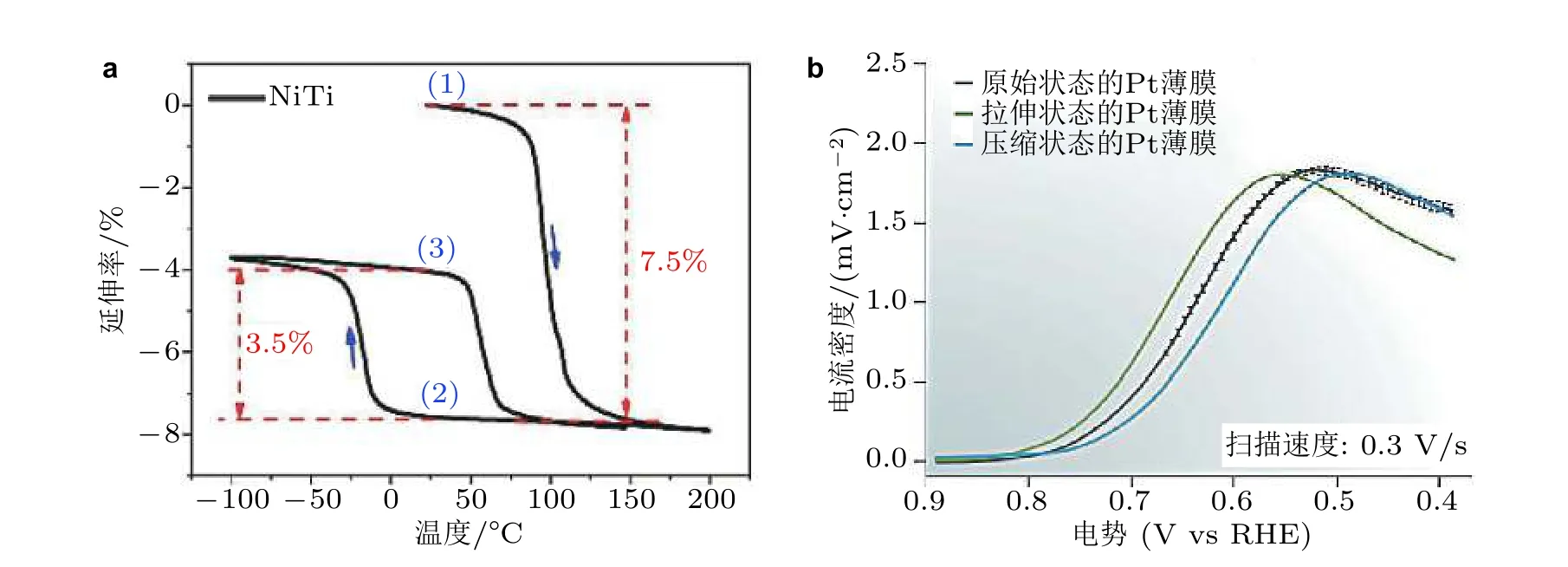
图9(a)预变形的NiTi 衬底的相变行为, (b)表面不同应变状态下Pt 薄膜的电化学性能 (Du et al. 2015)

Muralidharan 等 (2016)同样采用镍钛合金丝作为衬底, 在表面形成镍基金属氧化物. 在碱性溶液中测试了拉伸应变对镍基氧化物电化学性能的影响. 实验结果表明: 对镍基金属氧化物施加小于0.1%的应变, 阳极峰和阴极峰的电势向较低的方向发生移动(图10), 偏移量为-30 mV. 当镍基金属氧化物恢复到无应变状态时, 阳极峰和阴极峰电势移动至原始位置, 由此可知表面应变可以调节金属氧化物的电化学电势.

除了形状记忆合金外, Yuan 等 (2019)基于聚乳酸(PLA)基底热变形的特性, 在其表面磁控溅射制备金属薄膜样品, 通过加热冷却过程获得了不同受拉或受压的金属薄膜样品.金属层的静应变可以达到1%的量级, 通过循环伏安法研究发现金属薄膜应变可以影响电极表面氧的电吸附过程.

3.3 静载荷作用

在金属晶体内部成分不变的情况下, 晶格的畸变反映了晶体内部受力状态的变化, 在宏观角度上材料发生变形, 受到应力的作用. 因此, 通过施加外载荷的方式也是实现催化活性层应变的有效手段.

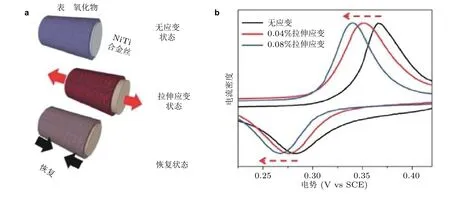
图10(a) NiTi 合金丝不同应变状态, (b)表面不同应变状态下镍基氧化物薄膜的电化学性能 (Muralidharan et al. 2016)

美国布朗大学Peterson 课题组Yan 等 (2016)在聚甲基丙烯酸甲酯(PMMA)衬底上采用物理溅射制备了Pt 薄膜, 通过机械方法对PMMA 衬底施加应变, 金属薄膜间接地受到拉伸或压缩应变, 进而研究了静载荷作用下应变对金属薄膜电极表面电化学析氢反应的影响(图11): 在Pt薄膜电极表面施加和卸载应变的过程中, 测试Pt 薄膜电极表面的循环伏安曲线, 压缩应变状态下的Pt 薄膜的循环伏安曲线向右移动, 电化学反应的过电势降低; 而拉伸应变状态下 Pt 薄膜的循环伏安曲线向左移动.这表明压缩应变增强了Pt 薄膜表面析氢反应的催化活性, 拉伸应变降低了Pt 的催化活性.随后该课题组还研究了静载荷作用下应变对碳化钨材料表面电化学析氢反应的影响(Yan et al. 2017).

在此基础上Wang 等 (2019)通过外加应力调控Ni3Fe 薄膜的OER 性能. 该报道揭示了在Ni3Fe(111)晶面上的氧对提高OER 活性具有重要作用, 并且这种现象可以用d 带模型很好地解释. 作者通过理论计算和实验指出单轴拉伸应变可以提高Ni3Fe 薄膜的OER 活性, 降低其过电势: 具体为0.4%的拉伸应变可有效使过电势降低7.3 mV. 此外, Niu 等 (2020)通过理论与实验相结合证明了机械应力可以原位调控甲酸分解, 第一性原理预测压力可以降低过电势, 拉力与此相反; 通过拉伸载荷原位调控甲酸分解, 实验证明大约0.4%的压应变可以降低75 mV 的过电势, 进而原位调控甲酸分解路径. 这些工作为设计合成新型非贵金属催化剂用于电催化提供了新的思路和策略.

除外载荷导致的拉伸应变外, 弯曲基底可以将应变引入二维薄膜材料中, 进而研究应变作用下材料化学性质. Lee 等 (2014)使用这种方法来提升二硫化钼(MoS2)二维催化剂的HER 活性,如图12 所示. Lee 等 (2014)将真空过滤的二硫化钼薄膜打印在银涂层的PET 基底上. 通过弯曲PET 基底可以对沉积在基底上的二硫化钼膜施加大小约为0.02%的弯曲拉伸应变. 与无应变曲线相比, 拉伸应变导致 MoS2的析氢反应极化曲线明显更陡, 这与DFT 计算得到的d 带模型结果相一致. 当拉伸应变从0 增大到0.02%时, 电流密度从31 mA/cm2增大到48 mA/cm2, 如图12(b)所示. 这种机械弯曲方法能够实现二位薄膜材料的应变状态变化, 然而其应变量有限, 因此仅能有限地增强材料的电化学催化性能.

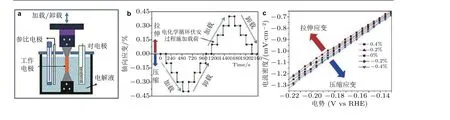
图11(a)电化学过程静载荷加载装置示意图, (b)电化学循环伏安过程的加载与卸载, (c)不同拉伸和压缩应变对电化学性能的影响 (Yan et al. 2016)

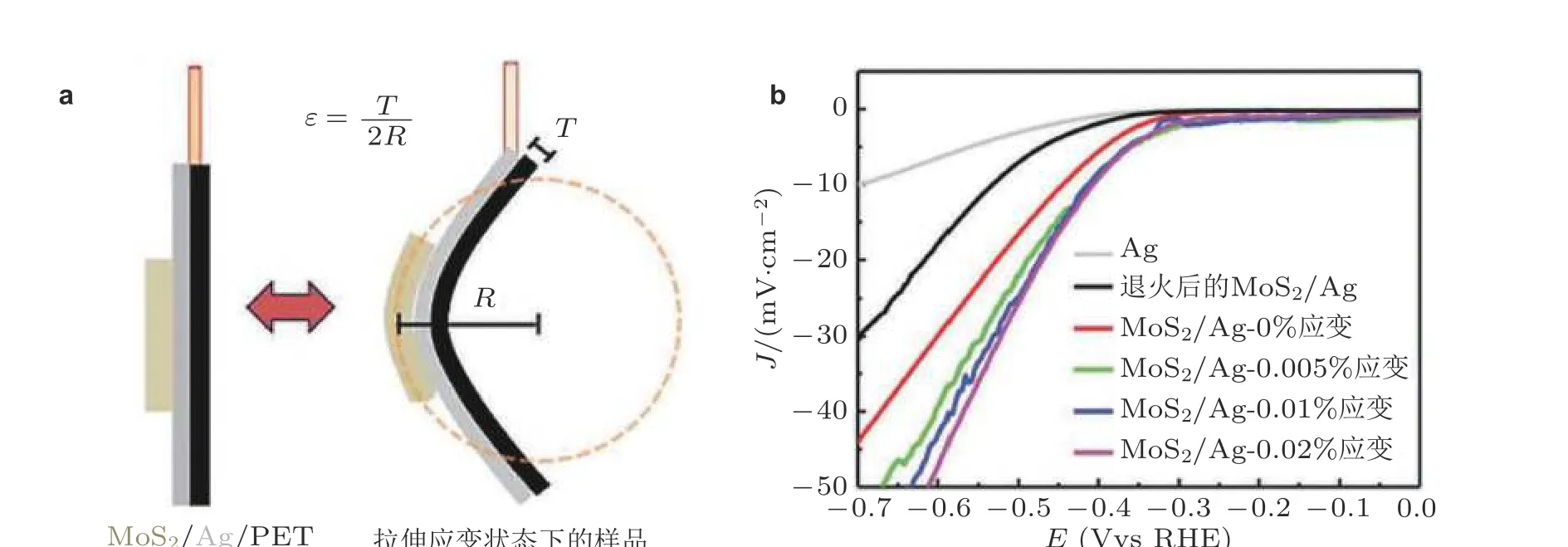
图12(a)通过弯曲Ag/PET 基底将应变引入到二维材料, 其中R 为弯曲半径, T 为PET 衬底厚度, ε =T/2R 为估算的应变大小; (b)与应变相关的析氢反应极化曲线 (Lee et al. 2014)

值得注意的是, 电催化反应过程是一个复杂的电化学动态过程, 在反应过程中氧空位、缺陷等材料本征因素将与晶格应变共同影响材料的催化活性, 目前存在着电催化反应过程中电化学诱导材料本征活性的变化与静态应变导致的活性变化无法准确区分的难点. 此外, 电催化反应过程通常包括两个部分: 电容充放电过程(capacitive process)和法拉第电子交换过程(Faradaic process).在电容充放电过程, 电极-电解质界面相当于一个电容器, 产生的电流称为电容电流; 电化学反应会发生电子转移和交换, 从而产生反应电流, 也称为法拉第电流, 只有法拉第电流描述催化反应速率. 而以上介绍的应变与催化活性关联性实验中得到的仅仅是静应变对总电流的影响,而不是化学反应的法拉第电流.

3.4 交变载荷作用

基于常规实验手段可知, 应变确实可以影响金属材料的电化学反应过程, 但是具体影响规律和物理机理仍不清楚, 主要由于传统的应变生成策略具有以下几个缺点: (1)活性层原子除了受到静态晶格应变作用以外, 在研究中还会受到配位效应、氧空位、缺陷等其他材料本征因素的干扰; (2)无法准确区分应变对于电催化反应中电容过程和法拉第过程的不同作用机制; (3)纳米材料晶格畸变诱导的应变值难于精确定量, 缺少实时的可调控性.这些难点都限制了对应变-活性相关性的精准识别和规律探索.

相比于静载荷和传统的材料制备手段, 交变载荷具有幅值和频率的可变性以及连续的调控性, 而噪音、缺陷、空位、配位效应等其他外部或材料本征的影响因素在时间和幅度变化上都是随机发生的, 因此, 在实验中采用交变载荷的力学方法可以在实验中完全排除其他干扰因素的影响. Smetanin 等 (2009)采用动态载荷的方式研究了应变对Au 电极在10 mmol/L 的 HClO4电解液环境中开路电势(open circuit potential, OCP)的影响, 测试结果如图13 所示. 所加载的应变(ε)以及电极在电解液中的开路电势(E)在时间轴上呈现出相同周期变化关系. 以应变(ε)为自变量, 开路电势(E)为因变量, 可以清楚地看到开路电势与应变呈现出极好的线性负相关性,其斜率为应变下电极OCP 的变化量, 即前文提到的电势-应变响应系数(ς)值. 然而, 这种实验测量方法只能在满足开路条件下有效, 即电化学体系中没有电流. 如果所研究的电化学体系不满足开路的条件, 在恒电势仪的作用下, 电流将直接快速的补偿由外应变所引起的电势变化, 无法测量电势的变化量, 因此这种方案不能直接运用到实际的电化学反应过程.

随后, Smetanin 和Deng 对实验方案进一步升级完善(Smetanin et al. 2011, Deng 2014), 通过在外电路增加额外的电阻来延迟电流对振荡电势的补偿过程, 然后基于锁相技术将与应变激励信号同频率响应的电化学电势信号精准地提取出来, 最后利用频率响应的差异来解耦法拉第电流和电容电流在交变载荷下的不同响应机制. 这种基于交变载荷的研究方案称为动态力-电-化学耦合分析方法(dynamic electro-chemo-mechanical analysis, DECMA): 通过压电陶瓷驱动器对薄膜样品施加水平方向上正弦函数变化的交变载荷, 在该交变载荷作用下样品表面产生形变; 控制外部交流电压的大小来调节压电陶瓷所施加的载荷大小, 使薄膜形变处于弹性范围之内. 图14是关于电极的电势-应变响应和电流-应变响应的测量示意图以及相对应的响应信号, 可以清楚地观察到电极电势和电流的响应信号随着交变应变信号的变化而变化, 并具有和应变信号相同的变化频率. 据此, 在实验上可以独立地观察和准确地测量出应变对电化学过程中电势和电流这两个物理量的影响.

实验方案采用应变片测量手段实时记录由动态外载所诱发的样品表面形变的变化信号, 并以表面应变为自变量, 研究在不同电化学环境下表面应变对电势或者电流的影响. 由于动态的电势响应信号(ΔE)、电流响应信号(ΔI)与交变载荷导致的应变信号(Δε)具有相同的变化周期或频率, 利用数字锁相放大器将深埋在各种信号中具有相同频率的电化学动态响应信号提取出来,获取电势和电流关于应变信号的响应幅值和相位等数据信息. 锁相放大器的主要功能是其相敏检测核心技术, 利用与待测信号具有相同频率和固定相位关系的参考信号为基准, 滤除与参考频率不同的噪声, 从而提取出有用的幅值和相位等信息. 例如, 将应变信号ε=εˆ sin(ωt)作为参考信号, 待测电化学信号为S(t),锁相放大器经过差分模式后输出的信号为

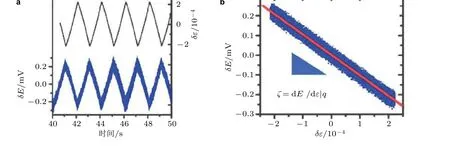
图13(a)动态应变以及电极在电解液中的开路电势随时间的变化关系, (b)开路电势与应变呈现出极好的线性负相关性 (Smetanin et al. 2008)

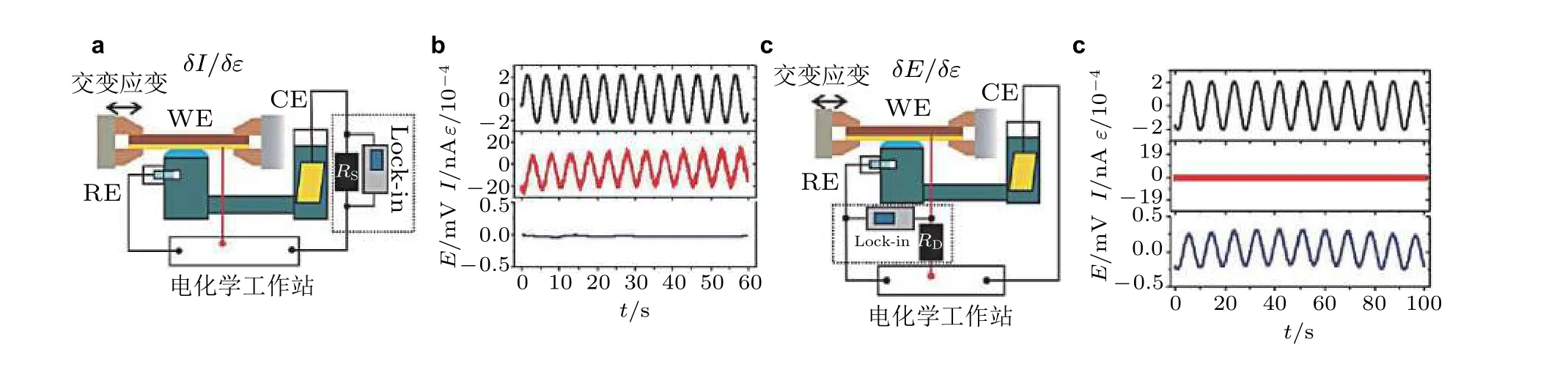
图14交变载荷作用下应变效应研究平台电路示意图. (a)电极电流−应变响应; (c) 电极电势−应变响应. WE 为工作电极, 即金属薄膜; RE、CE 分别为电化学实验中的参比电极和对电极; Lock-In 为锁相放大器.(b)和(d)分别为动态机械应变诱导的电流、电势响应信号, 其中横坐标为测量时间, 各个纵坐标分别为应变ε、 电流I、电势E (Smetanin et al. 2011, Deng 2014)

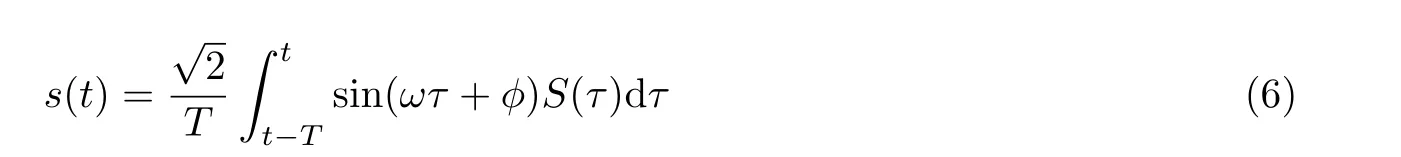
当φ= 0 时, 式(6)的结果是应变作用下电化学响应信号的实部,φ= π/2 时所对应的是应变作用下电化学响应信号的虚部. 因此, DECMA 研究方案除了可以获得应变作用下电化学电势或电流信号的响应大小, 还能提供应变信号与电化学电势或电流信号之间的相位差, 这些重要信息在传统电催化活性应变效应研究方案中很难获取.

基于DECMA 交变载荷的实验方案, 研究人员针对外应力引起的应变对于电化学过程影响的物理规律已开展了一系统的研究工作. 目前已应用于研究电容充放电过程(capacitive process);氢离子(H+)、氢氧根(OH-)以及铜离子(Cu2+)在不同金属电极表面的电化学吸附过程(Deng &Weissmüller 2014; Deng et al. 2015a, 2015b; He et al. 2017; Deng & Yuan 2019); 机械调控电极表面氢析出电化学反应的反应电流, 并对于氢析出反应建立了考虑表面应变耦合的动力学修正模型(Weissmüller 2013, Deng et al. 2014).

4 交变载荷下表面应变对电化学过程的调控

在电化学过程中, 工作电极的反应包括两个重要过程: 法拉第过程(Faradaic process)和电容过程(capacitive process). 法拉第过程是指在电极表面发生氧化还原反应的过程, 并且在电极与溶液界面上有大量的电子转移过程. 电容过程是指在电极与溶液界面上虽然没有电荷转移, 但是伴随着电势变化的过程导致双电层的充放电, 进而引起电流的流动和变化.

4.1 交变载荷作用下应变对电化学电容过程的影响

以H2SO4电解质溶液中Au 表面电化学电容充放电过程为例, 实验中Au 表面受到正弦周期性变化的应变作用时, 电流信号呈现出振荡(图15(a)), 将电流响应信号与应变信号相比较, 可以看出二者具有相同的变化频率(图15(b)), 通过前文介绍的锁相技术, 可以得到交变应变作用下电流响应信号的幅值和相位情况(图15(c)).由此可知: 在电容充放电过程中, 应变对电流作用大小与电极电势(E)密切相关, 并呈现出最大值(Smetanin et al. 2011, Deng & Yuan 2019).

Deng 和 Yuan (2019)以电流-应变响应系数Λ(E)达到最大值所处的电势作为恒定的电势(E= 0.6 V), 进一步研究响应系数Λ与应变频率的相关性(图16). 系数Λ的实部随应变频率的增大而增大. 当应变频率大于60 Hz 时,Λ实部趋于饱和值. 而系数Λ的虚部值随应变频率的增大先增大后减小, 在应变频率约为15 Hz 时,Λ虚部值达到最大.Λ的相位差随着应变频率的增大而减小, 从80°减小到10°. 由此看出电化学过程的电流变量与应变频率之间呈现出复杂的映射关系,而这些重要的信息没法在传统材料手段得到的静态晶格应变以及静载荷作用的实验中观察到.

为了进一步探索金属-电解质界面的电流-应变响应的机理, Deng 和 Yuan (2019)建立了一个等效电路模型(图16(a)插图所示).由于金属-电解质界面属于电容充电, 没有法拉第过程, 因此等效电路模型中没有与电荷转移相关的损耗. 考虑正弦变化的交变应变,ε=εˆ sin(ωt), 其中ε^表示应变的大小, 角频率ω与应变频率υ的关系为ω= 2πυ. 由于不包括法拉第过程电荷转移的相关损耗, Au 薄膜电极在应变状态下, 其电极表面电势的响应遵循

式中ς为前文提到的电势-应变响应系数, 被定义为ς= dE/dε|q,E0表示无外应变作用的电极电势. 在等效电路模型中, 包括了弹性应变引起电势变量, 关系式为

在金属-电解质界面, 弹性应变引起相位移(φ), 在此状态下的电流可以表达为

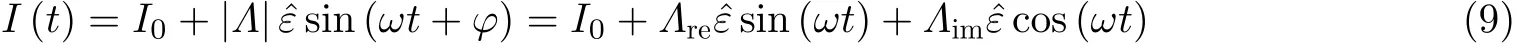
图15(a)交变应变作用下循环伏安测试的电流响应信号(I)在时间域(t)的变化, 电极电势扫速为10 mV/s, 施加应变频率υ = 20 Hz, 其中蓝色实线为没有应变作用的常规电流变化情况; (b)恒电势下示波器同步记录的电流变化和频率为2 Hz 的应变信号; (c)基于锁定测量技术得到的电流−应变响应系数的幅值和相位结果 (Deng & Yuan 2019)

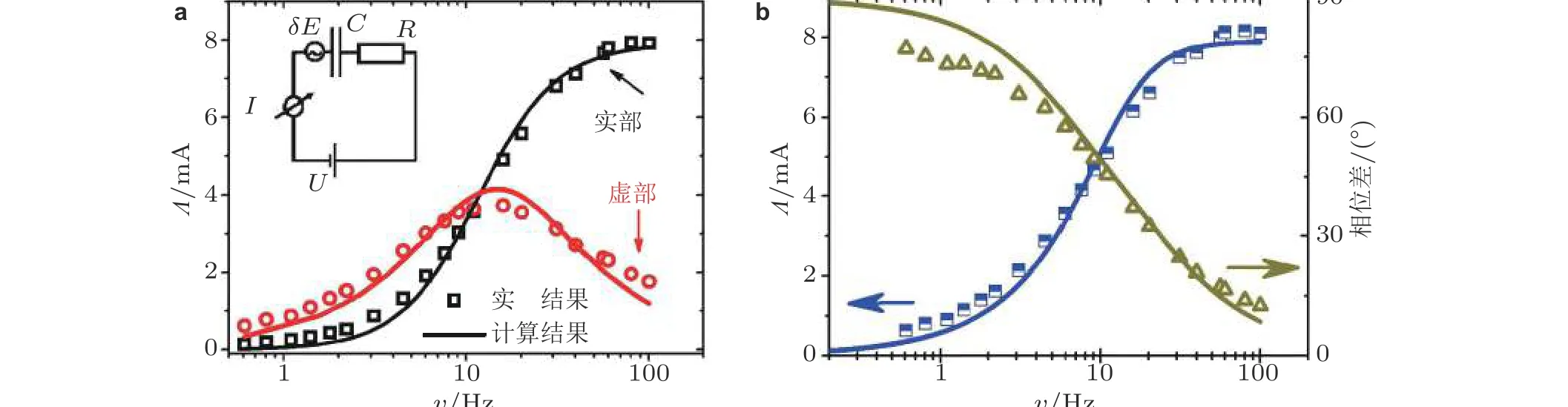
图16(a)在电势为0.6 V 时, 电流−应变响应系数(Λ)实部、虚部与应变频率υ 的函数关系, 插图中金属−电解液界面等效电路模型; (b)电流−应变响应系数(Λ)的幅值和相位移分别与应变频率υ 的函数关系. 图中散点为实验数据, 实线为等效电路模拟结果 (Deng & Yuan 2019)

Λre和Λim分别代表电流-应变响应系数的实部和虚部. 基于基尔霍夫电路定律, 分析等效电路模型中的金薄膜电极电势的变量ΔE(t), 电流-应变响应系数Λ的相关表达式为

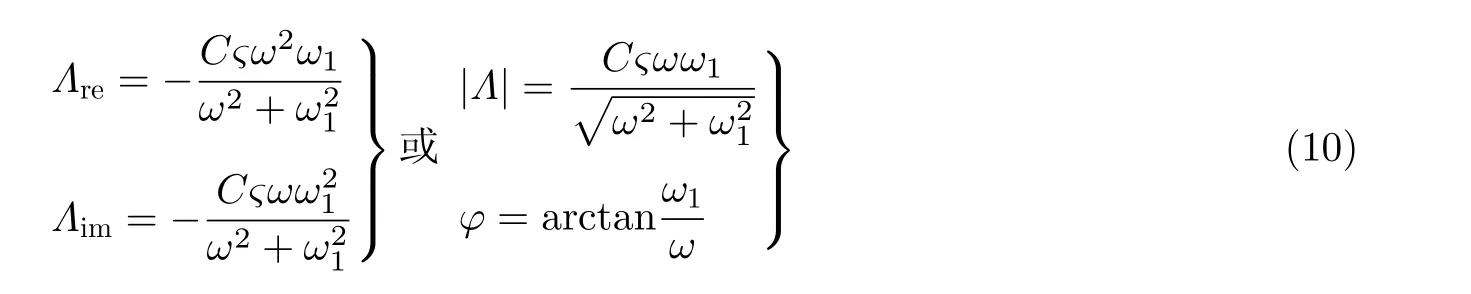
（10）式中,ς为电势-应变响应系数;C为双电层电容;ω1为RC电路时间常数的倒数, 即ω1=1/RC; R为固液界面的电阻. 理论表达式(10)很好地描述了实验中观察到的电流-应变响应系数(Λ)的幅值和相位移分别与应变频率υ的关系(等效电路模拟结果如图16 实线所示).

对于电势-应变响应系数(ς), 传统观点认为ς在某一个规定的电化学体系是一个恒定的常数, 与电化学过程的电极状态无关. 图15(c)表明电流-应变响应系数Λ与电极电势E相关, 而根据式(10)得知Λ与ς存在着关联性, 因此ς 必然是与电极状态(E)密切相关的变量. 目前有两个实验方法测定参数ς值: (1)基于电流-应变响应系数, 需要获得固液界面的阻抗信息, 进而间接得到ς(式(10)); (2)基于DECMA 锁相技术将与应变激励信号同频率响应的电势信号精准地提取出来.以上两种方法的实验结果如图17 所示. 由此, 在实验中验证了系数ς 是一个与电极表面电势E密切相关联的函数, 即ς=ς(E); 对所研究的电化学体系10 mmol/L 的 HClO4溶液中Au薄膜表面的电化学电容过程, 系数ς整体呈现出负值, 并具有一个极值点, 该ς(E)峰值所在的电势与零电荷电势(potential of zero charge, PZC)相重合(Smetanin 等 2011).零电荷电势的传统实验定量方法对电极表面平整度等许多因素具有较为苛刻的要求, 因此采用力学交变载荷测定ς(E)峰值的方法可以作为定量测量固液界面零电荷电势值的一种新方案.

除了金属电极材料外, 具有无定性结构的碳布材料在机械拉伸作用下性能同样会发生变化.最新的实验结果表明无定性结构的碳布材料在机械拉伸下其比电容有所下降(Zhang et al. 2018).根据超级电容器领域通用的电极能量密度(energy density)的计算公式:w= 1/2Cs (ΔE)2, 其中ΔE是电极的工作电压窗口,Cs 是比电容值, 而上述的研究结果表明ΔE和Cs 都是与应变相关的物理参数, 因此通过表面力学行为可以进一步较大程度改善超级电容器电极的性能, 如能量密度等.

4.2 交变载荷作用下应变对电化学吸附过程的影响

电化学吸附过程(eletrosoprtion processes)在电极表面整个电催化反应中具有非常重要的地位, 而应变能够直接影响离子在电极表面的吸附焓, 但材料制备的实验手段无法定量化描述应变的作用. 基于DECMA 交变载荷的实验方案, Deng 和 Weissmüller (2014)研究了金属电极表面(Au, Pd)的不同离子吸附过程, 发现电势-应变响应系数的特征与吸附物种类密切相关(ςad=dEad/dε), 如图18 所示: 对于H+吸附,ςad＞ 0; 对于OH-吸附,ςad＜ 0. 系数的正负号具有完全不一样的物理意义: 正号表示拉应变 (ε＞ 0) 可以提高氢的吸附电势; 负号则刚好相反, 拉应变降低氢氧根的吸附电势. 通过前文中的理论分析和推导, 电化学吸附过程中的吸附焓Δhad和外载应变之间的数学表达式为: dΔhad/dε= -zFςad. 根据ςad的物理意义, 可以得到以下结论: 拉应变可以降低氢离子(H+)和氢氧根(OH-)在金属电极表面的吸附焓. 因此, 通过外应力调控的应变可以改变离子在电极表面的吸附能; 根据应变影响吸附能的具体表达式, 进而定量预测吸附能在不同应变下的变化程度.

4.3 交变载荷作用下应变对电化学沉积过程的影响

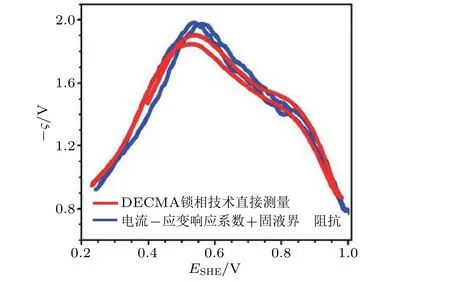
图17电势−应变响应系数(ς)的两种测量方法比较: DECMA 锁相技术直接测量(红色曲线)以及通过电流−应变响应系数与固液界面阻抗信息(蓝色曲线). 电化学体系: Au 薄膜在10 mmol/L 的HClO4 溶液中. (Smetanin et al. 2011)

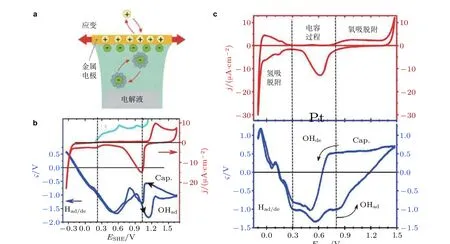
图18(a)电化学吸附过程的示意图; 氢离子(H+)和氢氧根(OH−)在金属Au 电极表面(b)、Pt 电极表面(c)吸附过程的响应系数ς(E). 图中Had/de 表示氢吸脱附, OHad/de 表示氢氧根吸脱附, Cap.表示电容过程. (Deng & Weissmüller 2014)

除了溶液中离子的电化学吸附外, 电化学沉积(electrochemical deposition)一直被材料和化学界的科研人员用于制备新型功能材料, 其中最为典型的是铜(Cu)在金表面的欠电势沉积过程(under potential deposition, UPD). 针对铜在金表面电化学沉积不同阶段的应变作用, Yang 等(2017)定量分析了Cu UPD 过程系数ς的变化规律, 将铜电沉积电势E与外应变ε相关联, 研究结果表明每个电极过程都可用一个相应的独立系数ς～来表征, 而在复杂的电化学过程中, 应变的具体作用可以由各自独立响应系数根据它们的相对贡献加权获得. 图19(a)的实验结果表明: 在铜电化学沉积的第一阶段, 此过程为铜原子和硫酸根蜂窝结构的形成, 其响应系数,ς≤ 0, 是由于铜沉积过程和硫酸根吸附过程相互竞争所导致的. 而在铜电化学沉积的第二阶段,ς＞ 0, 此过程对应于铜原子单层的形成过程. 同样根据吸附焓Δhad和外应变ε之间的数学表达式: dΔhad/dε=-zFςad, 可知拉伸应变可以促进铜单原子层的形成. 在实验研究中还观察到ς关于应变频率的依赖性(图19(b)): 在E= 0.6 V 时(Au 表面的电容充电过程),ς呈现与应变频率的弱相关性;在Cu UPD 的两个阶段(E= 0.5 V,E= 0.25 V),ς值随应变频率的降低而增大. 这种应变频率依赖性表明不同电化学过程存在竞争关系. 高频区由赝电容过程控制, 低频区由Cu 电沉积过程控制. 在UPDⅠ阶段(E= 0.5 V), 在较低的频率下,ς趋于零. 在UPDⅡ阶段(E= 0.25 V),ς在应变频率低于20 Hz 时趋于饱和值为+ 0.45 V.

除了ς幅值大小以外, Yang 等 (2017)在实验中还观察到了不同电极过程ς的相位差随应变频率的变化规律(图19(c)). 对于电容过程(E= 0.6 V), 电势响应信号与动态应变信号的相位差约为+ 170°, 与应变频率存在弱相关性. 在Cu UPDⅠ阶段(E= 0.5 V), 相位差由高频时的+ 180°减小到低频时的+ 100°. 在Cu UPDⅡ阶段(E= 0.25 V), 相位差由高频时的+ 90°减小到低频时的0°, 并当频率小于20 Hz 时, 相位差基本稳定在0°. 因此, 通过测量与应变频率的相关性可以区分不同电极过程的应变作用, 经典金属电化学欠电势沉积过程可以通过交变载荷作用下的动态应变进行精准调控.

4.4 交变载荷作用下应变对电化学法拉第过程的影响

在电催化过程中往往会伴随着双电层电容电流, 而只有法拉第反应电流描述电化学反应速率, 因此如何区分弹性应变对电容电流和法拉第电流的影响, 一直是应变影响反应速率机理研究中的一个难点.基于交变载荷的方案, Deng 等 (2014)以H2SO4电解液环境的Au 和Pt 电极表面电化学析氢反应为研究对象, 在电极材料上施加弹性应变原位测量反应电流的响应, 进而探讨晶格参数的变化对电催化活性的影响. 首先通过理论分析得到交变载荷作用下,ε=εˆ sin(ωt), 应变对总电流作用的数学表达式

在低过电势ΔE时(E= -0.4 V ～ -0.2 V), 拉伸应变会增大反应电流密度继而提升金属的析氢反应活性, 而在高过电势时(E＜ -0.4 V), 则呈现出相反的趋势, 金属的反应活性降低. 传统描述电极反应过程的动力学模型并没有考虑应变的作用, 无法解释或预测表面应变对电化学反应活性的影响规律. Deng 等(2014)随后对传统的析氢反应动力学方程关于应变项进行修正.

图19(a)铜在金电极表面电化学沉积过程响应系数ς 与电化学信号、铜原子覆盖度之间的关系; 不同电化学过程响应系数ς 的幅值(b)、相位差(c)与应变频率的关系 (Yang et al. 2017)

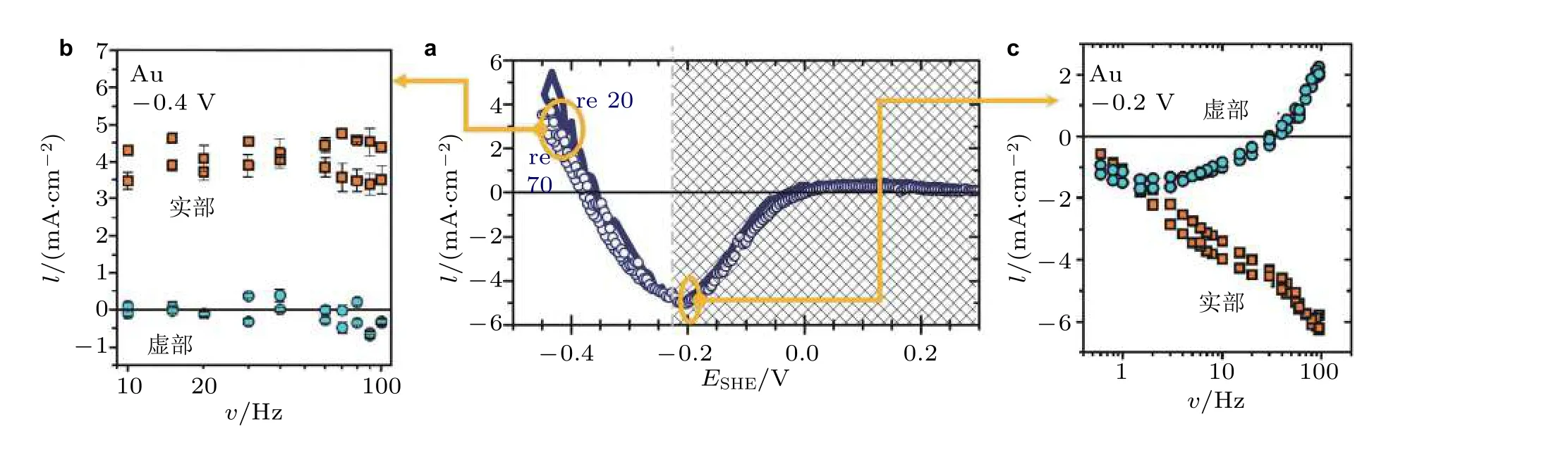
图20区分应变对反应电流和双电层电容电流作用的实验结果. (a)反应电流−应变参数 ι 在电化学析氢反应的变化规律, (b)析氢反应占主导时实部和虚部与应变频率的关系, (c)电容过程占主导时实部和虚部与应变频率的关系, 电化学体系为Au 在0.5 M H2SO4 中 (Deng et al. 2014)

式中, 活化焓Δhex是与质子和吸附氢相结合的活化能垒(能量势垒)相关, 其定义表述为图21(a)所示. 基于Langmuir 吸附等温线, 氢表面覆盖度由氢吸附焓(Δhad)所控制(Gennero de Chialvo &Chialvo 1994, Kibler 2006)

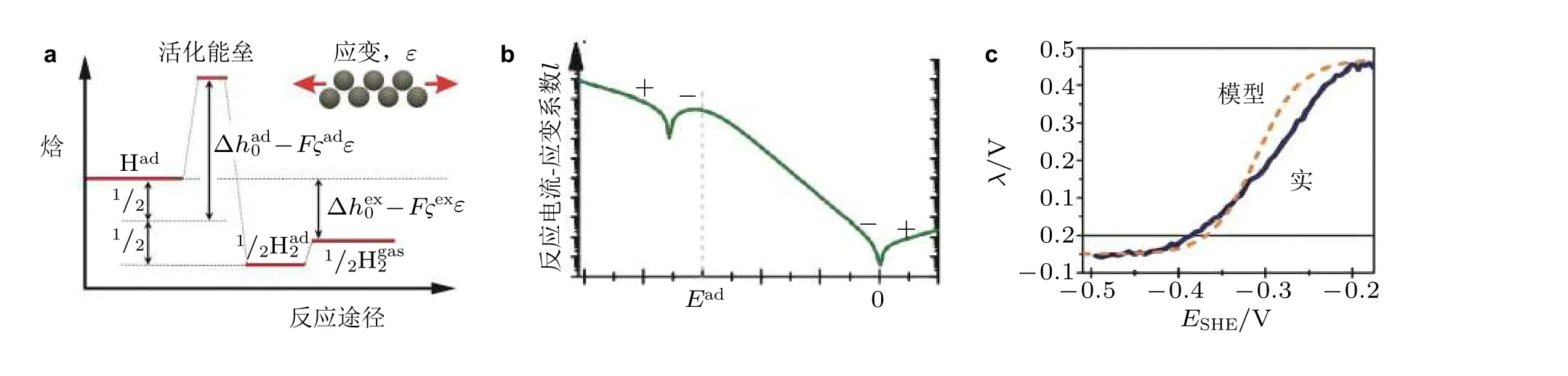
图21(a)应变在电化学析氢反应中的作用主要影响吸附焓以及活化焓, (b)数学模型预测的反应电流−应变参数随着电极电势变化规律, (c)表面应变对氢析出电化学反应影响的实验和模型结果对比图(Deng et al. 2014)

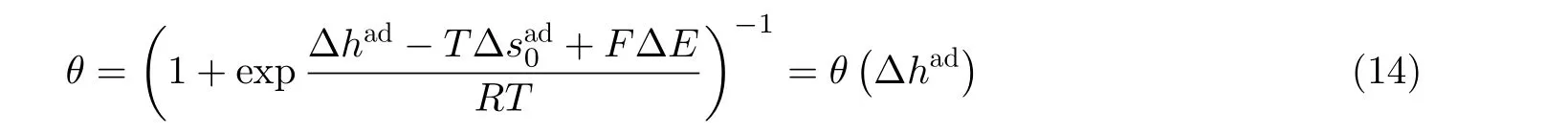
目前一系列实验已证实吸附焓(或吸附能)与应变密切相关. 因此, Deng 等 (2014)分别引入两个系数ςad和ςex来描述应变对吸附焓和活化焓的作用

表达式（17）包含了与应变相关的吸附焓和活化焓的耦合系数ςad和ςex. 随着过电势的增大,氢在催化剂表面的覆盖度(θ)越来越大, 反应电流-应变响应系数(ι)的符号也由负变成正(图21(b)),这解释了前面所观察到的实验现象(图20(a)).

为了进一步简化数学表达式, Deng 等 (2014)定义了反应活性-应变响应系数λ 来量化法拉第电流对应变响应的相对变化量

5 展 望

近年来, 应变工程在电催化领域的应用受到了越来越多的关注. 在实验方面, 基于活性层与基底材料晶格不匹配来产生晶格应变策略可以产生较大的应变作用, 然而这些新型电催化剂材料的制备工艺较为繁琐, 必然增加材料的制备成本. 另外, 纳米材料晶格畸变诱导的应变值难于精确定量, 缺少实时的可调控性.要解决这个问题, 需要表面应变的可控技术, 而这方面恰恰属于力学领域的强项. 我们认为今后载荷作用下应变工程提升电催化性能的研究方向主要有以下几个方面:

(1) 通过载荷的施加方式可以精确地定量材料表面的应变大小. 根据电化学信号与交变载荷频率的相位差信息可以区分开电化学诱导材料本征活性的变化与静态应变导致的活性变化, 并解耦析氧反应中电容电流与法拉第电流的应变效应, 准确地获取应变在不同电化学阶段的物理规律; 这种方式适合于对反应机理的理解, 但目前应变值偏小, 不能大幅度提升材料的电催化性能.

(2) 如果施加较大的交变载荷作用下, 材料本身极有可能涉及到疲劳失效等问题, 材料疲劳失效与电化学催化反应活性之间的耦合关系将更为复杂, 需要通过理论、计算以及实验等多方面深入系统的研究.

(3) 外载荷可以实现活性层材料应变的精准调控, 与外载荷相关联的电催化反应力催化耦合理论将是链接力学与电催化之间的理论桥梁, 然而目前在这方面的理论研究较少. 电化学领域中, 描述反应速率的动力学方程时没有考虑力催化耦合作用, 难以充分揭示力学与催化之间的内在关系, 需要基于力催化耦合参数的实验数据, 在理论分析上考虑外应变与电化学过程诱导本征应力的相互作用, 在相关的反应方程中添加力催化耦合项.

(4) 此外, 目前描述固液界面力催化耦合理论的热力学表述中忽略了热的因素.在理论上除了考虑力学载荷因素外, 还需要在传统反应动力学方程中考虑电催化过程所产生的热量因素, 深入研究电催化过程的热-力-电-化学耦合关系, 揭示其作用机理.

(5) 在力学领域常用的数值仿真模拟手段将是力催化耦合研究中不可缺少的关键环节, 通过与第一性原理计算相结合, 对材料微结构设计进行优化. 基于固体力学的理论框架和模拟计算,合理设计电催化剂表面微结构阵列, 旨在实现载荷作用下应变场可控化, 是提升电催化剂性能的一个重要途径.

致 谢 国家科技重大专项(2017-Ⅶ-0011-0106)、国家自然科学基金项目(12172118, 11602171,U1864208)、河北省自然科学基金创新群体研究项目(A2020202002)、河北省研究发展重点计划(202030507040009)、中央引导地方科技发展资金项目(216Z4402G) 、天津市自然科学基金重点项目 (S20ZDF077) 、天津市科技计划项目(20ZYJDJC00030)和河北工业大学“元光学者”人才项目资助.