人体肌骨的多柔体系统动力学研究进展

郭建峤 王言冰 田 强 任革学 胡海岩

1 北京理工大学宇航学院, 飞行器动力学与控制教育部重点实验室, 北京 100081 2 清华大学, 航天航空学院, 北京 100084

1 引 言

人体肌肉骨骼系统简称肌骨系统(musculoskeletal system), 包括骨骼、骨骼肌与骨连接, 其质量占人体总质量的50%以上(郑思竞 1983). 骨骼构成人体的支架, 起到支撑、保护内部脏器的作用. 骨骼肌包裹在骨骼外部, 通过附着点与骨骼连接, 并受神经支配; 它既是人体运动的原动机(Fung 1993), 又维持人体在外部载荷作用下的力学稳定性. 骨连接包括关节与辅助结构两部分. 辅助结构主要由结缔组织构成, 其中, 韧带维持关节局部稳定性, 避免关节脱位; 软骨起到润滑关节、缓冲冲击载荷的作用. 从力学角度看, 人体肌骨系统是典型的多柔体系统(Alizadeh et al. 2020), 其骨骼肌、韧带等运动部件均具有大范围相对运动和变形耦合的动力学特征(Shabana 1997).

1.1 学科发展概述

人体肌骨系统动力学(musculoskeletal dynamics), 主要研究人体在运动过程中产生的时变肌肉内力、关节力矩及产生的动力学影响, 包括生物组织变形/失效、人体做功、人体与环境相互作用等 (Yamaguchi 2005). 人体肌骨系统动力学建模与分析技术的进步, 离不开近年来运动生物力学实验手段的蓬勃发展. 目前, 研究者已能够通过动作捕捉实验获取人体运动过程中的三维关节运动, 测量各足所受合力、合力矩与足底压力空间分布, 同时采集靠近皮肤的表面肌群受神经控制产生的生物电信号(Winter 2009), 即表面肌电 (electromyography, EMG) . 然而, 由于人体系统的复杂性以及科技伦理因素, 仅凭人体动力学实验无法完全解释人体运动系统的神经与肌肉控制及肌肉驱动、承载与做功机制. 因此, 研究人体动力学仍强烈依赖计算机仿真手段.

自20 世纪90 年代以来, 力学界已初步构建起人体肌骨多体动力学建模的基本范式 (Hicks et al. 2015). 鉴于骨骼是由胶原蛋白与羟基磷灰石构成的生物复合材料(Fratzl 2007), 在绝大多数肌骨模型中将骨骼简化为刚体, 仅在存在骨折风险(Kłodowski et al. 2012)时考虑其柔性小变形. 骨骼肌与其他生物软材料不同, 即便不发生变形, 其内部肌原纤维亦能在神经刺激下通过滑动产生主动肌力(Hill 1938, Fung 1993). 骨骼肌的其他组织, 包括筋膜系统、肌腱等, 具有超弹性本构关系, 仅能在被动拉伸条件下产生内力. 因此, 已有肌骨模型一般将骨骼肌用Hill、Zajac 模型(Hill 1938, Zajac 1989)描述, 包含主动收缩元件与串、并联被动拉伸元件. 此外, 通常将韧带、软骨等骨连接辅助结构视为超弹性体, 用非线性弹簧建模(Blankevoort et al. 1991), 从而实现动力学模型与肌骨系统解剖特征的对应.

目前, 力学界已开发出一系列肌骨动力学模型与计算软件. 其中, 最具代表性的肌骨模型是Stanford 大学Delp 教授团队建立的开源模型“OpenSim” (Seth et al. 2018), 如图1(a)所示. 截至2021 年11 月, 这一模型的下载量已达到438 111 次, 是目前最受关注的人体力学模型. 丹麦Aalborg 大学建立的Anybody 模型如图1(b)所示, 其肌肉解剖精度达到肌束级, 并在脊柱(de Zee et al. 2007)与口腔(Andersen et al. 2017)建模等方面具有优势. 美国LifeModeler 公司依靠商业软件MSC Adams 开发了LifeMOD 插件, 参见图1(c). LifeMOD 已被世界著名医疗器械公司施乐辉收购, 专门应用于人工关节数字化设计. 如图1(d)所示, 加拿大British Columbia 大学针对人体口颌系统开发了“ArtiSynth”工具(Lloyd et al. 2012), 在肌骨模型中引入大变形柔性单元, 实现了面部(Stavness et al. 2011)、舌(Stavness et al. 2012)等软组织与肌骨系统耦合仿真. 然而, 这些模型均基于西方人的解剖数据建立数据库, 其模型参数无法真实反映中国人肌骨系统具有的独特属性(例如: Lu Y et al. 2020), 肌肉生物力学参数亦偏离大多数健康中国人的参数范围. 此外,上述肌骨动力学模型的求解内核不完全对普通研究者开放, 难以根据研究需求调整或实现复杂问题的计算.

图1人体肌骨系 统 多 体动力学模 型. (a) OpenSim 全人体模 型(Raabe & Chaudhari 2016), (b) Anybody 全人体模型(Bassani et al. 2017), (c) LifeMOD 全人体模型(Kia et al. 2014), (d) ArtiSynth 口颌模型(Stavness et al. 2011)

与机械系统动力学不同, 人体肌骨多柔体系统动力学的多数研究需求解逆动力学 (inverse dynamics) 问题. 逆动力学一般需通过实验手段测定人体关节运动与外载荷, 分别作为肌骨模型的运动学与外力输入, 求解肌肉内力与神经与肌肉控制问题. 这一方法的主要难点在于如何处理关节肌肉控制的冗余性 (redundancy) . 冗余性是指人体关节的某一运动自由度同时受多条肌肉控制, 满足关节动平衡条件的肌肉内力分配模式可能有无穷多组, 但神经与肌肉控制应满足某一确定规律. 为了确定不同肌肉的内力, 绝大多数研究将肌肉的冗余控制视为求解最优化问题, 即假设真实肌力分配应实现某一生理量最优. 然而, 人体运动应满足哪一优化目标, 尚未有确定答案(Ackermann & van den Bogert 2010). 另外, 肌骨动力学仿真预测的肌肉激活度 (muscle activation) 与实测表面肌电间仅在定性上相关, 定量上仍存在显著差异(Shourijeh et al. 2016; Kian et al.2019). 近年来, 部分学者开始尝试将研究转向正问题求解. 正向动力学 (forward dynamics) 以神经对各个肌肉的归一化激活水平作为肌骨模型输入, 即已知肌肉内力, 求解肌骨系统运动. 与逆向动力学相比, 正向动力学实现了从人体动作分析到动作预测的跨越, 但其受制于目前对人体解剖与神经与肌肉控制认识程度的局限性, 计算和分析方法尚不成熟.

如图2 所示, 人体肌骨系统动力学模型在临床医学、竞技体育、军事训练、人机工程等诸多领域具有广泛的应用前景. 例如, 在日常生活中, 肌骨模型可以与Kinect (Skals et al. 2017b)、Xsens (Karatsidis et al. 2019)等消费级传感技术融合, 监测跑步人群的下肢肌肉发力模式. 在矫形骨科领域, 肌骨模型可用于分析关节置换患者术后肌肉发力方式与关节接触载荷(Modenese &Phillips 2012), 判断术后出现二次脱位的潜在风险, 参见图2(a). 针对脊柱侧弯患者, 可根据其正侧位X 光片建立全脊柱肌骨模型(Jalalian et al. 2017, Shayestehpour et al. 2021), 帮助医生理解脊柱侧弯病情产生与发展的生物力学机制, 给出个性化康复训练方式. 在口腔颌面外科领域, 肌骨建模被用于分析口颌肿瘤患者手术切除部分下颌骨后出现的肌肉非对称发力模式(Hannam et al. 2010). 在神经康复领域, 肌骨动力学仿真结果有助于降低脑瘫患儿出现关节僵硬的可能性(van der Krogt et al. 2016), 参见图2(b). 在眼科领域, 肌骨模型能够帮助人们理解眼外肌对眼球运动的控制机制(Gao Z et al. 2014; Guo H et al. 2016; Guo H et al. 2019). 在体育工程领域, 很多学者将肌骨建模与动作采集相结合, 应用于运动员定量化动作分析, 实现高尔夫(Balzerson et al.2016)、场地自行车(Inkol et al. 2020)、越野滑雪(Vel Lace & Błażkiewicz 2021)等项目的数字化训练. 在军事领域, 美国军方资助建立了如图2(c)所示的“Santo”人体动力学模型, 优化士兵负重行走步态(Xiang et al. 2009, 2010). 在人机功效领域, 肌骨模型可被应用于外骨骼设计中, 分析手臂运动范围的可达域(Sartori et al. 2012). 如图2(d)所示, 肌骨模型仿真亦能应用于优化汽车座椅靠背(Zhang et al. 2019a, 2019b), 减小脊柱振动传递率, 避免脏器与脑部出现振动损伤.

1.2 我国研究现状

我国学者对人体动力学的研究始于20 世纪80 年代. 上海交通大学洪嘉振教授发表的《人体腾空运动的数学模型》(洪嘉振 1983), 标志着人体动力学研究在我国正式起步. 2006 年, 上海交通大学王成焘教授获得“中国力学虚拟人”国家自然科学基金重点项目资助(30530230). 该项目基于中国人体数据库建立了肌骨系统有限元分析与肌肉力预测平台(王成焘 2006, 唐刚等 2010),已在临床与人机工效等领域实现初步应用. 2015 年, 中国科学院大学孙应飞教授获得“人体运动生物力学测量、分析和模拟”国家自然科学基金重点项目资助(61431017), 建立了非最优激活条件下的骨骼肌Hill-Zajac 模型(Sun et al. 2018), 并实现基于EMG 预测上肢肌肉力(Hou et al.2016; Guo Y et al. 2019). 2021 年, 上海交通大学马少鹏教授获得“大范围快速骨肌运动过程的精细动作测量与能效分析”国家自然科学基金重点项目资助(12132009). 该项目旨在研究适合中国人的肌骨快速运动过程的运动特性测试与能效分析方法. 此外, 我国学者在骨生物力学领域也开展了系统研究, 代表性研究包括损伤防护(Wang et al. 2011)、内植物固定(Yao et al. 2020)、矫形康复(Wang et al. 2016)、骨细胞力学(Li et al. 2020), 等. 近年来, 我国学者已逐步将肌骨动力学建模与临床医学、竞技体育、人机功效等场景相结合, 其典型研究工作如下.

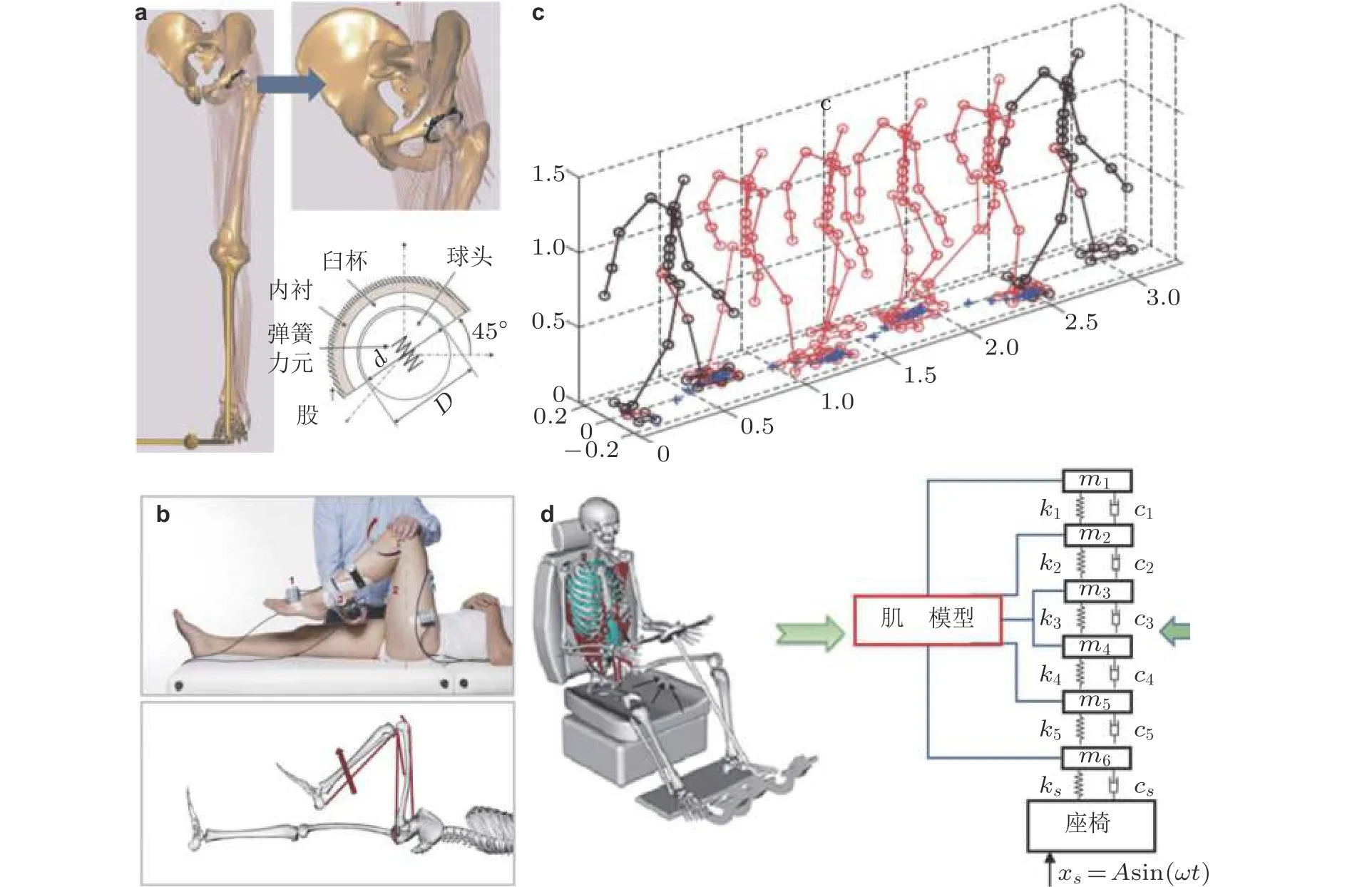
图2人体肌骨模型典型应用场景. (a) 人工髋关节假体设计(Zhang et al. 2015), (b) 脑瘫患儿关节僵硬缓解(Van Der Krogt et al. 2016), (c) 士兵负重步态(Xiang et al. 2009), (d) 汽车座椅减振(Zhang et al. 2019a)

(1) 骨伤科领域: 西安交通大学靳忠民教授团队(Zhang et al. 2015, Chen et al. 2016, Peng et al. 2018)将Anybody 模型与有限元结合, 基于关节接触分析设计下一代人工关节假体. 首都医科大学张宽教授团队基于OpenSim 模型评价全膝关节置换患者术后下肢功能变化(刘佳耕等2020). 北京大学荣起国教授等(Liu et al. 2020a, 2020b)基于肌骨动力学仿真结果提取正态度指标, 应用在前交叉韧带断裂的早期诊断.

(2) 康复医学领域: 上海交通大学王冬梅教授、王玮博士建立了腰椎肌骨模型(Wang et al.2020), 实现手法治疗效果定量评估(王玮等 2016). 同济大学牛文鑫等与香港理工大学张明教授合作, 实现椎间盘、韧带有限元模型与OpenSim 模型耦合(Wang et al. 2019). 太原理工大学陈维毅教授团队建立了下蹲动作膝关节软骨接触力的理论模型(Guo Y et al. 2012), 靳忠民教授团队建立了膝关节软骨损伤的有限元模型(林伟健等 2021). 最近, 王凡嘉等(2021)基于OpenSim 仿真优化深蹲康复训练方案. 南京体育学院钱竞光等(2015)针对偏瘫患者开展正-逆向耦合动力学分析(束一铭等 2017). 河南科技大学胡志刚等建立了个性化手部肌骨模型, 分析了脑卒中患者手部抓握肌肉力(赵梦文等 2021).

(3) 竞技体育领域: 北京体育大学李翰君等(2012, 2014a)建立了EMG 驱动的膝关节肌骨模型, 并提出了运动员骨骼肌参数个性化方法(李翰君等 2014b). 国家体育总局体育科学研究所郝卫亚等基于LifeMOD 模型, 优化跳马(李旭鸿和郝卫亚 2018, 肖晓飞等 2015)、平衡木(吴成亮等2016)等体操动作.

(4) 人机功效领域: 北京航空航天大学樊瑜波教授、王丽珍教授等(Wang et al. 2016,2018)将头颈部多刚体模型与有限元模型结合分析, 发现了避免飞行员着陆时颈椎冲击产生挥鞭伤的规律. 清华大学成波教授团队基于OpenSim 建立了驾驶员肌骨模型, 分析了人椅界面接触负载(孟祥杰等 2016)与脊柱振动传递率(Zhang C et al. 2019a, 2019b). 福州大学姚立纲、卢宗兴等基于Anybody 模型仿真结果定量设计了足部康复机器人摆幅(彭晨等 2021).

然而, 我国在肌骨系统这一多体动力学新兴领域的研究水平与欧美发达国家相比仍有一定差距. 例如, 据Web of Science 数据库统计显示, 截至2021 年11 月, 以“musculoskeletal dynamics”(肌骨动力学) 或“neuromusculoskeletal dynamics” (神经肌骨动力学) 为主题的论文共8558 篇, 其中ESI 高被引论文47 篇. 中国学者在本领域共发表论文391 篇, 全球排名仅第6 位; 与美国(5545 篇) 、英国 (759 篇) 、德国 (524 篇) 相比, 尚有明显差距. 又如, 在2021 年7 月举办的顶级会议“第28 届世界生物力学大会”上, 其“musculoskeletal modeling”分会场包含40 个口头报告, 而我国仅有本文第一作者参会介绍了多柔体动力学方法在骨骼肌弹性波传递领域的应用(Guo J et al. 2021b).

目前, 我国动力学研究领域的部分学者已将目光投向基于多体动力学理论的人体动力学研究. 例如, 大连理工大学齐朝辉教授建立了滑雪平面多刚体模型(Chen & Qi 2009), 并在MSC Adams 中建立了考虑主动肌力的髋关节肌骨系统模型(孙广艳 2006). 同济大学徐鉴教授团队忽略肌肉内力分配, 建立了人体与外骨骼耦合系统(张佳俊et al. 2021)与人体与假肢耦合系统(Ma et al. 2022)平面多刚体模型. 近年来, 北京大学王雪峰、上海交通大学马道林等学者分别针对手术机器人(Wang et al. 2018)、接触力感知(Ma D et al. 2019)等人机交互场景开展动力学研究.最近, 本文第一作者等提出了骨骼肌多柔体动力学建模新方法, 同时考虑骨骼肌质量分布、主/被动肌力、肌肉与骨骼相互作用, 应用在膝关节与脊柱运动分析(Guo J et al. 2020a, 2020b,2021a). 2021 年5 月, 由国家自然科学基金委员会数理科学部、中国力学学会生物力学专业委员会、中国体育科学学会运动生物力学分会联合举办的 “首届运动生物力学与体育科技促进研讨会”在首都体育学院召开, 本文第一作者在会上做了“人体肌骨系统柔性多体动力学建模与应用研究”邀请报告.

综上所述, 通过研究人体肌骨系统多体动力学建模、计算与实验新方法, 可揭示人体运动过程中的生物力学机制、为提高运动能力、避免损伤、加快治疗与康复进程以及研制新康复医疗设备提供计算机模拟工具. 近年来, 随着国家重点研发计划“科技冬奥”专项的实施, 越来越多的国内学者展开了人体动力学研究. 本文主要回顾了多柔体系统动力学与运动生物力学在人体肌骨系统领域的交叉研究进展, 介绍了人体运动系统基础解剖学与生物力学、神经与肌肉控制理论、肌骨系统动力学建模原理与计算方法, 以及近年来肌骨模型在多学科领域的典型应用. 最后, 作者结合前期研究经验, 归纳出人体肌骨系统多体动力学建模理论与方法领域的未来研究趋势, 为我国相关领域力学科研人员提供借鉴.

2 骨骼肌生物力学

骨骼肌具有驱动人体运动并维持其稳定的生物力学功能. 因此, 骨骼肌生物力学一直是人体动力学最具特色、最富挑战的研究主题. 人体具有至少650 块骨骼肌, 其重量超过全身体重的40% (Schweitzer et al. 2015). 如图3 所示, 骨骼肌包含肌腹与肌腱两部分, 两者均具有多级结构,可视为生物纤维复合材料(Huijing 1999). 肌腹被肌束膜分割成多个独立腔室, 每个腔室均被肌束填充. 肌束由肌纤维平行排列构成, 单根肌纤维呈圆柱状, 其直径为10 ～ 100 μm, 长度范围为1 ～50 cm (Neumann 2016). 在显微镜下, 肌束呈明暗相间的横纹(Wang et al. 1993), 内部包含粗肌丝与细肌丝. 其中, 粗肌丝代表肌球蛋白, 呈暗带, 其长度 (约1.5 μm) 几乎不随肌肉收缩而变化; 细肌丝代表肌动蛋白, 呈明带, 其变形在肌肉收缩过程中占主导, 通过肌联蛋白固定在具有Zig-Zag 形貌的肌间线蛋白. 由粗、细肌丝与肌间线蛋白构成的最小重复单元称之为肌小节 (sarcomere) , 是骨骼肌产生肌力的基本结构单元.

2.1 骨骼肌主、被动力模型

骨骼肌受运动神经元控制, 其在神经刺激下无需宏观变形即能产生主动肌力. 同时, 肌纤维间的结缔组织以及肌腱具有被动刚度, 在关节运动到一定程度时产生被动肌力, 避免关节运动超过其生理活动范围. 骨骼肌缠绕包裹在骨骼外部, 骨骼会通过肌肉与骨骼接触影响肌肉空间路径, 进而改变肌肉力臂长度与关节力矩. 此外, 骨骼肌的肌腹与肌腱串联, 肌腱非线性弹性会显著影响关节刚度.

在生理学中, 将肌小节在神经刺激下产生主动肌力的过程称之为横桥周期 (cross-bridge cycle) . 横桥是指肌球蛋白上具有球头状几何的蛋白质结构(Fitts 2008). 根据Huxley (1954)建立的肌丝滑移理论, 横桥会在神经刺激下与肌动蛋白位点结合, 通过扭动球头拖动肌动蛋白. 随后,ATP 水解释放能量, 使肌动蛋白与肌球蛋白解离, 回到横桥周期开始状态.

在建立骨骼肌力学模型时, 通常并不关注横桥周期的生物化学机制, 而是基于生物力学实验给出的横桥肌力随肌纤维长度、速度的变化数据建立拟合模型. 其中, 最经典且应用最广泛的模型为Hill 模型. 它最早由诺贝尔生理学奖得主、英国生理学家Hill 于1938 年提出(Hill 1938). 该模型揭示了骨骼肌受强直刺激时, 肌力Fmus与 肌纤维收缩速度l˙mus存在双曲关系

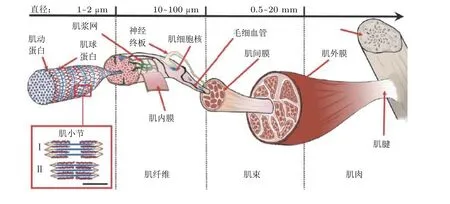
图3骨骼肌多级结构(Gotti et al. 2020)

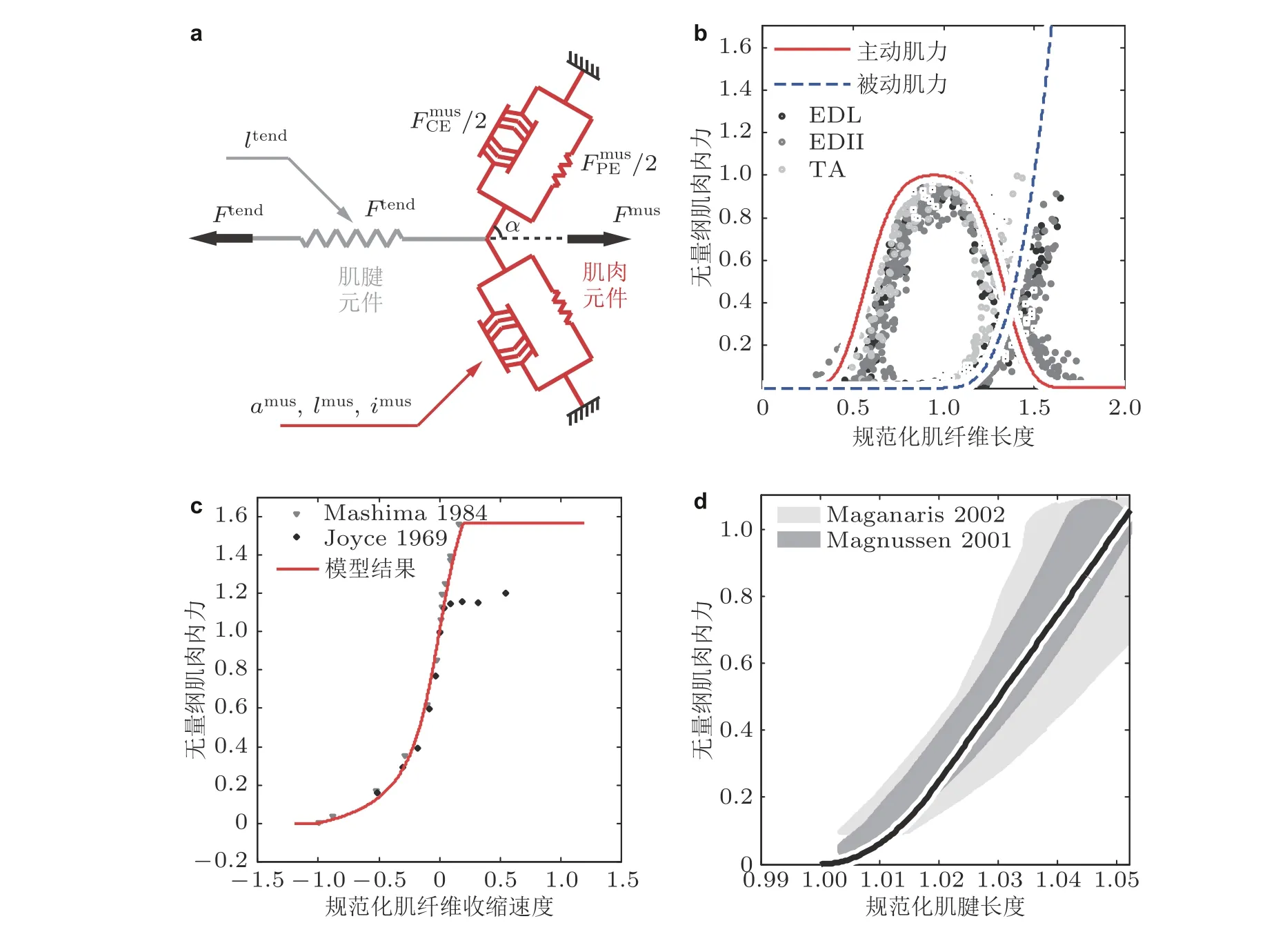
图4骨骼肌Hill-Zajac 模型(Zajac 1989). (a) 对称双羽状肌模型(Guo J et al. 2020b), 包括主动收缩元、被动弹性元与串联弹性元; (b) 主动与被动肌力随肌纤维长度变化曲线(Silva & Ambrósio 2003, Guo J et al. 2020a)及其与趾长伸肌 (EDL, EDII) , 胫骨前肌 (TA) 实验比较(Gollapudi &Lin 2009, Winters et al. 2011); (c) 主动肌力随肌纤维收缩速度变化曲线及其与生理学实验(Joyce et al. 1969, Mashima 1984)比较; (d) 肌腱串联弹性元肌力随肌纤维长度变化曲线(Blankevoort et al. 1991)及其与生理学实验 (Magnusson et al. 2001, Maganaris & Paul 2002)比较

从20 世纪80 年代末至今, Hill-Zajac 模型已被广泛应用于肌骨模型建模中. 然而, 该模型只能拟合骨骼肌整体力学功能, 无法对横桥周期的生物化学过程做定量表征, 同时忽略了肌联蛋白的生理作用. 为解决这一问题, 近年来人们根据骨骼肌的微纳米结构, 提出一系列力-生化耦合建模方法. 例如, Stoecker 等(2009)从半肌小节的力学功能出发, 建立了Huxley 形式(Huxley 1957)偏微分方程组. 为了描述肌肉刺激后出现的刚化现象, Rode 等(2009)将肌联蛋白抽象成黏性弹簧修正Hill 模型, 进一步提出三维本构(Heidlauf et al. 2016). Givli 和Bhattacharya (2009)引入肌纤维长度分布的统计特征, 建立了考虑肌小节长度非均匀性的粗粒化模型. Nishikawa 等(2012)根据生理实验结果提出了原纤维缠绕假设, 认为肌肉收缩时肌联蛋白与肌动蛋白会扭结在一起;LeMoyne 等(2014)在Hill 模型中引入虚拟滑轮定量建模这一现象. Meyer 等(2010)将Hill 三元素模型作为基本结构单元, 根据肌间线蛋白具有的阶梯状结构, 建立了网络模型.

Hill-Zajac 模型存在的另一突出问题是其忽略了骨骼肌的惯性分布. 一方面, 肌肉占人体超过40%的质量, 但Hill-Zajac 模型将肌肉质量集中到其缠绕的骨骼刚体上, 忽略了肌肉质量分布随人体运动的变化. Pai (2010)通过三头肌模型仿真证实, 肌肉质量分布会显著影响踝关节动力学, 并提出基于物质坐标的肌肉质量沿纤维分布建模方法(Sueda et al. 2008). Günther 等(2012)将骨骼肌质量离散成多个质点, 相邻质点之间通过Hill 模型连接. Millard 和Delp (2012)在肌腹与肌腱间引入集中质量, 避免肌肉力计算在低激活度时出现数值振荡. Han 等(2015)提出了考虑肌肉质量分布与截面变化的平面模型, 但其模型中忽略了主、被动力. 最近, 本文作者团队基于多柔体动力学方法, 将任意Lagrangian-Eulerian (ALE) 描述的柔性索有限单元与Hill-Zajac 模型结合, 建立了考虑惯性分布变化的骨骼肌准一维有限单元(Guo et al. 2020b). 该单元能应用于骨骼肌弹性波传递仿真, 为骨骼肌超声弹性成像原理及应用(Li & Cao 2017)提供了动力学分析工具.

此外, Hill-Zajac 模型只考虑主动肌力随肌纤维收缩速度的变化, 忽略了肌肉内部软组织具有的黏性阻尼特性. Günther 等(2007)通过数值仿真发现, 忽略上述阻尼效应会导致肌肉内力出现非物理的高频振荡, 而这种非物理高频项来源于Hill 本构关系的非线性. 为解决这一问题, Millard 等(2013)建立黏性骨骼肌模型, 引入线性阻尼器与主动收缩元件并联. 而Günther 等(2007)与Haeufle 等(2014)则通过数值仿真说明, 线性阻尼器应与Hill 主动收缩元串联才能避免非物理振荡的出现.

值得指出的是: Hill-Zajac 模型本质上是一维模型, 一般需引入等厚度假设使控制方程封闭.然而, 研究表明该方法无法刻画肌肉收缩过程中的体积不变性(Baskin & Paolini 1967). 根据Azizi 等(2008)在动物实验的测量结果, 等张收缩条件下肌肉厚度变化可超过20%. 为了在Hill 模型中引入体积效应, 李永胜与陈维毅(2007)将肌腹体积抽象成平行四边形, 提出体积相关力约束四边形面积即肌腹体积不变. Siebert 等(2014, 2016, 2017)假设肌肉受垂直横截面方向外力作用下, 垂向压力与纤维收缩内力间具有某一杠杆关系, 但其模型无法直接表征肌肉体积守恒. Randhawa 和Wakeling (2015)引入腱鞘刚度, 建立肌肉体积守恒的二维与三维模型. Dick 和Wakeling (2018)进一步基于超声测量实验, 证实了这一模型能够考虑肌纤维变形的非均匀性. 最近, 本文作者团队提出了骨骼肌厚度与肌肉空间路径解耦描述方法, 能够同时刻画骨骼肌拉伸、剪切与等体积变形 (Guo et al. 2020b).

2.2 肌肉缠绕接触问题

骨骼肌与骨骼之间存在复杂的力学约束与接触关系. 骨骼肌通过附着点与骨骼联结, 同时其缠绕在骨骼几何表面, 骨骼几何与肌肉厚度决定了肌肉力臂. 骨骼肌各横截面中心连成的轨迹称为肌肉路径(An et al. 1981), 其长度lmus对关节角度θ的 偏导数定义为肌肉力臂, 即rmus=∂lmus/∂θ(Zatsiorsky & Prilutsky 2012). 如图5(a)所示, Inman (1947)最早将肌肉路径简化为起止点连线,但这一描述过分忽略了骨骼形貌的复杂性, 导致计算得到的肌肉力臂偏差太大.

为了考虑肌肉缠绕 (muscle wrapping) , Delp 等(1990)提出了“通过点” (via-point) 约束. 如图5(a)所示, 他们认为肌肉路径在关节运动过程中始终通过确定的解剖标记点, 从而将肌肉路径简化成多段线段. 该方法简单方便, 目前仍被众多肌骨模型使用(例如:Guo J et al. 2020a). 然而, 通过点约束忽略了在某些关节角度下肌肉与骨骼脱离接触的“动态缠绕”情况, 例如股四头肌在膝关节屈曲到一定角度时, 才会与股骨髁接触. 为解决这一问题, 学者们提出了动态通过点约束(Suderman & Vasavada 2012), 即通过点约束只在关节角度满足一定范围时才起效. 但这一约束会导致肌肉路径长度随关节角度变化曲线不光滑, 得到的肌肉力臂在临界关节角度处发生奇异.

为了保持动态缠绕时肌肉路径长度连续, Garner 和Pandy(2003)提出了“障碍设置”(obstacle-set) 法, 参见图5(b). 假设肌肉路径始终保持与某一几何体接触, 根据骨骼形貌差异, 将缠绕几何形状设为椭球、圆柱、圆锥等, 肌肉路径的接触点在缠绕几何体面内运动. 最近, Hammer 等(2019)提出了多椭圆面几何缠绕, 并在多关节肌实现应用. 然而, 缠绕几何体选择及其参数需根据骨骼影像与解剖经验确定, 具有很大随意性. 根据Suderman 等(2012)与Arjmand 等(2006)研究成果, 假设的缠绕几何体参数对关节载荷与肌肉内力影响无法忽略. 为了解决这一问题, Desailly 等(2010)基于骨骼几何给出凸包, 将肌肉路径简化为凸包内的最短路径, 可根据计算几何方法快速确定肌肉路径长度. Scholz 等(2016)根据曲面微分几何, 提出了基于测地线的肌肉缠绕约束, 实现了肌肉轴线与真实骨骼几何缠绕, 但该研究无法考虑肌肉厚度的影响.

值得注意的是, 无论是采用通过点约束还是障碍设置法, 肌肉路径均由其接触缠绕的骨骼形貌确定. 因此, 如何重构三维刚性骨骼形貌已成为近年来研究者关注的重点. 大多数情况下, 研究者以标准人骨骼几何数据库作为参考模板进行线性放缩, 获取目标对象的特异性骨骼信息(Delp et al. 2007, Lund et al. 2015). Anderson 等(1999)基于受试者站立位或步态的红外标记点轨迹提取受试者体段棍图(Lund et al. 2015), 进一步通过优化方法(Andersen et al. 2010)实现标准骨骼几何模型与棍图配准. 这一方法实现较为简单, 但其忽略了儿童、性别、疾病等对受试者骨骼形貌的特异性影响. 针对这类人群, 可通过采集的CT 或核磁等医学影像重建骨骼几何(梅齐昌等2020). 这一方法能够获得毫米级精度的骨骼几何信息, 但CT 测量可能给受试者带来一定剂量辐射, 医学影像设备也很难推广到大样本肌骨系统建模当中. 统计形状模型 (statistical shape model, SSM) 能够将标准骨骼数据库的几何信息通过非线性变换与受试者匹配, 其本质是基于已获取的人群骨骼形貌, 提取主要的点云变换特征(Lamecker et al. 2016), 详见Sarkalkan 等(2014)的相关综述. 目前, SSM 已应用到下肢(Zhang et al. 2016)、髋关节(Bahl et al. 2019)、肩关节(Huang et al. 2021)的骨骼与关节形貌建模中. 最近, Suwarganda 等(2019)尝试将SSM 模型与影像学测量结合, 在确保骨骼刚体模型精度的同时降低人体辐射量; Bakke 和Besier (2020)进一步证实SSM 模型能够提高逆运动学计算的精度. 上述方法获得的骨骼均为真实的接触几何, 但骨骼三维曲面过于复杂, 导致肌肉与骨骼接触计算的效率很低(Favre et al. 2010). 因此, 如何根据重构的真实骨骼形貌, 参照医学影像信息自动拟合缠绕几何体参数(Aurbach et al.2020, Killen et al. 2021), 仍是肌骨建模需要解决的问题.

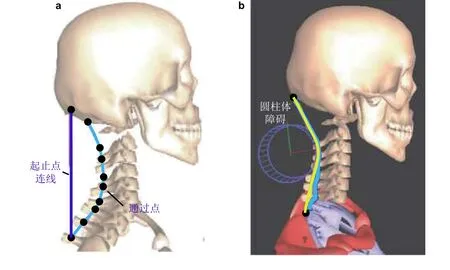
图5肌肉与骨骼缠绕描述. (a) 起止点简单连线及通过点约束(Suderman & Vasavada 2012), (b)简单几何体障碍设置(Suderman et al. 2012)

值得指出, 上述肌骨接触缠绕描述方法均将骨骼肌简化成无质量的线, 忽略了其在骨骼上缠绕产生的惯性效应. Favre 等(2010)将有限元法中的接触算法推广到肌肉与骨骼缠绕问题研究.他们采用弯曲刚度极低的梁单元对肌肉建模, 提出了基于接触检测的缠绕算法. 该方法可应用于任意骨骼曲面, 但其计算效率远低于通过点与障碍设置法. Fu 等(2019)针对机械系统提出考虑绳索质量分布的绳索单元-凸轮缠绕约束建模方法, 将有限元接触问题变为约束问题, 该方法可拓展到骨骼肌建模, 实现有限元与障碍设置法的融合. 为了提高肌肉与骨骼接触检测效率,Lloyd 等(2021)将符号向量场引入检测算法, 实现了肌肉与骨骼接触的准实时仿真, 但其研究忽略了肌肉的惯性与非线性本构. Lu 和Zhou (2011)采用等几何方法, 建立了肱二头肌有限元模型,其思想可拓展到具有复杂形貌的骨骼与肌肉接触问题. 此外, 有限胞元法 (finite cell method) 采用少量规则胞元离散骨骼边界, 适用于具有复杂形貌的骨骼与肌肉接触问题, 目前已被应用在腰椎椎体有限元仿真中(Jomo et al. 2019), 并能与柔性骨骼肌单元紧密结合.

2.3 肌腱与韧带力学模型

肌腱是肌肉末端的坚韧结缔组织, 连接肌腹与骨骼附着点. 韧带、关节囊等在关节周围构成骨骼间连接辅助结构, 上述结缔组织与肌腱在结构、功能与力学性能上十分相似, 本质上都是肌筋膜网络的沿伸. 与肌腹 (图3) 类似, 肌腱与韧带从纳观到宏观具有6 ～ 7 级多级结构(Kastelic et al. 1978). 在宏观尺度上, 肌腱被分割成多个腔室, 每个腔室中由肌束填充; 肌束分割成多束纤维, 其基本结构单元为原纤维. 原纤维呈阶梯状排布形式, 通过交联糖蛋白相互连接. 原纤维的“砖块”是微纤维, 微纤维内部由胶原分子构成. 在纳米尺度上, 微纤维的空间结构与原纤维十分类似, 即胶原分子极性使其按阶梯状排布, 相邻阶梯的分子间会形成扭结. 因此, 韧带与肌腱的多尺度空间结构具有显著的自相似特征(Puxkandl et al. 2002, Gautieri et al. 2011).

在建立肌骨模型时, 一般只考虑肌腱与韧带沿主轴方向拉伸的非线性弹性性质, 其中最常见的函数形式由Blankevoor 和Huiskes (1991)提出, 参见图4(d). 胶原纤维在无外力作用下呈卷曲状态(Weiss 和 Gardiner 2001), 而构成同一阶梯的不同胶原纤维呈螺旋状排布(Gautieri et al.2011, Shearer 2015). 在外力作用下, 卷曲的胶原纤维首先伸直来承受外力, 导致肌腱力-变形曲线存在非线性趾区 (toe region) . 胶原纤维伸直后, 肌腱轴向变形主要为纤维间螺旋的螺距增大, 此时其变形机制与线性弹簧十分类似. 在宏观上, 肌腱力-变形曲线表现为线性.

为了将肌腱/韧带的拉伸性能与其多空间尺度结构之间建立关联, Freed 和Doehring(2005)基于原纤维扫描电镜结果, 建立了肌腱/韧带非线性拉伸本构, 但其忽略了胶原纤维螺旋的结构变化. Reese 等(2010)同时考虑了胶原纤维与肌束的多级螺旋结构, 兼顾肌腱拉伸非线性与大泊松比特性. Thorpe 等(2015)与Shearer 等(2017)进一步证实, 胶原纤维构成的螺旋是肌腱储存弹性势能的基本结构. Szczesny 和Elliott (2014)基于微纳米实验, 揭示了原纤维之间剪切是肌腱/韧带重要的内力传递机制. 更进一步, Ahmadzadeh 等(2015)将Ji 与Gao (2004)提出的拉剪理论应用于原纤维自相似结构, 建立了原纤维多孔介质模型.

除与时间无关的非线性弹性之外, 肌腱与韧带还具有显著的黏弹性特征, 而其微纳尺度自相似空间结构决定了宏观黏弹性响应的长时程性(Gupta et al. 2010, Gautieri et al. 2012b). 对黏弹性生物材料建模, 一般采用Fung (1993)提出的准线性黏弹性本构, 引入短、长两特征时间参数刻画蠕变与松弛响应. 但Doehring 等(2005) 发现, 长时程弛豫时间难以确定, 多数情况下需引入Prony 级数才能较好地拟合实验结果(Troyer 和 Puttlitz 2012). 另外, 准线性黏弹性模型在物理上对应线性弹簧与阻尼器构成的“标准线性固体”(Fung 1993)相互串联, 得到的弹簧-阻尼模型与生物材料的空间结构特征没有关联.

研究上述问题的另一思路是继承Fung 模型基本思想, 通过线性弹簧与阻尼器的串并联组合反映黏弹性特征, 但此时弹簧-阻尼器元件的组装方式抽象自肌腱/韧带多空间尺度结构. Gautieri 等基于原子力显微镜观测(Gautieri et al. 2011)、分子动力学仿真(Gautieri et al. 2012a)等手段探究肌腱的结构自相似性与响应长时程性的内在关联, 并提出具有阶梯拓扑的弹簧-阻尼器网络(Gautieri et al. 2012b, 2013). 然而, Ghodsi 和Darvish (2016)通过分子动力学模拟指出, 胶原纤维弛豫时间相比原纤维松弛行为差8 ～ 9 个数量级, 似乎难以只基于原纤维力学行为去预测宏观尺度力学响应. 为了解决这一问题, Gupta 等(2010)提出了包含纳观胶原纤维与微观原纤维响应的跨尺度黏弹性模型, 但其黏弹性元件忽略了每一级结构的自相似特征. 最近, 本文第一作者受Blumen 和Schiessel (1993)建立的阶梯黏弹性模型启发, 从肌束与原纤维共同具有的阶梯状自相似结构出发, 抽象出具有阶梯状拓扑的胞元模型(Guo J et al. 2019). 该阶梯胞元模型能够很好地拟合脊柱与膝关节韧带松弛响应(Guo J et al. 2019), 同时成功地刻画了肌腱从纳米尺度到宏观的多尺度黏弹性行为(Guo et al. 2021c).

2.4 肌筋膜力学模型

如图3 所示, 肌筋膜 (fascia) 系统包括包覆肌腹的肌外膜、分割肌束的肌束膜、肌纤维间的肌内膜以及神经血管束(Adstrum et al. 2017). 肌筋膜曾是被人们“忽略”的结缔组织, 直到近20 年, 其在骨骼肌内力传递的重要作用(Huijing 2007, 2009; Purslow 2010)才逐渐被认识. 学者们通过大量动物解剖(Maas et al. 2001)实验, 证实肌筋膜能够在肌肉内部(Yucesoy et al. 2003)与肌肉间(Yucesoy et al. 2005)传递内力. Huijing 等(2011)通过核磁影像发现, 肌外膜牵拉会导致小腿三头肌非均匀变形, 同时证实肌肉功能的协同性 (参见3.3 节) 一部分来自于肌外膜联络(Maas & Huijing 2009). Carvalhais 等(2013)通过髋关节等速加载实验, 证实背阔肌与臀大肌间存在筋膜连接.

肌筋膜特别是肌外膜, 将不同肌肉连接成统一整体. 在对肌骨模型的大多数研究中, 将骨骼肌视为独立的力元, 忽略了广泛存在的结缔组织联系. Yucesoy 等(2008)通过有限元仿真, 分析了肌外膜改变鼠腓肠肌内力传递的机制, 但其研究难以推广到大尺度肌骨系统. Bernabei 等(2016)在Hill 肌肉模型的基础上, 将肌筋膜建模为弹簧元件, 分析了肌筋膜对小腿三头肌内力传递的调制作用. 本文作者团队提出滑动铰模型(Guo et al. 2020b), 实现被肌外膜间隔的腓肠肌内、外侧头总质量守恒. 考虑肌筋膜连接的滑动铰模型, 提高了小腿三头肌实测拉伸弹性与仿真内力之间的相关性, 相关系数范围与尸体实验结果(Maïsetti et al. 2012)一致.

3 神经与肌肉控制理论

3.1 骨骼肌兴奋收缩耦合方程

骨骼肌被运动神经元支配, 其激活过程被称为兴奋收缩耦合, 分为以膜电位变化为特征的兴奋与肌小节收缩 (2.1 节) 两大过程. 兴奋收缩耦合首先由神经系统产生兴奋电信号, 通过神经终板传递到骨骼肌. 兴奋电位从细胞体传递到神经终板的过程存在时间延迟, 描述兴奋电位传递可采用光滑索模型(Baer & Rinzel 1991). 然而, 神经纤维表面并非光滑, 而是分布着一类称为棘突的伞状突起, 而棘突分布会改变神经元的时间尺度(Zador et al. 1995). 例如, Santamaria 等(2006)的实验表明, 棘突会困住在神经元胞质中自由扩散的钾、钠离子, 影响神经兴奋传递. 为反映神经元结构对其功能的影响, Mainen 和Sejnowski (1996)在胞体与树突之间引入耦合电阻, 但该电阻缺乏明确的神经元结构对应. Van Ooyen 等(2010)进一步在神经索模型中引入树突, 讨论其对神经冲动发放率的影响. 最近, 本文第一作者从神经元功能电路模型抽象出具有自相似结构的电学胞元, 发现棘突会改变分形功能电路的拓扑结构, 进而影响兴奋电位传递的特征时间(Guo et al. 2020c).

目前, 绝大多数肌骨模型使用常微分方程来描述兴奋收缩耦合(Winters 1995). 该模型假设不同肌束的兴奋电位能够线性叠加, 得到光滑的神经刺激信号u. 以Thelen (2003)提出的一阶非线性模型为例, 肌肉激活度a与 神经刺激u之间满足

此处,τact与τdeact分别为刺激时间和解刺激时间. 其他典型的兴奋收缩耦合模型还包括Zajac(1989), Pandy 等(1990), Raasch 等(1997)提出的形式. 最近, 随着高密度EMG (Moya-Esteban et al. 2020)的逐步推广, 学者们尝试在兴奋收缩耦合方程中引入单一神经元产生兴奋的生物学过程(王如彬等 2020). 例如, Sreenivasa 等(2016)采用带泄漏整合发放模型 (leaky integrate-andfire, LIF) 模型描述单一神经兴奋, 在此基础上建立神经网络, 打破了线性叠加假设. 但迄今为止,尚无成熟的肌肉兴奋收缩耦合模型能完全刻画神经产生兴奋电位的电生理过程.

3.2 肌肉最优控制

3.2.1 静态优化

人体骨骼肌控制具有冗余性, 即关节的单自由度运动同时受多条肌肉控制. 例如, 股四头肌群中, 股直肌、股外侧肌、股内侧肌、股中间肌激活均能实现膝关节伸展. 在数学上, 肌肉冗余性意味着动力学方程数目少于独立的肌束数目.

为了分配各肌束的肌力, Delp 等(1990)提出静态优化 (static optimization) 算法. 目前, 静态优化是肌骨动力学分析最简单, 最常用的肌力分配算法. 静态优化的核心是引入时间无关性假设, 即认为骨骼肌内力分配只与当前时刻的人体动力学状态量有关, 与人体运动的时间历程无关(Quental et al. 2016). 在该前提下, 描述人体各个骨性刚体运动的广义坐标q、广义速度q˙与广义加速度q¨均可通过实验测定, 即人体的运动惯性力已知, 从而将描述动力学问题的微分-代数方程组简化为以激活度矢量a为自变量的代数方程组. 由此对应的数学模型可写作如下形式

其中, 静态优化的目标函数J常写作第i(1 ≤i≤Nmus)束 肌肉激活度ai的p次幂加权和形式(Ackermann & van den Bogert 2010), 权重wi可取单位1 或肌肉体积、生理截面积等生理学参数. 此处,激活度的线性和 (p=1)对 应肢体末端刚度(Pham et al. 2014), 平方和 (p=2)与肌肉做功相关(Thelen & Anderson 2006), 立方和 (p=3)可视为肌肉疲劳的度量(Ackermann & van den Bogert 2010). 此外, 在Anybody 软件的肌骨模型中, 常采用min-max 目标函数, 即p→∞(Rasmussen et al.2001). 因此, 如何在上述目标函数中选择适合人体运动的形式, 成为困扰静态优化仿真研究的一个难题. Bottasso 等(2006)提出根据实验数据推测优化函数形式的方法, Ackermann 和van den Bogert (2010)针对目标函数对肌骨模型仿真结果的影响做系统讨论. 最近, Wochner 等(2020)提出了基于机器学习中贝叶斯优化确定目标函数的方法.

在式(5)中, 广义力Qjoint一般根据只考虑人体节段的动力学方程确定, 在某些特定工况下亦可通过等速测力计(Huang et al. 2017)、手持式测力仪(Hegarty et al. 2019)等实验装置测定. 关节角度对应的Qjoint代 表广义力矩, 相应的Rmus矩 阵元素为关节力臂.Qext表示重力、地面反力、人机交互力等其他外力作用. 通过运动捕捉或惯性传感器, 可获取人体肌骨系统空间位形(q,q˙)与 广义加速度q¨ , 作为运动学输入代入动力学方程. 对于人体质量与惯量分布矩阵M, 一般可根据人体形态学测量给出的归一化表格(Winter 2009), 通过测量受试者身高与体重确定, 肌肉质量假设附着在骨骼刚体上. Ayusawa 等(2011)提出了人体各个环节质量的快速辨识方法, Hayashibe 等(2011)进一步提出了肌肉质量分布的辨识方程.Cq为 人体关节约束方程C对广义坐标q的Jacobi,λ为约束力矢量. 根据式(3)可知, 肌肉力矢量Fmus与 激活度矢量amus间满足线性关系,整理后可得静态优化模型的线性约束方程. 此外, Dickerson 等(2007)与Akhavanfar 等(2019)分别提出了考虑肩关节与脊柱稳定性的不等式约束, 在满足动平衡方程的基础上引入稳定性限制.

静态优化假设将描述动力学问题的微分代数方程组求解问题转化为优化问题, 大幅降低了求解难度与计算代价. 然而, 绝大多数静态优化模型所预测的肌肉激活度与实测EMG 仅具有定性相关性, 在数值上存在显著差异(Kian et al. 2019). 另外, 式(5)中的动平衡方程约束需假设肌腱为刚体, 某些复杂肌骨模型(例如: Ignasiak et al. 2018, Ignasiak 2020)甚至不考虑被动弹性元件贡献, 导致无法考虑Hill 模型中的全部力元(Pizzolato et al. 2015). 为了解决此问题, Thelen 和Anderson (2006)提出计算肌肉控制 (computed muscle control, CMC) 方法, 在离散时间点处基于静态优化确定肌肉激活度, 在时间积分步导入正向动力学模型来修正轨迹误差, 但该方法会导致计算量显著增加. Shourijeh 等(2016)将关节力矩引入优化目标函数, 放松动平衡方程, 提出了“正向肌肉-逆向骨骼”的混合优化方法, 从而计入Hill 模型中的三类元件, 并引入了兴奋收缩耦合方程.

为了改善静态优化计算结果, 可采用生理采集信号对其进行修正. 近年来, 结合EMG 信号的肌骨系统逆向优化算法以成为研究热点. EMG 是电极覆盖的肌纤维生物电信号的叠加, 在一定程度上能反映肌肉活动(丁其川等 2016). 相比针刺电极、贴附在皮肤表面的表面肌电 (surface electromyography, sEMG) 具有非侵入、实现简单等特点, 在肌骨系统建模中得到了广泛应用. 为了将获得的EMG 信号转化成肌肉激活度曲线, 一般需对其做翻正、滤波以及归一化操作. 归一化操作一般需根据最大等长收缩测试(maximal voluntary contraction, MVC)实现(Bamman et al. 1997), 但传统的徒手测量操作对测试者提出了较高要求, 而替代徒手操作的等速加载仪器难以实现便携化, 另外患者、运动员等特定人群无法完成某些MVC 动作. 因此, 研究者提出了基于人体环节重量(Nishijima et al. 2010), 多个非MVC 动作插值(Marras et al. 2001), 以及冲刺跑等爆发力动作(Albertus-Kajee et al. 2010)测量骨骼肌MVC 的实验方案.

2003 年, Lloyd 和Besier (2003)建立了基于EMG 驱动的膝关节模型, 根据实际测量获取关节运动, 将归一化EMG 信号作为神经与肌肉刺激, 逆向求解肌肉力(Buchanan et al. 2005). 李翰君等(2014a)将EMG 驱动与逆向动力学相结合, 通过最小化正、逆向求解力矩误差求解最优肌纤维长度. 由于人们只能测量近皮肤表面肌肉的EMG, 对于股内侧肌、比目鱼肌等深层肌群的激活度只能通过其他表面肌肉线性加权. 后来, 人们提出EMG 辅助肌骨系统逆向优化, 即令测量EMG 的肌群根据实测信号确定其肌力, 其他骨骼肌的激活度通过逆向优化得到. 进一步, Sartori 等(2014)放松表面肌群激活度与EMG 的约束关系, 提出同时考虑深层肌肉激活度、关节力矩与EMG 误差的加权目标函数. Pizzolato 等(2015)开发了开源程序包CEINMS, 其中集成了不同的EMG 辅助优化算法. Durandau 等(2018)提出了基于EMG 测量的肌骨系统快速在线仿真算法, 为肌骨模型仿真与可穿戴设备准实时交互提供可能.

3.2.2 动态优化

静态优化忽略了人体肌骨系统的时间效应, 导致基于静态优化得到的肌肉激活度, 无法驱动同一肌骨模型复现实测运动. 为了使肌骨系统仿真结果严格满足动力学方程, 学者们提出了动态优化 (global optimization) 方法. 该方法与静态优化在同一时期诞生, 例如Davy 和Audu (1987)提出了综合轨迹跟踪误差与生物能 (metabolic cost) 的目标函数, 计算步态摆动期的下肢肌肉发力. Pandy 等(1990)基于一平面肌骨模型, 以人体质心高度最高为优化目标, 确定了跳高过程的肌肉激活度. 随后, Anderson 和Pandy (1999)将二维肌骨模型拓展至三维, 基于同一优化目标正向分析跳高过程. 该分析方法被进一步拓展至步态(Anderson & Pandy 2001a), 以生物能消耗为优化目标, 通过正向仿真确定全步态周期的肌肉激活度. Anderson 和 Pandy (2001b)进一步将这一方法与静态优化计算结果进行系统比较, 证实二者在临床上等价.

动态优化方法放弃式(5)中的动平衡方程约束, 对肌骨多柔体系统动力学方程直接积分. 在积分前确定各肌肉激活度随时间变化, 完成一组仿真后根据目标函数J的变化梯度再调整激活度曲线. 因此, 动态优化模型的数学形式可总结如下

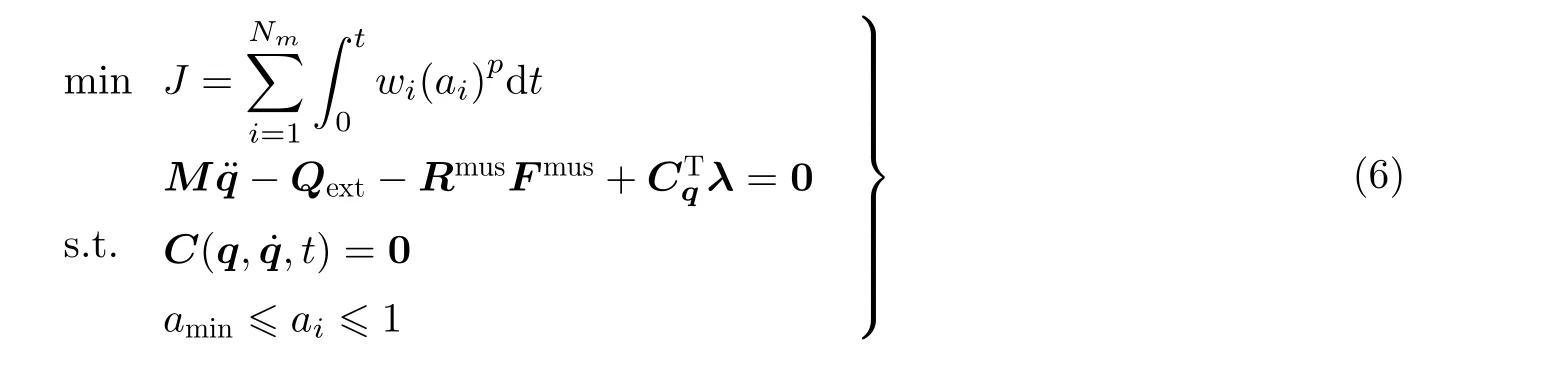
与静态优化方法相比, 动态优化的计算量巨大, 因为其优化迭代过程需要多次求解动力学方程. 为解决该问题, 近年来学者们提出一系列方法加速动态优化. 例如, De Groote 等(2009)通过变量替换方法, 将非线性动态优化转换成凸优化问题. Shourijeh 等(2014)采用Fourier 级数拟合激活度曲线, 降低了优化自变量数目. Quental 等(2015)提出了滑窗动态优化方法, 将全域时间积分退化为滑窗内时间积分. De Groote 等(2016)将直接配点法引入动态优化模型, 这一思想已被应用在开发OpenSim-Moco 肌骨动力学优化控制程序(Dembia et al. 2020). Rahmati 等(2017)提出变量代换法, 使各肌肉的激活度始终满足动力学方程, 将有约束优化问题转化为无约束优化.Shourijeh 等(2017)在每一时间步做无约束动态优化, 进一步通过有约束局部优化修正肌肉激活度.

3.3 肌肉协同控制

在肌骨系统建模中, 往往假设不同肌束间相互独立. 然而, 实验结果(Cheung et al. 2012, Hirashima & Oya 2016)表明, 在某些运动条件下, 不同肌束的激活度高度相关(Pan et al. 2018), 而神经系统疾病可能改变这种相关性. 这种相互依赖的神经-肌肉控制模式被称为肌肉协同性(muscle synergies) . Bernstein (1966)最早指出肌肉协同性问题, 认为人体通过将特定的协同模式储存在神经回路中, 可减少人体运动的冗余自由度(杨毅et al. 2020). 大多数研究认为, 肌肉协同性是源自于大脑或脊髓(Tresch & Jarc 2009), 但Kutch 和Valero-Cuevas (2012)基于尸体实验对上述观点提出质疑, 并进一步通过肌骨模型仿真(Valero-Cuevas et al. 2015)说明, 肌肉协同模式来自人体动力学与目标运动特征.

肌肉协同模式可由多通道EMG 信号A(t)提取, 其中在肌骨动力学中应用最为广泛的是时不变协同模型(Chiovetto et al. 2013). 如图6 所示, 该模型将A(t)分解成反映空间特征的协同结构矩阵WNmus×Nsyn与 时间相关的矢量H(t), 即

这一模型将肌骨系统中独立的控制变量数目从肌束个数Nmus降 至协同模式数目Nsyn,error为提取Nsyn阶协同模式后剩余的非线性组分, 一般根据其范数判断是否需进一步提取协同模式. 时不变协同结构矩阵W可通过非负矩阵分解(Févotte & Idier 2011)、主成分分析(Tresch et al. 2006)等方法提取. Cheng 等(2019)在H(t)中引入时间延迟, 提高了协同模式提取的鲁棒性.

近年来, 肌肉协同模式被广泛地引入肌骨系统优化控制建模中, 在考虑个性化神经与肌肉控制特征的同时降低控制变量数目. De Groote 等(2014)证实, 肌肉协同模式可视为神经与肌肉优化控制受运动目标约束下的独立控制变量. Walter 等(2014)发现, 考虑协同性的肌骨系统静态优化可提高膝关节接触载荷预测精度. Steele 等(2015)比较基于静态优化与直接由EMG 提取的协同激活模式差异, 认为人体动力学特征会改变协同激活模式. Razavian 等(2015a)给出了单关节肌骨模型最优控制的显式解, 求得激活模式给出的肌肉激活度受关节姿态调制. 该研究团队(Razavian et al. 2018)还进一步提出了基于协同模式的非优化控制策略, 并通过在体实验证实了基于协同模式实现神经与肌肉控制的可行性.

3.4 神经与肌肉多层级控制

在上述优化理论与协同理论中, 均忽略了人体神经与肌肉控制具有的多层级特征. 事实上,人体运动控制器是由大脑初级运动皮层、脑干、基底神经节、小脑构成的高级大脑中枢, 脊髓反射以及遍布全身的感受器构成的多层级网络结构(王瑞元等 2018). 骨骼肌运动受脊髓、脑干和大脑皮质三级调控, 小脑与基底神经节监控人体运动, 神经系统各层级各司其职, 功能上具有独立性.

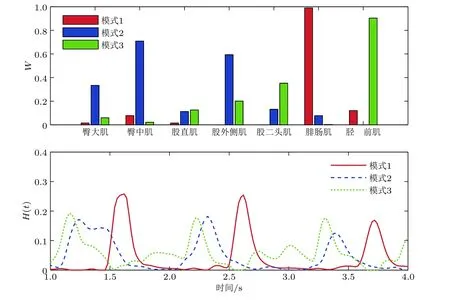
图6基于非负矩阵分解(Févotte & Idier 2011), 由健康人3 个步态周期提取的典型肌肉协同模式

迄今, 人类对神经与肌肉多层级控制的机理认识仍不深入. 近几年, 学者已开始尝试建立具有多层级特征的控制模型, 确定肌骨模型的肌肉激活度. 例如, Razavian 等(2019)将人体运动控制分成两级: 高级控制器只规划关节运动轨迹; 而低级控制器根据协同性分解各肌肉内力, 实现骨骼肌内力的快速计算. 如图7 所示, Walter 等(2021)建立了包括运动感知规划、控制信号转导、兴奋收缩变换三级控制系统, 实现了人体肌骨系统的站立与下蹲模拟. 然而, 该控制模型需要非常多的参数输入, 难以根据有限的神经生理学实验确定. 此外, Haeufle 等(2020)以手臂控制为例, 指出神经与运动控制计算量随层级提高而增大.

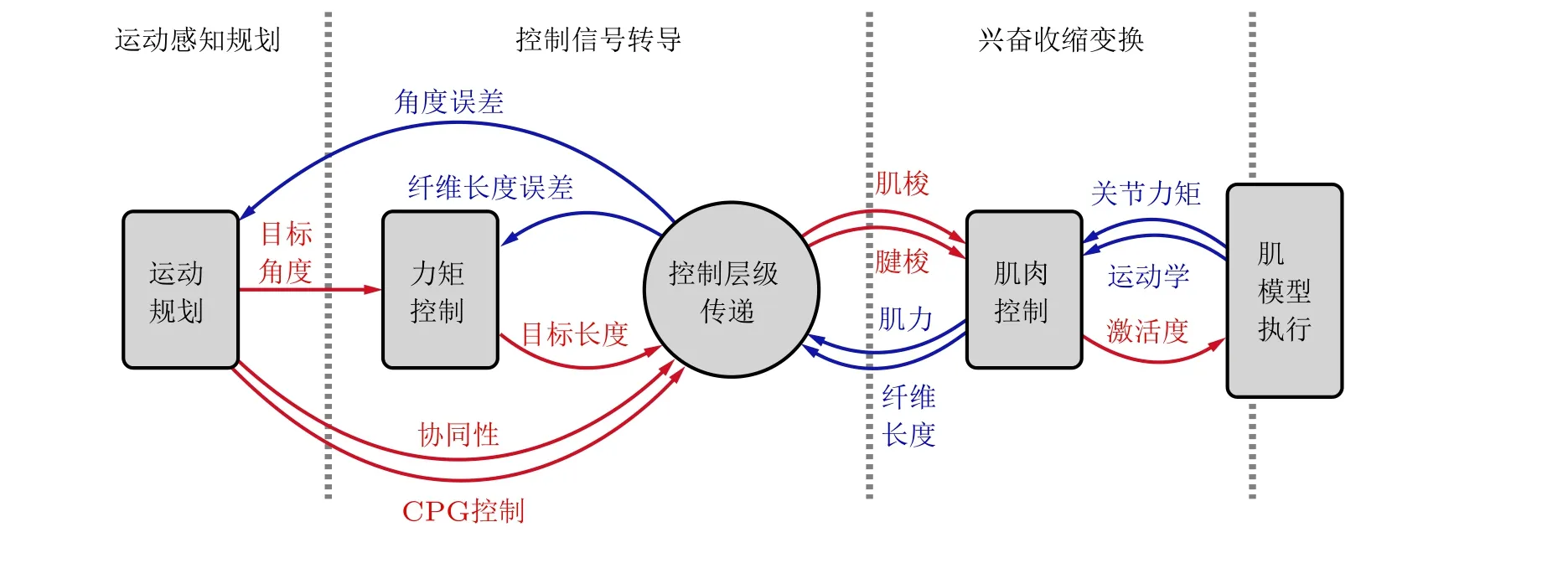
图7 Walter 等(2021)建立的多层级神经与运动控制模型.

与此同时, 学者们已对基于脊髓反射的肌骨系统控制开展了较为系统的研究. 其中, 中枢模式发生器 (central pattern generator, CPG) 理论已较为广泛地应用在人体节律运动的控制中.CPG 可自发、独立地产生周期性信号, 指挥骨骼肌产生协调重复性收缩(王树明 2018). Zhang和Zhu (2007)基于CPG 模型与人体简化动力学模型, 预测步态周期的下肢肌肉激活度. 随后, 董玮等(2008)基于下肢神经解剖特点对Zhang 和Zhu 建立的模型做进一步修正, 并拓展到上肢周期运动(吴炯等 2010)中. 然而, 该模型对足与地面接触过于简化. Razavian 等(2015b)将CPG 控制器与手臂肌骨模型结合, 实现屈肘动作的正向仿真, 但其难以拓展到更大尺度肌骨系统建模.

另一种典型的脊髓反射称之为牵张反射. 牵张反射是指肌梭感受到肌肉长度变化后, 通过γ 环改变骨骼肌激活度的控制模式(王树明 2018). 该反射的潜伏期很短, 因此对外界干扰刺激响应快速、同时不受中枢神经直接调制. 利用这一原理, Zhang C 等(2019a, 2019b)将肌骨模型与牵张反射结合, 模拟脊柱受振动载荷条件下的动态响应. Geyer 等(2010)以牵张反射作为平面步态模型的基础控制器之一, 实现了平面人体肌骨模型的正向行走仿真. 除肌梭之外, 肌腱内还分布着一类张力感受器, 称之为腱器官或腱梭. Mileusnic 等(2006)提出了以腱梭作为肌肉内力传感器的力学模型. Williams 等(2014)将腱梭、肌梭模型集成到静态优化控制器中, 实现了手臂刷牙动作快速仿真. Zhang H 等(2020)进一步将上述思想拓展到步态动力学仿真中, 仿真得到的肌肉激活度与EMG 测量结果一致.

4 神经肌骨系统多体动力学

4.1 控制方程求解与分析

人体神经肌骨系统的控制方程包括两部分, 即肌骨多体系统动力学方程与兴奋激活耦合方程, 可写作如下形式(Guo J et al. 2020a)

4.1.1 逆向动力学

逆向动力学需测定受试者的关节运动学与外力信息, 将式(8)作为约束方程求解关节力矩Qjoint, 进而计算骨骼肌内力. 逆向动力学往往基于静态优化算法 (详见3.2.1 节) 求解, 解决骨骼肌内力分配的冗余性问题, 计算效率远高于正向仿真. 为了进一步实现逆向优化的准实时计算,Murai 等(2010) 将伪逆算法引入逆向优化问题求解, Moissenet 等(2012)进一步探讨了伪逆算法相比传统优化求解方法的效率提升, Razavian 等(2015a)针对单关节肌肉控制, 求出肌肉激活度的理论解与对应的协同模式.

近年来, 肌骨系统逆向动力学问题的运动学输入, 已经由传统的红外动作捕捉逐渐拓展到惯性传感器(Karatsidis et al. 2019)、Kinect 体感相机(Skals et al. 2017b)等, 这使肌骨模型应用于实验室以外场景成为可能. 近年来, 随着计算机视觉的发展, 深度学习算法(Nie et al. 2019, Sun et al. 2019)能够从多通道视频中快速提取人体21 个关键点, 并应用在体育比赛实际场景中(李翰君等 2020), 其关键点识别精度达到厘米级(刘卉 等2021). 目前, 本文作者团队已初步实现利用上述人体关键点运动学数据驱动肌骨模型, 通过在逆动力学求解中引入软组织约束, 避免髋关节出现非生理性内/外旋, 进一步推动肌骨模型在竞技体育、患者居家康复等场景的应用.

4.1.2 正向动力学

正向动力学研究能够考虑人体运动过程中的骨骼肌非线性动力学与软组织惯性效应. 这类研究一般以肌肉激活度a与 外载荷Qext作为模型输入, 求解人体各个节段与关节运动量. 由于基于优化控制的正向动力学研究会带来巨大计算量, 因此通常采用试凑法给出各个肌肉的激活度曲线(Tuijt et al. 2010, Rupp et al. 2015). 这种方法适合于小规模肌骨系统, 例如口颌(Lloyd et al.2012)、肘关节(Röhrle et al. 2017)等问题的求解, 或者是肌肉等长/等速收缩问题(Serpas et al.2002, Hume et al. 2018). 针对下肢步态模型, 可通过比例-微分-积分 (proportional-integral-derivative, PID) 控制正向驱动. 但该方法需引入给定的协同模式, 消除骨骼肌的冗余性. Navacchia 等(2019) 根据生理截面积分配同一关节的不同肌肉激活度; Razu 和Guess (2018)实现了基于EMG 与PID 协同控制的正向仿真; Khasian 等(2020)则将控制同一关节运动的多束骨骼肌合并考虑激活度.

肌骨系统的正向动力学分析能够与有限元方法深度结合. 例如, Guess 等(2010, 2015)采用有限元离散半月板, 提取下肢肌骨模型中的半月板刚度矩阵. 最近, Müller 等(2020)实现将半月板非线性有限元模型与肌骨系统正向仿真融合, 通过有限元提取关节三维接触载荷, 导入到肌骨系统仿真关节三维运动, 但其仍无法实现精细有限元模型与肌骨正向仿真强耦合. Navacchia 等(2019)与Hume 等(2019)建立了包含精细膝关节周围组织建模的肌骨模型, 基于显式动力学求解坐站转移与步态摆动期膝关节载荷, 但其计算量巨大. 为解决这一问题, Mo 等(2019)将肌骨模型正向动力学分析与三维骨骼肌精细有限元模型耦合, 并基于运动学跟踪误差调整肌肉激活度,降低了系统计算量. 然而, 精细有限元模型往往忽略了骨骼肌的惯性效应, 难以准确仿真跑步、跳跃、侧切等快速运动.

近年来, 多柔体系统动力学方法已被逐渐推广到人体肌骨系统建模 (图8) , 提出的各种模型兼顾了人体动力学特征与计算效率. 如图8(a)所示, 浮动节点坐标法被Mikkola 等应用在小变形体 (例如骨骼) 建模(Kłodowski et al. 2011a, 2016). Al Nazer 等(2008, 2011)采用模态柔性体替代刚性胫骨模型, 在LifeMOD 插件中采用正向动力学方法分析步态载荷. 随后, Kłodowski 等(2011b)将这一方法推广到股骨应变分析, 并计算了摔倒等易诱发股骨颈骨折工况的股骨三维变形(Kłodowski et al. 2012). Gervais 等(2018)建立了股骨假体的Craig-Bampton 动力学降阶模型,并与人体多刚体模型耦合. Geier 等(2019)进一步将定量CT 引入肌骨建模, 建立个性化股骨降阶模型, 并与Anybody 步态肌骨模型耦合分析.

骨骼肌、韧带等柔性组织在人体运动过程中会产生大变形, 例如在最大等长收缩条件下, 肱二头肌应变能够达到25% ～ 30% (Lopata et al. 2010). 绝对节点坐标法 (absolute nodal coordinate formulation, ANCF) 为此类大变形柔性体提供了有效的建模方法(Shabana 1997, 2011). Shabana等将ANCF 法应用到膝关节内、外侧副韧带建模(Mohamed et al. 2010, Weed et al. 2010), 并提出了韧带与骨骼附着点约束方程组(Gantoi et al. 2010). 进一步, Gantoi 等(2012, 2013)将ANCF 梁单元与薄板单元应用在关节软骨接触中, 并基于等几何描述刻画了股骨髁与胫骨平台三维形貌. 然而, 上述研究均限于只发生被动拉伸变形的结缔组织, 难以直接应用于骨骼肌主、被动肌力建模. Röhrle 等(2017)基于实体单元离散肱二头肌、肱三头肌, 建立的动力学模型考虑了骨骼肌三维几何、超弹性本构与主动肌力, 通过正向积分求解肘关节运动, 但尚未考虑骨骼肌惯性. 最近, Gfrerer 和Simeon (2021)基于连续介质力学推导, 得到考虑骨骼肌结缔组织超弹性的柔索单元, 参见图8(b), 但该方法难以推广到大尺度肌骨系统建模. 本文第一作者建立了考虑骨骼肌主、被动肌力与惯性分布的一维索单元(2020a, 2020b)与二维膜单元(Guo J et al. 2021a), 考虑了骨骼肌的惯性分布以及肌肉物质跨关节流动, 基于隐式向后差分方法求解式(8). 所建立的柔性肌肉单元模型实现了肌肉惯性, 主、被动肌力, 体积守恒, 以及纤维间结缔组织弹性的同时建模, 参见图8(c).

除了ANCF 方法之外, 几何精确梁 (geometrically exact beam formulation, GEBF) 也能有效地处理柔性体的大转动与大变形耦合问题, 近年来被广泛应用在软体机器人的动力学建模. 例如, Renda 等(2018)提出基于Cosseat 梁理论的几何精确梁模型, 在软抓手分段等曲率模型中引入剪切和扭转变形. 这一工作被拓展到仿章鱼触角绳驱软体机器人建模(Renda 2014). Grazioso等(2019)进一步通过实验验证GEBF 对软体机器人末端位移的预测精度. 目前, 几何精确梁在人体肌骨建模的应用集中在脊柱. Valentini 和Pennestrì (2011)使用三维弹性样条曲线比拟人体脊柱, 并分析头足向振动传递率(Valentini 2012). 但由于不同节段的椎间盘生物力学参数差异显著(Zanoni et al. 2020), 使脊柱梁模型整体的弹性模量难以估计. 另外, Lie 群理论已被初步应用于人体动力学建模(魏高峰等 2009), 并在人体姿态识别领域取得了很好效果(Vemulapalli et al.2014, 丁和恩 2019). Brüls 教授将几何精确梁单元与Lie 群结合, 并且公开了其部分计算程序(Brüls et al. 2012; Sonneville et al. 2014), 通过Lie 群建模原理可望实现几何精确单元与人体动力学建模的深度融合.

柔性单元的引入, 使人体肌骨模型的自由度数从多刚体假设下的几十个增至上万个. 如何提高正向动力学求解的计算效率, 是多柔体系统动力学方法在人体肌骨建模领域推广亟待解决的问题. 为提高高维DAEs 的求解效率, Li 等(2016)提出了并行递归算法, 在关节约束与单元节点处将多柔体系统拆分, 根据静力缩聚法简化每个子系统的内部自由度. Tang 等(2019)将经典Craig-Bampton 降阶技术进一步发展, 通过构建自适应模态基来描述大变形柔性体动力学行为,并推广到黏弹性多柔体系统(Tang et al. 2021). Luo 等(2017)将本征正交分解 (proper orthogonal decomposition, POD) 应用到多柔体系统, 类似思想同样能应用于人体动力学建模. 例如, Dumas等(2014a, 2014b)基于POD 方法分析跑步过程中软组织振动对红外标记点位置的影响, 并将软组织视为悬挂质量 (wobbling mass) 建立振动模型(Dumas & Jacquelin 2017). Mordhorst 等(2017)基于POD 方法, 实现了骨骼肌多通道EMG 信息的降阶分析. 另外, 基于数据驱动的代理模型, 能够实现将关节精细接触模型与全人体肌骨模型多尺度耦合, 避免局部计算步长对整体系统的影响. Lin 等(2010)基于代理模型思想, 将基于弹性基础模型(Blankevoort et al. 1991)建立的膝关节假体精细有限元模型与人体肌骨多体模型耦合. Eskinazi 和Fregly (2015a)开发了开源程序包SCMT, 实现肌骨系统与假体代理模型快速建模. 上述学者还将人工神经网络引入假体代理模型的构建中(Eskinazi & Fregly 2015b). 然而, 目前对人体肌骨系统数据驱动代理模型的研究集中在假体建模领域, 对肌肉、韧带等软组织的动力学降阶建模研究工作仍十分缺乏.

4.1.3 预测动力学与非线性分析

预测动力学 (predictive dynamics) 可视为一类特殊的正向动力学算法, 其基本原理参见Xiang 等(2010)的综述. 与其他两类问题相比, 仿真时描述人体关节运动的广义坐标 q与肌肉激活度 (关节力矩Qjoint) 均未知, 可视为优化变量. 因此, 预测动力学优化问题的自由度数一般很大.预测动力学优化将动力学方程式(8)视为约束条件, 此外一般还需给定运动的初值与终值, 以及其他一些事先规划的信息γ, 包括q, Qjoint的取值范围等. 上述约束条件限制了求解的可行域, 进而需要基于优化方法确定令目标函数J最优的步态.

预测动力学方法受制于优化求解器的计算能力, 研究工作主要局限于人体平面模型的多刚体系统动力学仿真, 难以引入神经与肌肉控制. Leboeuf 等(2006)讨论了最小力矩与最小能量假设对体操最优动作预测结果的影响. Xiang 等(2009)建立了人体的多刚体系统模型, 实现了单兵负重状态下的最优步态仿真. 随后, 其研究团队又建立了双人抬起重物模型(Xiang et al. 2019,Xiang & Arefeen 2020), 应用于人机功效领域. Jackson 等(2016)建立了跳远运动员的平面多刚体模型, 并根据实测运动学数据判断不同优化目标对跳远起跳动作的影响. Pettersson 等(2013)将原地起跳过程划分成多个时相, 分别以最小力矩为目标预测动作, 但这一方法的计算自由度数(约6000) 与约束数 (约15 000) 均比较高. Jansen 和McPhee (2020)基于直接配点法, 实现了自行车运动员冲刺动作的最优预测. 最近, Febrer-Nafría 等(2021)实现了不同步速条件下拄拐最优步态的三维预测.

为了实现人体动力学模型能够长时间维持站立、行走而不发生摔倒, 需要进一步引入非线性动力学分析工具, 理解人体多体系统的动平衡与稳定机制. 人体静止站立过程一般被视为以踝关节为转轴的单自由度倒立摆(Shumway-Cook & Woollacott 2007), 但Creath 等(2005)指出这一假设仅在外界扰动在1 Hz 以下时成立, 一般情况下应将人体视为髋-踝两级倒立摆系统. 基于这一假设, Chumacero-Polanco 和Yang (2020)分析了扰动对人体两级倒立摆系统平衡的影响, 讨论了Hopf 分岔与叉形分岔出现的条件. Günther 等(2016)进一步引入膝关节自由度, 提出三级倒立摆模型, 并指出调整下肢关节刚度能够实现从稳定吸引子到奇怪吸引子的转变. 针对人体两类平衡姿态的切换, 例如“坐站转移” (sit-to-stand) 问题, Shia 等(2018)提出使用倒立摆模型, 用吸引盆刻画人体跌倒的可能性(Holmes et al. 2020). 另外, 由于神经中枢到骨骼肌执行器存在几十到几百毫秒的时间延迟, 时间迟滞对人体姿态平衡的影响不可忽略(Stepan 2009). Zhang 等(2018)将踝关节肌群简化成含时滞的非线性控制器, 在人体摆模型中引入Hopf 分岔模式. 最近,Zelei 等(2021)与Molnar 等(2021)分别基于人体实验验证了含时滞比例-微分控制器形成的稳定域.

理解人体周期步态这一强非线性运动, 需要用到极限环分析行走周期过程的稳定性(Hürmüzlü 1986). 这一分析方法假设人体步态具有全局轨迹的稳定性, 但是不具有局部稳定性(何家玮 2018). 可采用庞加莱截面与最大Floquet 乘子, 定量判断人体运动学参数向理想极限环解的收敛情况(Hürmüzlü 1986). Dingwell 等(2001)进一步引入最大Lyapunov 指数, 分析双足步态受小扰动时的收敛率. 双足机器人的出现, 特别是McGeer (1990)提出的被动行走 (passive walking) 机器人, 为理解人体步态的非线性动力学提供了理想工具, 参见Al-Shukaet al.(2014)撰写的相关综述. Narioka 等(2009)在极限环行走双足机器人中引入气动人工肌肉, 分析了踝关节肌肉对双足行走稳定性的影响. 柳宁等(2008)采用胞映射法计算被动行走机器人的吸引盆,He 和Ren (2019)建立了含膝关节被动行走机器人的多体动力学模型, 实现了稳定步态参数的快速识别. 针对跑步(Bencsik & Zelei 2017)、跳跃等人体运动速度更快的情况, Zelei 等(2019)提出了包含关节主动力矩的平面模型, 寻找稳定运动过程满足的极限环. 另外, 同伦方法也能够应用在人体步态这一强非线性运动中. 例如, Howell 和Baillieul (1998)基于同伦方法分析了被动行走机器人的步态周期解; Gomes (2005)基于同伦方法, 寻找保能量的步态周期解; 最近, Ma 等(2021)将同伦方法与神经网络相结合, 提出了含假肢人体稳定行走控制策略. 然而, 非线性动力学分析往往局限于平面低自由度简化人体模型, 往往将骨骼肌行为过分简化, 忽略了真实的神经控制策略以及肌肉控制的冗余性特征.

4.2 个性化肌骨模型的参数辨识

肌骨多柔体系统动力学建模需要确定大量的模型参数, 但目前尚无实验手段能够从单一受试者辨识全部个性化参数. 因此, 目前一般采取“两步走”策略: 首先基于尸体解剖学数据建立所谓“标准人”模型, 然后通过标定手段映射到受试者. 但即便是标准人模型, 其生物力学参数也来源于多个受试组的结果. 因此, 如何整合基于不同受试者的模型数据, 已成为本领域研究的重要内容之一. 而肌骨系统个性化建模, 离不开多体动力学与影像学、运动生物力学、生物材料力学等人体实验测量学科的深度交叉.

4.2.1 肌肉形态

肌肉形态学参数, 特别是肌肉与骨骼附着点的选取直接决定了肌肉力臂. 一方面, 由于肌肉附着在骨骼上会形成附着曲面, 故基于影像直接选取肌肉附着点具有很大的随意性(She et al.2018). 另一方面, 解剖学界已建立了比较可靠的肌肉形态学数据库, 包括Horsman 等(2007)建立的下肢数据库, Erdemir 等(2015)建立的膝关节数据库, Hansen 等(2006)建立的腰椎数据库等.如何在测量受试者CT、核磁等影像学数据的基础上, 将肌肉附着点映射到个性化骨骼几何模型,是目前实现骨骼肌几何个性化的主要方案 (崔伟玲 2019), 参见梅齐昌等(2020)撰写的相关综述.

Kaptein 和van der Helm(2004)提出采用骨骼几何变换方法, 即通过对标准几何进行平移、旋转与放缩变换, 将标准人肌肉附着点映射到个性化模型. 但该方法只具有50%正确性. Li 等(2009)提出基于与骨骼固接的标记点配准韧带附着点, 但其方法基于尸体标本实现, 无法推广到健康受试者的无创测量. Pellikaan 等(2014)将点云配准中的迭代最近点法 (iterative closest point, ICP) (Arun et al. 1987)推广到肌肉附着点选取, 通过标准人与个性化骨骼几何点云实现最小二乘配准. 值得指出, ICP 方法是近年来生物力学领域关注的统计形状模型 (参见2.2 节) 的重要理论基础(Tsai et al. 2015, Luthi et al. 2018, 梅齐昌等 2020). Zhang 等(2016)基于26 例下肢几何影像数据建立了SSM 模型, 并将标准解剖模型的肌肉附着点数据映射到个性化受试者. 然而,SSM 模型需要大量解剖学影像数据作为训练集, 无法在小样本条件下使用.

Amberg 等(2007)在ICP 方法的基础上引入网格曲面的小变形, 建立了非刚性ICP 变换方法. 近期, 本文作者团队将该方法推广到肌肉附着点映射, 分别以de Zee 等(2007)建立的口颌模型的肌肉附着点, 以及一名典型健康受试者的肌肉附着区域为基础, 将模型映射到口颌肿瘤患者的术前CT 影像, 初步实现了口颌肌群与骨骼解剖的个性化自动配准, 参见图9. 该方法还能与Modenese 和Kohout (2020)提出的肌肉路径自动生成方法相结合, 实现受试者三维骨骼肌的个性化建模.

图9基于非刚性迭代最近点方法(Amberg et al. 2007)映射肌肉附着点. (a) 基于Anybody 标准口颌模型(de Zee et al. 2007)映射到患者, (b) 基于一名健康人肌肉附着区域, 映射到患者

除了肌肉附着点外, 以羽状角度量的肌纤维分布, 同样可能影响肌骨系统的动力学响应(李永胜 和 陈维毅 2007). Hodge 等(2003)应用超声影像观测了骨骼肌收缩时的三维形态变化. Manal 等(2008)进一步建立了肌肉激活度与羽状角变化之间的线性相关性, 但其肌肉收缩模式局限于等长收缩, 无法反映羽状角随人体运动的变化. 最近, Seynnes 和Cronin (2020)基于开源生物图像处理软件ImageJ, 开发了快速提取肌束与腱鞘几何的插件, 为提取羽状角的动态变化提供了计算工具.

4.2.2 肌肉最大力量

在肌骨模型中, 肌肉最大力量一般用最大收缩内力F0mus来表示, 其取值直接影响肌骨系统动力学响应. Valente 等(2014)的灵敏度分析结果表明: 骨骼肌几何和最大肌力会对逆动力学计算结果产生显著影响. 因此, 肌肉的最大力量已成为人体肌骨模型参数辨识的核心问题. 然而, 迄今尚无实验手段来直接测量单一肌肉的最大等长力量信息. 目前, 大多数肌骨模型的F0mus来自对尸体实验测定的肌肉生理截面积乘以固定的强度系数. 但该系数尚无定量实验支撑, 一般取0.2 ～1.4 MPa (Bruno et al. 2015). 此外, 还需要定义相关标度律 (scaling law) 将尸体实验测定的肌肉信息映射到个性化受试者. 例如: 可采用Rasmussen 等(2005)基于统计结果(Frankenfield et al. 2001)建立的线性标度律, Correa 和Pandy (2011)基于圆柱体肌肉几何假设推导得到的标度律, 以及Handsfield 等(2014)基于35 例MRI 测量结果建立的统计标度律. 然而, 这些标度律无法兼顾BMI、年龄、性别(Danneskiold-Samsøe et al. 2009)、劳动强度、是否患病等诸多因素, 难以直接应用在运动员、患者、士兵等特殊人群中.

等速肌力测试(Huang et al. 2017)是测量受试者肌肉力量的金标准, 但其无法分辨控制关节运动的肌力分配情况, 也无法测定肌肉力臂. 万祥林等(2020)通过动作捕捉测定腘绳肌力臂(Yu et al. 2008), 根据Ward 等(2009)给出的腘绳肌群各肌肉截面比例, 由等速测力计测得肌力强度和最优肌纤维长度. 然而, 该方法忽略了肌肉起止点与截面信息的个体间差异. Benoussaad 等(2013)基于Huxley 骨骼肌模型与等速加载测试, 辨识股四头肌主、被动肌力参数, 但实验过程需要电刺激控制, 难以应用到健康人群. Hayashibe 等(2011)提出基于力台与EMG 同时辨识肌肉质量分布与力量的计算方法, 但这一方法难以考虑深层肌群的贡献. Synek 等(2019)基于尸体实验, 反演人与灵长类动物的个性化手指肌肉参数, 但基于单一肌腱的加载方式难以实现在体无创加载. Hegarty 等(2019)使用手持式测力计测试小儿偏瘫患者的下肢关节肌群等长内力, 进而基于肌骨模型计算迭代获取肌肉力量, 但其使用的肌骨模型在肌肉几何上未实现个性化. Ma Y 等(2019)结合EMG 测量与肌骨模型仿真, 在无肌力测试的条件下实现小腿肌群的强度标定.最近, 李洋等(2021)提出了基于机器学习与有限元仿真的骨骼肌超弹性本构参数反演方法, 但该方法难以获得肌肉主动肌力参数. 另外, 大多数肌骨模型直接采用肌肉激活参数(例如: Thelen 2003), 忽略了不同人群与肌肉间的差异性. Sreenivasa 等(2016)将稳态、瞬态变量分别采用优化方法辨识, 给出了肱二头肌与肱三头肌的激活模式差异.

4.2.3 足底接触力描述

足与地面间的接触力决定了人体步态动力学响应. 步态实验室一般采用力台测量足底接触力, 测量结果包括三维力矢量与压力中心 (center of pressure, CoP) . 在肌骨模型中, 可直接将力台数据作为外载荷输入, 求解关节力矩与肌肉内力. 然而, 力台难以在步态实验室之外直接应用.此外, 在肌骨系统正向动力学分析中, 无法直接输入足底接触力. 足底压力测量可获取任意时刻足所受正压力的空间分布, 但其只包含支撑人体直立的法向压力, 难以获取推动人体前进的摩擦力. 因此, 肌骨系统建模需包含可靠的足底接触力模型.

在肌骨系统建模中, 一般将足底接触力处理为约束或接触模型, 其中约束建模适用于逆向动力学分析. Ren 等(2008)提出“光顺平移假设”, 采用经验函数拟合足底反力. Hamner 等(2013)建立了滚动约束模型模拟足与地面相互作用, 并通过与球铰和固定副(Guess 2012)约束比较验证模型适用性. Fluit 等(2014)在单足上布置12 个接触检测点, 在各检测点放置5 个虚拟作动器, 基于静态优化求解足与地面接触力分布. Skals 等(2017a)对这一约束模型做进一步优化, 应用于体育动作分析领域. 彭迎虎等(2019)基于力台测试对上述模型在不同步速条件下的正确性进行验证, 证实约束模型在低步速条件下具有较好的预测效果. Millard 和Mombaur (2019)将足分别简化成椭球与双球约束模型, 将约束建模方法推广到人体正向动力学仿真. 最近, Van Hulle 等(2020)提出基于最小二乘与滤波, 实现了足与地面单面约束力的快速计算.

接触力模型主要应用于正向动力学仿真. 由于足的复杂几何结构, 为了提高计算效率, 一般需将足简化成简单接触几何体的组合. 在被动行走(何家玮 2018)等问题的研究中, 可忽略足的三维几何, 在足底布置接触点, 将其与地面接触简化成分布点与平面接触问题(Ma et al. 2021).Jackson 等(2016)在足表面均布接触点, 在足与地面间形成线性刚度-阻尼器矩阵, 并基于参数优化获得接触参数. 然而, 可靠的接触点模型需建立大量接触对, 会给肌骨系统引入大量计算代价,可用简单几何体来拟合足部几何. 例如, Pàmies-Vilà等(2014)将足的接触几何简化成4 个球体,采用自适应协方差矩阵优化与增广Kalman 滤波优化接触模型参数. Shourijeh 和McPhee(2015)提出了超体积接触模型, 考虑足与地面接触过程中的非局部性. Lopes 等(2016)进一步将接触几何体抽象成椭球, 与点接触模型相比, 可提高接触计算效率. 如图10 所示, Brown 和McPhee (2018)基于步态周期的足底压力分布与压力中心轨迹实验, 对椭球接触模型的正确性进行验证. 类似的思想被Ezati 等(2020)进一步应用在人体步态轨迹优化当中. 接触模型与约束模型比较, 会带来更大的计算代价, 但其反映足与地面相互作用的力学本质, 适用于较高步速或惯性效应较大条件仿真.

4.3 典型应用

4.3.1 步态分析与假体设计

人体步态 (Gait) 是指人体步行时的人体姿态与肌肉激活特征. 正常稳定步态具有节律性, 一个完整的步态周期可定义为从一侧足跟触地到同侧足跟再次触地的过程, 并可进一步划分成支撑期与摆动期(Whittle 2014). 步态运动学信息主要包括髋、膝、踝关节屈/伸、内收/外展、内/外旋, 骨盆三维运动, 以及人体质心运动轨迹等(董玮 2011). 骨性关节疾病会影响步态特征, 除了改变步态周期等时相信息外, 还会造成步态运动学信息的定量改变(Ren S et al. 2018, Shi et al.2019). 然而, 目前尚缺乏在体实验手段, 测定步态运动学信息改变与骨骼肌激活方式的定量关联.

关节置换术是治疗大多数人体骨性关节疾病的有效手段. 但手术过程会不可避免地改变患者关节接触曲面形貌, 切断部分肌肉与韧带组织, 调整其他肌肉力臂, 容易引起患者术后步态异常(Benedetti et al. 2003), 影响患者术后日常生活. 根据北京积水潭医院的一项统计结果(Tang et al. 2014), 16.3%的患者对术后康复效果不满意, 主要体现在步态异常、下蹲困难、肌力下降等. Bergmann 等(2001)测量了3 名患者的人工髋置换术后步态, 基于人体多刚体节段模型逆向求解关节三维载荷, 建立了开源数据库Hip98. 该数据库已成为人工髋关节设计的重要依据(Bergmann et al. 2016), 但其并未考虑髋臼与球头接触, 同时忽略了髋关节周围软组织与肌肉的力学影响. 此外, 基于红外贴点的传统步态分析需要受试者长时间实验准备, 难以拓展到患者大样本临床评测实践.

肌骨系统多柔体动力学建模与计算方法为理解关节置换对步态动力学的影响机制提供了定量分析手段. Modenese 等(2011, 2012)基于Hip98 数据库, 分析了髋关节置换患者术后人工关节载荷分布及骨骼肌激活方式, 并与实验测量结果定量比较, 但其研究忽略了髋关节置换导致的肌肉功能与关节旋转中心变化. Navacchia 等(2016)实现了肌骨多体模型与人工膝关节精细有限元模型的联合仿真, 逆向求解肌肉内力与关节接触压力中心. Stylianou 等(2013)基于弹性理论(Blankevoort et al. 1991)建模人工膝关节接触, 正向求解下蹲过程中的肌骨系统载荷, 但其难以拓展到步态大范围运动的正向求解. Chen 等(2016)提出正-逆向耦合求解人工髋(Zhang et al.2015)、膝关节(Chen et al. 2016)载荷, 但下肢关节运动仍需基于贴点步态分析结果输入.

图10足底接触力模型(Brown & McPhee 2018). (a)椭球接触模型, (b)实验与仿真足底压力结果比较

本文作者团队建立了包含8 台红外相机阵列与4 台视频相机的人体动作同步采集实验系统,参见图11(a). 该系统能同时发挥红外动捕高精度与视频AI 快速分析的优势, 在减少红外贴点数目、显著缩短测量周期的同时, 解决了AI 人体关键点分析无法准确求解内/外旋角度的问题, 参见图11(b). 最近, 作者研究团队将上述分析方法与CT 影像配准相结合, 实现了骨盆与股骨运动姿态的精准测量, 避免了传统贴点方式带来的不确定性与系统误差, 进而能直接应用在人工关节安装角度术前规划中. 高精度步态测量也为肌骨系统逆向动力学仿真提供了可靠的运动学数据输入, 该方法可结合4.2.1 节肌肉形态个性化方法, 给出髋关节肌群在人体运动过程中的长度与力臂变化.

4.3.2 脊柱降载

脊柱是人体的中轴骨骼, 具有支撑与保护胸、腹腔脏器, 负担头-足向载荷, 降低传递到头部振动等作用. 理解脊柱肌骨系统承载机制, 对提高举重运动成绩(Wei et al. 2012)、避免重物搬运引起运动损伤(Arjmand & Shirazi-Adl 2005)、加快脊柱侧弯康复(Shayestehpour et al. 2021)具有重要意义. 然而, 目前对脊柱动力学功能进行评测只能通过表面肌电 (Wei et al. 2012)、等速加载(Bae et al. 2010)等手段, 难以定量分析腰大肌、多裂肌、腹横肌等深层肌群的工作机制, 以及脊柱在复杂运动条件下肌力如何分配.

肌骨系统动力学建模, 可为理解人体脊柱的承载机制提供定量仿真分析手段. 近年来, 脊柱肌骨建模领域的研究重点之一在于如何建立这一复杂刚柔耦合多体系统的动力学模型, 参见Dreischarf 等(2016)的相关综述. Arjmand 与Shirazi-Adl 团队针对脊柱静力学仿真进行了系统研究, 建立了胸腰椎肌骨模型(Arjmand & Shirazi-Adl 2005), 使用静态优化假设计算对称(Arjmand et al. 2011)与非对称载荷(Arjmand et al. 2010)条件下的骨骼肌内力, 并探讨腹内压(Arjmand & Shirazi-Adl 2006a)、肌肉缠绕路径(Arjmand et al. 2006)、脊柱侧弯(Kamal et al.2019)对腰椎载荷分布的影响. Christophy 等(2012)基于OpenSim 建立了腰椎肌骨逆动力学模型, 假设各椎体与骨盆运动满足固定的角度分配节律, 但实验表明腰椎运动节律随躯干屈曲角度不断变化(Tafazzol et al. 2014). Bruno 等(2015)将Christophy 模型推广到胸腰椎, 并引入可变形胸腔. Ignasiak 等(2016a, 2016b)进一步证实, 胸腔建模假设主要影响上半部分腰椎载荷.Putzer 等(2016)系统探讨了椎体解剖学参数对逆动力学仿真结果的影响, Bruno 等(2017)进一步证实受试者脊柱曲线与肌肉形态决定了肌骨仿真结果的精度. Khurelbaatar 等(2015)建立了包含全离散颈、胸、腰椎节段的脊柱肌骨模型. 另外, Rupp 等(2015)建立了腰椎正向动力学模型,成功仿真脊柱主动前屈动作. Mörl 等(2020)进一步实现机械驱动脊柱被动屈曲条件的正向仿真.

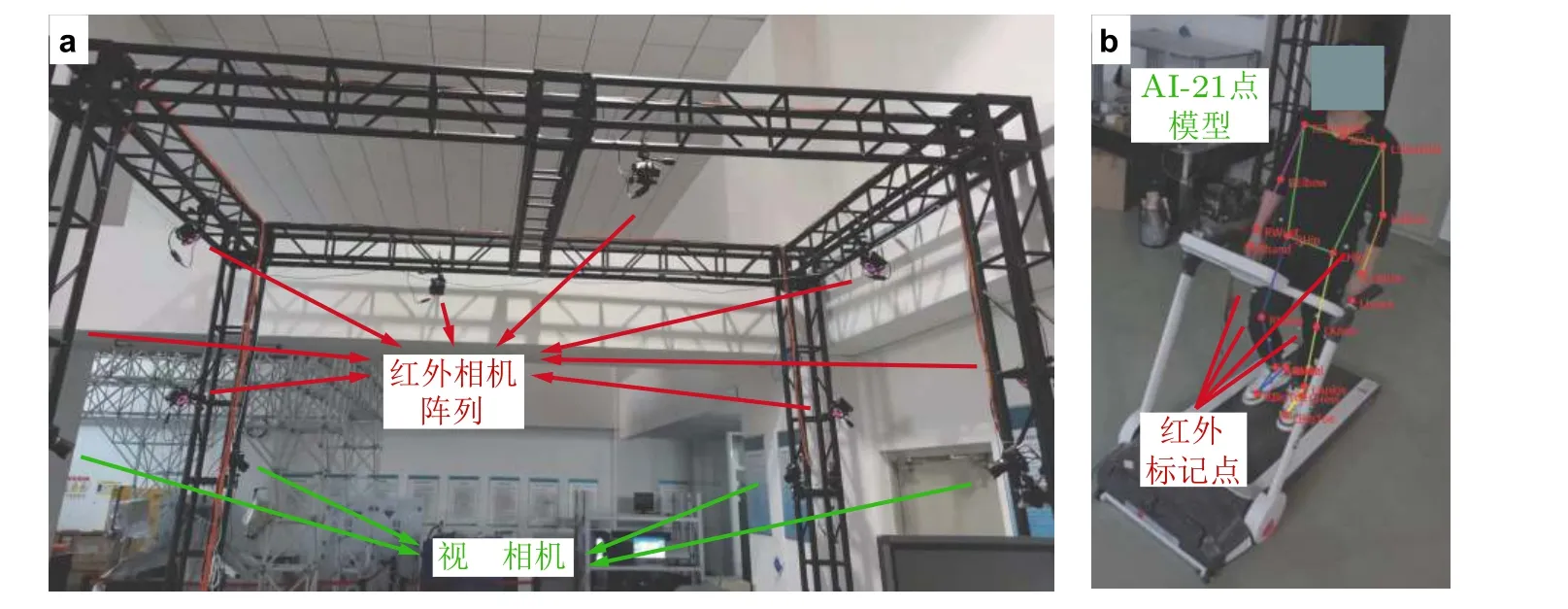
图11人体步态同步测量方法. (a)红外与视频混合动作捕捉系统, (b)视频AI-21 点模型与红外标记点同步测量

与四肢肌骨系统相比, 脊柱除了骨骼、肌肉、韧带等承力结构外, 还包括椎间盘这一重要的被动承载结构. 椎间盘连接相邻椎骨, 由其中央承受正压力的髓核, 以及包裹在髓核周围, 具有弯曲与剪切刚度的纤维环组成. 为了方便起见, 在逆动力学模型中常将椎间盘简化成球铰(de Zee et al. 2007, Bruno et al. 2015), 忽略了椎间盘的变形与刚度特性. 为了描述椎间盘同时承受由躯干与头颈部与传递的6 自由度载荷, 一种方式是将其抽象成线性Bushing 模型, 建立6 × 6 对称刚度矩阵. Gardner-Morse 和Stokes (2004)基于尸体实验将椎间盘简化为并联的压杆-剪切梁, 对应的刚度矩阵具有11 个独立变量. Christophy 等(2013)证实, 椎间盘Bushing 起止点对计算结果影响显著. Meng 等(2015)将Bushing 模型应用在Bruno 腰椎模型中, 模拟相邻椎体间的相对滑移, 但其线性刚度与阻尼矩阵忽略了椎间盘所具有的非线性特征. Monteiro 等(2011)建立通过椎间盘有限元模型确定线性刚度矩阵系数的方法. Karajan 等(2013)进一步将离散刚度模型推广到非线性情况, 但该模型无法将椎间盘模型与肌骨模型强耦合仿真. Arjmand 和Shirazi-Adl (2006b)采用柔性剪切梁模型连接相邻椎体, Valentini 和Pennestrì (2011)进一步采用弹性样条拟合脊柱曲线, 分析头足向振动传递(Valentini 2012).

除椎间盘外, 腹腔本身也能够承担一部分头足向压力. 腹腔内除了液体脏器外, 在食管、胃泡与其他脏器间隙中均存在一定体积的气体(Levitt 1971, Fink & Lembo 2001, Hui et al. 2005), 该气体的压力称之为腹内压 (intra-abdominal pressure, IAP) . 如图12(a)所示, 外载荷增大会减小腹腔体积, 导致腹内压增大, 进而产生向上的合力支撑胸腔(Daggfeldt & Thorstensson 1997,Cholewicki et al. 1999), 降低椎间盘压力. 然而, 部分学者(Cholewicki et al. 2002, Arjmand &Shirazi-Adl 2006a)指出, 腹内压升高可能会伴随腹壁肌群激活度提高, 抵消腹内压的降载效果.现有肌骨模型大多忽略腹内压效应, 即便考虑腹内压也将其简化为随脊柱前屈角度变化的合力(Arjmand & Shirazi-Adl 2006a, Meng et al. 2015), 或能够抵抗压应力、激活度由外载荷决定的类肌肉元件(Arshad et al. 2016, Liu et al. 2019), 无法考虑腹内压升高与腹壁肌群激活度的耦合.

为解决这一问题, 本文作者团队提出了腹内压气柱模型(Guo J et al. 2021a), 将腹内压与腹横肌、膈肌等核心肌群激活度联系起来. 如图12(b)所示, 首先采用肌肉膜单元离散腹壁肌群与膈肌, 并认为上述膜肌肉与骨盆 (盆底肌) 围成的体积与腹腔内气体体积线性相关. 在此基础上,将图12(c)所示的腔内气体简化为等温理想气体, 根据理想气体状态方程计算腹内压, 同时考虑脏器重力引起的腹内压垂向分布. 进一步, 将腹内压垂直作用于肌肉膜单元离散的膈肌, 提供竖直向上的合压力支撑脊柱与胸腔. 本文作者团队将腹内压气柱模型与全脊柱肌骨模型耦合, 证实脊柱前屈时核心肌群激活能够提升腹内压, 进而降低椎间盘轴向压力与竖脊肌内力. 该建模方法被进一步应用在飞行员对抗头足向过载中, 证实飞行员抗荷所做的呼吸抗荷动作(耿喜臣等2002)除了能够保证头部供血外, 还能够降低后伸、直立等动作条件下的腰椎间盘载荷, 从而降低飞行员出现腰背痛的风险.

4.3.3 口颌植入物设计

据统计, 口腔颌面部恶性肿瘤约占全身恶性肿瘤的3% ～ 5%, 全球每年新发病例超过60 万(郑家伟等 2010). 目前, 对口腔恶性肿瘤的早期患者以手术治疗为主, 但肿瘤及手术所造成的颌骨缺损, 可能导致患者术后出现张口受限(Pauli et al. 2016). 根据Watters 等(2019)基于636 篇文献的分析结果, 患者出现张口受限的比率从术前的17.3%升至术后6 个月的44.1%. 此外, 颌骨切除会造成下颌偏斜、颞下颌关节紊乱等口颌系统功能异常, 严重影响患者的生活质量和社会功能. 因此, 如何提升患者术后口颌运动功能, 具有重要的临床医学意义. 然而, 现有实验测量只能监测患者下颌运动及浅表咀嚼肌的肌肉放电功能(王晶等 2019), 无法揭示口颌运动过程中肌群内力分配机制与预测颞下颌关节载荷.

对口颌肌骨系统进行多体动力学建模, 可为实现上述目标提供数值仿真手段, 参见Hannam(2011)撰写的相关综述. 1997 年, Koolstra 等(1997)建立了包括颅骨和下颌骨的下颌动力学模型.Hannam 等(2008)在模型中引入了刚性舌骨, 并针对下颌骨重建患者开展仿真. Koolstra 和van Eijden (2004)在口颌肌骨模型中引入颅骨协同运动. Tuijt 等(2010)使用样条曲线拟合颞下颌关节接触面, 分析开口与闭口运动中颞下颌关节载荷的差异, 并通过正向仿真解释了肌肉松解治疗关节脱位的动力学机制(Dicker et al. 2012). 最近, Sagl 等(2019)对关节盘进行有限元建模, 给出了口颌运动过程中的关节盘应力分布. 然而, 上述肌骨模型均为标准人模型, 忽略了患者间的口颌肌骨系统功能差异. 另外, 肌骨模型参数与神经与肌肉控制均根据健康受试者确定, 没有考虑肿瘤及手术导致的开口肌切除与失神经支配(Ishida et al. 2015)、肌肉截面积减小(Curtis et al.1999)、肌肉组织纤维化等变化.

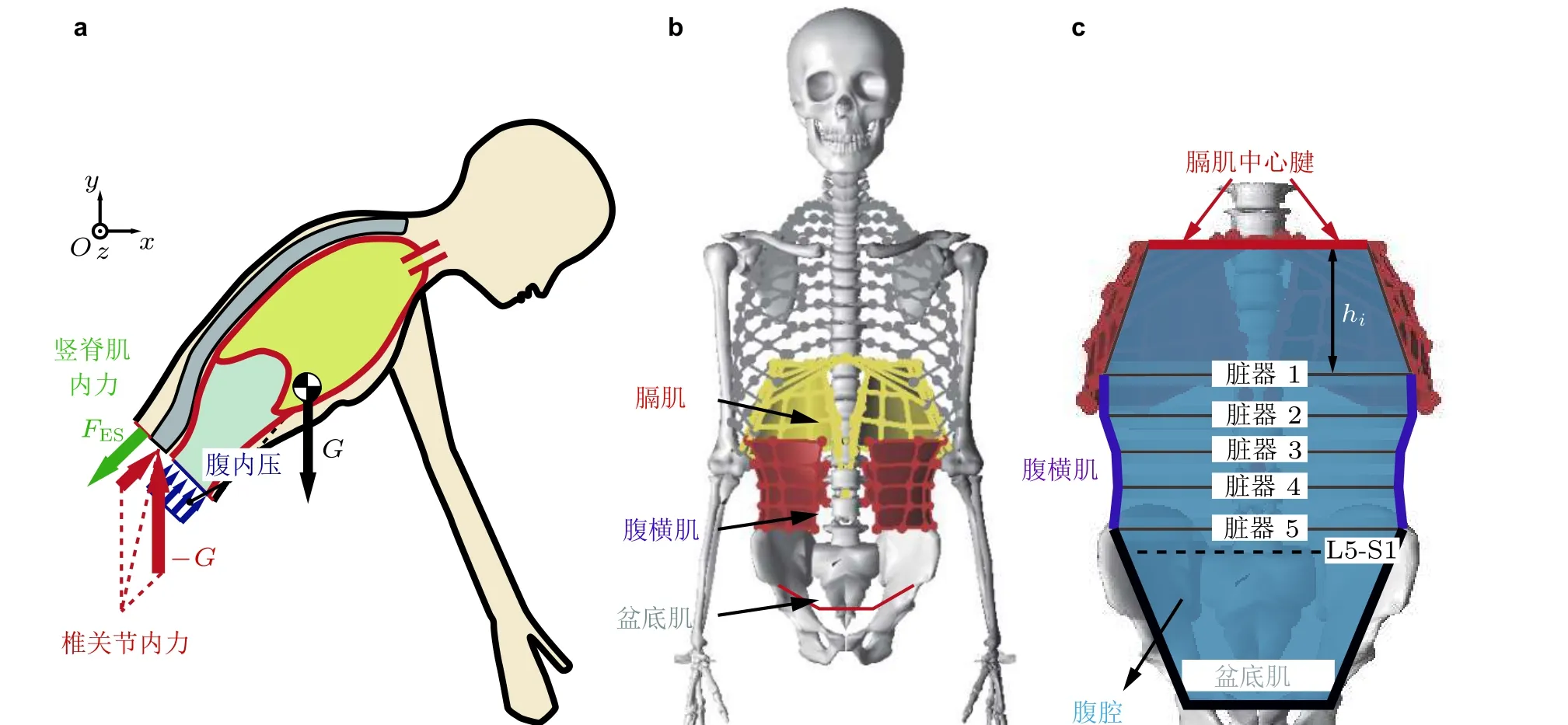
图12腹腔多柔体动力学模型(Guo J et al. 2021a). (a)躯干隔离体受力分析, (b)柔性核心肌群模型,(c)腹内压气柱模型

本文作者团队与北京大学口腔医院颌面外科王晶博士、陈俊鹏博士等合作, 提出了健康人与患者口颌肌骨系统个性化多柔体动力学建模方法. 根据CBCT 拍摄受试者颌面骨骼几何数据,通过患者个性化几何数据样条拟合得到颞下颌关节窝与髁突接触面. 如图13(a)所示, 基于Zebris 电子面弓采集受试者大张口过程的下颌骨刚体运动, 并基于贴附在上颌的颌板标记点配准静态CT 与运动轨迹数据. 进一步, 基于逆向动力学仿真确定大张口运动过程中的肌束长度变化, 作为二腹肌等降颌肌群牵张反射的控制目标. 咬肌、颞肌激活度根据实测EMG 翻正滤波后由式(4)确定. 在此基础上, 通过正向动力学仿真求解降颌肌群激活度与颞下颌关节接触行为, 并根据最大张口时的二腹肌激活度缩放降颌肌群最大主动肌力F0mus. 正向仿真能够基本复现下颌骨与髁突运动轨迹, 仿真得到的下切牙点运动轨迹与4 名受试者实测结果均方根误差为3.7 ± 1.3 mm.

在此基础上, 该合作团队结合肌骨动力学仿真与临床生物力学测量, 提出了基于术后早期张口度预测的口颌植入物初步设计方案. 首先, 基于北京大学口腔医院建立的颌骨肿瘤患者生物力学信息数据库(王晶等 2019), 统计患者术后早期的肌肉长度变化、截面积缩减、咀嚼肌峰值EMG 变化等平均结果, 调整个性化肌骨模型参数与升颌肌群激活度. 在此基础上, 以术前正向动力学仿真得到的肌肉激活度曲线作为图13(b)所示术后早期模型输入, 并改变截骨尺寸、植入物下颌角等变量, 找到令仿真得到的张口度最大的植入物设计值.

5 结论与展望

本文主要针对人体肌骨多柔体系统动力学研究, 较为系统地回顾与总结骨骼肌解剖结构与生物力学建模、神经与肌肉控制原理与数学描述、肌骨系统动力学问题分类与求解方法、以及肌骨模型在多学科领域潜在应用等研究进展. 一方面, 人体肌骨系统的多体动力学研究已取得长足进步; 在骨骼肌主、被动本构关系, 肌肉与骨骼相互作用, 神经-肌肉控制的冗余问题求解, 个性化建模等重要领域形成了较为完善的研究范式与体系. 另一方面, 已建立的肌骨多柔体动力学模型能够获得运动生物力学实验难以测定的关节力矩、肌肉内力等信息, 为提高运动能力、避免运动损伤、加快康复进程提供了数值分析手段, 在临床医学、竞技体育、军事训练、人机工程等领域具有广泛的应用前景.

然而, 已有研究对人体肌骨多柔体动力学与控制的研究仍有很多不足, 例如: 大多聚焦基于Hill-Zajac 模型的肌骨系统建模及优化控制算法, 缺乏对骨骼肌微纳米结构与三维几何、肌筋膜跨肌肉传力、韧带/肌腱黏弹性、神经与肌肉多层级分布控制、肌骨系统与呼吸/血流的耦合(李娟等 2013)等问题的深入研究, 如下方向需要开展进一步深入探索:

(1) 复杂真实的骨骼肌建模方法. 基于多柔体系统动力学建模理论, 充分借鉴医学影像学、解剖学、生物材料力学领域的研究成果, 突破Hill-Zajac 建模框架的局限性, 赋予骨骼肌以真实的体积、质量、截面积与激活度分布.

(2) 建立自主智能的肌骨模型. 综合神经与肌肉控制存在的协同性、多级性、肌肉功能差异、模糊控制等特征, 提出正-逆向耦合肌骨动力学算法, 简化对肌肉的非线性特征描述, 加快计算效率.

(3) 形成体医工交叉融合平台. 以肌骨动力学模型为计算内核, 面向临床医学、体育工程、虚拟现实等需求, 构建手术植入物设计工具、运动员智能打分工具、增强现实物理引擎等, 由数值仿真模型升级为数字孪生人与虚拟设计的共性基础与关键技术.

(4) 设计新一代人机共融装备. 融合肌骨动力学与机器人学, 面向主动健康、精准康复等需求, 设计新一代康复辅具(蒲放和樊瑜波 2013)、损伤防护(王丽珍和樊瑜波 2020, 栗志杰等2020)、仿生软体机器(尹顺禹等 2020)等共融机器人产品与定制化方案.

(5) 推动神经科学与类脑智能发展. 一方面, 肌骨动力学仿真能够验证并指导神经运动增能(傅维杰 和 刘宇, 2020)产品设计, 服务科技奥运与主动健康需求. 另一方面, 肌骨动力学模型可作为强化学习网络的物理引擎, 训练新一代高性能自适应神经网络, 不断趋近甚至超越人体神经运动控制机制(Kidziński et al. 2018).

致 谢 国家自然科学基金青年基金(12102035), 中国博士后基金站前特别资助(2020TQ0042), 国家杰出青年科学基金(12125201). 感谢北京航空航天大学王丽珍教授、北京体育大学刘卉教授以及匿名评阅专家对本文提出的修改建议.