一种永磁同步电机凸极信号测量方法

麦志勤， 肖飞， 刘计龙， 付康壮， 牧雅璐， 李科峰

(海军工程大学 舰船综合电力技术国防科技重点实验室，湖北 武汉 430033)

0 引 言

当前，高频电压注入法是实现永磁同步电机(permanent magnet synchronous motor，PMSM)零低速区转子位置估计的主流方法[1-3]。通常情况下，该方法额外地将高频正弦电压注入至电动机定子绕组，提高了零低速工况信噪比，进而有助于从高频响应电流中估计转子位置信息。按照高频电压注入的形式，可分为高频旋转电压注入法和高频脉振电压注入法[4-5]。

基于高频电压注入的转子位置估计方法依赖于PMSM磁场凸极水平[6]。磁场凸极又可称为空间凸极或主凸极，其本质为由于永磁体在转子空间分布位置的特殊性，导致交、直轴磁路不对称的现象，具体表现为交、直轴电感不相等[8-9]。电动机磁场凸极水平越高，交、直轴电感差异越大，越有助于高频电压注入法实现转子位置估计。正常情况下，可认为电动机仅含有主凸极，但实际上受到注入高频电压畸变、磁场饱和以及空间磁链高次谐波等非理想因素影响，电动机容易产生次凸极。通常，主凸极与次凸极并存的现象称为电动机的多凸极效应[10-12]。

多凸极效应的危害在于降低主凸极信号的信噪比，甚至淹没主凸极信息，对位置观测器带宽、位置估计精度以及电动机运行效率产生负面影响，严重时甚至引起转子位置估计失败[13-14]。因此，若想利用高频电压注入法实现永磁同步电机零低速区转子位置估计，必须对被选电动机的凸极性进行提前评估。一方面需要考察被选电动机的主凸极水平，从而判断该电机是否适合采用基于高频电压注入的转子位置估计方法[15]。另一方面，需要考虑被选电动机的次凸极强度，若次凸极强度过大，则需进一步对次凸极进行抑制，否则次凸极将影响转子位置估计的正常进行[16]。

电动机的凸极性一方面可通过有限元仿真分析进行直接仿真计算，另一方面可通过实验测量方法进行测量。值得考虑的是，对于市场上购买的成品PMSM，其有限元模型通常难以获得。此外，文献[20]指出对于部分PMSM甚至可能出现次凸极强于主凸极的现象，如该文研究的集中绕组表贴式永磁同步电机(concentrated windings，cwSPMSM)，于是另辟途径采用基于二次谐波凸极的转子位置估计方法。可见，设计可行有效的凸极性实验测量方法，提前分析被测电机凸极性分布规律，对实现PMSM高频电压注入转子位置估计具有重要意义。

文献[21]利用高频脉振电压注入法进行转子位置估计，同时研究了永磁同步电机主凸极强度的测量方法，该文的试验电机为表贴式永磁同步电机。该方法为了测量样机的主凸极强度，首先在机械式位置传感器的帮助下，利用辅助固定机构将转子位置锁定在0°。然后，令估计同步坐标系以某一固定角速度顺时针旋转，从而实现真实同步坐标系与估计同步坐标系之间相位差的连续变化。最后绘制高频电流幅值随相位差连续变化的电流圆，以电流圆半径长度衡量被测电动机的主凸极强度。文献[18]所提方法需要采用固定机构将电动机转子锁定，该方法对于小功率等级的电动机实现较为简单，但对于大功率电动机则对固定机构的机械强度提出了很高要求，增加了实验测试的难度与成本。此外，该文没有对次凸极的测量方法展开研究。

文献[22]对开关磁通永磁同步电机的主凸极及次凸极测量方法进行了研究。在主凸极强度测量时，其方法与文献一致；在次凸极信息测量时，其利用机械式位置传感器将电动机控制于真实d-q坐标系，然后在电动机静止工况下直接向d轴注入高频脉振电压，并根据高频响应电流幅值的波动情况判断被测电机是否存在次凸极现象。该文探索性地面向高频脉振电压注入法对永磁同步电机的多凸极效应进行了研究，具有一定的开创意义。然而，由于被测电动机的多凸极效应较弱，对高频电压注入法转子位置估计的影响较小，仅定性地判断被测电动机是否存在多凸极效应，没有对次凸极的特征信号进一步定量测量与分析。

为此，为了提高测量方法的普适性，本文提出一种基于高频脉振电压注入法的PMSM凸极性实验测量方法。所提方法在电动机旋转过程中完成凸极性测量，无需采用任何固定结构，并且可同时测量被测电动机的主凸极水平、次凸极特征信息(如幅值和频率)以及不同负载工况下的交叉饱和角。通过测量上述特征信息，有助于实现PMSM高频电压注入转子位置估计，并可优化转子位置估计性能。最后，分别在一台内置式永磁同步电机(interior permanent magnet synchronous motor，IPMSM)与表贴式永磁同步电机(surface-mounted，SPMSM)上对所提方法的可行性进行验证。

1 高频脉振电压注入法

本文基于高频脉振电压注入法实现PMSM凸极性测量，本节对其原理进行简要介绍，并且分别建立仅考虑主凸极的高频电流模型以及同时考虑主凸极与次凸极的高频电流模型。

1.1 考虑主凸极的高频电流模型

图1 不同坐标系的相位关系

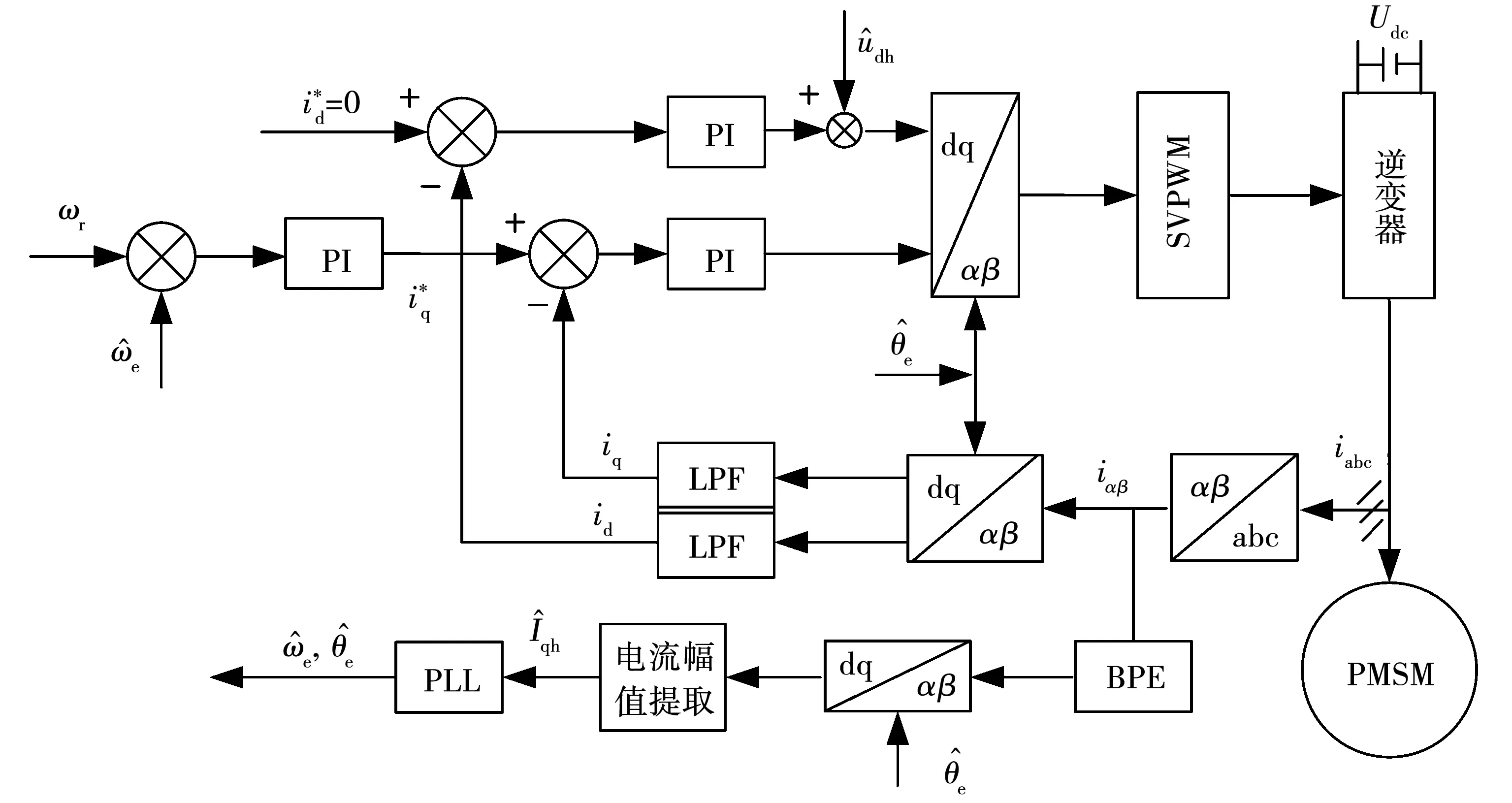
图2 高频脉振电压注入法位置估计原理框图

(1)

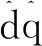
(2)

(3)

(4)

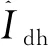
(5)

1.2 考虑主凸极与次凸极的高频电流模型

文献[18]指出，电动机的次凸极可分为静止凸极与谐波凸极两种。静止凸极不受转子位置影响，其既与电动机定子绕组非对称相关，也与不平衡的高频电压激励、电流传感器测量零偏以及模数转换误差等因素相关。相反，谐波凸极受转子位置影响，其频率与主凸极频率存在一定倍数关系，诱因通常包括定子绕组离散分布、定子绕组开槽、安装误差以及磁场饱和等。

式(2)描述了正常情况下的高频电流表达式，在此状态下高频脉振电压注入法的转子转速与位置估计结果均较为平滑。然而，若被选永磁同步电机存在多凸极效应，在高频脉振电压信号作用下电动机定子绕组将产生与次凸极相关的高频电流成分。借鉴文献[18]与文献[21]的建模方法，考虑多凸极效应时高频脉振电压激励下的高频响应电流可表示为

(6)

式(6)所示的高频电流幅值中：Idn0与Iqn0代表由静止凸极引起的电流成分，该成分不随转子位置改变而改变，表现为直流偏置；Ip、Incos(2Δθ+φ2)与Insin(2Δθ+φ2)代表由主凸极产生的电流成分，为了便于区分主凸极的幅值与相位均加入下标“2”。最右端求和部分代表谐波凸极引起的电流成分；h代表谐波凸极的阶次；Inh代表谐波凸极的幅值；φh代表谐波凸极的相位。谐波凸极为交流分量，其频率与主凸极频率存在一定倍数关系，变化规律受转子位置影响。

上述分析表明，当被测电动机发生多凸极效应时，交轴与直轴高频响应电流的幅值将出现非理想的直流偏置与谐波成分。然而，这些成分的幅值、频率以及相位信息均未知，并且这些非理想成分与电动机定子绕组非对称、不平衡的高频电压激励、安装误差以及磁场饱和等因素相关，不同电动机驱动系统难以建立统一的数学模型进行描述。为此本文提出一种永磁同步电机凸极信号测量方法，其原理于后文进行介绍。

2 传统的电动机凸极信号测量方法

2.1 凸极信号的测量原理

为了介绍永磁同步电机凸极信号的测量原理，将式(2)改写成如下形式，即

(7)

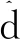
2.2 传统凸极信号测量方法及其实现

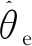
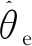
图3 传统凸极信号测量方法的坐标关系

由上述介绍可知，文献[21]与文献[22]所提方法需要采用固定机构将电动机转子锁定，凸极信号的测量是在电机静止状态实现的。对于小功率等级的电动机驱动平台，该方法的实现较为简单。但是，对于大功率电动机驱动平台，该方法对固定机构的机械强度提出了很高要求，一定程度增加了实验测试的难度与成本。此外，上述两篇文献均没有对次凸极的测量方法展开定性分析，无法为电动机多凸极效应的抑制提供有效信息。

3 改进的电动机凸极信号测量方法

为了克服上述问题，本文采取固定估计位置，改变真实位置的方法。图4为本文所提改进型凸极性信号测量方法的坐标关系。所提方法通过软件设计的方法将估计位置设置为0°，然后利用常规的矢量控制技术将真实转子位置θe逆时针旋转，同样成功构建了位置误差Δθ的连续变化量。

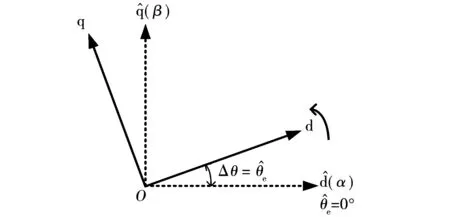
图4 改进型凸极信号测量方法的坐标关系

3.1 改进型凸极信号测量方法的实现

图5 永磁同步电动机凸极信号测量原理框图

以下对本文所提凸极信号测试方法的数学原理进行说明。首先在估计同步坐标系注入高频脉振电压，经过反Park坐标变换后，从两相静止坐标系的角度看，实际应用时注入的高频电压为

(8)

(9)

由式(9)可见，关闭高频脉振电压注入法位置估计环节时常规的高频脉振电压注入法改变为在静止坐标系实现的高频脉振电压注入法。

(10)

(11)

式中，NF代表陷波器(notch filter，NF)。本文采用陷波器滤而没有采用常规的低通滤波器除2倍频高频谐波，其原因分析如下。根据式(3)，Ip分量正比于d轴电感与q轴电感之和Lqh+Ldh，而In分量正比于d轴电感与q轴电感之差Lqh-Ldh。对于电感参数较小的SPMSM，In本身非常微小，而Ip却远大于In(可相差2～3个数量级)。此时，对滤波能力提出了很高要求，一旦滤波能力不足，凸极信息将被淹没，从而无法判断电动机凸极性以及实现转子位置估计。考虑到陷波器因具有特定频率谐波强陷波能力，利用其提取In的方法适用于不同参数的永磁同步电动机，普适性更强。

相较于传统电动机凸极信号测量方法，本文所提方法的优点在于电动机的凸极信号测量是在电动机旋转过程中完成，无需采用任何固定结构，可适用于不同功率等级的电机驱动平台，有效降低实验测试的难度与成本，提高了方法的工程适用性。此外，所提方法可同时测量被测电动机的主凸极水平、次凸极特征信息(如幅值和频率)以及不同负载工况下的交叉饱和角。

3.2 凸极信号的分析方法

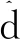
1)根据电流圆半径In的长度判断主凸极强度。在某一注入电压-频率比配置下，根据偏心圆半径长度可直观判断电动机的主凸极性强度，若半径较长且清晰可辨，说明该电动机的凸极性较强，被测电动机在该电压-频率比配置下可利用高频注入法实现转子位置估计；反之，若半径较短难以辨认，可通过增大电压-频率比来增大In，直至其达到一定幅值以满足位置估计的需求；极端情况下持续增大电压-频率比直至驱动变频器过流保护，In依然很小，说明被测电动机不适合利用高频注入法实现转子位置估计。

2)根据电流圆形状与位置判断是否存在多凸极效应。前文指出，静止凸极在高频脉振电压注入法中表现为在高频电流幅值叠加一定的直流成分，此时电流圆圆心将偏离Y轴0刻度水平线，如图6(b)所示。若被测电动机的电流圆形状与图6(b)相似，可判断被测电动机存在静止凸极，此时需要进一步对不同负载工况下的静止凸极强度测量。同理，谐波凸极在高频脉振电压注入法中表现为在高频电流幅值叠加一系列交流谐波成分。若被测电动机同时含有静止凸极与谐波凸极，被测电动机的电流圆圆心不仅偏离Y轴0刻度水平线，而且电流圆形状发生畸变，如图6(c)所示。若被测电动机的电流圆形状与图6(c)相似，说明被测电动机同时存在静止凸极与谐波凸极。此时，需要进一步分析。

图6 永磁同步电机凸极性示意图

多凸极效应使位置估计产生误差，且误差随转子位置改变而改变，从而对转子位置估计精度、位置观测器带宽、电动机运行效率产生负面影响，严重时甚至引起转子位置估计失败。此环节的测量意义在于根据测量的次凸极的幅值与频率信息，有目的地配合特定多凸极性消除方法，降低多凸极效应对位置估计性能的影响。

4 实验结果与分析

本节对本文所提的PMSM凸极信号测量方法进行实验验证。为了验证更加充分，分别在一台IPMSM与SPMSM上进行凸极性测量。实验电机如图7所示，#1号电机为IPMSM，#2号电机SPMSM，并且图7上方给出了两台电机的部分参数。#1号电机与#2号电机通过联轴器连接，当#1号电机作为被测对象时#2号电机作为发电机，定子绕组接三相平衡电阻负载用于消耗功率，反之亦然。为了便于调试，实验时仅改变注入电压幅值，注入频率保持为300 Hz，等效于改变注入高频电压的幅值-频率比，直流母线Udc=500 V。

图7 测试电机

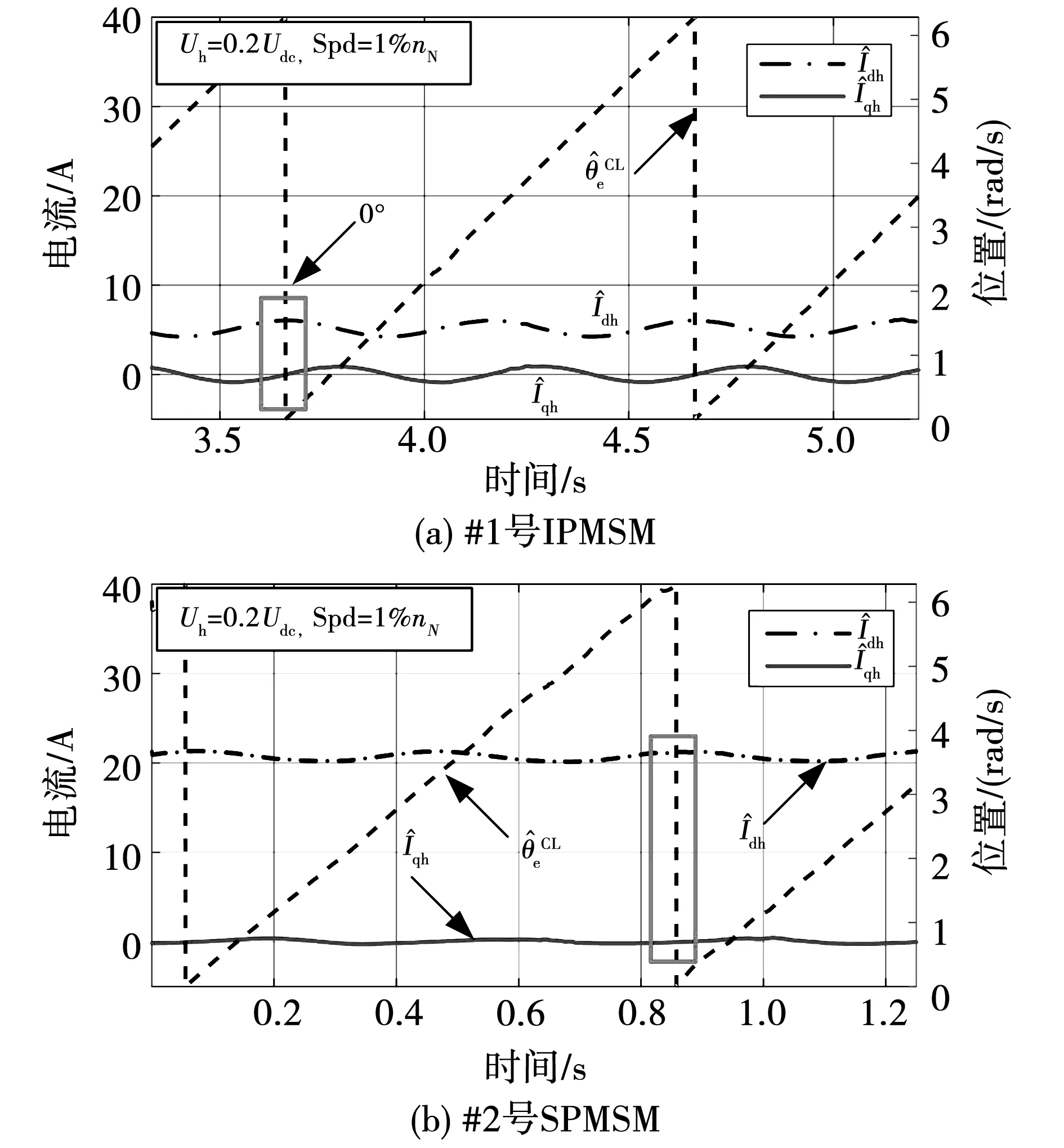
图8 空载工况下高频响应电流幅值与转子位置实验结果

4.1 #1号IPMSM凸极性测量及分析

在#1号IPMSM上对本文所提的凸极信号测量方法进行验证。为了避免交叉饱和效应的影响，电动机工作于空载工况。

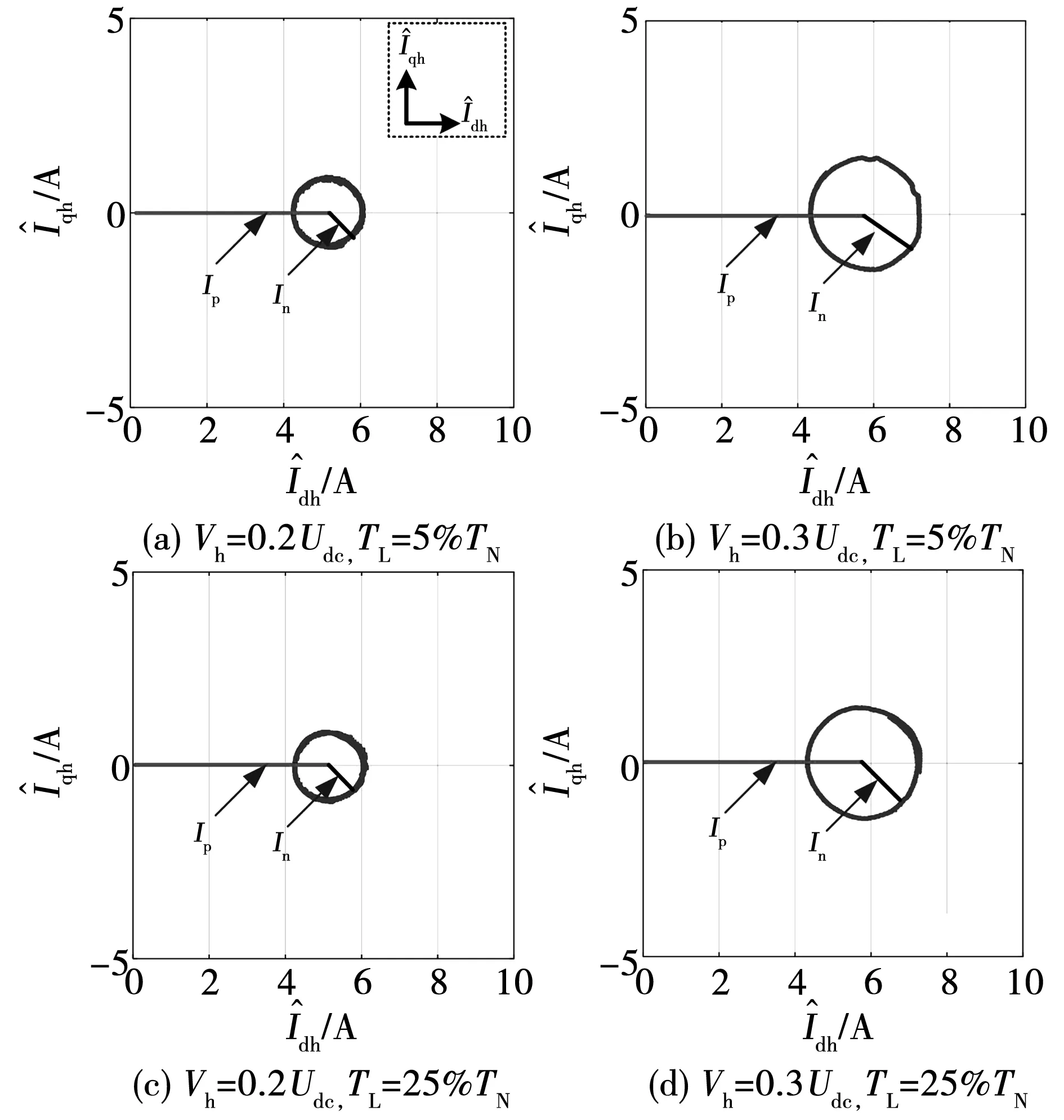
图9 不同转速工况下的电流圆实验结果(#1 IPMSM)

由实验结果可以看出，一方面，电流圆半径较长且清晰可见，说明电动机具有良好的凸极性，这与该IPMSM的实际凸极性吻合。另一方面，注入电压为 0.2Udc时In的幅值已经足够清晰，说明该电压幅值-频率比配置已能满足转子位置估计的需求。由此可见，通过采用本文的凸极信号测量方法，可为注入高频电压的幅值-频率比配置提供指导。

图轴高频电流幅值频谱分布

由频谱分析结果可见，频率为2fe=20 Hz的信号强度几乎可视为唯一的信号成分，其余频谱的谐波成分强度基本可以忽略，由此说明电动机的谐波凸极较弱，基本可认为只含有单一的空间凸极性。

PMSM仅含有单一的空间凸极性对于实现高频脉振电压注入法转子转速与位置估计具有积极意义，按照前文测量结果将注入电压幅值设置为0.2Udc，对转子转速与位置进行估计。图11为电动机在200 r/min(0.09pu)工况的实验结果，其中图11(a)代表转子转速与转速误差，图11(b)转子位置与位置误差。由实验结果可见，估计转速与转子位置精度较高，说明所选电压幅值-频率比配置能满足转子位置估计的需求，而且二者均不含有谐波成分，证明被测IPMSM实现高频脉振电压注入法转子转速与位置估计的性能较好。

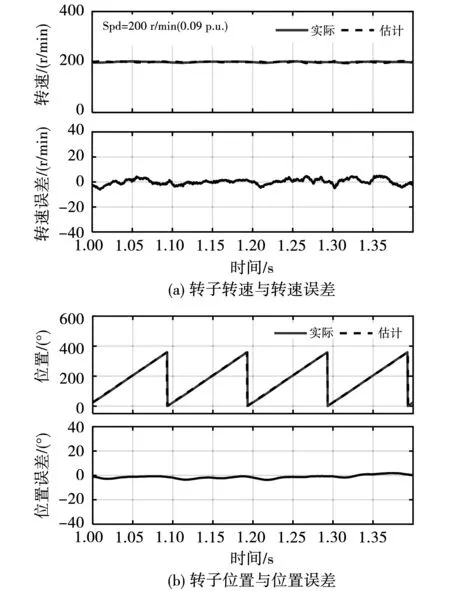
图11 电动机在200 r/min(0.09pu)工况的实验结果

4.2 #2号SPMSM凸极性测量及分析

同样地，在相同的测试条件下，对#2号SPMSM的凸极性进行测量。图12为2#SPMSM电流圆实验测量结果。图12(a)与图12(b)中，电动机转速为5 r/min(0.01pu)，二者注入的高频电压幅值分别为0.2Udc与0.3Udc；图12(c)与图12(d)中，电动机转速为40 r/min(0.08pu)，二者注入的高频电压幅值分别为0.2Udc与0.3Udc。

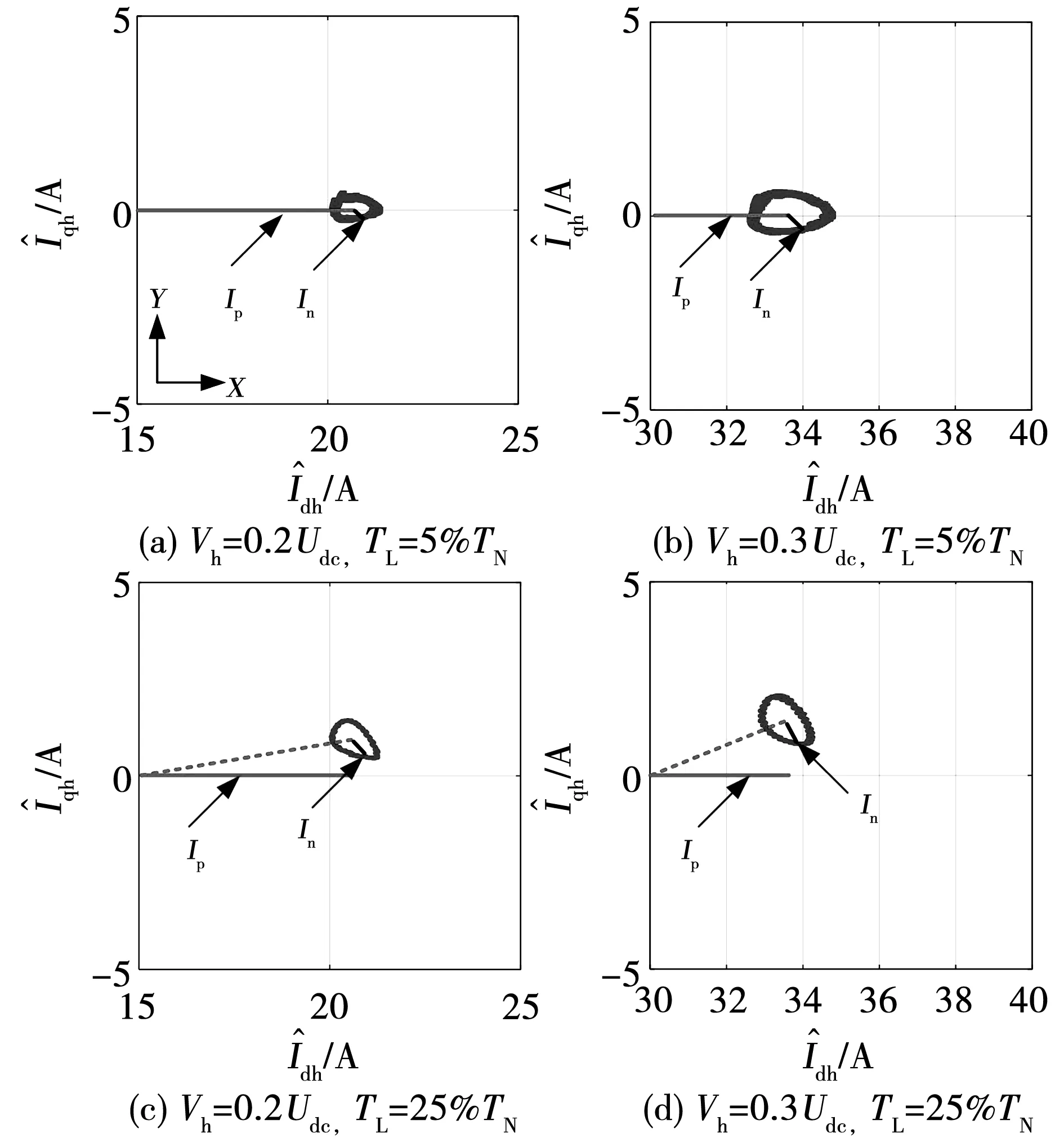
图12 不同转速工况下的电流圆实验结果(#2 SPMSM)

由实验结果可以看出，被测SPMSM具有一定凸极性，且注入电压幅值为0.2Udc时In已经能够清晰辨认，因此该SPMSM可利用高频电压注入法实现转子转速与位置估计。但是，电流圆畸变程度较为严重，说明电流幅值中存在较强的谐波成分，被测电机存在多凸极效应。在本文的实验平台中，转矩电流随电动机转速上升而增大。由图12(c)与图12(d)实验结果可以看出，随着转速升高(即转矩电流增大)，电流圆出现偏心现象，引起该现象的凸极称为静止凸极[17-18]。静止凸极与谐波凸极不同，为直流成分，其仅引起电流圆偏心。本文将偏心圆与Y轴0刻度水平线的夹角称为静凸极角θss，θss越大说明静凸极越强。在一定的高频电压-频率比配置下，利用本文所提的凸极信号测量方法，可以获悉静止凸极出现的临界转矩电流(被测SPMSM的临界转矩电流约为额定电流的5%)。

为了消除静止凸极的影响，可采取两种思路。一方面，使用高频电压注入法时将转矩电流控制在临界电流以内，可避免静止凸极的出现，这对优化电机调速性能具有一定实际工程意义；另一方面，可测量不同负载工况下静止凸极的强度以重构静止凸极，然后使位置误差信号与重构静止凸极信号相减，从而实现静止凸极彻底解耦。

(13)

式中：In0、φ0分别代表静凸极的幅值与相位；In4、φ4分别代表谐波凸极的幅值与相位。

图轴高频电流幅值频谱分析结果

图14展示了被测SPMSM在20 r/min(0.04pu)工况的实验结果，其中图14(a)代表转子转速与转速误差，图14(b)代表转子位置与位置误差。由实验结果可以看出，由于多凸极效应电动机的估计位置与转速出现明显波动，严重降低无位置传感器控制系统的控制性能。电动机的多凸极效应使位置估计产生误差，且误差随转子位置改变而改变，从而对转子位置估计精度、位置观测器带宽、电动机运行效率产生负面影响，严重时甚至引起转子位置估计失败。

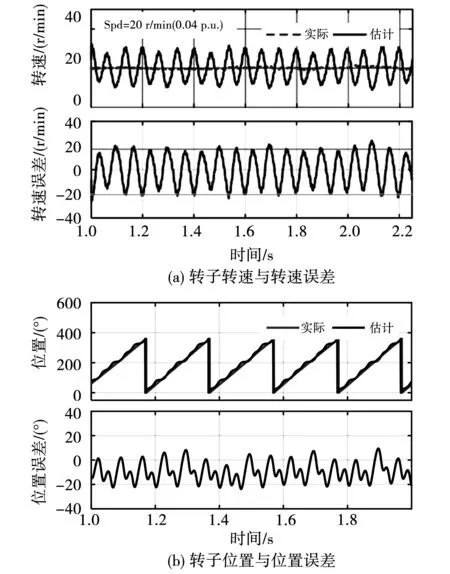
图14 电动机在20 r/min(0.04pu)工况的实验结果

综合图13与图 14的实验结果可知，采用本文所提电动机凸极信号测量方法，对位置误差信号进行频谱分析，可测定被测SPMSM的谐波凸极频谱，便于有针对性地消除谐波凸极。电动机多凸极效应的消除方法通常可以采用凸极性重构解耦法[14,21]、自适应解耦法[15]、非线性观测器[17]以及多高频电压信号注入解耦法[18]等等。由于电动机多凸极效应的消除不在本文的研究范围内，因此不展开讨论。

图15为#2号SPMSM负载工况下高频响应电流幅值与转子位置实验结果，其中图15(a)转速为20 r/min(0.04pu)，图 15(b)转速为40 r/min(0.08pu)。由实验结果可见随着转速提高(转矩电流上升)交叉饱和角θm不再为零，根据该角度关系可测量不同负载工况下的交叉饱和角。实际应用时，可将测量所得θm与电流关系制成数据表，然后在控制器中实时对转子位置估计误差进行补偿。

图15 #2号SPMSM电机负载工况下高频响应电流幅值与转子位置实验结果

5 结 论

传统永磁同步电机凸极性测量方法存在测试成本高、大功率场合不适用、信号分析过程不完整等不足。本文提出了一种基于高频脉振电压注入法的永磁同步电机凸极信号测量方法。采用所提方法分别在一台IPMSM与SPMSM上进行凸极性测量及分析，实验表明被测IPMSM的次凸极强度较弱，采用高频脉振电压注法时具有良好的转子位置估计性能。相反，被测SPMSM存在静止凸极与4次谐波凸极，转速与位置估计结果波动较为突出。

所提方法在电动机旋转过程中完成凸极信号测量，无需采用任何固定结构，可适用于不同功率等级的电机驱动平台。不仅有效降低实验测试的难度与成本，提高了方法的工程适用性，而且有助于改善高频电压注入转子位置估计方法在永磁同步电机驱动系统的应用、调试以及优化效果。