齐次化联立解决高考中与斜率和积有关的定点问题
廉换霞,林新潮
(福建省莆田第一中学,福建莆田,351100)
平面解析几何是用代数的方法研究它们的几何性质,体现了形与数的结合,重点提升学生的直观想象、数学运算、数学建模、逻辑推理和数学抽象素养,可见其重要性.所以,在每年高考全国卷的六道解答题中必有一道是解析几何.近几年高考中,常出现以斜率和或积为定值来探究直线过定点的问题.本文以三道高考题为例进行分析,并用齐次化联立的方法进行解答,以寻求此类问题统一的解决方法和思路.

(1) 求椭圆C的方程;
(2) 设直线l不经过P2点且与C相交于A,B两点,若直线P2A,P2B的斜率之和为-1,证明:直线l过定点.
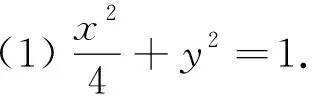
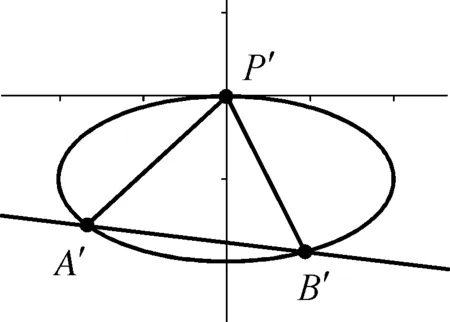
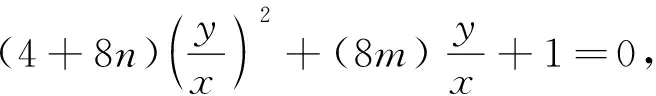
评注:本题利用齐次化联立来求解,相对于常规解法,大大减少了计算量,且具有模式化的解答过程,可以提升学生的直观想象、数学运算、数学建模素养.这里充分利用了直线经过平移不改变斜率的特性.本题的特点是有圆锥曲线上一定点P2,若两直线P2A,P2B的斜率和为定值,则直线AB过定点.那么有无更一般的结论呢?具体可参考林炳宗[1]等人的论文.该几何模型的特点是有圆锥曲线上一定点,两直线的斜率和或积为定值与直线过定点的等价关系.
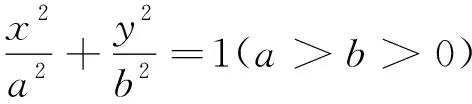
(1) 当a2d-b2≠0时,

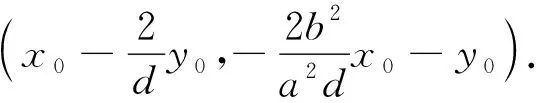

(1) 求C的方程:
(2) 点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
思路分析:本题已知AM⊥AN,我们可将几何关系代数化为kAM·kAN=-1.从而有椭圆上一定点(A),两直线(AM,AN)的斜率积为定值,符合我们研究的几何模型,解题思路就为推证直线MN过定点,并求出定点P坐标,又AD⊥DP,所以D在以AP为直径的圆上,得点Q为圆心,|DQ|为圆的半径.

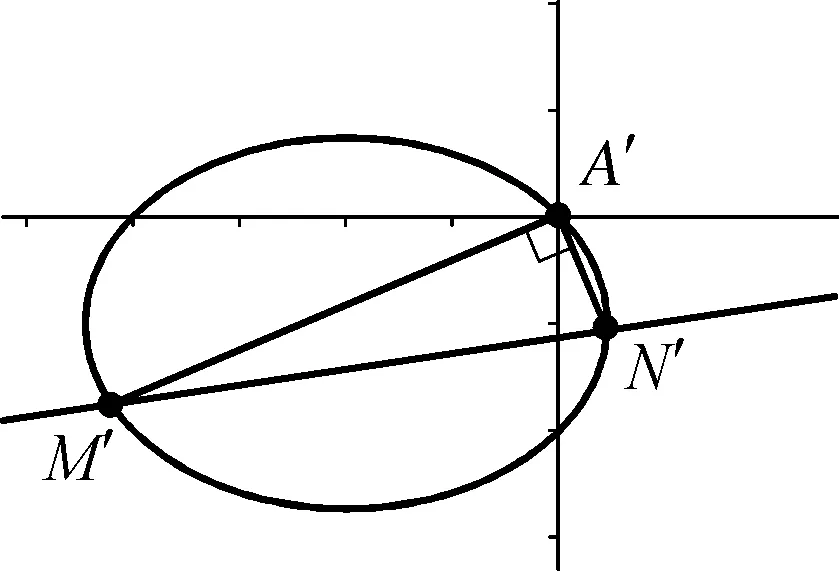
即x2+2y2+4x+4y=0,点A、M、N平移后为A′(0,0),M′,N′.直线M′N′不经过原点,可设其方程为mx+ny=1,代入椭圆方程有x2+2y2+(4x+4y)(mx+ny)=0即(1+4m)x2+(2+4n)y2+4(m+n)xy=0.
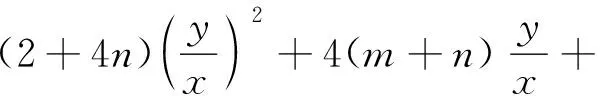

所以圆锥曲线平移后所得方程,对“x”是“左加右减”,对“y”是“下加上减”.

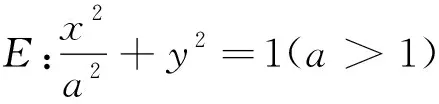
(1) 求E的方程;
(2) 证明:直线CD过定点.
思路分析:点C在椭圆上,A,B为左右顶点,由椭圆第三定义,可得所以我们连接BC,从而有椭圆上一定点B,考虑两直线BC,BD的斜率积是否为定值.惊喜地发现kPB=3kPA,通过kCA桥梁关系,可得BC与BD的斜率积为定值,符合我们研究的几何模型,进而推证直线CD过定点.

(2) 证明:点P在定直线x=6上,可设P(6,y0) .
又A,B为x轴上定点,A(-3,0),B(3,0)
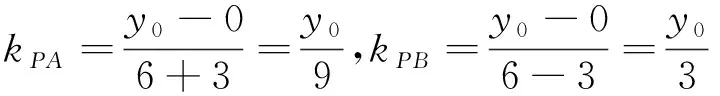
点C在椭圆上,A,B为左右顶点,有
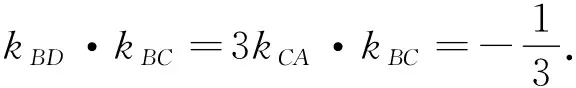
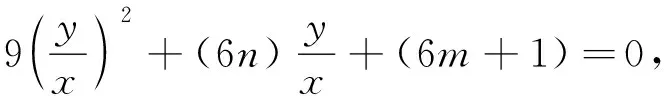
评注:此种解题方法在于,先去思考是否符合我们的几何模型,可以提升学生的逻辑推理和数学抽象素养.以后在我们解答圆锥曲线定点问题时,可以考虑先找曲线上一定点,若由其出发的两直线的斜率和或积为定值,则可按此模型推证直线过定点,为广大考生提供一种解题的思路.

