多法归一：厘清本质，感悟思想——一道例题的教学感悟

蒋志勇

(江苏省如皋初级中学，江苏如皋，226599)

数学思想是学生分析和解决一些综合性较强的数学问题的重要工具，在学生四能发展中起到十分重要的作用.数学教学，要重视数学思想的教学.一线课堂应努力将数学思想的发现与应用融入常态课堂，要力求让学生经历分析问题和解决问题的完整过程，并通过交流总结，感悟数学思想的客观存在和应用价值，从而提升其数学能力.本文拟结合一道例题的教学过程及简要分析，谈谈笔者的做法，供大家参考.

1 例题及分析

例题已知P=x2+t，Q=2x，若对于任意的实数x，P>Q始终成立，则t的取值范围为.

简析：本题是有两个等式和一个不等式组成的“求取值范围”的例题，题目将函数、方程、不等式等知识融为一体，意在让学生通过方程、不等式向函数的转化，调用函数思想、数形结合思想来分析和解决问题.本题被教师作为例题，安排在“二次函数的图象和性质”复习课中.

2 教学过程及简析

2.1 教学过程简述

2.1.1 自主解答，组内交流

教师投影例题，让学生自主解答，3分钟后，学生在学习小组中交流结果，解题思路及出错的原因.

2.1.2 全班交流，分享解法

学生组内交流结束后，教师安排学生进行了8分钟的解法分享，按小组分别展示了如下几种解法：

小组1：P=x2+t，Q=2x，可以看作是两个关于x的函数，P>Q就可以看作是函数P的值的大于函数Q的值，接下来在坐标系中作出两个函数的大致图象.如图1，当两函数图象只有唯一的一个公共点时，P=Q，此时，方程x2+t=2x有两个相等的实数根，Δ=0，所以，t=1，将P=x2+t的图象向上平移，即让t>1，即可保证P>Q了.

小组2：由P>Q得P-Q>0，将P=x2+t，Q=2x统整为一个函数y=x2-2x+t，作大致图象如图2，结合P-Q>0得y>0，即函数图象位于x轴上方，所以，方程x2-2x+t=0有两个不相等的实数根，所以，由Δ>0可得t>1.

小组3：P>Q，即x2+t>2x，整理得x2-2x>-t.令y1=x2-2x，y2=-t，作两函数的图象如图3.当y2=-t的图象位于y1=x2-2x的下方时，满足题目要求，此时-t<-1，即t>1.

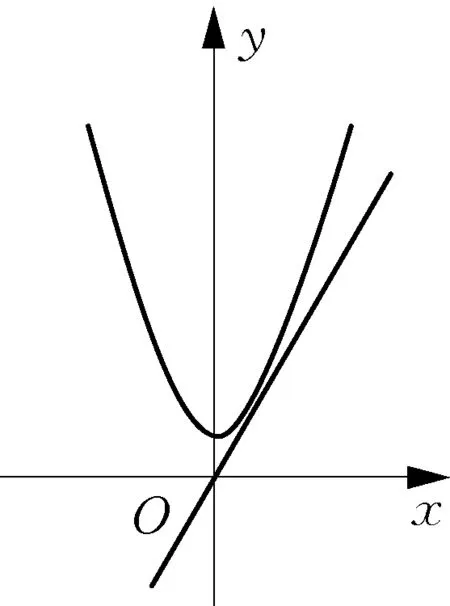
图1

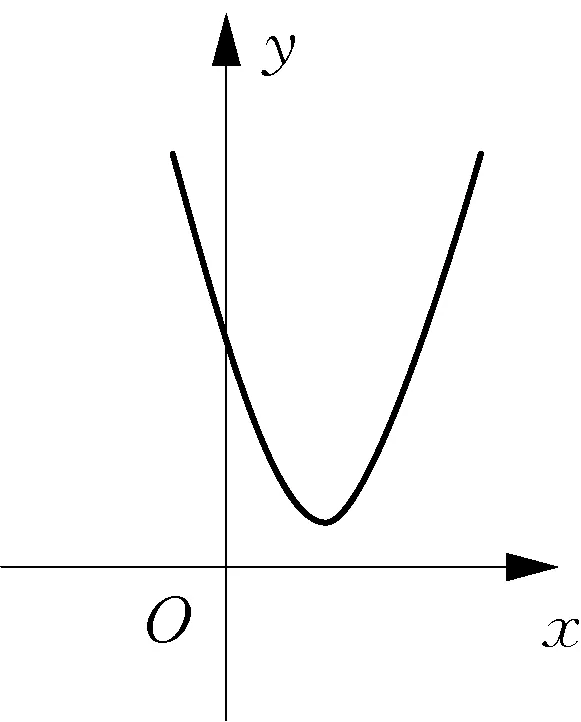
图2

图3

2.1.3 小结提升，归纳经验

教师引导学生回看三个小组列出的式子、画出的图象，逐一梳理三种不同解法的解题过程，并归纳出共性过程：先依据题意建构数学模型(数)——一次函数或二次函数，画出函数图象(形)，根据函数图象建构新的方程(组)或不等式(组)等数学模型(数)，通过解这些新建的模型得到问题的答案.教师随即将“数→形→数”板书在黑板上，并指出这是今后解答此类数学问题的一般路径.

2.2 简析

教师为这道例题的教学安排了三个环节：第一环节，自主解答，组内交流.学生先独立思考，尝试解决问题，然后小组交流，各人将自己的思考成果组内分享，并在小组中达成共识；第二个环节，全班交流，分享解法.教师安排学生以小组为单位将本组的解法再全部进行了分享，三种不同路径下的数形结合，为下面的总结归纳提供了充足的素材；第三环节，小结提升，归纳经验.教师引导学生围绕第三个环节中呈现的三种不同方法，归纳其共性路径，学生在梳理中不断感悟数形结合思想，并对解决此类问题的一般方法——“数→形→数”有了更深的认识.

3 教后反思

3.1 例题教学要关注问题本质

例题教学要关注问题的本质，要带领学生揭去问题情境的外衣，透过现象看本质，把握问题的实质，从而找寻到问题解决的一般路径.比如，本文中的这道例题，表面看是方程、不等式，其实质确是函数问题，是需要借助函数图象的高低来解决的.在教学中，如果教师不去引导学生透过方程组、不等式这一表象，去看到函数的本质，那问题的解答与交流时很难有深度的，学生的发展自然也就很难契合例题设计的要求了.事实上，例题的本质在其作为例题时就已经明确了，比如，本文中的这道例题被教师安排在“二次函数的图象和性质”复习课上，其用意是十分明显的，如果学生个体不能看透这个话，片断中安排的小组交流、全班交流同样可以揭示这一实质，所以，关注例题的本质应是教师课前要做的功课，课上也可以在适当的时机予以明晰.

3.2 解题交流要聚焦同质方法

一题多解在数学中十分常见.相同的数学问题，不同人会有不同思考路径，也就会产生不同的解题方法.人的差异、情境的不同等都是产生异样解法的重要原因，而我们的数学教学在通过多样解法呈现学生的不同思维历程，达到梳理知识、积累经验的目的时，我们还应关注同质方法的归纳总结，要力求在相同解法的“同在何处”和“差在哪里”的详实分析，让学生获取这类数学问题解决的通解通法，以求实现“解一题，会一类，通一片”的教学目标.再来说说文中的这道例题，学生完全可以利用配方法来求解，但教师并没有将此为作为教学的重点加以呈现，而是让学生观摩了三组“数→形→数”的求解过程，这些同质方法的交流，使学生对方程(组)、不等式(组)与函数的关系，函数的解析式法与图象法的关系有了深刻的认识，有助于他们厘清初中最常见的三种代数模型之间的关系.

3.3 思想感悟要扎根过程体验

数学思想教学，过程体验尤为重要.数学思想一般都是隐性存在的，没有个体的深入体验，我们一般很难发现数学思想的客观存在.因而，数学思想教学，要重视过程的历练，要让学生在近乎相同的分析问题和解决问题的过程中，不断感知到同一类型路径在问题解决过程中的价值.此时，再辅以教师或学生的适时点拨提升，数学思想才会“跃然纸上”，成为学生能够接受的数学现实.以本文所涉及的数形结合为例，我们平时教学一直挂在嘴边，本节课上如果没有每一名学生自主的过程探索，没有小组交流的分享探讨，没有全班交流的图文展示，学生对“数→形→数”的过程体验绝不会有本课中的那样深刻，对数形结合思想的认识也不可能达到本节课教学的高度.

例题教学，是数学教学的重要任务.面对同一道例题，不同的老师讲评会有不同的侧重，有些老师注重一题多解，有些老师注重思路分享，有些老师注重过程展示……本文中的老师则做到了多法归一，在众多同质方法中抽取了共性方法——数形结合.这样的教学，源于例题，但高于例题，将解题通法作为教学的核心任务，在方法归纳中引领学生感悟数学思想，给例题教学设置了“立足当下，放眼长远”的目标定位，从教学成效看，如此教法，还是可取的.以上是笔者基于一道例题“多法归一”教法的点滴思考，因才疏学浅，疏漏之处难有，敬请各位同行专家批评指正.