促进数学习题课教学有效性的实践与思考

张 晨

(南京市第九中学，江苏南京，210000)

1 数学习题课教学现状

现阶段，不少中小学老师仍然习惯将过去的“题海战术”作为指导数学的教学规律和高考应试训练的法宝，因为他们始终坚信“熟能生巧”.但是过度的练习只会让学生“熟能生厌”，使学生不想学习，阻碍其发展.在这种比较传统枯燥的高中数学的教学训练方式下，学生虽然能够较迅速快捷地理解识别考试题型、套用各种解题策略的思维技巧方式和学习方法，但是对于应用普通数学知识工具去直接解决现实生活场景中遇到的某些实际的问题时，他们往往变得束手无策.最终会导致许多学生只能停留在机械模仿的层面上进行解题，不利于学生的思维能力、创新意识及应用能力的培养和提高，从而使素质教育很难真正落实.

通过对多年实验研究探索后发现，在陈旧落后的学校，传统的数学习题课业测验及教学评价思维模式体系中加入一些富有启发性、开放性、探究性问题，可以在很大程度上，有效弥补学校在传统的数学纸、笔、题、作业等测验考查形式框架中的封闭性，试题体系固有存在的种种教学功能及不足，从而提高数学习题课的教学有效性.在进行高中数学新课程实验教学研究工作中，教师发现：如若教师们能及时系统地按现行考试指导大纲要求，结合现有高中阶段通用各种版本教材，经常针对性地和适时而定量性地去对其教材某些基础定理、例题等一一去作比较，进行认真地、详细地、系统地和透彻地剖析，编拟好其中一些题目难度系数适中、形式十分活泼和多样新颖的且都十分能吸引学生思考特点的开放性、探究性题目，让学生开动脑筋去探究及思考，这将会对提高课堂教学气氛、激发培养起学生课外自主学习与探究的兴趣、培养并提高学生课外自主思维创造技能及创造思维能力等会起到一个十分正面、积极的作用，使数学习题课真正体现课程改革的理念.

2 开放性问题

开放性问题，是指一个相对较于一般那些考查条件较完备、结论相对确定可靠的封闭式研究问题类型而言，在具体设问和方式研究上也要求具有多角度、多层次研究的开放型问题.开放性数学问题，或条件结论均不完全唯一，或已知条件皆不十分完备，或未知条件和未知结论都比较开放，彻底上改变了中国传统开放性数学题思维的一种封闭的形式，容易充分激发了学生思维探求的欲望，诱导着学生主动离弃他们原有固定的传统思维轨道，从不同学科的认知角度、寻求以不同思维的途径去解决这些问题，为新世纪学生个性化的开放数学问题学习的活动探索创造提供了另外一种充满探索未知、富有探索挑战意识的思维新的环境，让开放式数学的学习活动真正成为了一个生动的、主动参与的、个性表达的学习过程.

2.1 设计结论开放性问题

例1已知定义在R上的函数f(x)不是常值函数，满足以下两个条件：①f(1+x)=f(1-x)；②对任意x1∈R，均存在x2∈R使得f(x1)=2f(x2)成立；则函数f(x)=.(写出一个符合条件的答案即可)

本题条件中仅给出了函数满足的两个性质，需要学生根据性质，写出符合条件的一个函数.要求学生对于函数的对称性和取值范围有比较深刻的认识，能够灵活的使用.

2.2 设计条件开放性问题

例2设数列{an}的前n项和为Sn，，若bn=an·2an，求数列{bn}的前n项和.请在以下三个条件中任选一个，补充在上面的问题中，并进行解答.

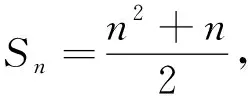
本题在推导an的通项公式时，学生可以自由选择，可以选择an与Sn的关系，可以选择an的相邻项之间的关系(差的关系，或者是商的关系).而这几种得到通项公式的方法，都是学习过程中的重点内容，学生可以根据自身具体情况，选择最擅长的方法进行求解.

2.3 设计条件和结论都开放性问题

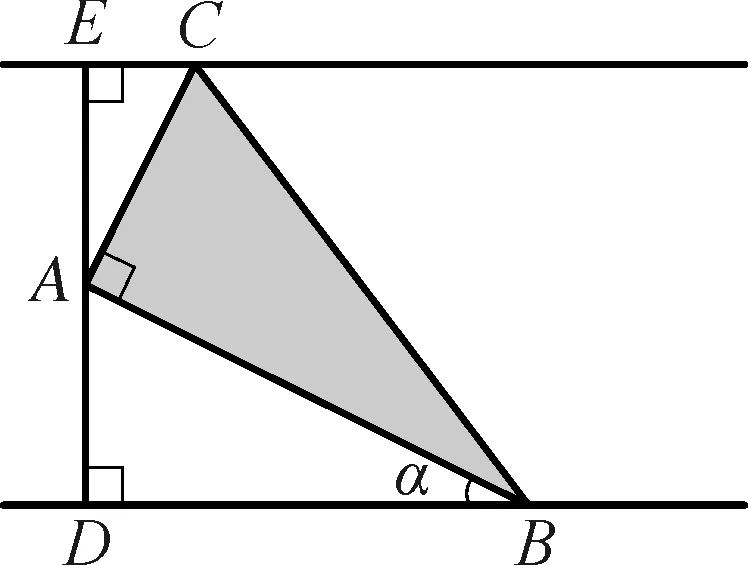
例3如图，某公园内有一条宽为100米的笔直的河道(假设河道足够长)，现拟在河道内围出一块直角三角形区域养殖观赏鱼.三角形区域记为△ABC，A到河两岸的距离AE,AD相等，B,C分别在两岸上，AB⊥AC.为方便游客观赏，拟围绕△ABC区域在水面搭建景观桥.为了使观景桥的总长度L(即△ABC的周长)最短，工程师设计了以下两种方案，请从中自选一种解答.

方案1：设∠ABD=α，求出L关于α的函数解析式f(α)，并求出f(α)的最小值.

方案2：设EC=x米，求出L关于x的函数解析式g(x)，并求出g(x)的最小值.

在解三角形问题中，用角表示和用边表示三角形中的边角关系，本身就是非常重要的两种思考问题的角度.本题以开放的形式，让学生自己选择研究的角度，是用边表示，还是用角表示？是用正弦关系，还是用余弦关系？

开放题的条件可以是一般性的规则，也可以是一段材料，常常在细微之处体现编题的功夫.开放题的解答和编制过程，是建构认知的全过程，能充分体现答题人或编题人的能力，这不是由套路可以直接办到的.因此，编制开放题的要求和难度要大于编制其他题.作为教师，要在习题课的教学中充分发挥其作用，让各类题目取得匹配作用和综合效应，进而最大可能地发挥数学题的教学作用，实现数学习题具有的最大数学教育价值，以此提高数学习题课的教学有效性.

3 探究性问题

探究性问题是指给学生提供一定的数学事实，要求学生归纳、探索出一定的数学结果.它的主要特点在于条件和结论有可能都是需要自己去发现的，有时还不是唯一的.这一类综合试题解法的合理求解过程应更加富于思维创造性，有助于真正调动高三学生复习的主观学习与积极性，激发高考学生良好的自主求知欲力和学习进取创新精神.

3.1 给出题设条件，但结论未指明，或者只给出结论范围，但要求解题者作出判断或选择

例4设函数f(x)对于x,y∈R都有f(x+y)=f(x)+f(y)，且x>0时，f(x)<0,f(1)=-2.

(1) 说明函数f(x)是奇函数还是偶函数？

(2) 探究f(x)在[-3， 3]上是否有最值？若有，请求出最值，若没有，说明理由.

本题的第(2)问要探究函数f(x)在区间上的最值，前提是学生先能主动发现函数f(x)自身具备单调性和奇偶性，在应用这两项性质的基础之上，再去进一步研究函数的最值问题.所以需要学生对于函数的一般性质有一定的研究基础，给自己后面的研究寻找一些必要的台阶.

3.2 给出题目结论，但没有给出或部分给出题目的条件，要求给出或补充使题目成立的条件

例5已知函数f(x)=e2x-8ex+6x，若曲线y=f(x)在点P(x0，f(x0))处的切线与该曲线有且只有一个公共点P，则以下选项中满足条件的x0可以是( )

A. -ln 2 B. ln 2 C. ln 4 D. ln 5

本题中给出了最后需要满足的结论，学生可以通过结论反过来推出满足条件的x0需要满足的范围，从而进行选择.也可以将四个选项中的x0依次代入条件，正面研究此时是否符合最后的结论.正向思维和逆向思维，都是数学学习过程中需要培养的思维方式，学生可以通过这种方式进行自主的强化.

3.3 给出了一些特殊的情况，要求考生归纳、猜测这些一般情况结论并最后给出证明

例6设fk(x)=sin2kx+cos2kx(x∈R)，

(1) 求fk(x)在k=1, 2, 3时的值域；

(2) 猜想k∈N*时fk(x)的值域(结果用k表示)；

(3) 对于(2)中的值域的结论，试用二项式定理给出证明.

本题需要学生细心观察k=1， 2， 3时的三个结果，大胆猜测k∈N*时fk(x)的值域，要求学生具备很强的归纳推理的能力.而后面的证明过程，则需要结合二项式定理中的相关结论.“大胆猜测，小心求证”本身就是数学学科发展的主要途径，因此从这个方面给予学生一定的探究指导，对于其后续的成长发展都是有好处的.

4 展望

数学基础教育，是一门着重关注如何培养高中生数学思维模式与能力的教育学科，有效且扎实深入地推进高中数学基础阶段教学，更应该着重注意让学生们在能够学到掌握一定高中数学知识方法规律的同时，渗透学习数学思维方式，数学思想与现代基本生活数学观念.

新课程实践教学过程强调高效课堂，有效教学，而对如何去提高整个高中数学课程实践教学过程工作质量，又更需要在我们最大程度去发挥有效课堂劳动；有效教学过程辅助教学功能发挥效率与作用，减少由于课堂无效教学与无效的课堂互动之间所造成的时间浪费，减轻了高中学生对课外的学习与劳动时间的无谓紧张和强度，提高了有效的课堂与有效的教学之间的总体效率，达成基础教育新课程整体育人水平的总目标.在中学数学习题课中，如能合理地加入一些有利于培养与考查学生创新意识、创新思维和应用能力的开放性问题、探究性问题，则可以更好地提高习题课的教学有效性，真正关注学生自身的各项能力发展，从而更好地培养学生的探索精神和创造能力.

有效科学的教学理念能够真正激活沉睡多年的潜能，开启被封存起来的记忆.教学无止境，在新课程教学的道路上我们还有很多方面需要去探索和实践.