深入问题本质 激活学生思维

兰诗全

(福建省古田县第一中学，福建宁德，352200)

数学问题本质，就是数学知识内在的根本属性与规律，蕴含数学思维特点，数学思想方法.数学高考题每年都在变，但它对数学本质和思想方法的考查却始终不变，为此教师在教学中要“以不变应万变”，积极引导学生揭示数学本质，理解数学本质，反思数学本质，让学生有一双透过现象看本质的慧眼，只有引导学生把握数学本质，才能避免 “不识庐山真面目，只缘身在此山中”的迷惘，才会“识破天机，豁然开朗”，充分体会蕴含其中的数学思想方法，使学生的数学核心素养得到充分的发展.如何深入数学问题本质，激活学生思维？以下结合例子谈“三点”做法，以期抛砖引玉.

1 一题多解深入本质激活思维

当你找到一个数学问题的答案后千不可就此了结，要多问问到底解释问题本质了吗？本题的真正意义是什么？有没有更好的方法？著名的数学教育家波利亚曾形象地指出：“好问题同某种蘑菇有些相像，它们大多成堆地生长，找到一个以后你应当在周围再找一找，很可能附近就有好几个.”数学问题的解往往也是如此.

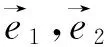
分析：这道题构思匠心独具，命题角度新颖，内涵丰富深刻，不仅有数表达的简洁，还充满了“形”的神韵，堪称经典.思维灵活多样，方法有繁有简，具有相当好的区分度，理解越深入，本质越揭示，方法越简单.若只想数未“见”形，也有以下方法如法1、2.但相对计算方法要更扎实，若发现向量几何意义，数形交融，就能“见”形，才会渐渐深入问题的本质，解法也就会越来越简洁明了.

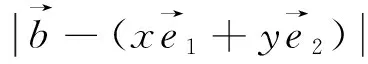
=x2+(y-4)x+y2-5y+b2

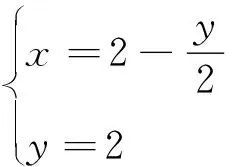
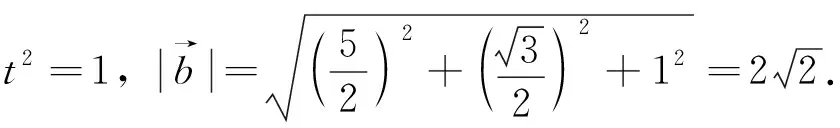
以上纯代数方法计算，未充分揭示问题本质.华罗庚说：“数缺形时少直观，形离数时难入微，数形结合百般好，数形分离万事休.”本题具有很好的数形结合教学的功能.

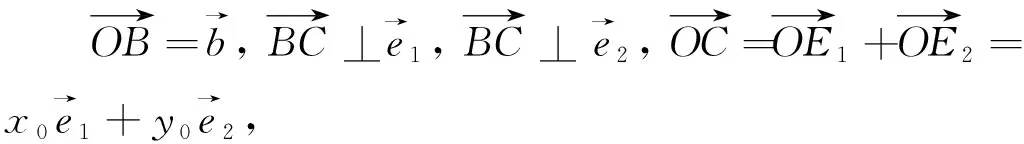
BM⊥OM，BN⊥ON，则CM⊥OM，CN⊥ON.

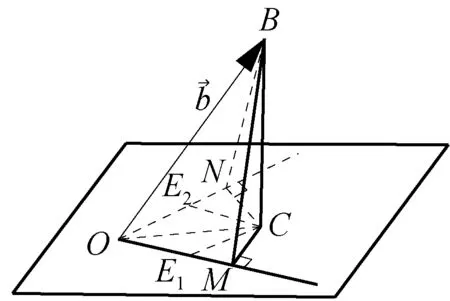
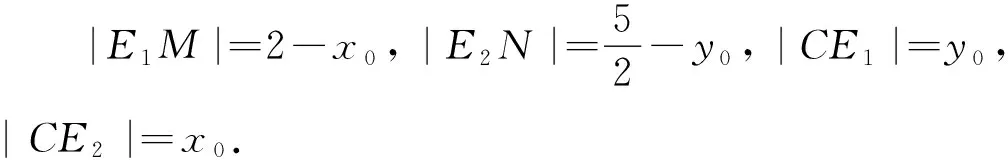
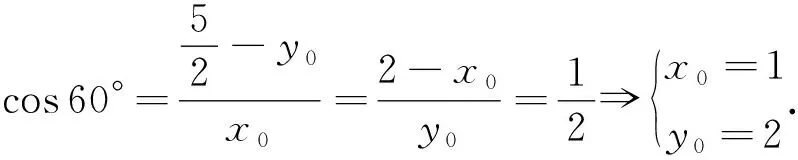
以上方法虽不算最好，但已解开“数形结合”的面纱，初步体现了数与形的关系，进一步揭开问题的本质，还有以下方法.

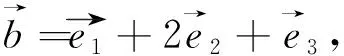
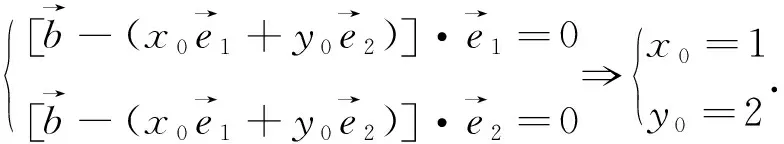
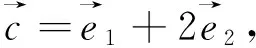
解法4、5透过数揭示形，形数结合，简洁明了，突出本质，沟通数学内部多层次的联系，彰显数学力量与数学之美，有效提高数学解题教学的本真意义.还有更好的方法吗？读者好好想想.

数学家加德纳说，数学的真谛在于不断寻求越来越简单的方法.证明定理和解决数学问题以及解答这个问题的思维过程应是自然的、简单的，所用的知识是基础的.大道至简，师法自然，数学是自然的，数学是清楚的，用最简单的方法说明最深刻的道理才是数学之精髓.

2 正误辨析深入本质激活思维

在数学教学过程中，经常会发现学生在解题中犯下各种各样的错误，许多教师和学生往往只简单地归结为“马虎”“不认真”所致，轻描淡写地提醒下次注意就过去了，可是到下次解题时又重复“昨天的故事”，缺少对错误问题的深思考.从一定意义上讲，“错误问题”比“正确问题”更有教学价值，教师要好好利用这难得的教学资源.

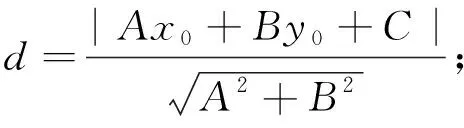
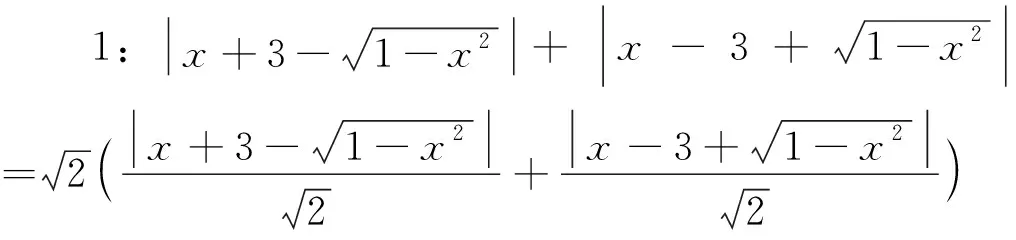
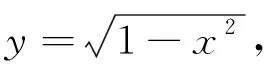
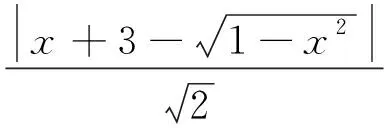
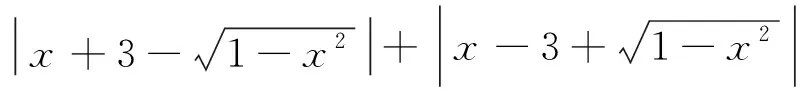
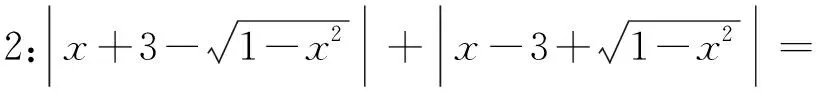
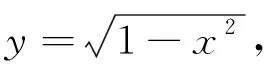
思考：以上解法根据充分吗？师生进行问题的再认识再思考后又可得出以下说理清楚的解法.

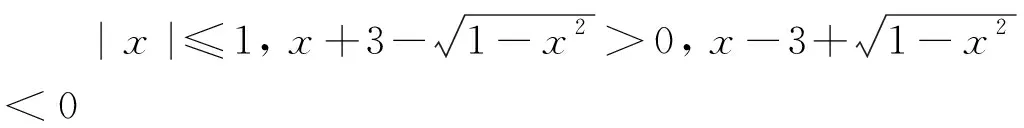
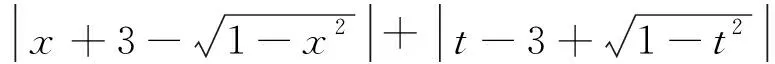
以上教师借助“错误问题”将教学深入本质，激发思考，帮助学生解决了困惑，完成了心愿，使学生的求知欲、探索欲、表现欲、创新欲得到了满足，并获得了富有个性的学习感悟.过程虽曲折，印象很深刻，收获已满满，在悟错中深入问题本质激活学生思维，取得了出人意料的教学效果.

3 变式问题深入本质激活思维

变式问题有它的独特功效，它能深入本质，激活思维；它可用较少的时间使学生将所学的知识条理化、系统化、网络化，又能培养学生的思维能力，提高解决问题的应变能力，还能调动学生参与解决问题的热情，大大提高课堂教学的效率.

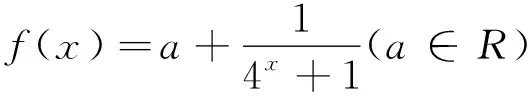
解法1：利用奇函数定义f(-x)=-f(x).

解法2：利用奇函数f(0)=0，再检验之.

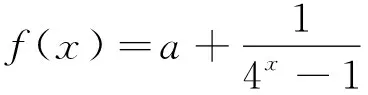
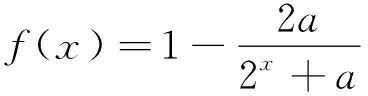
如变式1中f(0)没有意义，怎么办？变式2中有何切合本题的好方法，变式3中直接用f(0)=0求解，得a=1，但漏掉a=-1.为什么？通过变式数学问题，激活学生思维，展开积极的思考，让学生对问题的认识不断走向深刻本质.

数学就其本质而言是一种思维，数学课堂的根本就是培养和发展学生的数学思维能力.通过变式问题教学，力求做到思维迁移具有深刻性、发展性和创造性，变式训练具有拓展性、探索性和灵活性，教学紧扣学生的心弦，使得课堂充满生机与活力.

苏霍姆林斯基说：“在人的心灵深处都有一种根深蒂固的需要，这就是希望感到自己是一个发现者、研究者、探索者.”学生对问题的好奇心和探知欲是天生的，关键是教师如何让学生在课堂上能主动提出问题，深入问题本质，激活学生思维，让学生在参与中学习，在体验中感悟，在实践中提升，切实提升学生数学学科素养.