基于模体的朴素贝叶斯链路预测方法
曾茜,韩华,马媛媛
(武汉理工大学 理学院,武汉 430070)
0 概述
随着网络科学的不断发展,在社会科学、自然科学、信息科学等领域中的复杂关系问题都可以通过复杂网络来描述[1]。在复杂网络中通常出现网络未知或部分未知的情况,因此,对缺失信息的还原和预测是网络研究过程的关键。链路预测是根据已知的网络信息,预测尚未形成连边的两个节点之间产生链接的可能性,以预测未知链接[2]和未来链接[3]。链路预测被广泛应用在不同领域中,例如,在蛋白质网络中探究蛋白质之间的相互作用[4-5],在电商网络中推送客户感兴趣的产品[6],在社交网络中推荐可能认识的人[7],在航空网络中推测影响网络演化的重要因素[8]等。
现有链路预测方法从结构相似性[9]角度可以分为基于局部结构的方法(如共邻节点指标(CN)[10]、Adamic-Adar(AA)[11]、资源分配指标(RA)[12]等)、基于半局部结构的方法(如局部路径指标(LP)[13])和基于全部结构的方法(如考虑全局路径的Katz 指标[14]、节点偏好性随机游走指标(DRW)[15])。基于局部结构的方法因计算复杂度低、适用性广等优点备受研究人员的关注[16],但这类方法大多简单地假设每个共邻节点对链路形成的贡献一致。为此,文献[17]提出局部朴素贝叶斯(LNB)模型,引入朴素贝叶斯理论来区分不同共邻节点的贡献,取得了较优的预测效果。文献[18]提出树增广朴素贝叶斯预测(TAN)方法,引入树增强朴素贝叶斯概率模型,缓解在共邻节点之间强独立性假设的问题。文献[19]提出扩展局部朴素贝叶斯(ELNB)方法,通过对共邻节点的角色贡献函数进行扩展,揭示了微观尺度下节点聚类系数对链路形成的作用。但这些方法都是基于共邻节点的角色贡献展开研究,忽略了路径结构特征的贡献。近年来,已有研究表明,考虑路径结构周围的拓扑信息能有效提升预测性能[20-21]。
此外,LNB 模型及其相关改进方法并未考虑网络中的模体结构特征,而真实网络(如食物链网络、社交网络)存在大量模体结构。针对含有模体特征的网络,LNB 模型仍存在局限性问题。网络模体的概念最早由文献[22]提出,即在真实网络中富集出现的由少量节点形成的小规模同构子图。文献[23]提出模体顶点度和边度来衡量网络中点和边的重要性。文献[24]提出三角模体度和四边模体度的代数算法,设计基于模体特征的攻击策略。文献[25]依据朴素贝叶斯理论解释了使用模体边度进行链路预测的可行性,提出基于单模体边度和双模体边度的链路预测方法,揭示了模体对链路形成的重要作用。随着模体在复杂网络中深入研究,模体顶点度和边度已经不足以描述更复杂的拓扑特征,基于路径结构的模体测度量有待提出。
本文结合路径模体特征与朴素贝叶斯理论,提出一种基于模体的局部朴素贝叶斯链路预测方法MLNB,以分析路径结构的模体特征对节点相似性的影响。定义路径结构上三角模体的聚集程度——模体密度,考虑模体密度对待测连边的影响,通过构建路径的角色贡献函数分析路径的相似性贡献,同时推导出基于共邻节点的扩展指标。
1 基本概念
1.1 问题描述
本文给定一个无权无向网络G=(V,E),不考虑网络中的重边和自环,其中V和E分别表示网络中所有节点的集合和所有边的集合,全集U表示所有可能边的集合。exy∈E表示节点x和节点y存在连边,∉E表示节点x和节点y不相连。网络中节点总数为|V|=n,边的总数为|E|=m,最大可能的边的数量为|U|=。节点x的邻居集合用Γ(x)来表示,节点x和节点y的共邻节点集合表示为Γ(x,y)=Γ(x)∩Γ(y)。链路预测的目标是寻找集合U-E中缺失或暂未连接的边。
1.2 相关指标
在现有链路预测方法中常用的相似性指标主要有8 个:
1)共邻节点指标。对于待预测节点x和节点y,如果共邻节点个数越多,则x和y连边的可能性越大。通过节点对x和y的相似性得分计算它们共邻节点的个数,如式(1)所示:

2)Adamic-Adar指标。AA 指标考虑共邻节点的度越小对链路形成的贡献越大,在CN 指标的基础上为每个共邻节点分配一个权重,权值定义为该共邻节点度的对数的倒数。AA 指标定义如式(2)所示:

其中:kω为节点ω的度。
3)资源分配指标。对于未连接的节点x和节点y,在资源从节点x传递到节点y的过程中,每个共邻节点的资源传输量与其度值成反比。RA 指标定义如式(3)所示:

4)基于CN 指标的局部朴素贝叶斯相似性指标(LNBCN)。在CN 指标的基础上,LNBCN[17]考虑不同共邻节点对链路形成的贡献不同,定义了角色函数Rω来度量每个共邻节点的贡献,如式(4)所示:

其中:s为节点x和y相连的概率与不相连概率的比值。
5)基于AA 指标的局部朴素贝叶斯相似性指标(LNBAA)。将局部朴素贝叶斯原理与AA 指标相结合,LNBAA 定义如式(5)所示:
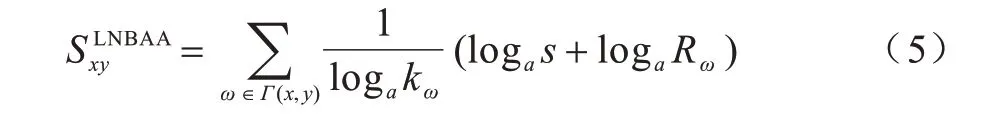
6)基于RA 指标的局部朴素贝叶斯相似性指标(LNBRA)。将局部朴素贝叶斯原理与RA 指标相结合,LNBRA 定义如式(6)所示:

7)局部路径指标。不同于上述6 种局部指标,LP 指标是一种半局部指标,不仅考虑了二阶路径(即共邻节点)的贡献,也考虑了三阶路径对节点相似性的贡献。LP 指标计算如式(7)所示:

其中:A为网络的邻接矩阵;A2和A3分别为待测节点对的二阶路径数和三阶路径数;α为控制三阶路径权重的可调参数,一般取值为0.01。
8)Katz 指标。全局相似性指标Katz 计算节点x和y之间所有路径的贡献,其定义如式(8)所示:

2 本文方法
2.1 模体理论
模体是一种介于节点和社团之间的网络子图,是在真实网络中频繁出现的结构单元,可以很好地反映网络的结构和功能。模体的基本特性是在真实网络中出现的频率远高于其在规模相同的随机网络中出现的频率。模体的基本统计特征如下:
1)模体的频率。对于给定的含有n个节点的子图M,如果子图M是网络的模体,那么模体M的频率[22]定义如式(9)所示:

其中:n(M)表示该子图在真实网络中出现的次数;N表示含有n个节点的子图出现的总次数。
2)模体的P值。模体M在随机网络中出现次数的频率大于节点数量相同的真实网络中出现次数的频率。P值越小,说明真实网络的模体特征越明显[22]。
3)模体的Z得分。对于模体Mi,Nreali表示该模体在真实网络中出现的次数,Nrandi表示该模体在随机网络中出现的次数。Nrandi的平均值为<Nrandi>,标准差为σrandi,则模体Mi在真实网络中的Z得分[22]如式(10)所示:

网络中模体的存在性可以根据上述模体概念和基本统计特征来检验。在大多数无向网络中,三节点模体是最常见的模体结构。三节点构成的两种模体结构如图1 所示。Δ 型三角模体作为网络中最小的完全图,构成网络中信息传播的局部单元,能反映网络局部结构中的聚集特性。本文基于网络的三角模体特征,提出针对三角模体结构的链路预测方法。
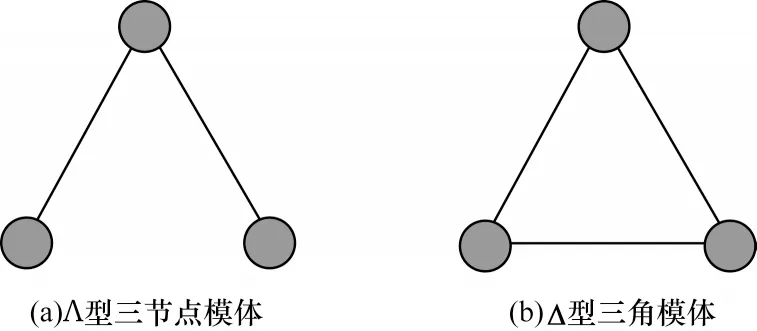
图1 在无向网络中三节点模体结构示例Fig.1 Examples of three-nodes motif structure in undirected network
2.2 模体密度的分析与量化
LNBCN 指标在CN 指标的基础上,区分每个共邻节点对待测连边的不同贡献,进一步提高预测精度,但忽略了经过不同共邻节点的路径对待测连边贡献的差异性。在路径上三角模体的聚集程度即模体密度,对待测节点间连边的产生具有重要影响。本文引入不同的局部结构图进行对比分析,3 种不同的节点连接方式如图2 所示。

图2 3 种不同的节点连接方式Fig.2 Three different node connection methods
从图2 可以看出,在3 种结构中均有一对待测节点x和y,以及待分析的路径结构wxωy。从图2(a)和图2(b)可以看出,节点x和节点y的度值都相同,3 个共邻节点的度值也都相同。但结构1 中路径wxωy的Λ 型模体都不构成Δ 型模体,例如。在结构2 的路径wxωy上Δ 型模体的聚集程度更高,这说明结构1 的路径wxωy对Λ 型模体形成Δ 型模体起到抑制作用,结构2 的路径wxωy对形成Δ 型模体有促进作用。对于三节点模体Λxωy,结构2 比结构1 形成三角模体Δxωy的可能性更大,即节点x和节点y产生连边的可能性更大。从图2(b)和图2(c)可以看出,3 个共邻节点既具有相同的度值,邻居之间的连边数也相同。根据LNBCN 原理,即用节点聚类系数来区分和量化不同共邻节点的贡献,由于在结构2 和结构3 中共邻节点ω的聚类系数相同,因此对待测边的贡献相同。从图2(c)可以看出,以节点ω为共邻节点的任意待测节点对,例如(v1,v2)和(v3,v5),节点ω对它们连边的贡献度都是相同的。LNBCN 方法仅考虑共邻节点本身的局部特征属性的差异化,却忽略了共邻节点与其待测节点之间连边的局部结构差异。在结构2 中路径wxωy上的Δ 型模体个数明显更多,模体聚集程度明显高于Λ 型模体,说明结构2 中路径wxωy对形成Δ 型模体Δx,ω,y的促进作用更大,节点x和节点y更有可能形成连边。在结构3 中3 对待预测节点(x,y)、(v1,v2)和(v3,v5),路径上的Δ 型模体聚集程度各不相同,分别对待测节点产生连边的影响程度也不相同,不能简单地用同一节点聚类系数来度量各自的贡献。此外,从信息传播路径的角度,共邻节点提供二阶传播路径,模体聚集程度越高的二阶路径结构也能提供更多的三阶传播路径,以图2(b)为例,三阶传播路径有,为节点x和y之间信息传播提供更大的可能性。
上述分析表明,节点x和y产生连边的可能性会因路径模体特征的不同而不同。因此,本文考虑到每条路径的模体特征对相似性有一定的影响,通过定义新的模体测度量来描述路径结构上模体的聚集程度。
在复杂网络中边聚类系数是刻画局部三角环聚集程度的重要参数。根据边聚类系数的定义,即一条边的两个端点与其共邻节点之间所构成的三角形数与所有可能包含该边的三角形数的比值[26],图2(b)中节点x和节点ω形成的连边exω的边聚类系数计算如式(11)所示:

边聚类系数准确地描述了一条边上三角模体的聚集程度。
定义1(模体密度(Motif Density,MD))对于网络中任意的待测节点x和y,ω是节点对的共邻节点,将路径wxωy的模体密度定义为包含路径wxωy的所有三角模体数目与所有可能包含该路径的三角模体数目的比值,如式(12)所示:

2.3 基于模体的朴素贝叶斯相似性指标
本文在对路径结构上模体密度进行分析和量化后,基于模体密度来分析路径的相似性贡献,进而在朴素贝叶斯指标的基础上提出改进的链路预测方法。
根据文献[17],LNB 方法将共邻节点ω的相似性贡献函数计算为待测节点x和y之间连接与不连接的概率之比,如式(13)所示:

其中:P(exy|ω)为ω的节点聚类系数,且满足P(exy|ω)+。Rω表示 共邻节点ω对待测节点产 生连边和不产生连边的贡献比。由于这种贡献函数的定义方式无法区分因路径模体特征不同而产生的贡献,为量化每条路径对节点相似性的影响,采用模体密度来定义路径的角色贡献函数。
定义2(基于路径模体密度的角色贡献函数)将路径wxωy的角色贡献函数R(wxωy)定义为在路径条件下,待测节点产生连边和不产生连边概率的比值,连边概率用模体密度来表示,如式(14)所示:

其中:P(exy|wxωy)表示路径wxωy对链接形成有促进作用,用该路径的模 体密度来计算;表示路径wxωy对链接形成有抑制作用。由式(14)可知,MMD(wxωy)越大,路径wxωy的促进作用越大,抑制作用越小,路径相似性贡献R(wxωy)就越大,与2.2 节的分析相符。因此,本文利用R(wxωy)量化路径wxωy对连边相似性的贡献是准确合理的。
定义3(基于模体的朴素贝叶斯链路预测指标)根据贝叶斯理论[17-19],在所有经过共邻节点路径的条件下,节点x和y连边与不连边概率的计算如式(15)和式(16)所示:

其中:W(x,y)表示经过共邻节点且连接节点x和y的所有路径的集合。
假设每条路径对待测连边的贡献是相互独立的,则:
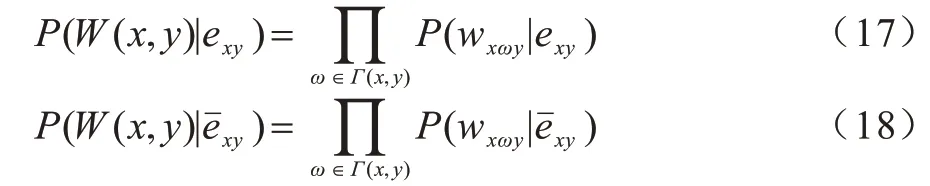
通过式(15)和式(16)相除的方式构建相似性指标,如式(19)所示:
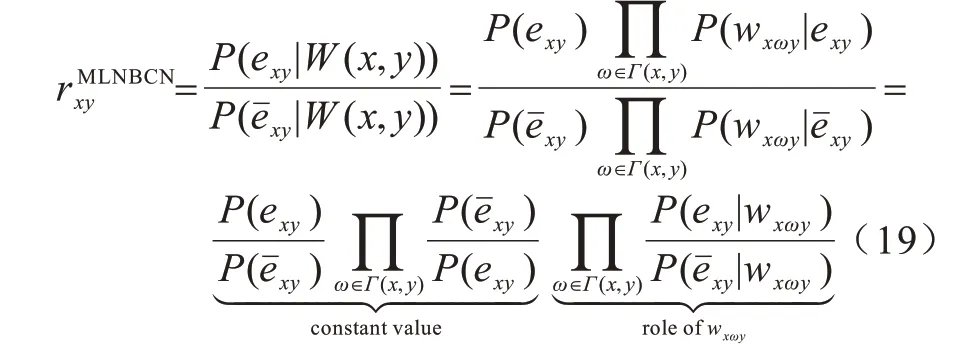
其中:P(exy)和P()分别表示整体网络中连边存在和不存在的概率,均为常数。P(exy)和P()的计算如式(20)和式(21)所示:

显然,s-1=也为常数,表示网络中连边存在和不存在的比值,可以忽略。
将式(14)、式(20)和式(21)代入式(19)中,等式两边取对数,得到其简化形式,如式(22)所示:

定义4(扩展指标)基于共邻节点的相似性预测模型有很多经典的预测指标。受LNB 模型启发,为进一步验证MLNB 方法的有效性,本文把MLNB思想应用到AA 指标和RA 指标上,得到MLNB 扩展指标,如式(23)和式(24)所示:

3 实验与结果分析
3.1 实验数据与预分析
为了评价MLNB 指标的预测准确性,本文在Football网络[27]、USAir网络[28]、C.elegans网络[29]、FWMW 网络[30]、FWEW 网络[31]和FWFW 网络[32]这6 个真实网络上进行实验。不同的网络具有不同的模体特征。当网络具有显著的模体特征时,挖掘模体特征的链路预测方法在性能上显著区别于传统的链路预测方法。因此,本文在进行仿真实验之前,首先要检验网络模体的存在性。本文基于2.1 节的模体基本理论以及Rand-ESU[33]算法,通过模体发现软件FANMOD 对6 个网络进行模体存在性检验。6 个网络的特征参数及模体存在性检验如表1 所示。从表1 可以看出,Z得分为正数,P值为0,说明以上6 种网络都有三角模体特征,可以用来测试MLNB 方法的准确度。

表1 6 个网络的特征参数与模体存在性检验Table 1 Feature parameters and motif existence test of six networks
3.2 评价指标
为了量化链路预测方法的准确性,一般将边集E随机划分为训练集ET和测试集EP,满足E=ET∪EP,并且ET∩EP=∅。训练集ET作为可观察到的已知网络信息用于计算待测节点对的相似性分数。测试集EP作为待预测的网络信息用于验证预测的准确性。本文使用AUC(Area Under the Curve)值[34]、精确度(P)[35]来评价链路预测方法。AUC 从整体上衡量方法的准确性,P衡量局部预测的准确性。
AUC 值可解释为随机选择一条缺失边(即EP中的边)的分数值大于随机选择一条不存在边(即U-E中的边)的分数值的概率。本文进行n次独立抽取,如果有n′次缺失边的分数值更高,n″次抽取两条边的分数值相等。AUC 值如式(25)所示:

精确度(P)计算前L条边的预测准确率。将预测边的相似性得分按照降序进行排序,如果在测试集中排名前L的有m条边,那么精确度计算如式(26)所示:

由于本文选取6 个真实网络的规模不同,因此统一将各数据集边数的10%作为L的值。
3.3 仿真实验结果分析
本文实验针对6 个具有模体特征的网络进行仿真实验,采用随机抽样方法按9∶1 划分训练集和测试集。为了消除随机误差的影响,对每个网络进行100 次独立实验并取平均值。本文将提出的MLNBs指标与局部属性的CN 指标、AA 指标、RA 指标、LNBs 指标,半局部属性的LP 指标和全局属性的Katz 指标进行对比。在多个不同类型网络中MLNBs 指标与现有指标的AUC 值对比如表2所示。

表2 不同指标的AUC 值对比Table 2 AUC values comparison among different indexs
从表2 可以看出,在每个网络上MLNBs 系列指标(MLNBCN、MLNBAA、MLNBRA)的AUC 值均优于对应的原始指标(CN、AA、RA)和LNBs 指标(LNBCN、LNBAA、LNBRA),表明路径模体密度对链路形成的可能性是有一定的影响。在MLNBs 系列指标中,MLNBRA 指标的AUC 值最高,MLNBAA指标次之,MLNBCN 指标最低,这说明惩罚度大的共邻节点能够有效提高预测精度。MLNBRA 指标的AUC 值在Football 网络中仅次于LP 和Katz 指标,相差不超过1%,在剩余的网络中MLNBRA 指标均具有较优的AUC 值。LP 指标在共同邻居的基础上考虑了三阶路径信息。Katz 指标考虑全局信息,时间复杂度相对较高。因此,LP 指标和Katz 指标的预测精度有一定优势。而MLNBs 系列指标计算二阶路径的局部信息,时间复杂度低于LP 和Katz 指标。本文提出的MLNB 方法能解释路径模体聚集程度与节点对链接的关系,且复杂度低于半局部和全局方法,在含有模体的网络上具有较优的适用性。
在FWMW、FWEW、FWFW 这3 个食物链网络中,MLNBs 系列指标的AUC 值均优于所有的基准指标。若以次优的全局Katz 指标为基准,MLNBs 系列指标的AUC 值在FWMW 网络中至少提升了5%,在FWEW 网络中至少提升了2%,在FWFW 网络中至少提升了7%。从表1 可以看出,FWMW、FWEW、FWFW 网络的三角模体平均频率较大,说明食物链网络中存在大量的三角模体,对于这类模体特征较为明显的网络,基于模体特征的MLNB 方法预测的效果更好,进一步验证了MLNB 指标针对此类网络具有一定的的有效性和可行性。
在不同类型网络中MLNBs 系列指标与现有指标的精确度对比如表3 所示,所有指标的预测结果在0~0.28,大多数指标的精确度小于0.2。
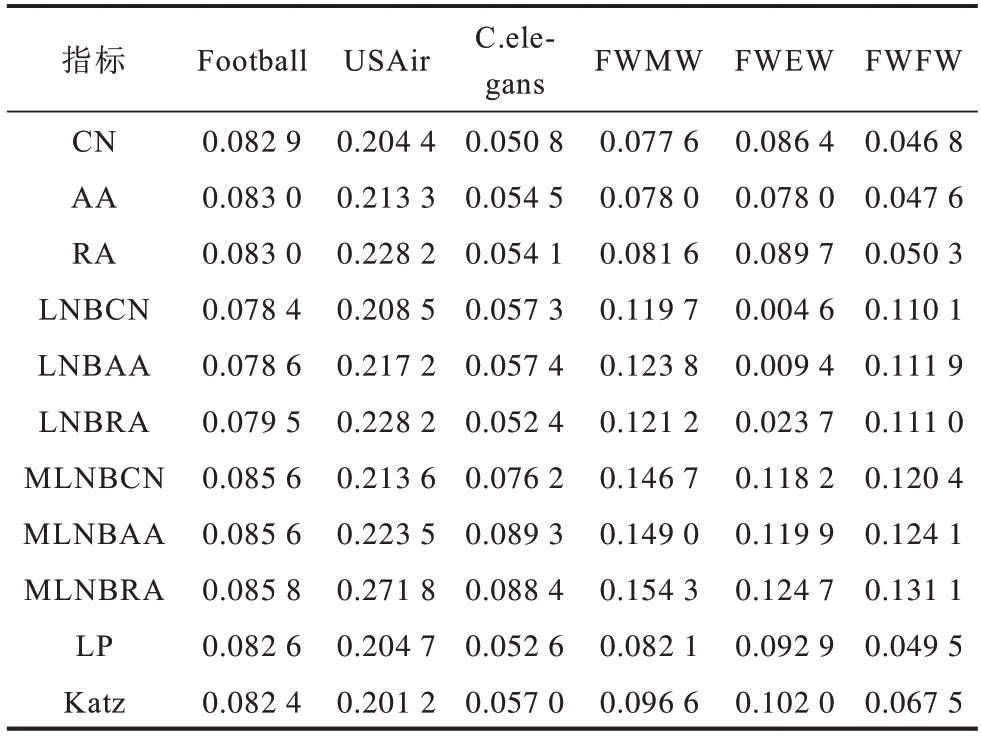
表3 不同指标的精确度对比Table 3 Precision comparison among different indexs
在USAir 网络中,MLNBs 系列指标(MLNBCN、MLNBAA、MLNBRA)的精确度不仅优于对应的原始指标(CN、AA、RA)和LNBs 系列指标(LNBCN、LNBAA、LNBRA),而且相对半局部LP 指标和全局Katz 指标也有明显提升。其中MLNBRA 指标的精确度最优,RA 和LNBRA 指标的精确度次优。精确度分析结果说明在USAir 网络中,共邻节点的度对链路的形成具有较大作用。在剩余的网络中,MLNBs 系列指标的精确度均优于所有的基准指标。在所有网络中,MLNBs 系列指标的精确度由大到小排序:MLNBRA>MLNBAA>MLNBCN。从表3 可以看出,基于模体特征的MLNB 指标的精确度相比局部和全局指标有较大幅度提升,证明了计算模体结构信息有助于提升预测性能。
3.4 鲁棒性分析
为了进一步分析MLNBs 指标的鲁棒性,本节在不同的训练集比例下研究MLNBs 指标与基准指标预测结果的变化情况。在不同网络中各指标的预测值仍然是取100 次独立实验的平均值。当训练集比例从0.6 开始每次增加0.1 直到0.9 时,各指标的AUC 值对比如图3 所示。

图3 在不同的训练集比例下各指标的AUC 值对比Fig.3 AUC values comparison among various indexs under different training set proportions
从图3 可以看出,当训练集比例增加时,多数指标的AUC 值随之增大,这是由于训练集比例增加使网络中共邻节点数目和已知拓扑信息增加,预测性能也随之提升。MLNBs 指标的AUC 值随训练集比例增大而增大。当可观测数据仅有60%时,除了USAir 和C.elegans 网络中MLNBs 指标相对局部相似性指标变化范围不大,在其余网络中仍取得相对较优的预测结果,表明MLNBs 指标在不同网络中具有较优的鲁棒性。LNBs 指标在FWMW、FWEW、FWFW 网络中并不遵从预测值随训练集比例增大而增大的规律,说明这3 个网络中LNBs 指标对训练集比例变化的敏感程度不同。
当训练集比例从0.6 开始每次增加0.1 直到0.9时,各指标的精确度对比如图4 所示。
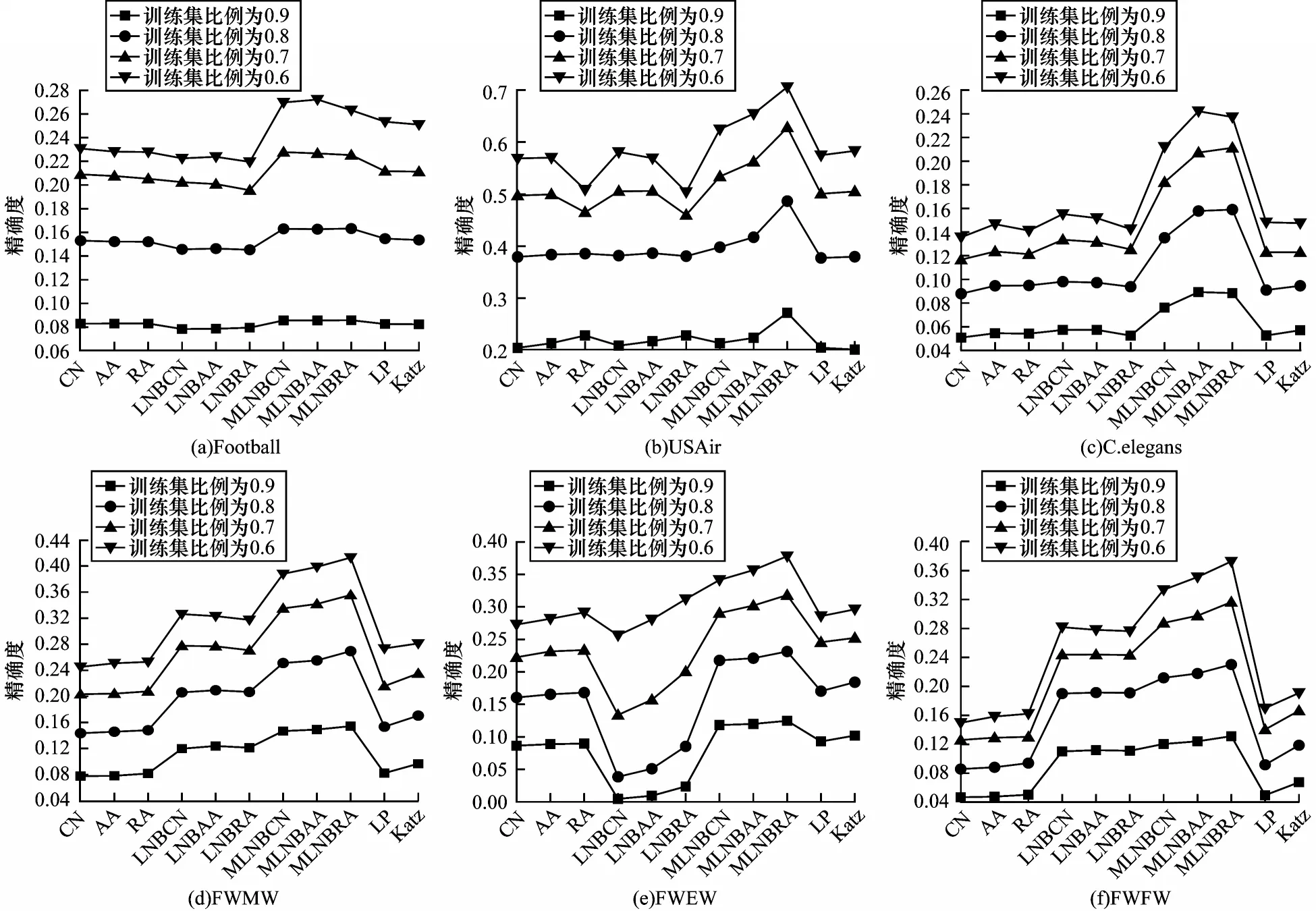
图4 在不同的训练集比例下各指标的精确度对比Fig.4 Precision comparison among various indexs under different training set proportions
与AUC 值的变化规律相反,图4 中各指标的精确度随训练集比例的增加而下降,这是由于精确度计算前L条边预测的准确率,训练集比例越大,前L条预测边在测试集中的可能性越小,精确度就越小。当可观测数据仅有60%时,在各网络中MLNBs指标(MLNBCN、MLNBAA、MLNBRA)的精确度均优于对应的原始指标(CN、AA、RA)和LNBs 指标(LNBCN、LNBAA、LNBRA),相对LP 和Katz 指标也有明显提升,这表明MLNBs 指标具有较优的鲁棒性。
无论训练集如何划分,在图3中Football和C.elegans网络上的LP、Katz 指标相较于MLNBs 指标的AUC 值有一定的优势,而图4 中LP、Katz 指标的精确度都低于MLNBs 指标,说明LP 和Katz 指标并不是在所有评价指标下都表现良好。因此,MLNBs 指标在AUC 值和精确度两种评价指标测试下具有较优的性能,与不同基准指标相比,在各网络中具有较优的鲁棒性。
4 结束语
本文针对具有模体特征的网络提出一种基于模体的朴素贝叶斯链路预测方法。从模体角度定义模体密度来描述路径结构上模体的聚集程度。考虑到路径结构上模体密度对链接形成的作用,构建基于路径的角色贡献函数,以量化路径的相似性贡献。在此基础上,结合朴素贝叶斯理论,推导MLNBCN及其扩展指标。实验结果表明,本文方法具有较优的鲁棒性,所提相似性指标的AUC 值和精确度均优于LNBs 指标和CN、AA、RA 等基准指标。本文所提的链路预测方法仅针对无权无向、含有模体结构的网络,后续将本文方法MLNB 应用到加权有向网络中,研究加权有向网络的模体特征对链路预测准确度的影响。此外,设计适用于更多不同领域网络的链路预测方法也是下一步的重点研究方向。

