倒Y 型四能级系统中吸收谱线的窄化极限研究*

邸凤清 贾宁 钱静‡

1) (华东师范大学物理与电子科学学院,上海 200241)

2) (上海理工大学公共实验中心,上海 200093)

基于倒Y 型四能级系统,理论研究了探测光吸收谱线的线宽窄化极限.发现得益于中间激发态与另一超精细基态之间施加的第三束控制光,线宽窄化极限的限制条件转变为两个基态能级之间的相干衰减率,而非基态与高激发态之间.与传统的梯型结构相比,吸收光谱线宽的窄化极限能够提高2 个数量级.研究表明,通过适当调节这束控制光的拉比频率和失谐量,可以获得兼具超窄线宽和高对比度的吸收光谱信号.数值计算结果与理论分析完全相符.此外,还讨论了吸收谱线对光场的响应规律和多普勒效应的影响.对原子热运动的研究发现,倒Y 模型由于缺少三光子作用的过程而无法完全消除多普勒增宽的影响.借助传播光场的优化设计可以减小多普勒效应的影响,在有限温度下获得较窄的吸收谱线.本文的研究成果对高分辨光谱学的实验发展具有重要的指导意义.

1 引言

光谱的自然线宽通常取决于能级的寿命.根据测不准原理,在任意时刻原子所处的能级都有一定的宽度,从而导致谱线加宽,即谱线的自然加宽.存在多种机制会使谱线宽度大于自然线宽,如气体分子间的碰撞以及气体与容器壁间的碰撞会导致碰撞加宽[1],由于气体分子的多普勒效应引起多普勒加宽[2]等.自然(甚至亚自然)线宽在高分辨率光谱[3,4]、精密光谱测量[5]、高精密的激光稳频和锁相[6]、慢光光学[7]等领域有着重要的应用价值.因此,发展对谱线极限线宽机制的物理研究非常重要.在三能级原子系统中,早期实现的亚自然线宽与相干布居俘获现象有关[8],之后Gauthier 等[9]发现通过改变光场的拉比频率可以将线宽压缩到自然线宽以下.在多普勒增宽介质中,通过增加三能级系统中强耦合光场的失谐,利用原子相干和干涉效应,可以得到亚多普勒线宽[10,11].此外,Iftiquar 和Natarajan[12]在 Λ 型三能级系统中利用能级的塞曼分裂令EIT (electromagnetic induced transparency)窗口发生劈裂从而实现谱线的窄化.除了三能级系统以外,人们也对两泵浦场驱动下的各种四能级系统进行了研究,观察到亚多普勒和亚自然线宽现象[13-15].

倒Y 型四能级系统兼具梯型和 Λ 型两种三能级结构的特点,一直受到科学家们的关注[16,17].相对于梯型系统,倒Y 结构中额外的第三束光场耦合基态与中间激发态充当控制端的角色,可以有效地调节探测光的吸收特性,优化体系的信号输出.类似地,正Y 型系统通过两个激发通道之间的量子干涉也能影响探测光的吸收[18,19].Qi[20]研究了倒Y 型系统中探测光的单和双EIT 窗口与两束耦合光的幅值以及失谐之间的关系,发现通过调节耦合光的幅值和失谐可以获得亚自然线宽的吸收谱线,但并没有对窄化谱线出现的位置和宽度进行定量研究.Ghosh 等[21]发现在倒Y 型系统中,利用多普勒效应可以使探测光EIT 信号的线宽大大窄化,得到几十kHz 宽度的超窄谱线.上述关于利用多普勒效应实现谱线窄化的研究,大多数关注如何窄化EIT的透射窗口,很少有工作对探测光吸收光谱的线宽窄化进行研究.窄线宽的吸收光谱同样具有重要的应用价值,如可以被用在高灵敏度的微波探测[22]和提高光学微谐振器的性能[23]等方面.

本文详细研究了倒Y 型四能级系统中探测光吸收光谱线宽的窄化极限问题,提出通过适当地调节第三束控制光的拉比频率和能级失谐能够有效窄化谱线的线宽.考虑到在强耦合光作用下,梯型三能级系统的中间能级和上能级形成缀饰态,吸收谱线的线宽极限取决于激发态与基态能级之间的相干衰减率.通常情况下,能级的相干衰减率与其寿命反相关,高激发态对应的能级寿命短故相干衰减率比较大,可以达百kHz 甚至MHz的量级.本文提出利用倒Y 系统的优势,在中间激发态与另一超精细基态能级之间施加第三束控制光.通过调节这束光的失谐和拉比频率可以使吸收谱线的线宽极限仅受限于两个基态之间的相干衰减率,而非基态与激发态之间.这大大减小了线宽窄化的极限值,通常仅为数kHz的量级.讨论了吸收谱线对控制光的时间响应,发现在获得窄线宽的同时不可避免地会延长系统到达稳态的时间.此外还定量研究了吸收谱线的窄化率和对比度与附加光场之间的依赖关系,以及加入控制光前后吸收谱线的变化.与三能级梯型结构比较的结果表明,倒Y 型原子模型的吸收光谱信号兼具超窄线宽和高对比度的优点.研究结果为多能级系统中非线性光学效应的研究提供了更多思路[24-26],也进一步指引了高分辨光谱学的发展方向[27-29].

2 理论解释

如图1(a)所示,倒Y 型四能级原子系统包含基态|g〉,中间态|e〉和激发态|r〉,构成传统的梯型结构,探测光Ωp和耦合光Ωc分别驱动|g〉↔|e〉和|e〉↔|r〉之间的能级跃迁;另外,第三束光Ωd耦合|e〉和另一基态超精细能级|m〉,充当控制光的角色,可以影响探测光的吸收和原子自身的激发.δ,δc和Δ分别表示探测光、耦合光和控制光的单光子失谐量.与梯型系统相比,附加的第三束光Ωd可对系统谱线线宽起到进一步的调节作用,因此倒Y 型系统具有更大的灵活性[30].实验上,可通过扫描δ研究探测光的吸收光谱特征.考虑到体系可能存在的各种耗散机制,这里我定义Γα表征能级|α〉的总自发辐射衰减率,γαβ表征任意两能级|α〉和|β〉之间的相干衰减率.

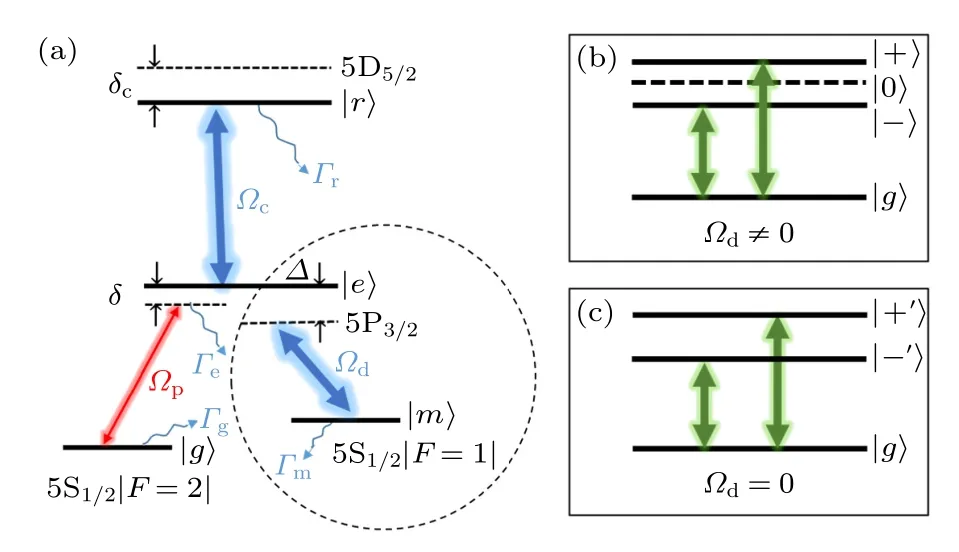
图1 (a) 倒Y 型四能级原子系统的裸态能级示意图;(b)考虑 Ωd/=0 时,在满足 Δ+δc=0的情况下缀饰态能级|±〉与基态 |g〉 发生耦合,而能级 |0〉 由于不包含裸态 |e〉,故不与 |g〉 耦合;(c) 反映了不存在控制光 Ωd的情况下,系统约化为三能级梯型结构所对应的缀饰态能级 |±′〉 与基态|g〉之间的耦合Fig.1.(a) Schematic of an inverted-Y type four-level atomic system coupling with three light fields Ωp,Ωc,Ωd ;(b)for Ωd/=0 and Δ+δc=0,the ground state |g〉 only couples with |±〉 (dressed states);(c) While Ωd=0,the system reduces to a three-level ladder structure where|g〉couples with the other two dressed states |±′〉 .

在旋转波近似下,用于描述光与原子系统相互作用的哈密顿量可以写成(ℏ=1):

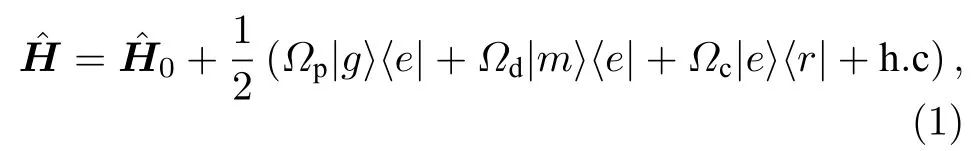
这里,=−(δ|e〉〈e|+(δ −Δ)|m〉〈m|+(δ+δc)|r〉〈r|)表示单原子的哈密顿量.δ −Δ和δ+δc分别表示 Λ型(|g〉,|e〉,|m〉) 和梯型 (|g〉,|e〉,|r〉) 结构中的双光子失谐.与级联型四能级结构不同,该系统不包含三光子过程.

2.1 本征态分析

当δc/=−Δ时,倒Y 型系统可存在两个EIT窗口,对应三个吸收峰[20].吸收峰的位置和宽度均受到光场强度 (Ωc,Ωd) 及失谐量 (δc,Δ)的影响.而当条件

满足时,系统在缀饰态表象下可被看作三能级系统,本征值和本征态都大大简化.为了与梯型三能级系统进行定量类比,并清晰地体现控制光Ωd的调节作用,首先假设δc=−Δ成立.在3.2 节中会在δc/=−Δ的情况下,详细地讨论结果的普适性.

考虑到弱探测近似Ωp≪Ωc,Ωd,对角化哈密顿量可求得本征值的解析表达式:

这里t anθ=其中等效拉比频率为表示所有原子始终处于基态未激发.从(4b)式—(4d)式可以看出,缀饰态|0〉仅包含|m〉和|r〉,故与|D〉不发生直接耦合,对探测光场表现为不吸收.只有缀饰态|−〉和|+〉中包含组分|e〉,可与|D〉在和处发生耦合,使原子有一定概率激发到除|g〉以外的其他原子能级上,对探测光表现为吸收[31].如图1(b)所示,由于|g〉只与|+〉和|−〉耦合,系统此时可看作包含|g〉,|+〉和|−〉三个能级,吸收谱线表现为双峰结构.当Δ=0 时,双吸收峰是关于探测共振频率δ=0 对称的,该现象被称为Aulter-Townes(AT)分裂,而双峰间距恰好等于Ω[32].与三能级系统一样,在倒Y 型系统中,当控制光的单光子失谐Δ不等于0 时,这种对称结构被破坏.

在强耦合场Ωc的情况下,探测光吸收曲线由EIT 过渡到AT 双峰[33,34].本文主要研究吸收峰的窄化与附加控制光场Ωd的关系,并利用缀饰理论解释其谱线窄化的物理机理.通常情况下,探测光吸收谱线的最小宽度受限于能级之间的相干衰减率,而激发态|r〉与基态|g〉间的相干衰减率γrg与能级自发衰减率Γr和Γg有关,表示为γrg=(Γr+Γg)/2,高达百kHz的数量级[16].如激发态|5D5/2〉的能级寿命约为238.5 ns[35],相应的能级自发辐射衰减率达 680 kHz[16].在传统的梯型EIT 过程中,由于|g〉与|e〉和|r〉之间存在相干性,谱线线宽受γeg和γrg共同影响,因此通过减小上能级与基态之间的γrg,可以实现谱线的窄化[36],如选择能级寿命较长的高激发里德伯态.而我们的研究进一步揭示出,在倒Y 型结构中通过调节控制光Ωd可以改变原子介质对探测光的吸收,建立两个基态超精细能级|g〉和|m〉之间的直接关联.从而令吸收谱线窄化的极限仅取决于|g〉和|m〉之间的相干衰减率γmg,而非激发态与基态之间的γrg或者γeg.通常情况下,满足γmg≪γrg,γeg的条件将有望获得超窄的吸收谱线.

2.2 谱线线宽的定义

谱线的自然线宽取决于原子能级的寿命.以简单的二能级原子为例阐述谱线线宽的估算.在二能级原子模型中,若上、下能级的自发辐射寿命分别为τ1和τ2,根据海森伯不确定原理,每个能级的能量Ei都具有一定的分布宽度 ΔEi,满足ΔEi·τi ≈ℏ(i=1,2),即 ΔEi ≈ℏΓi.这里Γ1,2代表能级的自发衰减率,约为能级寿命的倒数.因此能量总的不确定量可写成 ΔE=ℏ·Δω ≈ℏ(Γ1+Γ2),进而谱线的宽度为Δω ≈Γ1+Γ2=2γ12[37].这里γ12是上下能级之间的相干衰减率.对于更复杂的能级系统,谱线的宽度将受多个能级间的相干衰减率和耦合相互作用的共同影响.

在倒Y 型系统中,定量研究如何有效调节Ωd实现谱线线宽窄化及极限宽度的计算,揭示AT 分裂现象的物理本质.在缀饰表象下,|D〉与|+〉(|−〉)分别在δ+(δ−)处发生跃迁,能级跃迁形成的两个探测吸收峰分别对应于缀饰态能级|±〉与|D〉之间的共振吸收,吸收峰的宽度与|+〉(|−〉)和基态间的相干衰减率γ+D(γ−D)有关,满足w±D=2γ±D.根据(4c)式和(4d)式,γ±D应由能级|m〉,|e〉,|r〉与基态|g〉之间的相干衰减率γmg,γeg和γrg共同决定[38].因此,可以写出δ+(δ−)两处吸收光谱的等效线宽w+D(w−D),表示为

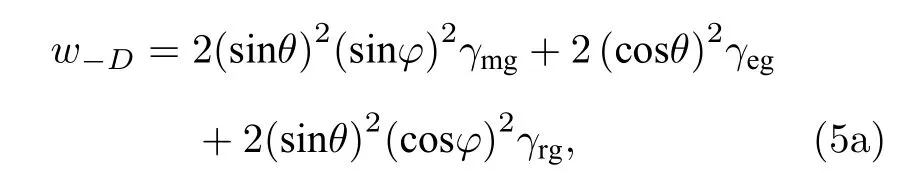
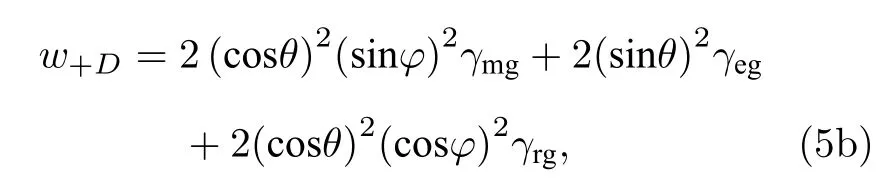
本质上与|m〉,|e〉,|r〉裸态上的布居数和能级的自发衰减率有关.当Δ=0 时发生单光子共振耦合,sinθ=cosθ,此时w+D=w−D表示两个吸收峰的谱线宽度相等;当Δ/=0 时,sinθ/=cosθ,两个吸收峰的谱线宽度不等.考虑到Δ ＞0 和Δ ＜0的结果类似,本文仅研究Δ ＞0的情况.

随着Δ的增大 sinθ趋于 0,cosθ趋于 1,由于γmg≪γrg≪γeg,因此位置处的w−D逐渐增大位置处的w+D逐渐减小.本文重点研究w+D的窄化,将θ,φ的表达式代入(5b)式中,得到:

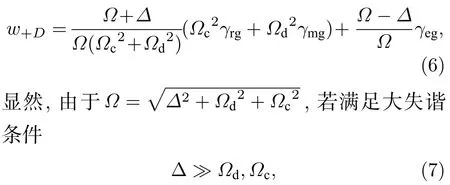
在讨论线宽的同时,实际应用中EIT 吸收或者透射峰的对比度也十分重要,一般认为对比度越高,线宽越窄对研究越有帮助[39].因此,用

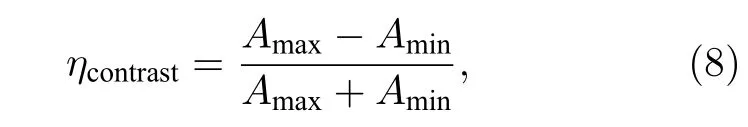
来表征谱线的对比度,其中Amax和Amin分别表示吸收峰的最大和最小值.

2.3 线宽极限的数值验证

数值验证中,选用合适的87Rb 原子能级,详见4.3 节.Γα(β)表示能级|α(β)〉(α,β ∈(g,m,e,r))的总自发衰减速率,则两能级之间的相干衰减率满足本文先以Γe作为频率单位估算其他参数,分别为γmg=γgm=1.667×10−4(约1 kHz),γeg=0.5(约3.0 MHz),γrg=0.057(约340 kHz),γre=0.557(约3.34 MHz) .

考虑存在各种耗散机制,采取主方程的方法进行数值计算.密度矩阵主方程的普适形式为

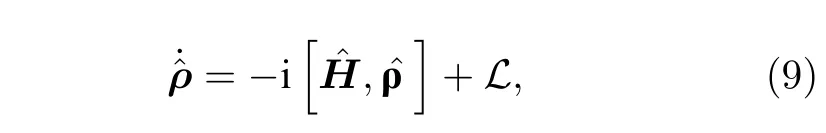
其中是 4×4的密度矩阵算符,的表达式见(1)式,L为Lindblad 算符,表征了体系的耗散过程,可写为[40]

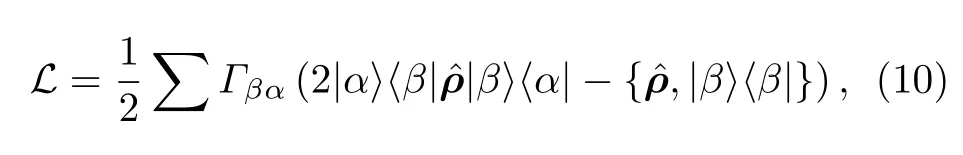
这里,{βα}∈{eg,em,re,mg,gm},Γαβ为能级|α〉到|β〉的自发衰减速率.由于相干衰减率且能级的总自发衰减率Γr=Γre,Γg=Γgm,Γm=Γmg,Γe=Γeg+Γem,故将和L的表达式代入主方程(9),整理之后可得描述原子与多光场相互作用的光学Bloch 方程.这里,非对角项ραβ的随时演化满足

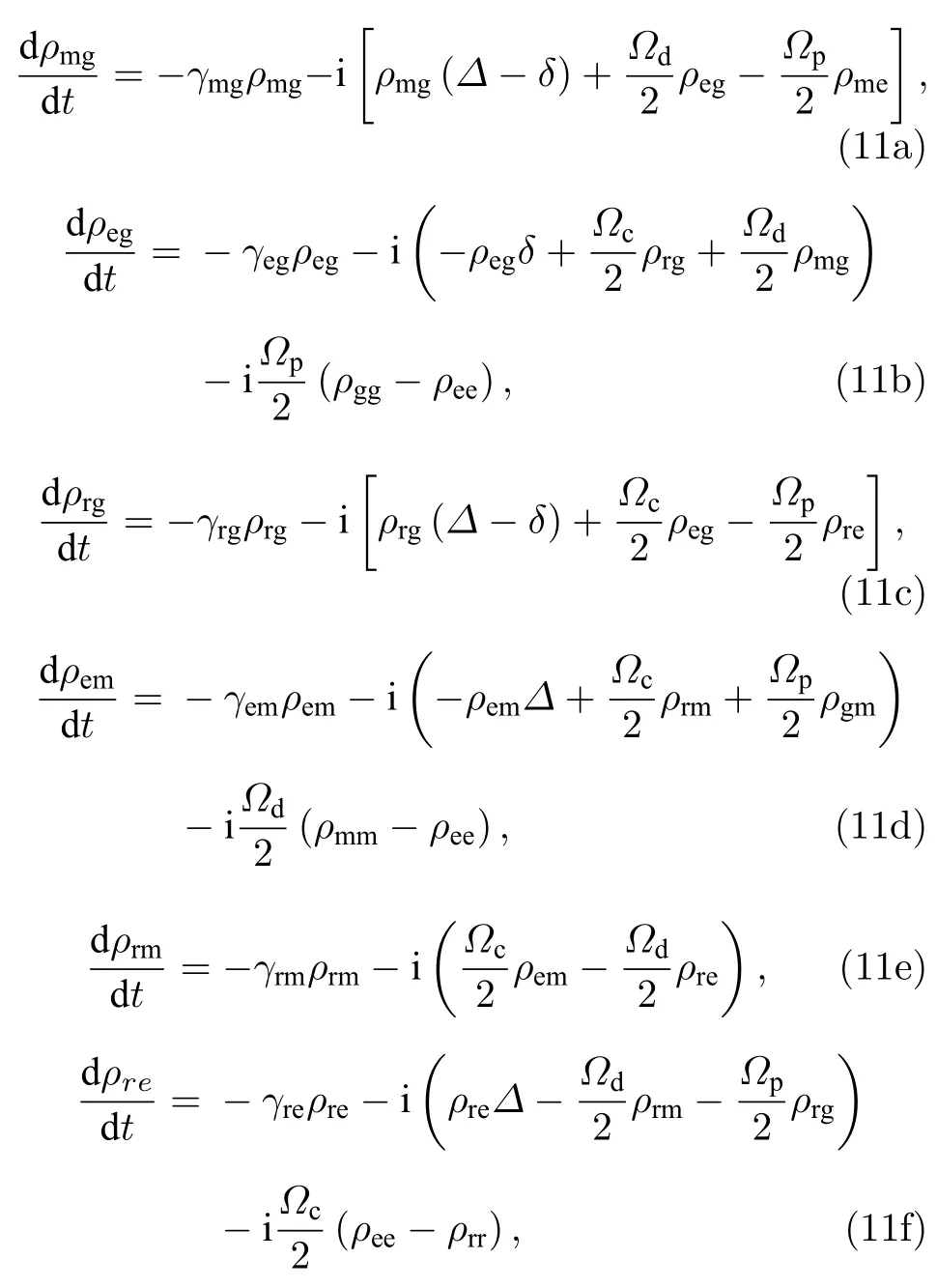
而对角项ραα的时间演化满足

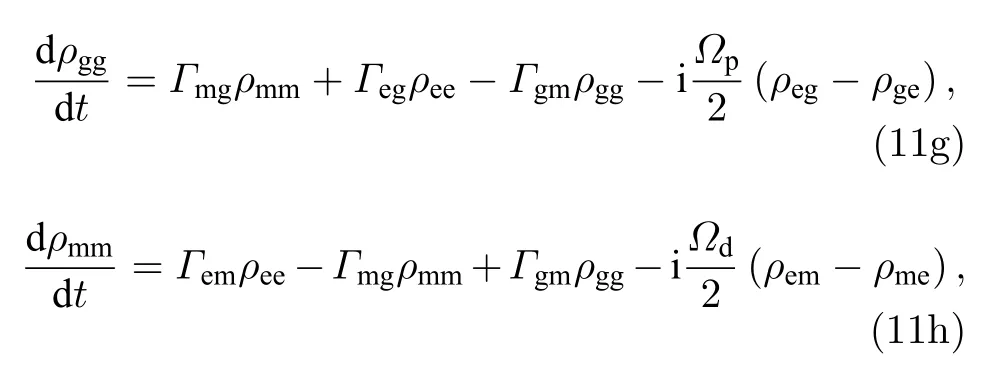
根据理论公式(6)可知,在满足Δ ≫Ωc,Ωd且Ωd→0 时(等同于梯型结构),线宽w+D趋近于2γrg(约 680 kHz).然而,凭借辅助光场Ωd的有效调节,有望获得倒Y 系统谱线窄化的极限值为

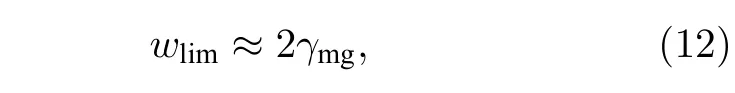
毫无疑问,能级间的相干衰减率γmg较γrg小两个数量级,可以实现对谱线线宽的极大窄化.从图2(a)可以很明显地看出,两条曲线在Ωd较小的时候并不符合,原因是此处弱探测场假设Ωd≫Ωp失效,导致理论估算值(红色虚线)与数值计算结果(蓝色实线)差异较大.然而,当Ωd增大时,两者趋向于一致,也验证了本文理论的正确性.另外也发现,根据理论分析可以得出,有效调节辅助光场Ωd可获得窄化线宽的极限值wlim((12)式);但理论估算的结果为伴随着Ωd增大,谱线线宽w+D逐渐减小直至最小值,约为23 kHz,随后不断增加.其原因主要是 Δ≫Ωc,Ωd的条件限制了Ωd的可调节范围,这点将在3.1 节详细讨论.数值结果给出的线宽表明,只有当Ωd足够小时,才能获得极窄的谱线.然而研究发现,当Ωd趋近于0 时虽然谱线线宽不断趋向于wlim,但也伴随着信号对比度ηcontrast的急剧下降,如图2(b)所描绘,因此在实验上很难观测到该信号.实验中往往希望兼顾窄线宽和高对比度两方面的优势,所以通过调节附加光场Ωd发现,当Ωd/Γe=1.1 时,w+D=23 kHz,ηcontrast=0.99,如图2(b)中箭头所指位置.实验上,在谱线对比度可接受的范围内应尽量减小控制光的拉比频率Ωd,此时得益于超精细基态能级之间的相干衰减率γmg的主导作用,不仅可以得到比传统的光学跃迁过程小很多的线宽,同时谱线还具有很高的对比度,在量子信息存储以及高分辨光谱等领域具有重要的应用价值[42-46].

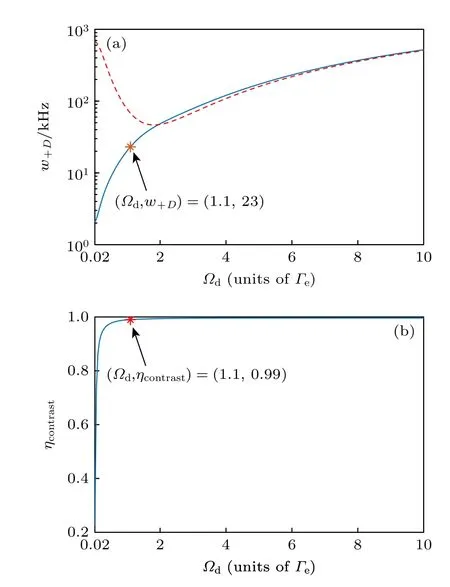
图2 (a) δ=δ+ 处吸收谱线的线宽 w+D 与 Ωd的关系.红色虚线是根据(6)式得到的理论结果,蓝色实线是数值计算的结果.(b) δ=δ+ 处吸收谱线的对比度 ηcontrast 与Ωd的依赖关系.计算所取参数为Ωp=0.03,Ωc=0.3,Δ=15,δc=−15.箭头所指位置表示对比度 ηcontrast 达到0.99 对应的Ωd 和 w+D的取值Fig.2.(a) Absorption linewidth w+D vs the coupling-field Rabi frequency Ωd .Theoretical (Eq.(6)) and numerical results are plotted by red-dashed and blue-solid curves,respectively.(b) Spectrum contrast ηcontrast vs Ωd for δ=δ+ .Arrow shows the location of (Ωd,w+D,ηcontrast)=(1.1Γe,23 KHz,0.99).Simulation parameters are Ωp=0.03 ,Ωc=0.3,Δ=15 and δc=−15 .

2.4 与三能级梯型系统的比较

进一步研究三能级梯型结构的谱线窄化问题,考虑该体系仅包含能级|g〉,|e〉,|r〉.如图1(c)所示,在处存在两个吸收峰,其中δ+′=处的光谱线宽可表为

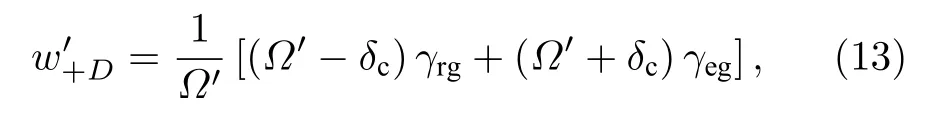
图3 三能级梯型系统中,在 δ=位置处吸收谱线线宽=与0.3控制光失谐量 |δc|的依赖关系.这里取 Ωp=0.03,Fig.3.In a three-level Ladder system the spectrum linewidth w vs detuning |δc| .Here Ωp=0.03 ,Ωc=0.3 .

3 能级失谐的影响

为了进一步探究吸收谱线的窄化线宽极限与其他参量的依赖关系,本节考虑各因素的影响.

3.1 失谐量的大小

2.1 节中为了推导吸收谱线窄化极限线宽的解析表达,假设条件δc=−Δ成立,此时倒Y 模型可视作约化的三能级(如图1(b))进行研究.下面进一步研究Δ的绝对大小对谱线窄化的影响.

当满足(7)式的条件即Δ ≫Ωc,Ωd时,(6)式可化简为

此时,若Ωc和Ωd的相对大小发生变化,导致线宽的可调范围变为w+D ∈2[γmg,γrg] .由于条件Δ ≫Ωd,Ωc无法严格满足,所以实际计算结果与预估范围略有区别.图4(a)和图4(b)给出了Ωd=0.5 和1.1两种情况下线宽和对比度随Δ的变化趋势.很明显,随着Δ的增大,谱线宽度w+D急剧减小并不断接近极限值 2γmg.当Δ=150 时(图上未显示,对应Δ=900 MHz),w+D可达 2.2 kHz,这与理论预估的极限值已非常接近.从图4(a)和图4(b)还可以看出,失谐量Δ的变化对谱线的对比度没有明显影响,如当Ωd=1.1 时,对比度可以保持在 0.99 附近.所以,在实际应用中通过增大Δ获得高质量谱线的方法还是十分可行的.

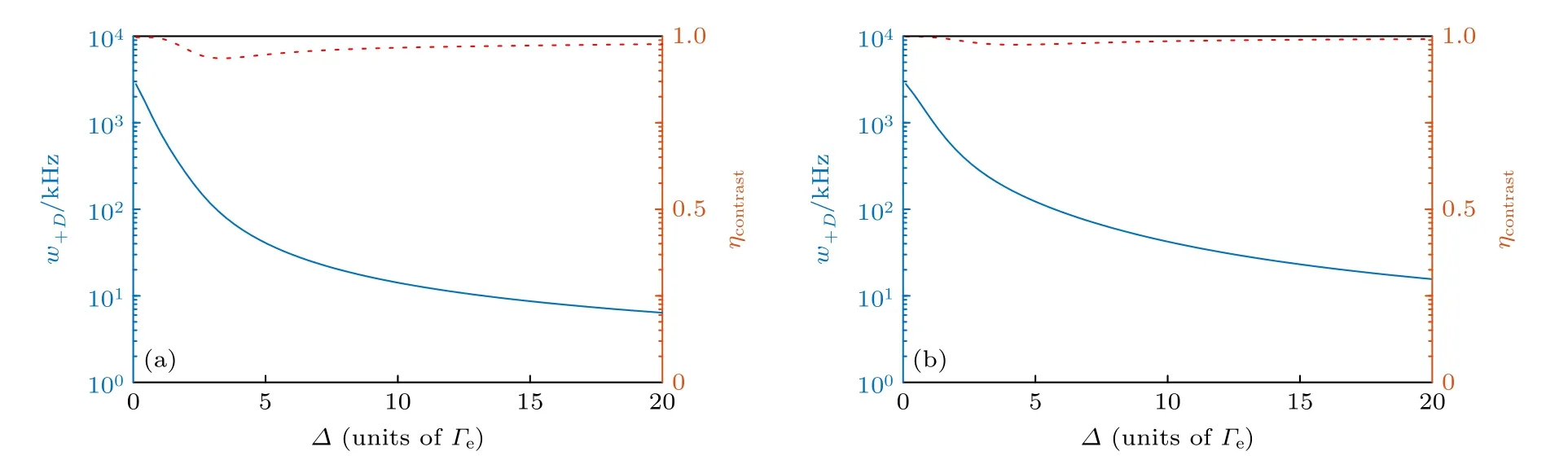
图4 (a)Ωd=0.5 和 (b)Ωd=1.1 两种情况下,δ=δ+ 处吸收谱线宽度 w+D (蓝色实线)和对比度 ηcontrast (红色虚线)随失谐量Δ的变化关系.其他参数和图2 相同Fig.4.Dependence of spectrum linewidth w+D (blue-solid) and contrast ηcontrast (red-dashed) on the detuning Δ under (a)Ωd=0.5and (b) Ωd=1.1 .Other parameters are same as in Fig.2.

为了便于直观比较,图4 中仅绘制了Δ ∈[0,20]的结果.当Δ=15 时,若Ωd=1.1 对应线宽w+D ≈23 kHz,对比度ηcontrast≈0.99 .为了使谱线宽度w+D进一步降低,可继续调节附加光场Ωd的大小.在Ωd=0.5 情况下,可以看出线宽w+D ≈9 kHz,对比度ηcontrast≈0.97 .相比于Ωd=1.1的情况,更小的Ωd可以得到更窄的线宽,但对比度也稍有降低,不利于实验上观察明显的吸收谱线.为了保证较好的对比度,选取最佳的Ωd=1.1,与图2 结果完全一致.实验上需要综合考虑线宽和对比度的实际需求,合理地选择附加光场的强度.

3.2 δc=−Δ 不满足时

为了体现研究结果的普适性,假设条件δc=−Δ不满足.此时吸收谱线一共存在三个吸收峰,分别位于Ω)≈0和δ ≈−δc处.倒Y 型系统可以看作梯型和Λ型三能级的组合.

这里依旧研究δ=δ+处吸收峰的窄化现象.注意到,若δ=Δ致使由|g〉,|e〉,|m〉组成的Λ 型三能级始终满足双光子共振条件,该共振引起的吸收谱线与上能级|r〉无关.故δc的改变不会影响δ=δ+≈Δ处的谱线线宽和对比度.数值验证可见图5(a)—图5(d),可以很直观地发现,在不同δc取值的情况下,δ=δ+处的吸收谱线外形几乎不变,与理论分析完全符合.这表明本文提出的倒Y 型四能级结构的理论解释拥有足够的普适性,线宽极限和对比度的分析结论均不依赖于参数δc的选择.

图5 (a)—(d)不同的δc 取值下,δ=δ+ 位置附近的吸收谱线.这里取 Ωd=1.1,Δ=15,其他参数和图2 相同Fig.5.(a)—(d) Absorption spectrum around δ=δ+ for δc=(−2Δ,−Δ,0,Δ) .Here we choose Ωd=1.1 and Δ=15 .Other parameters have been described in Fig.2.

4 实验可行性讨论

4.1 时间依赖的控制光场

在缀饰表象下的讨论中(见第2 节),我们发现如果采用大失谐的光场((7)式),并且控制光和耦合光的拉比频率满足Ωd≫Ωc时,激发态|+〉和基态|D〉的相干衰减率γ+D仅由|m〉和|g〉之间的相干衰减率γmg决定.由于γmg≪γrg≪γeg,可以在δ=δ+处获得非常窄的吸收谱线,宽度趋向于w+D→2γmg.然而,非常小的相干衰减率γ+D会延长系统到达稳态的时间.在实际实验过程中,开合激光的同时体系需要一定的响应时间才能恢复到一个新的稳态,因此有必要研究吸收谱线对光场的响应规律.

当没有加入控制光时(Ωd(t)=0),系统可看作三能级阶梯型结构,在大失谐的情况下,吸收峰峰值的高度非常低(约10−5) .当开启控制光后,系统将经过一定的响应时间后达到一个新的稳态(约10−2) .数值模拟了δ=δ+处吸收谱线的峰值随时间的变化,如图6(b)所示.当t=200 μs 时,开启控制光(Ωd(t)=6.6 MHz)导致吸收峰经过大约515 μs的响应时间之后达到新的稳态.这里,影响响应时间的主要因素是非常小的相干衰减率γ+D.为了更直观地展示吸收谱线的变化,图6(a1)—图6(a3)分别给出了 (t1,t2,t3)=(100,250,800)μs时δ=δ+处的吸收谱线.比较图6(a3)和图6(a1)可知,通过施加控制光可以有效地改善吸收谱线的特征,获得兼具窄线宽和高对比度的谱线.

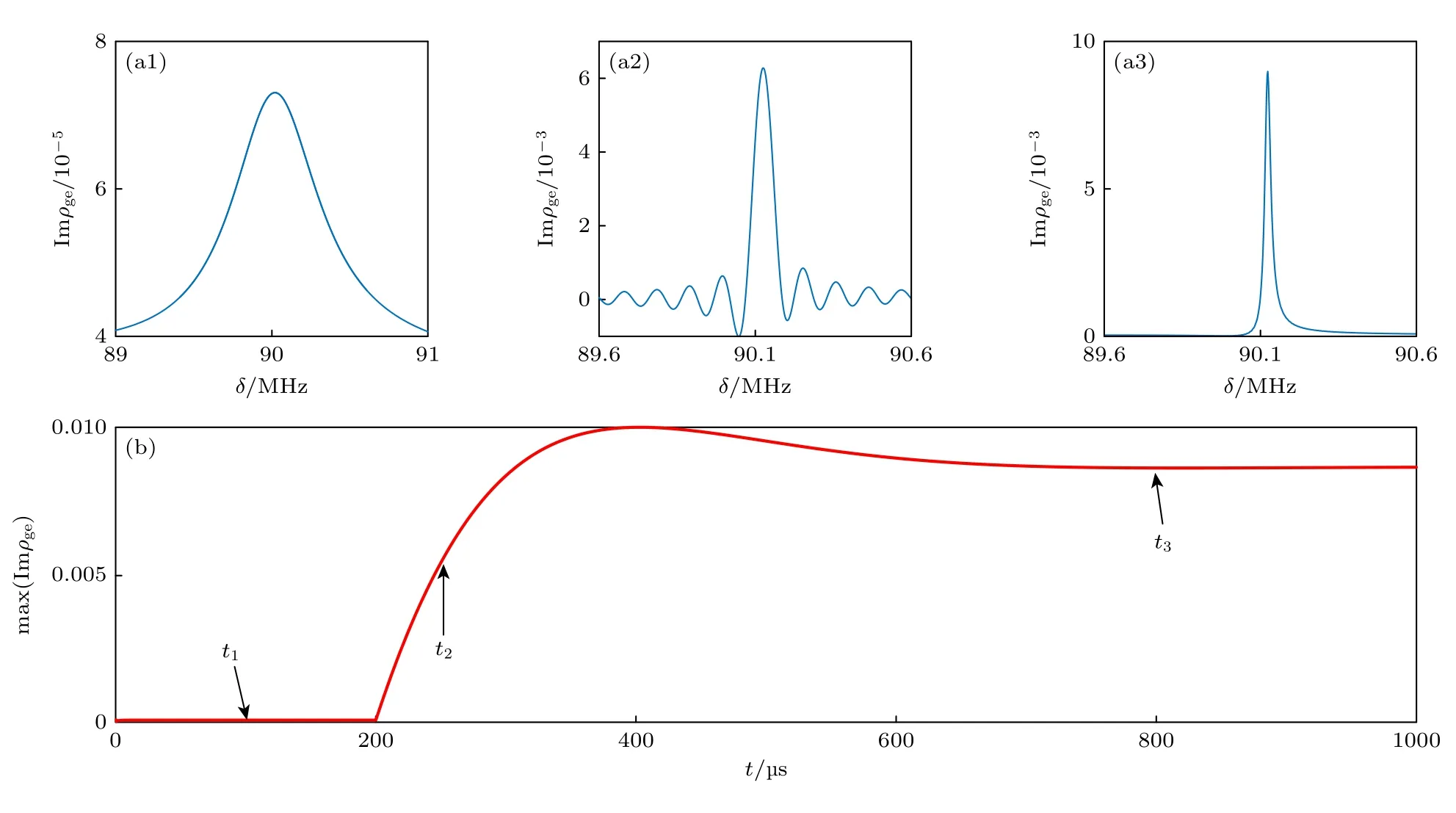
图6 考虑控制光场 Ωd(t) 在 t=200 μs 时开启,(a1)—(a3)当 t=(t1,t2,t3)=(100,250,800)μs 时 δ=δ+ 位置处的吸收谱线;(b) 该处吸 收谱线的峰值高度M ax(Imρge) 随时间 t的变化.当 t ＜200 μs 时,Ωd(t)=0 ;当 t ≥200 μs 时,Ωd(t)=6.6 MHzFig.6.In the case of a time-dependent control field which is Ωd(t)=0 for t ＜200 μs and Ωd(t)=6.6 MHz for t ≥200 μs .(a1)—(a3) The absorption spectrum at δ=δ+ ≈90.12 MHz when t=(t1,t2,t3)=(100,250,800)μs, respectively.(b) Time-dependent peak absorption Max(Imρge(t)) as a function of time t. The control field is turned on at t=200 μs .

4.2 原子热运动对谱线窄化的影响

在一定的温度T下,以速度v运动的原子将感受到多普勒频移,导致三束光场对应的单光子失谐量发生改变:kdv.这里令|kp,c,d|=2π/λ代表对应光场的波矢,λ=780 nm.此时,表征谱线吸收率的表达式可改写为[49]

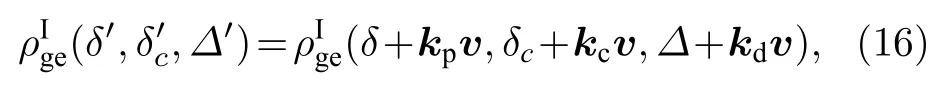
由麦克斯韦速率分布函数对原探测场的吸收率进行积分可得到新的谱线[50,51]:

代表速率函数,用来描述原子的运动分布,k,m,T分别表示玻尔兹曼常数、原子质量和原子温度.

为了减小多普勒效应的影响,假定原子速度v对双光子失谐量δ −Δ和δ+δc产生的修正可以忽略,即需要优化设计三束光场的传播方向:kp=kd(探测光与控制光同向传播),kp=−kc(探测光与耦合光反向传播)[52].该条件能够最大限度地补偿由于多普勒效应导致的谱线增宽,保证δ+位置处谱线的宽度最窄.数值结果如图7 所描绘,在不同的温度T下展现了谱线线宽和对比度与控制光强度的关系.与前人结果类似[29],谱线线宽随着温度的增加会明显增大,同时对比度也略有降低.也就是说,原子的热运动对谱线窄化是不利的因素.在温度较低(T ＜10−3K)时,我们理论预言的窄化线宽极限还是能够达到的.注意到,在倒Y 型四能级系统中不能完全消除多普勒效应的影响从而获得无多普勒增宽光谱,其根本原因是该模型只包含单光子和双光子激发过程,无法通过多光束传播方向的空间设计使得总波矢为0,进而不满足无多普勒增宽效应中波矢的空间匹配条件[53].这也是本文的模型有待下一步完善的地方.

图7 不同的温度 T=(10-2,10-3,0)K 下,(a) w+D 和(b) ηcontrast 与 Ωd的依赖关系.选取的参数是 Δ=90 MHz,δc=−Δ,其他和图2 相同Fig.7.Under different temperatures T=(10-2,10-3,0) (a) w+D and (b) ηcontrast vs the control-field Rabi frequency Ωd .Here Δ=90 MHz and δc=−Δ and others are the same as in Fig.2.

4.3 实验中原子能级和参数的选取

在倒Y 型模型中,实验上可选用87Rb 原子的能级结构: 两个超精细基态分别为|g〉=|5S1/2,F=2〉和|m〉=|5S1/2,F=1〉,激发态|e〉=|5P3/2〉和|r〉=|5D5/2〉构成倒Y 型四能级结构[16,30].另外,与能级寿命有关的自发衰减率是Γg=Γm=1 kHz,Γe=6.0 MHz[30],Γr=680 kHz[16],耦合光和附加控制光的失谐量分别为δc=−90 MHz,Δ=90 MHz[11].在实际实验中,可选取三束光场的拉比频率为Ωp=0.2 MHz[10],Ωc=2 MHz[16],Ωd∈(0.1−60)MHz[11].可以发现,当Ωd=6.6 MHz 和δ=90.12 MHz (探测光失谐量)时,有望获得兼具窄线宽w+D=23 kHz和高对比度ηcontrast=0.99的最佳吸收光谱线.

另外,在Ωd=3 MHz 和 6.6 MHz 两种情况下,通过大范围地调节附加光场的失谐量Δ发现,随着Δ的增大,谱线宽度w+D急剧减小.当Δ=900 MHz时线宽w+D可达 2.2 kHz,与理论预估的极限值2 kHz已非常接近.而失谐量Δ的变化对谱线的对比度没有明显影响,仍然保持在 0.99 左右.

5 结论

理论研究了倒Y 型四能级原子系统中探测光吸收谱线的窄化机制,解析推导了吸收光谱窄化的极限线宽.研究发现,通过附加第三束控制光场的有效调节,可以使得该线宽仅依赖于两个超精细基态之间的相干衰减率,远小于原谱线的自然线宽.与传统的三能级梯型结构相比,吸收光谱线宽的窄化极限值可以提高2 个数量级.通过适当调节控制光的拉比频率和失谐量,本文模型有望获得兼具超窄线宽 (约23 kHz) 和高对比度 (约0.99)的可观测光谱信号.在研究吸收谱线对光场的响应规律时发现,施加控制光可以有效地改善谱线的特征,获得兼具窄线宽和高对比度的吸收光谱线;但由于受制于基态能级间非常小的相干衰减率,导致响应时间较长.另外，还系统地研究了数值结果的依赖关系以及原子热运动对窄化的影响,虽然不满足无多普勒的波矢匹配条件,但可以通过优化光的传播方向减小多普勒效应的影响,在低温环境下获得较理想的窄化谱线.这些研究成果将为高分辨光谱的实验发展提供帮助.