储罐内爆碎片多相耦合计算方法与抛射轨迹研究
丁宇奇,卢 宏,芦 烨,谢 清,杨 明,张佳贺,刘凯
(东北石油大学 机械科学与工程学院,黑龙江大庆 163318)
0 引言
大型储罐通常存储易挥发、易燃、易爆物料,挥发出的气体与空气混合容易发生燃烧、爆炸,其爆炸后产生的巨大能量会导致储罐自身结构发生破坏,若罐体破坏后产生碎片将可能引发多米诺效应[1],对邻近储罐及建筑物造成破坏。因此,对储罐内爆破碎及碎片形成后的运行轨迹研究就显得尤为重要。
储罐内爆破碎问题主要涉及爆炸载荷、结构响应、碎片的形成以及抛射轨迹等方面。在爆炸载荷模拟方面,管义锋等[2]采用TNT当量法对燃气泄漏引发的爆炸事故进行分析,通过理论计算得到不同位置的冲击波超压以及危害后果,与实际爆炸后果一致;胡可等[3]采用CFD方法对大型储罐内甲烷/空气预混气体的爆炸过程进行模拟,得到了不同容积、可燃气体种类与浓度等因素对储罐结构爆炸载荷的影响。在爆炸载荷作用下的结构响应方面,金泽宇等[4]基于ALE流固耦合算法,对球壳在TNT炸药爆炸载荷下的结构响应开展研究,得到了流体的响应以及球壳的抗冲击性能;胡陈[5]考虑多相耦合作用,建立了拱顶罐爆炸数值分析模型,得到了炸药当量、炸药位置及液位对储罐结构动态响应的影响规律;DING等[6]以立式拱顶储罐为研究对象,采用有限元计算方法计算了储罐爆炸过程中流体的压力和温度,得到了储罐的应力和变形分布。在爆炸碎片形成的数值模拟方面,张志彪[7]以TNT炸药为爆源,通过以断裂应变控制的单元删除法,得到了壳体碎片分布,不过单元删除法会造成罐体材料的质量损失,而且破片数量也偏少;董新刚等[8]通过损伤模型控制材料的破坏,采用光滑粒子动力学(SPH)方法对TNT爆炸冲击作用下绝热挡环的破碎性能开展研究,获得了有无削弱槽结构的破碎开裂形式和碎片尺寸,但是光滑粒子法中产生的随机破片形态并不理想,无法确定大碎片的边界。在爆炸碎片抛射轨迹求解方面,钱新明等[9-10]采用蒙特卡洛方法对储罐爆炸碎片的抛射开展研究,得到了碎片的轨迹曲线、抛射距离的概率分布等。虽然蒙特卡洛方法模拟的结果与实际数据一致性较好,但该方法基于很多理想化的条件,如爆炸储罐被视为一个质点、忽略储罐的体积等,而且也无法定量揭示爆炸冲击对结构的动力响应以及碎片的产生过程;王文红[11]考虑流固耦合作用,通过理论估算方法得到碎片的抛射距离,定量分析了爆炸碎片的影响范围及在影响区域内对设备、人员造成的伤害程度。
综上,现有关于储罐内爆破碎研究中,还未充分考虑爆炸载荷与罐体之间的多相耦合问题,且不能准确刻画碎片产生后的形貌与质量。为此,以球形储罐为研究对象,考虑内爆流体-球罐(碎片)-罐外气体的多相耦合以及爆炸载荷的传递,建立球罐内爆三维有限元模型;基于指数内聚力失效准则建立储罐材料粘结单元的失效条件,既可准确刻画球罐内爆碎片的形成过程,又可保证内爆前后的质量守恒;通过与蒙特卡洛方法的对比分析,验证本文数值模拟计算结果的准确性,该研究成果可为储罐内爆事故预防与事故救援提供理论依据。
1 基于多相耦合的储罐内爆载荷传递与碎片轨迹计算方法
1.1 储罐内爆载荷传递方法
GUBINELLI等[12]综合分析了143宗储罐爆炸碎片抛射事故,得出卧式储罐事故数量最多,球形储罐次之。为此,本文以球形储罐为例开展研究,其内爆并产生爆炸碎片的过程如图1所示。罐内气体、罐内液体、球罐和罐外空气4个区域之间复杂的载荷数据需要通过耦合面实现传递,在球罐内爆过程中涉及了罐内气体-球罐、球罐-罐外空气、罐内液体-球罐等多个耦合界面。通过CEL[13](耦合欧拉-拉格朗日)方法对不同相之间的耦合关系进行描述,其中流体和结构之间采用通用接触算法,以达到计算中自动追踪结构与流体之间的耦合接触面的目的。
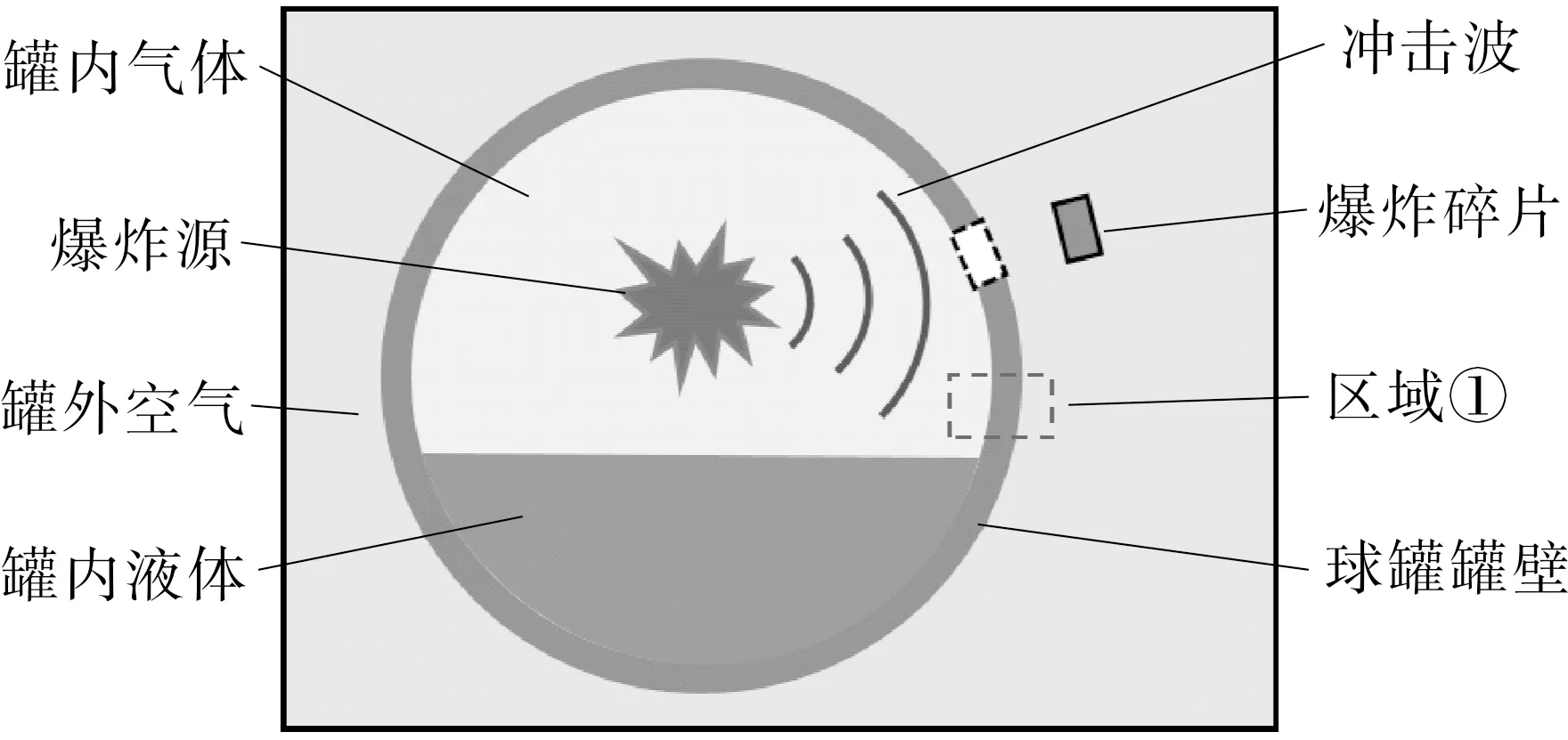
图1 球罐内爆过程示意
球罐内部可燃气体发生爆炸后产生的冲击波在罐内流体中传播,在图1中区域①位置,冲击波通过罐内气体-球罐耦合界面后作用到球罐结构上,球罐便发生变形破坏。球罐的响应一方面通过罐内气体-球罐耦合界面将变形等数据反馈给罐内气体,另一方面通过球罐-罐外空气耦合界面传向罐外空气。每个时间步流体与结构之间通过自动追踪的接触面传递数据,区域①中耦合界面的载荷传递如图2所示,(图中,虚线表示耦合界面变形前的位置,实线表示耦合界面变形后的位置)。
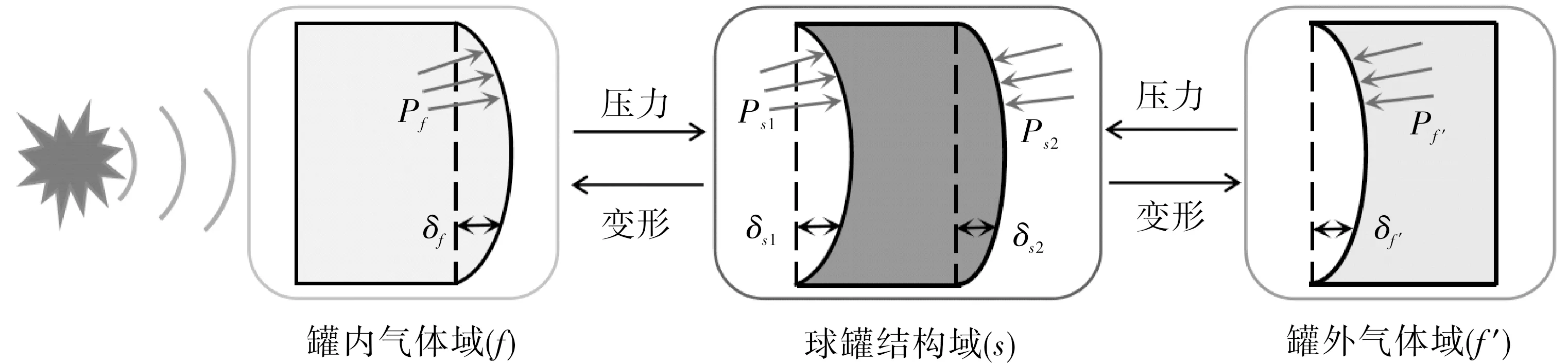
图2 球罐局部载荷传递示意
爆炸冲击波使罐内气体产生压力,该压力通过罐内气体作用在球罐结构上,如式(1)所示。
Pf=HfsPs1
(1)
式中,Pf为罐内气体压力向量,MPa;Hfs为罐内气体域到球罐结构域的传递矩阵;Ps1为球罐结构内表面的压力向量,MPa。
在球罐压力Ps1的作用下,球罐结构内表面产生变形并反馈给罐内气体,如式(2)所示。
δs1=Hfs1δf
(2)
式中,δs1为球罐结构内表面的位移向量,mm;Hfs1为球罐结构域到罐内流体域的传递矩阵;δf为球罐内表面变形后罐内流体边界处的位移向量[14],mm。
在球罐结构内表面变形δs1作用下,球罐外表面产生变形并传递到罐外流体域,如式(3)所示。
δs2=Hf ′s2δf ′
(3)
式中,δs2为球罐结构外表面的位移向量,mm;Hf ′s2为球罐结构域到罐外流体域的传递矩阵;δf ′为球罐外表面变形后罐外流体边界处的位移向量,mm。
罐外气体域的压力Pf′为大气压,直接作用到球罐结构外表面上,如式(4)所示。
Pf ′=Hf ′s2Ps2
(4)
式中,Pf ′为罐外气体压力向量,MPa;Hf ′s2为罐外气体域到球罐结构域的传递矩阵;Ps2为球罐结构外表面的压力向量,MPa。
1.2 爆炸碎片形成后的抛射轨迹研究
1.2.1 爆炸碎片运动轨迹的坐标变换
爆炸碎片产生后,随着爆炸能量的消耗,碎片的速度会达到一个最大值,将该时刻作为碎片抛射的初始时刻,此时碎片在空气中抛射的初始速度为v0。若仅考虑风阻对碎片轨迹的影响,碎片将在一个平面内运动,可将受阻力作用下的三维空间碎片抛射问题简化为二维平面问题,如图3所示。
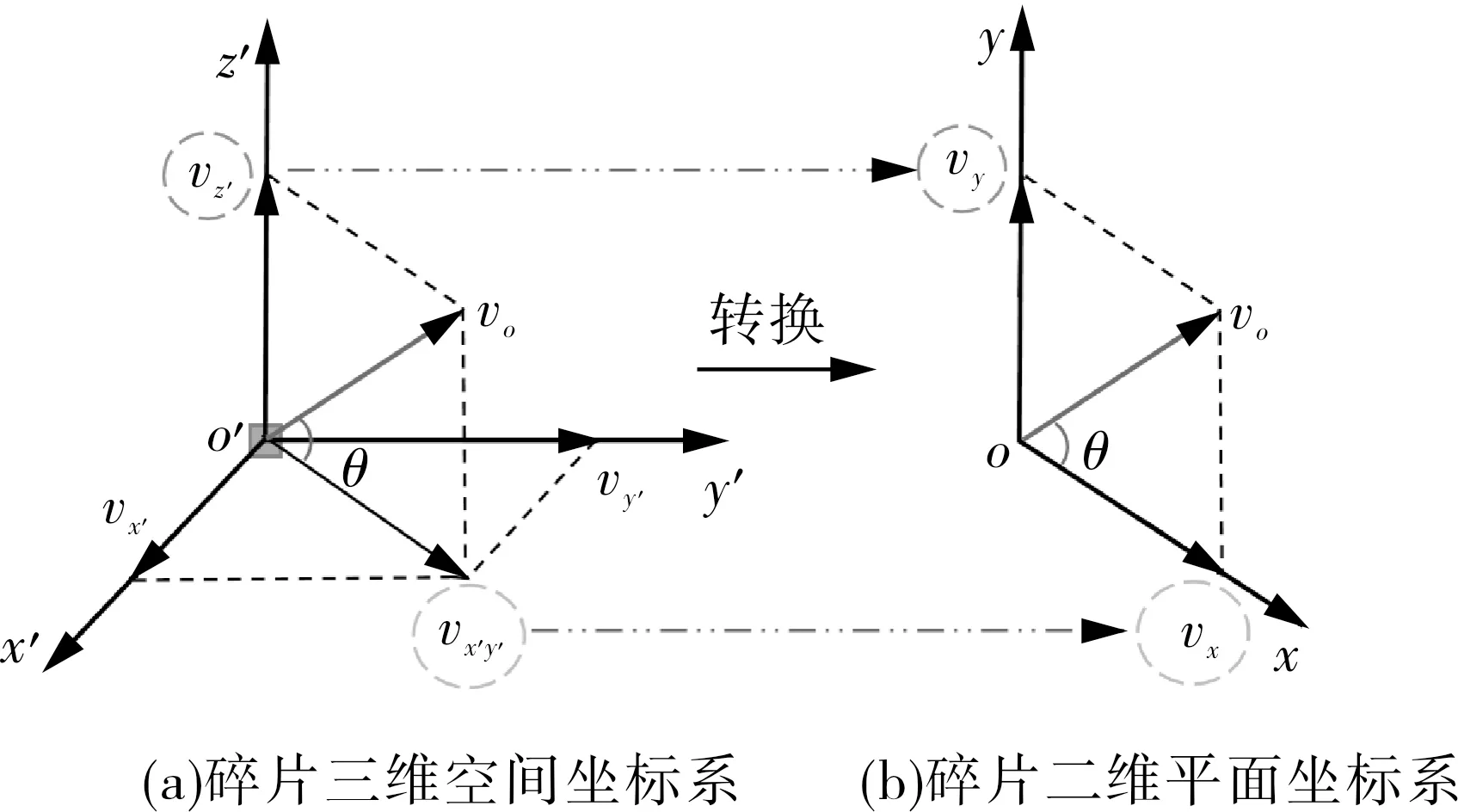
图3 碎片二维坐标系的转化过程
在三维空间坐标系中,vx′,vy′,vz′分别为v0在x′,y′,z′方向的分量;vx′y′为v0在x′o′y′面的投影。碎片在vz′,vx′y′所在平面内运动,将空间坐标系转换为该平面内的二维坐标系,其中vz′=vy,vx′y′=vx,以下在碎片二维平面坐标系中对碎片抛射轨迹进行求解。
1.2.2 局部坐标系下的碎片抛射
碎片在二维坐标系中的抛射情况如图4所示。在整体坐标系XOY中,初始时刻碎片坐标为(X0,Y0),为了便于计算,在初始时刻碎片位置处建立局部坐标系xoy;局部坐标系中,碎片初始速度v0,抛射角度为θ(θ在第一象限为正值,在第二象限为负值)。
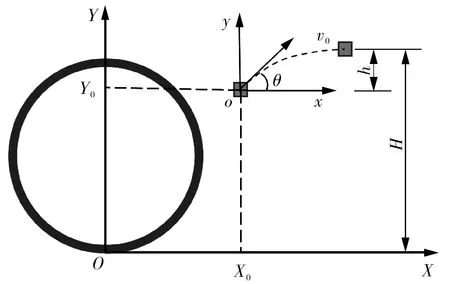
图4 二维坐标系下的碎片抛射
局部坐标系下碎片初始条件:
(5)
(6)
碎片在空气中运动总是会受到与速度成正相关的空气阻力影响,在考虑抛体速率较低时,可将空气阻力的大小近似为与速率成正比,即:
(7)
其中:
(8)
式中,k为比例系数;ρa为空气密度;S为迎风面积;C为空气阻力系数。
于是在二维坐标系中,碎片在空气阻力作用下的运动学方程可写为:
(9)
(10)
将初始条件式(5)(6)代入式(9)(10),解出碎片的运动学方程表达式为:
(11)
(12)
对式(11)(12)中时间t求导,得到碎片运动的速度表达式:
(13)
(14)
令式(14)等于零,得到碎片运动到最高点的时间为:
(15)
再将式(15)代入式(12),得到碎片的抛射高度为:
(16)
同时,由式(11)(12)可得碎片的轨迹方程:
(17)
1.2.3 球罐整体坐标系下的碎片抛射
在球罐整体坐标系XOY与碎片局部坐标系xoy之间存在如下关系:
X=X0+x,Y=Y0+y
(18)
将式(18)代入轨迹方程(17),得到球罐整体坐标系下的轨迹方程为:
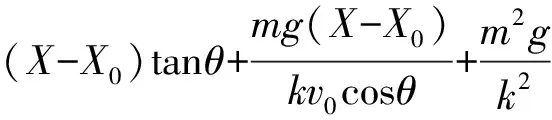
(19)
在球罐整体坐标系下,令式(19)中Y=0,可以得到碎片的抛射距离。同时,通过式(16)、(18)可以得到碎片的抛射高度为:
H=Y0+h
(20)
2 储罐内爆碎片破坏条件的建立
内爆引发的储罐破坏包含多种表现形式,其中剪切失效是材料在冲击载荷下与动态损伤演化-破坏相关的一个重要的失效形式,该现象普遍存在于高速撞击、高速成型等涉及爆炸与冲击的高速变形过程中,采用CFD计算方法可描述这种结构大变形、剪切效应明显的爆炸失效[15-16]。而储罐爆炸碎片的产生更倾向于小变形、极高应变率的材料失效,采用TNT当量法则可描述传播速度更快速的爆破过程。材料的破坏不是瞬间完成的,而是一个损伤积累的过程。本文选用指数内聚力模型对球罐材料的初始线弹性阶段和损伤后的应力软化阶段进行描述。有研究表明[17],指数内聚力模型能够较好地描述材料破坏过程中的能量耗散行为。
球罐受爆炸冲击波作用,当应力超过内聚强度σmax,材料就发生了损伤。在损伤阶段,材料基于指数内聚力模型的失效准则定义如下:
(21)
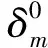
随着载荷的持续作用,损伤不断发展,当D=1时,材料完全损伤,这时球罐发生破坏。
为保证球罐内爆发生后罐体及产生碎片的质量守恒,采用在罐体材料中引入粘结单元的方法对内爆前后储罐碎片状态进行模拟。通过在罐体单元之间插入一层厚度很小的粘结单元,将罐体单元之间的直接联系转换为通过粘结单元间接联系,利用粘结单元的失效模拟罐体单元之间的分裂,爆炸碎片形成的过程如图5所示。
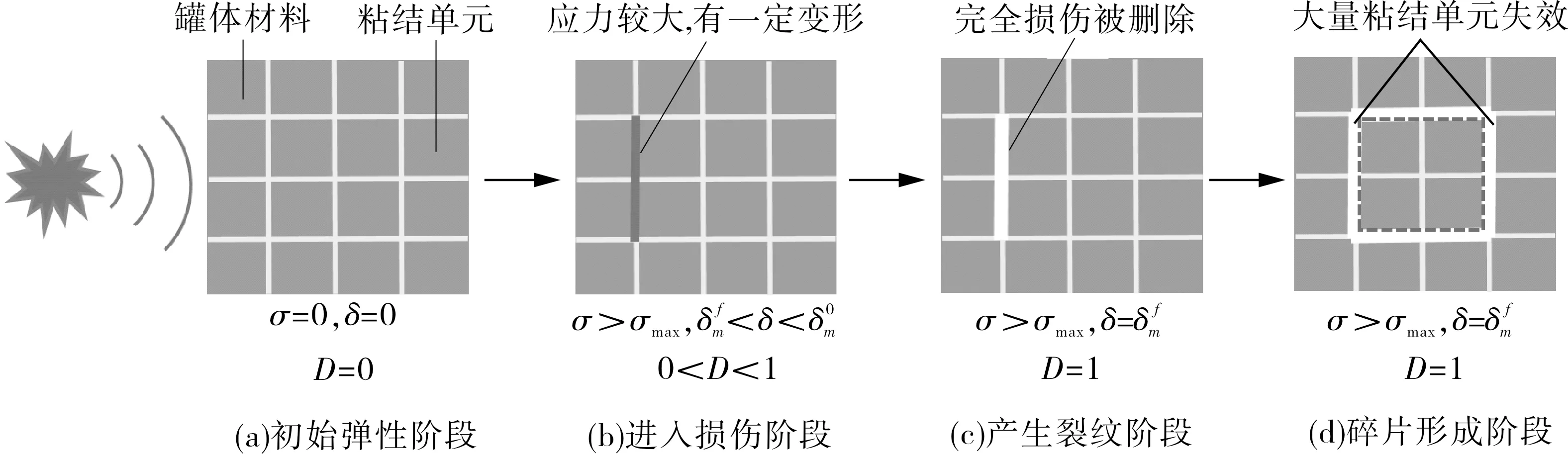
图5 储罐内爆碎片形成过程示意
在爆炸载荷作用下,粘结单元首先进入弹性阶段,应力与变形呈线性关系。应力不断增大,超过内聚强度σmax后,粘结单元进入损伤阶段,其承载能力不断降低,直至损伤参数D=1时,损伤完全,粘结单元因失去承载能力而被删除。少量的粘结单元被删除后,宏观上体现出来的就是球罐裂纹的产生,当大量粘结单元被删除且形成一个闭合的回路时,宏观上体现出来的就是球罐碎片的产生。这种间接的方法保证了罐体材料的质量守恒,更符合实际情况。
3 基于多相耦合的球罐内爆破碎过程数值模拟分析
3.1 球罐内爆数值模型的建立
以球形储罐为例进行分析,其结构如图6所示,其中球罐本体是球罐结构的主体,它是球罐储存物料承受物料工作压力和液体静压力的构件;球罐支柱是用于支承球罐本体重量和储存物料重量的结构部件,赤道正切柱式支座是使用最多的一种形式。本文模拟的球罐结构参数见表1。

图6 球罐结构示意

表1 球罐结构参数
采用Abaqus模拟平台进行建模以及计算,为了便于建模,将球罐简化为等壁厚的球壳,将支座对球罐的约束作用简化为罐壁上的约束条件。为了保证储罐结构响应、碎片飞射都在流体域内进行,建立包含球罐外部轮廓的空气域,罐外空气域尺寸为20 000 mm×20 000 mm×19 000 mm。由于模型的对称性,建立1/4球罐及空气域模型,如图7所示。
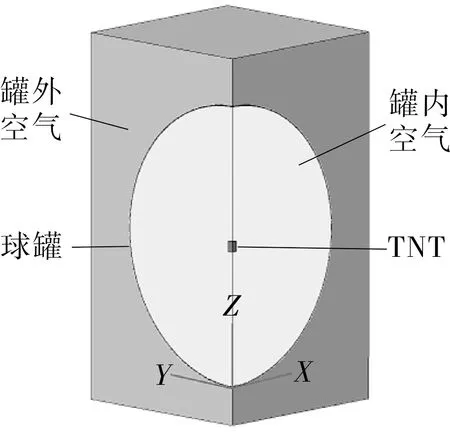
图7 球罐内爆几何模型
考虑到球罐内爆产生抛射碎片是个三维空间问题,所有模型采用实体单元进行离散,球罐用拉格朗日网格进行描述,TNT炸药与流体采用欧拉网格进行描述。球罐的三维有限元模型如图8所示,流体域的有限元模型如图9所示。对于球罐结构,在内爆过程中,只考虑内爆载荷和重力的影响,并将赤道正切柱式支座简化为支座与球罐接触位置处的完全固定约束。对于球罐内部流体域,在对称面(XZ平面、YZ平面)施加对称边界条件,其余表面施加无反射边界条件。储罐内气体燃爆载荷采用TNT当量法进行模拟[18],本文将TNT设置在球罐正中心处,并于计算开始时引爆。
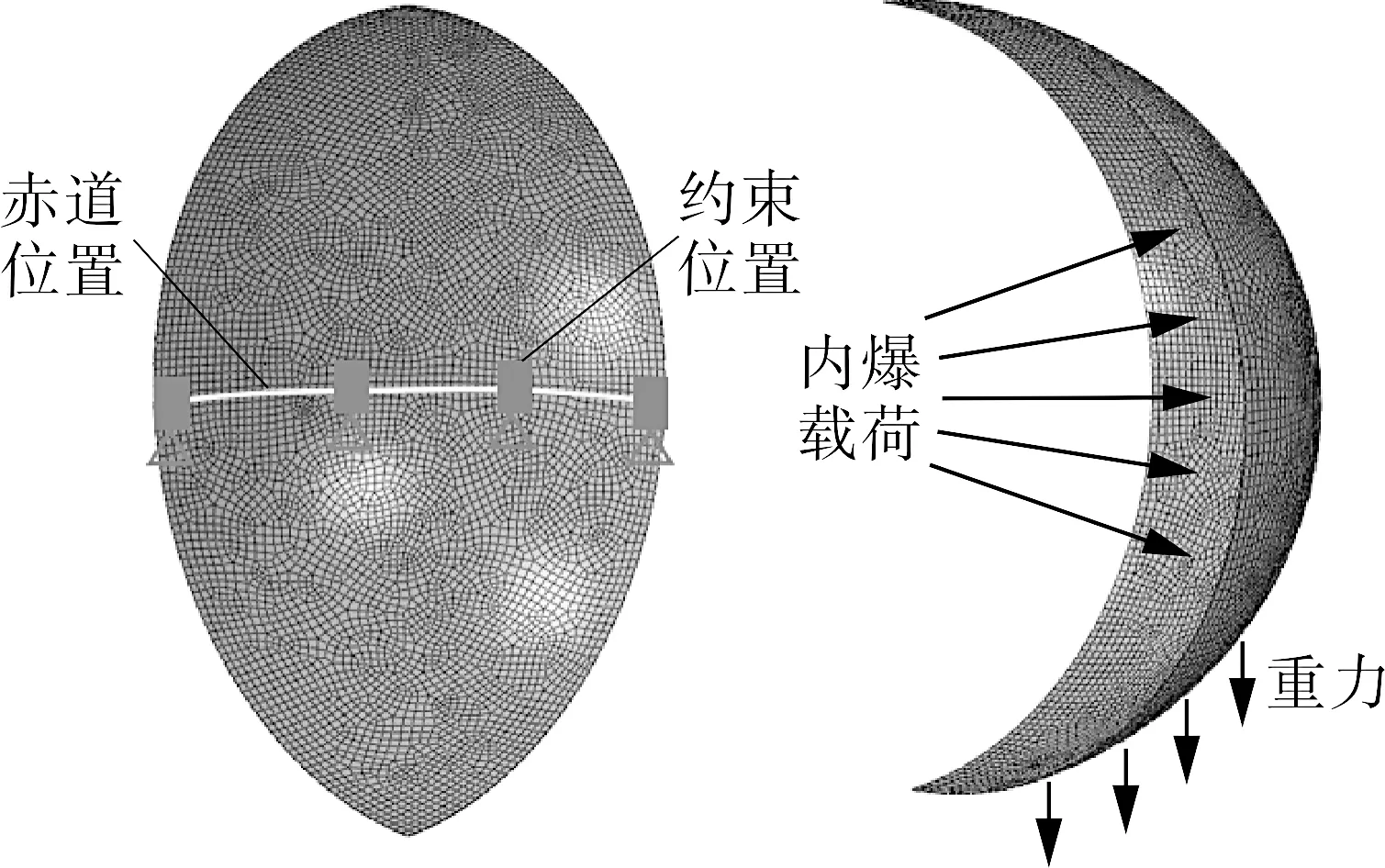
图8 球罐有限元模型
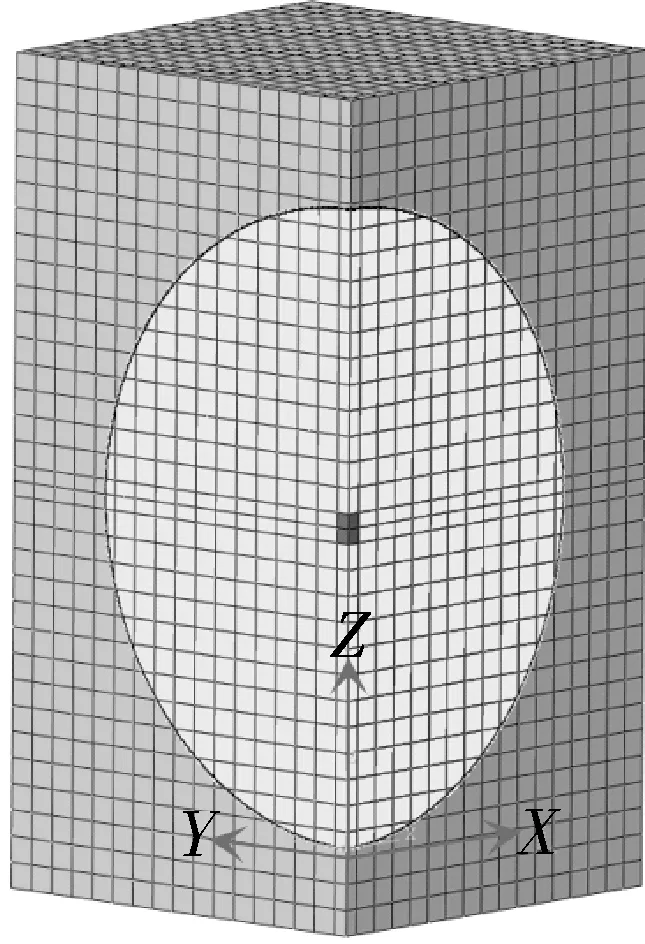
图9 流体域有限元模型
TNT炸药采用JWL状态方程来描述爆炸过程,其状态方程表达式为:
(22)
式中,PT为TNT爆炸压力,MPa;A,B,R1,R2,ω为TNT材料常数;E0为TNT初始比内能,J/kg;η为无量纲量,η=ρ/ρ0;ρ为爆轰产物密度,kg/m3;ρ0为炸药密度,kg/m3。
各参数具体数值见表2。

表2 TNT材料参数
在高速剧烈载荷下,球罐材料表现出应变率强化效应,故采用Johnson-Cook[19-20]强化模型来描述,其表达式为:
(23)
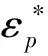
球罐材料采用Q345钢,其材料参数如表3所示。
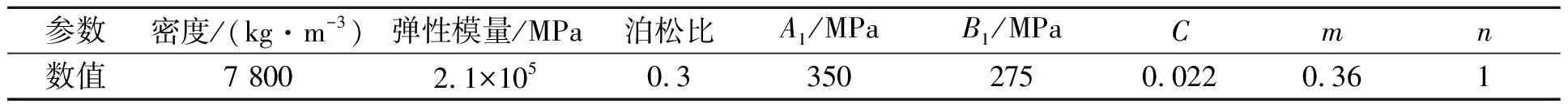
表3 球罐材料(Q345)参数
为了通过粘结单元的失效模拟球罐的破坏,粘结单元应采用与球罐材料相同的力学性能。由于断裂能、内聚强度以及失效位移等参数难以获得,因此参考了文献[21]中钢的部分材料参数,得到的粘结单元材料参数如表4所示。
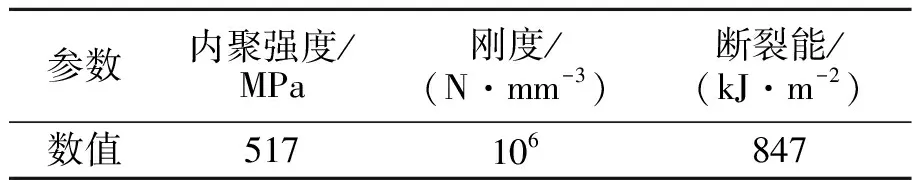
表4 粘结单元材料参数
罐内气体与罐外空气均可采用理想气体状态方程来描述:
Pg=(γ-1)ρgE1
(24)
式中,Pg为气体压力,MPa;γ为气体绝热系数;ρg为气体密度,kg/m3;E1为气体内能,J/kg。
3.2 球罐内爆数值模拟计算结果分析
对于容积为1 600 m3的LPG球罐,在空罐状态时,球罐下部残留少量的储液,球罐上部存在着大量的石油气和空气,其中石油气的主要成分为丙烷和丁烷。若忽略残余储液体积,在烷类气体浓度为8%时,罐内可燃气体TNT当量为528 kg。
3.2.1 球罐结构应力分布
当储罐材料应力达到内聚强度517 MPa后,罐体发生损伤并导致断裂失效。为了清晰地观测到球罐结构断裂过程,在爆炸发生后第5 ms(破坏前)、第6 ms(破坏后)以及第23 ms(出现明显裂纹)时的粘结单元状态以及球罐应力分布如图10所示。

图10 不同时刻球罐粘结单元状态及应力分布
在5 ms时,球罐结构完整且应力低于内聚强度;在6 ms时,应力超过内聚强度517 MPa,开始有粘结单元失效被删除,结合罐体的应力分布可以看出,粘结单元失效的位置罐体材料应力很小,球罐的这些位置已经发生断裂破坏,不过宏观上不是很明显;在23 ms时,罐体材料已经出现较多且明显的裂纹。在发生破坏后(第6 ms),不断有新的粘结单元失效被删除,因此球罐的应力稳定在略高于内聚强度的水平。
3.2.2 球罐结构速度分布
在爆炸发生23 ms后,随着球罐裂纹越来越多,第一个碎片形成。在爆炸载荷持续作用下,碎片数量越来越多,速度也越来越大。在82 ms时,已经不再有新碎片产生,此时碎片数量最多且碎片速度达到最大值。第一个碎片形成(第38 ms)以及碎片数量最多、速度最大(第82 ms)时球罐结构的速度分布如图11所示。
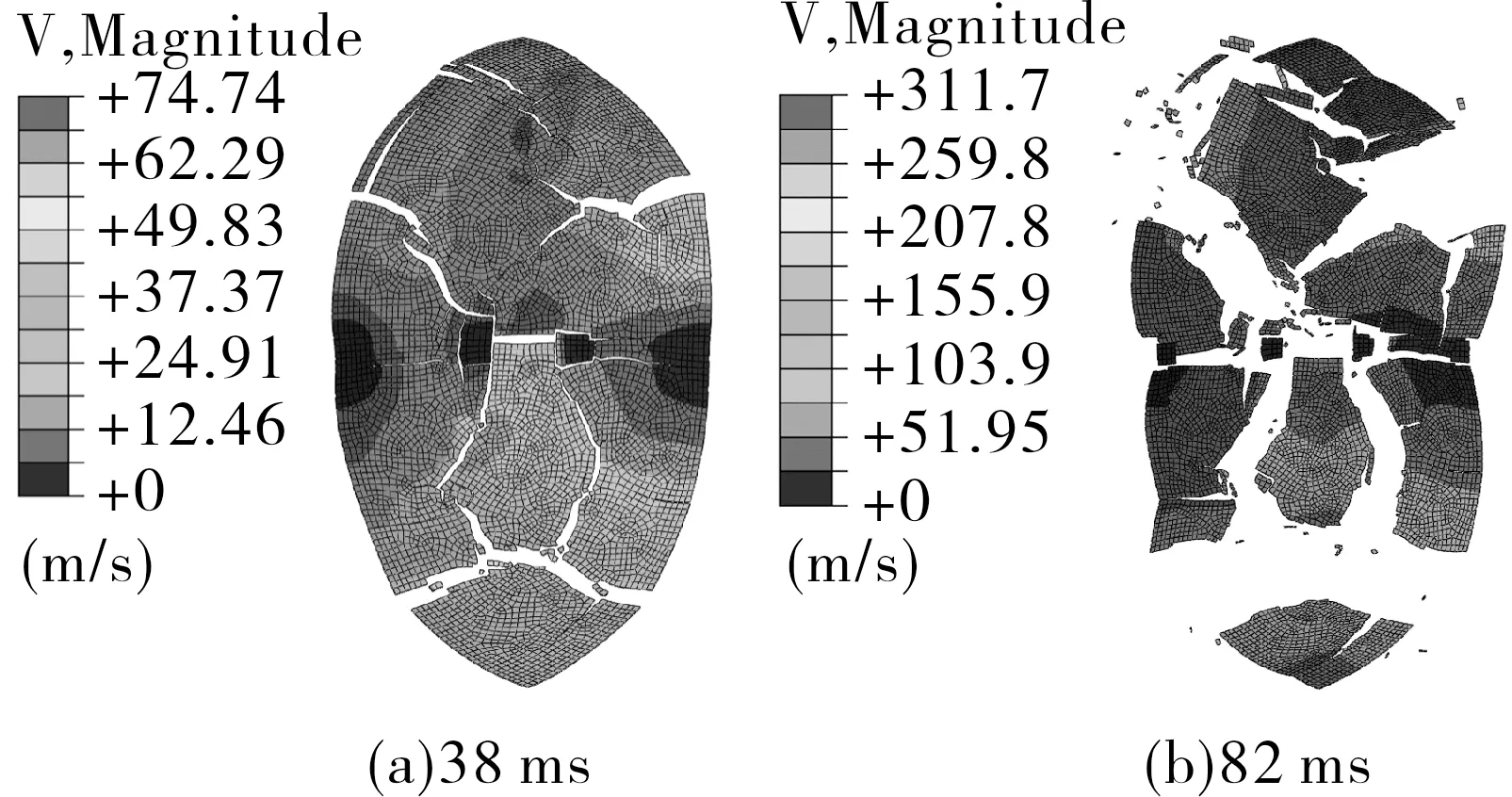
图11 不同时刻球罐碎片速度分布
3.2.3 碎片的形状、质量分布
经过统计,82 ms时共产生了6种不同形状的碎片,总数量为14个,每种形状碎片的速度分布如图12所示,碎片的初始速度和质量如表5所示。

图12 第82 ms时球罐碎片速度分布
通过表5中的数据可以看出,质量在3 000~5 000 kg范围内的碎片有8个,占碎片总数的57%;在10 000~20 000 kg的大质量碎片共6个,占总数的43%。总体来看,碎片的速度随着质量的增大而减小,但是碎片c、碎片d分别位于球罐正上方、正下方,受重力的影响较大,导致了位于正下方的碎片d速度更大。

表5 球罐碎片速度-质量统计结果
4 基于不同计算方法的内爆碎片形成与抛射轨迹对比分析
4.1 基于多相耦合的碎片抛射轨迹数值模拟分析
在82 ms时刻,二维平面坐标系中碎片b的初始状态如图13所示,碎片b的抛射轨迹计算过程如下。
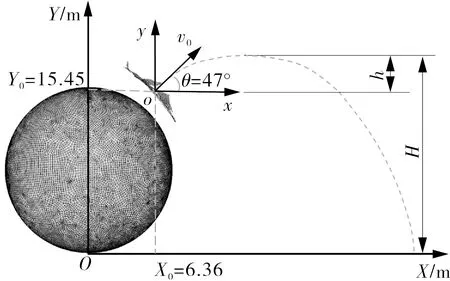
图13 第82 ms时碎片b初始状态
(1)通过数值模拟结果得到了碎片的初始位置坐标为(6.36,15.45),质量为4 563 kg,初始速度v0=72.4 m/s,抛射角θ=47°。
(2)选取与初始速度方向垂直的投影面,将碎片b向投影面投影后,得到碎片的迎风面积S=29.25 m2。空气密度ρa取1.25 kg/m3,空气阻力系数C取0.3[22],通过式(8)得到比例系数k=5.48 kg/m。
(3)在碎片轨迹方程式(19)中,令Y=0,可求得碎片b的抛射距离为548 m,通过公式(16)(20)得到球罐整体坐标系下碎片b的抛射高度H=157 m。
经计算,文中6种形状碎片的最终抛射高度、抛射距离如表6所示,各碎片可能的抛射轨迹如图14所示。
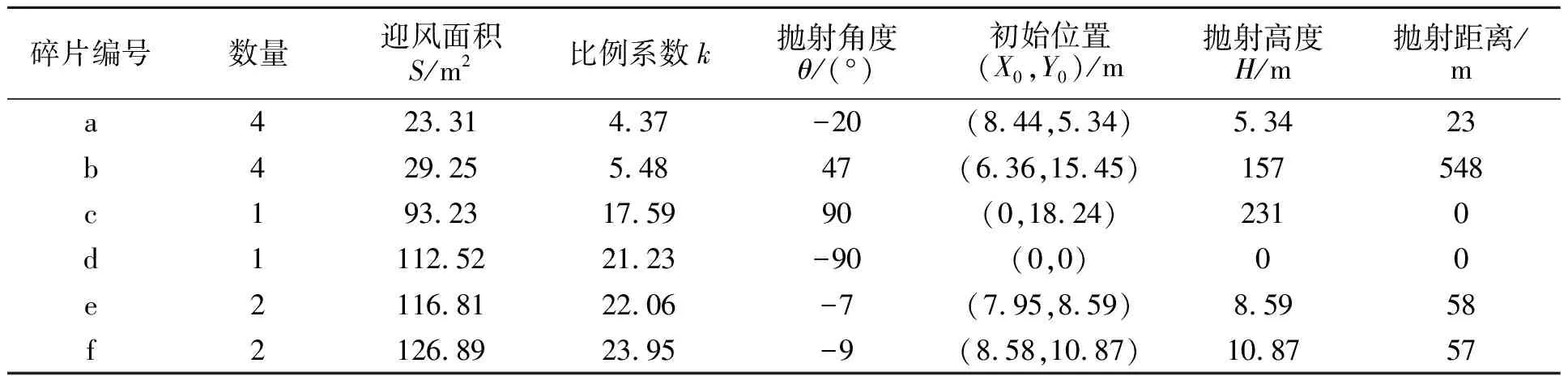
表6 碎片信息统计
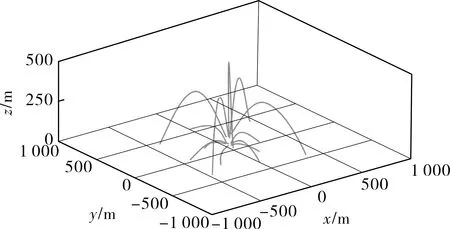
图14 碎片可能抛射轨迹
通过表6和图12可以看出,在球罐爆炸中,a,d,e,f四类碎片向下抛射(θ为负值)共有9个,占总数的64%;b,c两类碎片向上抛射(θ为正值)共有5个,占总数的36%。在向下抛射的碎片中,抛射高度为碎片的初始高度,抛射距离最大为58 m。对于向上抛射的碎片,c类碎片竖直向上抛射,所以抛射高度最高为231 m,抛射距离为0;b类碎片抛射角度为47°,抛射距离最大为548 m,抛射高度较高,为157 m。对比各类碎片的信息可以发现,向下抛射的碎片抛射高度和抛射距离都比较小;向上抛射的碎片抛射角度θ越大、抛射高度越高;向上抛射且抛射角度θ在45°附近的碎片,抛射距离最远。
4.2 基于蒙特卡洛理论求解的碎片轨迹计算
蒙特卡洛计算方法以概率和统计理论为基础,将所求解的问题同一定的概率模型相联系,通过大量的模拟统计以获得问题的近似解。文献[24]采用蒙特卡洛方法对1 600 m3球罐爆炸碎片的抛射轨迹进行了计算,并通过与实际事故数据相比较,验证了蒙特卡洛方法的有效性。
4.2.1 碎片的能量与速度
在蒙特卡洛方法中,储罐爆炸总能量通过式(25)计算,然后通过式(26)(27)得到碎片获得的动能Ek和碎片的抛射速度vp。
(25)
Ek=Efk
(26)
(27)
式中,p0为环境压力,MPa;p1为爆炸压力,MPa;γ为气体绝热指数;VS为储罐体积,m3;fk为能量转化效率;m为碎片质量,kg。
根据文献[22]中沸腾液体扩展为蒸气云爆炸(BLEVE)事故球罐的参数,其爆炸压力为1.34 MPa,绝热指数为1.4,爆炸压力p1在区间[0.9p1,1.1p1]内均匀分布时,通过式(25)计算得出爆炸总能量为2.61×109~3.32×109J。能量转化效率fk在区间[0.2,0.5]内右三角分布,按照fk=0.2计算,碎片总动能为5.22×108~6.64×108J,碎片的初始速度分布在84~95 m/s之间。
4.2.2 碎片的抛射轨迹
当碎片数量、抛射角度等随机参数已知后,采用蒙特卡洛方法对不确定参数进行大量的随机抽样,并代入碎片抛射轨迹方程(17)中。球罐爆炸100次的碎片轨迹空间分布情况如图15[24]所示,可以看出,球罐爆炸碎片的最大抛射高度为263 m,最大射程为600 m。
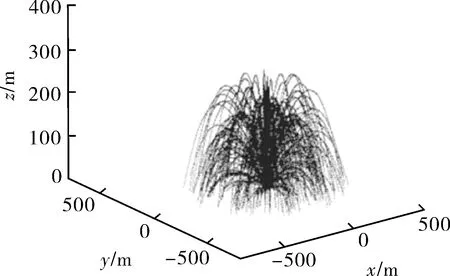
图15 100次模拟碎片轨迹
4.3 不同计算方法碎片结果对比分析
为了验证本文多相耦合计算方法的正确性,同时突出多相耦合计算方法的优势,将多相耦合计算方法的结果与文献[23]中蒙特卡洛计算方法的结果进行对比,两种方法中碎片数量、质量、能量等碎片初始信息对比如表7所示。
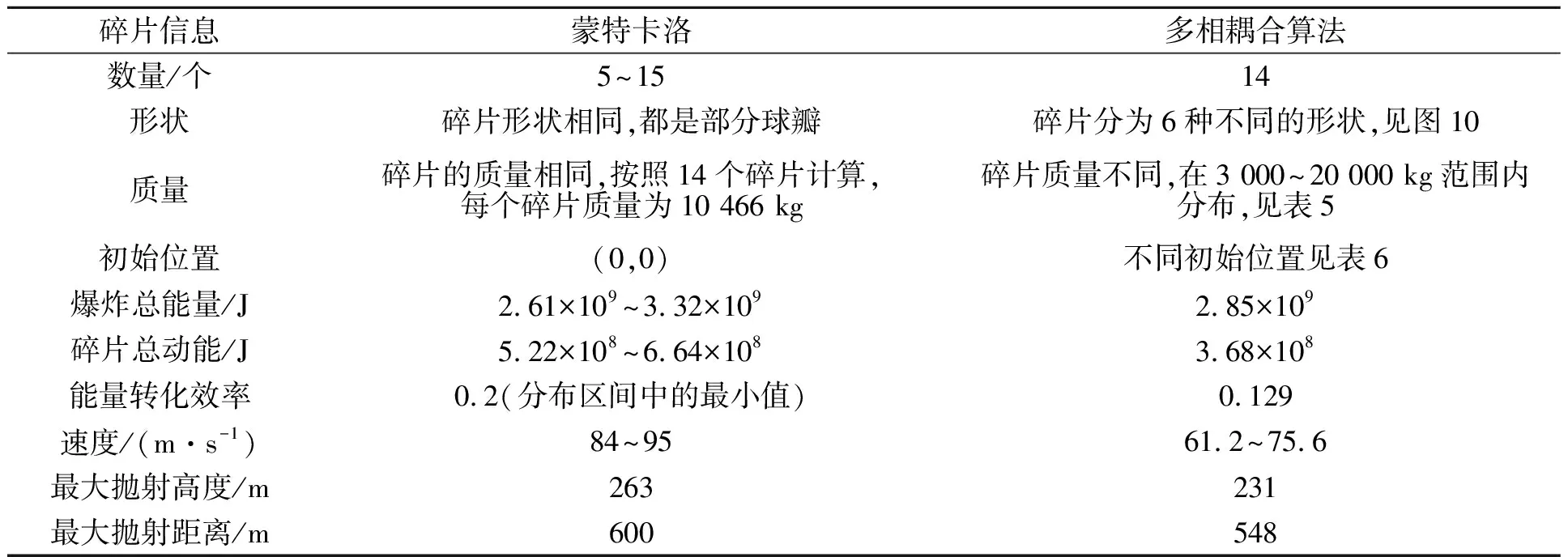
表7 不同计算方法碎片初始信息对比
由表7可以看出,在碎片的数量、形状和质量方面,蒙特卡洛方法都基于一些基本假设,不能具体描述碎片的差异性,而多相耦合方法得到了碎片的明确数量、质量以及具体形状。在实际中,碎片的数量、形状和质量具有随机性和特异性,而相比之下,多相耦合方法更有优势。文献[23]忽略了球罐的体积,假设所有碎片从同一位置出发,而多相耦合计算结果可以考虑球罐的体积,进而得到碎片不同的初始位置。
对于爆炸总能量,蒙特卡洛方法中为2.61×109~3.32×109J,由于爆炸压力p1在一定范围内分布,导致得到的结果范围较大;多相耦合方法得到的总能量为2.85×109J,在蒙特卡洛方法得到的结果范围之内。按照能量转化效率为0.2计算,蒙特卡洛方法中碎片总动能为5.22×108~6.64×108J;多相耦合中碎片总动能为3.68×108J,能量转化效率为0.129。相比之下,多相耦合计算方法的能量转化效率比蒙特卡洛方法中的最小值偏小35.5%。有研究表明[24],能量转化效率越低其概率越高,能量转化效率在0.14以下占89.6%,显然文献[23]中总能量转化为碎片动能的效率fk取值偏大,多相耦合方法中的能量转化效率更符合实际。
由于文献[23]蒙特卡洛方法中碎片动能偏大,导致碎片的初始速度偏大,直接影响了碎片的抛射高度和抛射距离,结果偏保守。与蒙特卡洛的结果相比,多相耦合中碎片抛射高度偏小12.2%,抛射距离偏小8.7%。
综上所述,蒙特卡洛方法选用的不确定参数都在一定范围内分布,也就是包含了碎片抛射过程中的所有可能性,因此在模拟爆炸碎片的分布概率上更有优势,但同时也导致了抛射距离、抛射高度等范围偏大,结果偏保守。而采用多相耦合计算方法在得到球罐动态破碎过程的同时,还能准确得到碎片的数量、速度、抛射距离等信息,所以在一个具体的球罐内爆碎片抛射问题上,多相耦合计算方法更精准、更有优势。
5 结论
(1)以球形储罐为研究对象,考虑罐内气体-球罐(碎片)-罐外空气的多相耦合以及爆炸载荷的传递方式,采用CEL流固耦合算法建立球罐内爆多相耦合有限元模型,基于指数内聚力模型建立损伤失效准则,将罐体单元之间的直接联系转换为通过粘结单元联系,并通过粘结单元的失效删除间接描述球罐材料的破坏,保证了球罐材料破碎前后的质量守恒。
(2)基于多相耦合的计算方法得到了球罐不同时刻的结构响应以及碎片的具体数量、形状、质量和速度等。考虑碎片不同初始位置以及空气阻力的影响,通过理论计算方法得到碎片的抛射轨迹和最大抛射距离。对比蒙特卡洛方法,多相耦合计算方法中能量转化效率比蒙特卡洛方法中的最小值偏小35.5%,碎片的最大抛射高度偏小12.2%,最大抛射距离偏小8.7%。
(3)在空罐状态下对1 600 m3球罐的多相耦合内爆模型进行计算,在82 ms时,已经不再有新碎片产生且碎片速度达到最大值,经统计此时碎片的数量为14个;质量在3 000~5 000 kg范围内的碎片占碎片总数的57%,在10 000~20 000 kg的大质量碎片占总数的43%;爆炸总能量到碎片动能的能量转化效率为0.129;碎片速度在61.2~75.6 m/s之间分布;碎片最大抛射高度为231 m,最大抛射距离为548 m。

