乏燃料贮运容器辐射传热特性影响因素分析
龙 腾,熊光明,章贵和
(中广核工程有限公司 核电安全监控技术与装备国家重点实验室,广东深圳 518172)
0 引言
乏燃料贮运容器依靠辐射、传导和对流耦合传热机制将衰变热传递至大气环境。容器表面的辐射传热为对外传热最主要的传热机制[1-3],因此辐射传热的准确模拟对乏燃料贮运容器传热分析至关重要。目前,工程上采用下述两种方法模拟乏燃料贮运容器的辐射传热:一是基于半经验公式确定壁面的辐射和对流的换热系数[4],作为边界条件施加到单一热传导机制的计算模型[5],此经验公式适用于特定的坏境条件和壁面结构,但需进一步验证才能应用于乏燃料贮运容器;二是基于传导-对流-辐射耦合的计算模型精确模拟乏燃料容器内外部流场的换热机制。笔者团队[1-2,6]对容器内外部自然对流算法及容器结构优化进行了研究,较准确地模拟了容器的对流和传导的耦合传热效应,但在辐射传热分析中采用了确定性的辐射参数,未考虑辐射参数在某一区间内取值,且未对辐射参数的选取进行深入分析。
事实上,物体的辐射发射率作为辐射传热的关键参数[7],取决于物体的材质、表面粗糙程度、表面几何形状、波长以及表面温度等因素,根据公开文献对发射率的测量结果,该数值常在一定区间内波动[8-11]。选取过大的发射率意味向外辐射能量越多,与此同时吸收太阳辐照的能量也越多。上述乏燃料贮运容器热工分析未考虑辐射参数的不确定性,国内外也未见辐射关键参数对乏燃料容器各部位温度分布的影响研究,如何选取合适的发射率是该容器热工分析的关键问题。
本研究是在前期乏燃料贮运容器热工分析的基础上[1-2,6],采用传导-对流-辐射耦合CFD模型,进一步对辐射传热关键参数进行分析,展开对乏燃料贮运容器在太阳暴晒下辐射关键参数的研究,探索不同环境条件、不同壁面发射率、不同外部环境发射率对传热性能的影响,从热工角度为结构优化设计提供技术参考。
1 分析模型
1.1 物理模型
该设备本体由高约4.5 m、直径约3 m、壁厚约0.4 m的容器筒体、燃料篮和燃料组件组成,如图1所示。容器表面为环型肋片状结构,用于增大容器表面积,加强对外散热能力。燃料篮位于填充氦气的容器内腔之中,主体材料为不锈钢,焊接形成多组可供存放乏燃料组件的格架,格架表面附有铝基碳化硼。燃料组件为容器的唯一热源,通过燃料篮、氦气以及容器筒体往大气传热。
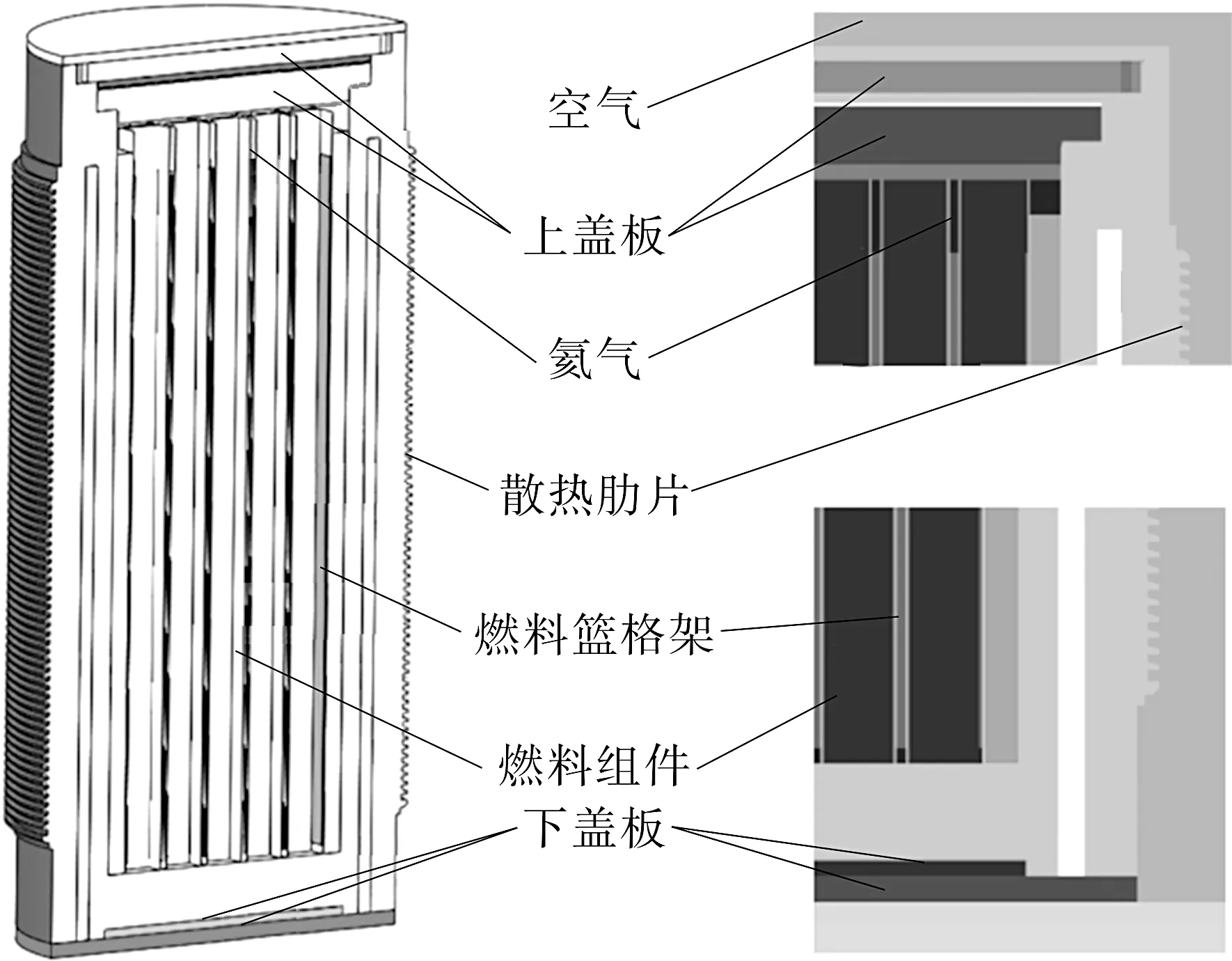
图1 乏燃料贮运容器几何模型
传热物理过程包括:燃料组件内部通过辐射、对流和传导耦合模式将衰变热传递至燃料篮;燃料篮格架及其周边的氦气通过辐射、对流和传导耦合模式将热量传递至容器筒体内表面;以及容器筒体内表面的热量传导到外表面(包括圆柱体容器侧面(含肋片)和顶面)后,通过辐射和对流模式往大气散热。
根据前期研究,基于Non-Boussinesq模型的高温差自然对流传热精度较高[1-2],而辐射传热与表面发射率、辐射角、外部太阳辐照工况等关系密切,高精度的辐射模拟对传热分析的结果影响明显。
1.2 辐射模型
乏燃料贮运容器CFD模型包括由燃料组件、燃料篮组件、筒体构成的多固体域以及内部填充氦气和外部大气构成的多流体域所构成,计算采用流固热耦合的等效导热模型、Non-Boussinesq模型模拟传导和对流机制,乏燃料容器需考虑表面对辐射的吸收、反射、散射等现象,采用离散坐标(Discrete Ordinates,DO)模型模拟辐射传热过程。该模型将辐射传热方程沿各个立体角进行离散,得到空间坐标系下的辐射强度的输运方程:
(1)
假设壁面服从Kirchhoff灰体辐射定理,即壁面发射率简化为等于吸收率,且发射率与波长无关。设置材料发射率和吸收衰减系数来设定吸收系数、反射系数和光学厚度。壁面发射率通过红外热像仪测定。氦气和空气假设为热辐射透明气体,固体为无透射材料。
2 数值模拟计算设置
2.1 几何模型及简化
容器内部燃料格架间填充氦气,依靠传导-对流-辐射等机制耦合传热;容器外部大气作为最终热阱,依靠对流和辐射排出热量。为模拟多重传热机制下乏燃料贮运容器传热过程,建立了筒体、燃料篮、燃料等固体域和氦气、空气等流体域组成的1/2对称CFD模型,考虑精度和计算效率,燃料组件采用等效多孔介质模型进行模拟[2],无需建立详细模型(下文所述容器内部不包含燃料组件内的详细结构)。忽略对传热影响较小的结构,如吊耳、密封螺栓等。外部空气域的外表面设为压力出口,表压设为0 MPa;空气域的底面和容器的底面与底面接触,保守设为绝热边界,分析几何模型和边界条件如图2所示。
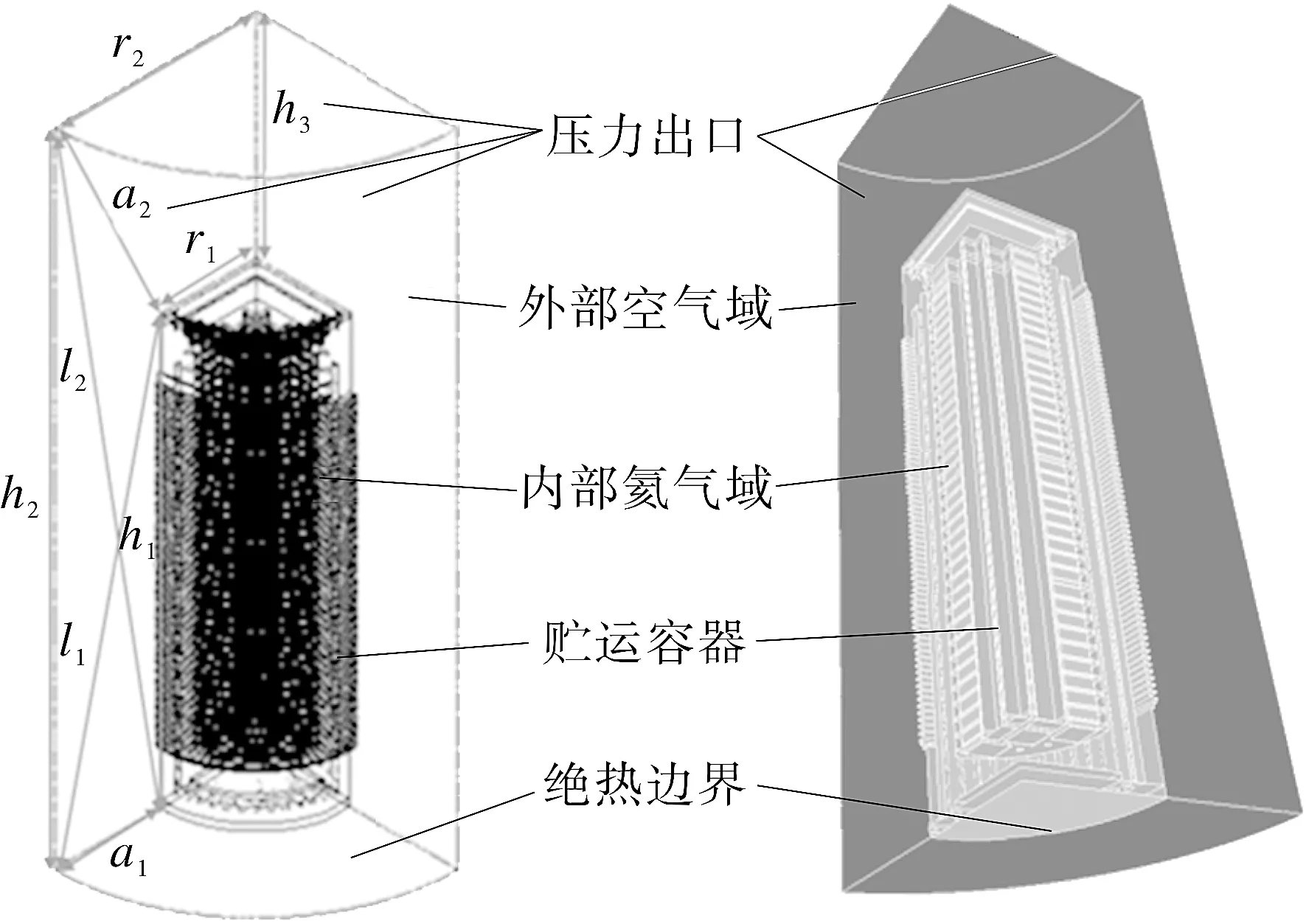
图2 简化模型及边界条件
2.2 基础设置
正常贮存潜在热源包括燃料衰变热和太阳暴晒。衰变热在燃料组件区域通过UDF设置“中间高、两端低”的体积热源;太阳暴晒以辐射的方式加热筒体外壁面,依据灰体假设,考虑24 h平均功率和发热率对吸收效率的影响,采用体功率方式施加在容器顶部和侧面的外壁面镀层上。太阳暴晒体发热功率为:
(2)
式中,ε为筒体侧表面发射率;P为侧面热功率为12 h日照辐射强度;l为镀层厚度。
采用DO模型并考虑容器内部的辐射传热,筒体、燃料和燃料篮之间的间隙形成封闭的氦气域,耦合面设置相应材料的发射率。容器外壁面的发射率设置为涂层的发射率;容器外部空气边界采用压力出口边界条件,设置回流温度、压力以及外部环境发射率;接触厂房地面的容器底部保守设为绝热边界,边界条件如图2所示。
容器内部氦气处于高温差密闭空间,流体流经复杂边界(拐角、台阶)位置会出现漩涡,流动状态十分复杂;容器外部表面温度接近100 ℃,近壁面空气为自然对流湍流状态。二者无法用简单的层流模型描述。为模拟容器内外部自然对流流动,根据NB/T 20462—2017《压水堆乏燃料干法贮存设施热工分析》,湍流模型选用RNG-k模型,壁面函数取Scalable函数。
网格无关性通过分别加密外部空气域网格和容器网格(含内部氦气域)来验证。首先开展外部空气域网格无关性分析,通过建立80万~140万4种外部空气域网格,容器网格保持1 100万不变,分别提取燃料组件、燃料格架、侧表面和顶面的最高温度,如图3(a)所示,确定外部空气域网格数为120万,用于后续容器内部网格无关性分析。然后分别建立600万~1 500万4种容器网格,结果如图3(b)所示,确定容器网格数为1 100万。因此,最终使用外部空气域网格和容器网格组成的总网格数为1 220万的网格开展后续分析。近壁面网格厚度无量纲数Y+≈40,处于要求的30~100的范围内。当容器向外传递能量功率等于热源总功率时,认为计算达到收敛。
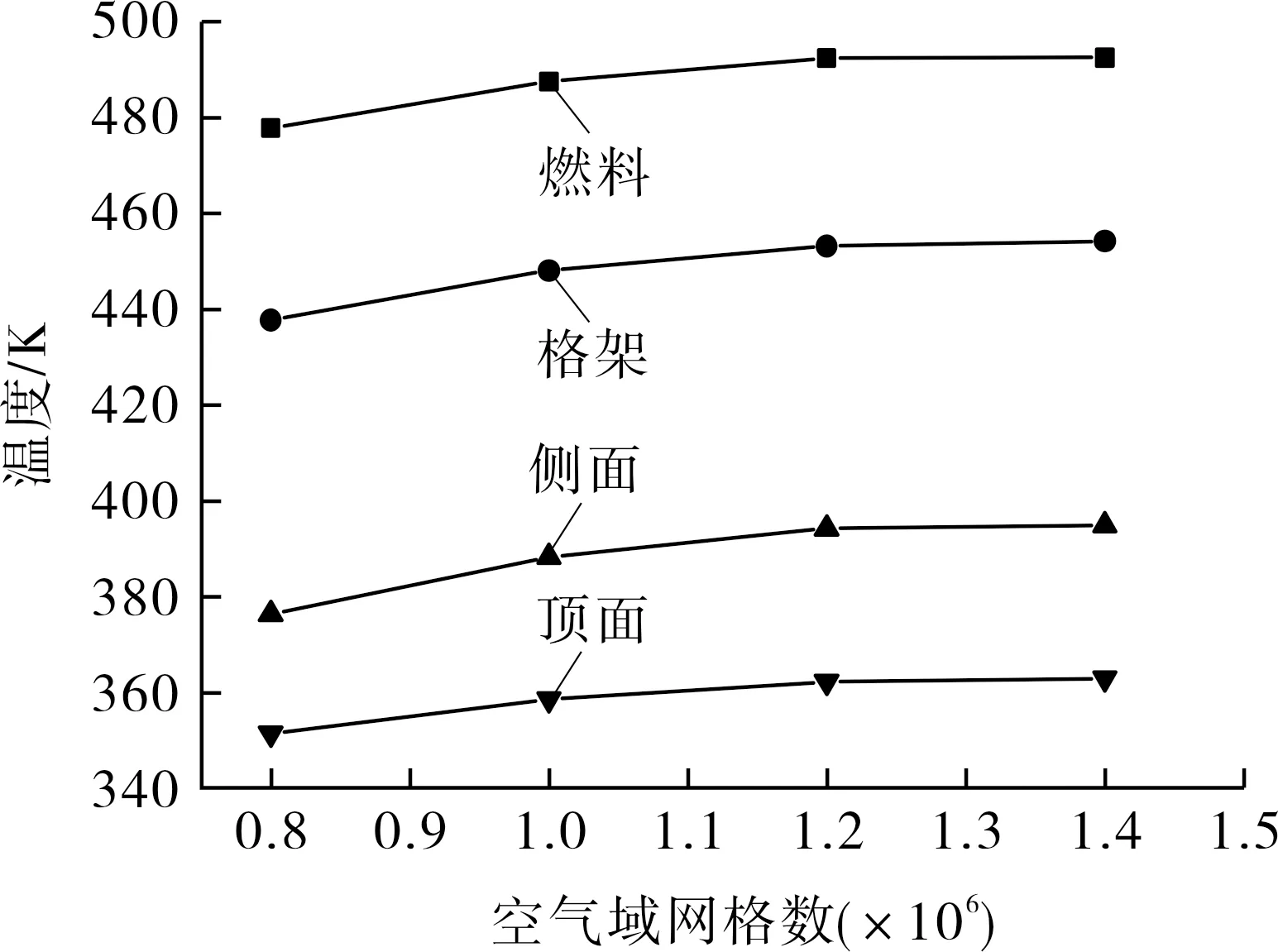
(a)外部空气域
2.3 发射率设置
发射率采用红外热像仪进行测量。首先在热像仪中输入大气参数、环境温度、被测物体表面温度,并设置红外热像仪发射率为1,得出热图像温度;再利用热像仪测温原理,计算出热像仪探测到的总辐射发射率,进而计算出被测物体表面发射率。根据公开文献数据[7-10],不同材质、表面处理工艺、环境等因素下主要区域发射率结果如表1所示。后续基于该结果开展表面发射率对容器传热特性的影响分析。
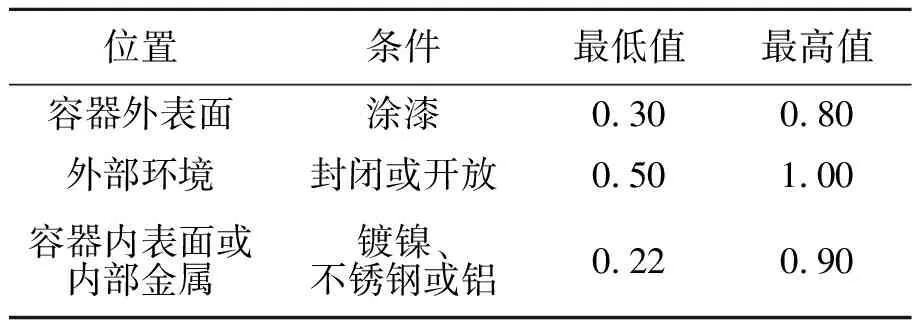
表1 主要材料的辐射发射率
3 结果分析
3.1 容器外壁面发射率对传热特性的影响
无暴晒和有暴晒条件下,外壁面发射率对传热的作用方式不同:无暴晒下,外壁面发射率仅影响容器对外部环境的辐射释放功率;有暴晒下,外壁面发射率同时影响释放功率和对太阳辐射功率的吸收功率,但作用效果相反,因此,无法定性给出外壁面发射率和容器各部位温度的关系。
为定量分析外壁面发射率对容器传热特性的影响,分别在无暴晒和有暴晒下,选取表2的工况1,2,3,分别设置外表面发射率为0.80,0.50,0.30。
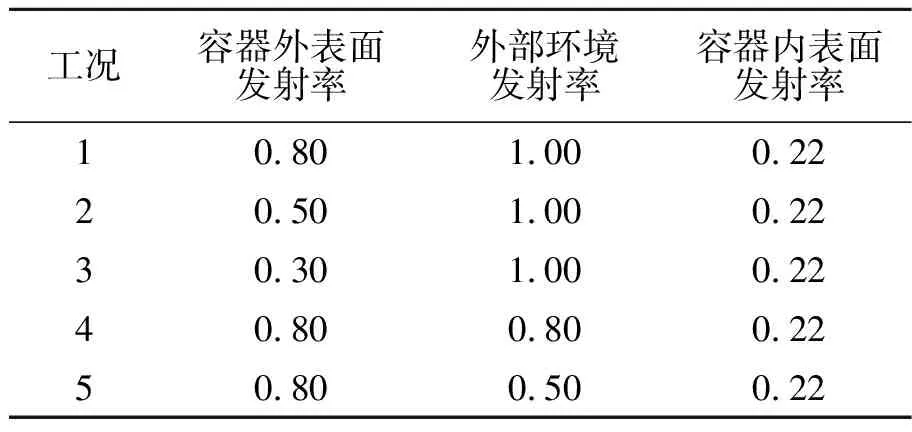
表2 DO辐射模型分析工况
3.1.1 无暴晒下容器外壁面发射率对传热特性的影响
无暴晒下,不同外壁面发射率引起的温度变化见图4和表3。当外壁面发射率增加时,外壁面向外部环境辐射功率将增加,为保证该功率与衰变热功率一致,外壁面和燃料包壳的温度将相应减小。
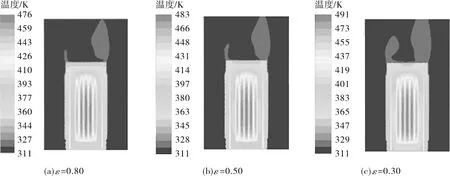
图4 无暴晒下外壁面发射率对容器各部位温度影响(内表面发射率=0.22,环境发射率=1.00)
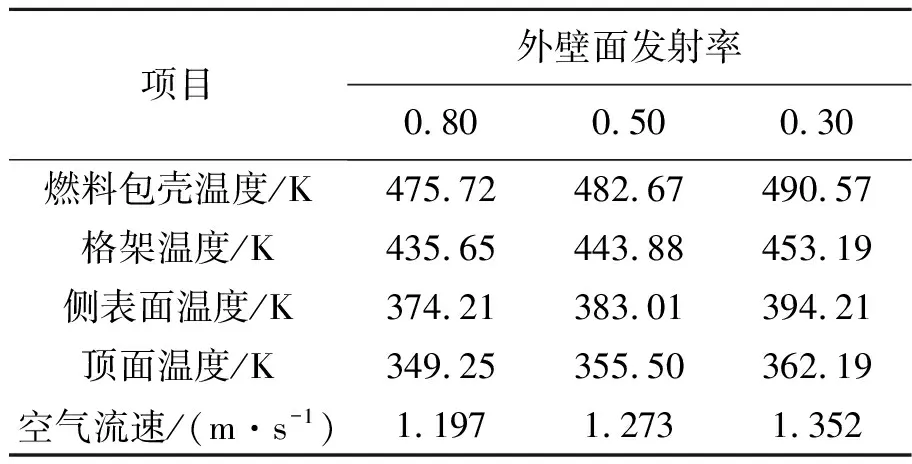
表3 无暴晒下不同外壁面发射率的最大温度及流速
外壁面发射率对外部环境空气自然对流速度的影响见图5。外部空气受翅片的阻碍作用而流速较低,最高流速位置出现在筒体顶部的流动分离位置。当外壁面发射率增加时,由于外壁面温度降低,导致外部空气流速也降低。
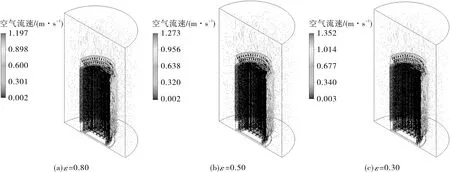
图5 无暴晒下外壁面发射率对空气流速的影响(内表面发射率=0.22,环境发射率=1.00)
无暴晒下,不同外壁面发射率下传热功率如表4所示。当外壁面发射率大于0.50时,容器向外传热方式中辐射占主导;当外壁面发射率为0.30时,辐射功率显著降低,传热方式以对流为主。
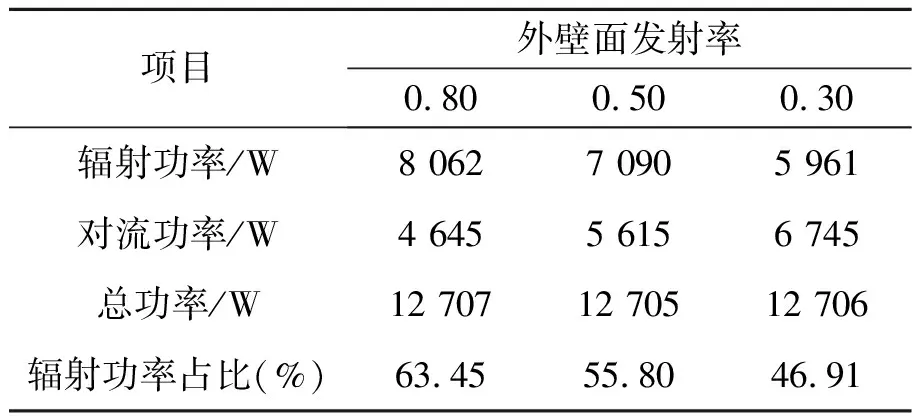
表4 无暴晒下不同外壁面发射率的传热功率
3.1.2 有暴晒下容器外壁面发射率对传热特性的影响
发射率越高,容器对外散热功率越高,但同时吸收太阳辐射功率也越高,二者又相互影响,因此有必要研究二者的相互关系。有暴晒下外壁面发射率对容器各部位温度影响如图6,7所示。
分别对比图4和图6、图5和图7,相比无暴晒工况,考虑暴晒后,由于衰变热叠加上太阳暴晒,使得整体热源功率变大,因此容器各部位温度及外部空气流速都呈现增加的趋势。容器外壁面发射率从0.30增加至0.80,无太阳暴晒工况的燃料包壳最高温度变化幅度是有太阳暴晒工况的3.51倍。
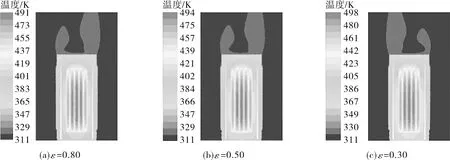
图6 有暴晒下外壁面发射率对容器各部位温度的影响(内表面发射率=0.22,环境发射率=1.00)
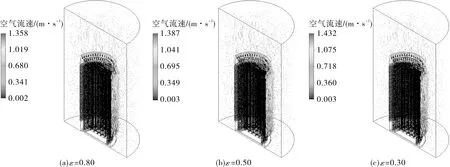
图7 有暴晒下外壁面发射率对空气流速的影响(内表面发射率=0.22,环境发射率=1.00)
综合图4和图6的结果,针对燃料组件(fuel)、内部格架(grid)、容器侧表面(wall1)、容器顶面(wall2)的温度,比较含太阳暴晒(Y)和不含太阳暴晒(N)工况下最高温度随外壁面发射率的变化规律,如图8所示。不同工况的计算结果都表明,外壁面发射率越高,容器各部位的温度越低,但影响程度不同。有太阳暴晒工况的发射率对容器各部位温度影响程度远低于无太阳暴晒工况。因此,通过增加外壁面发射率的方式,仅可有效降低无暴晒工况的容器各部位温度,但无法有效地降低有暴晒工况的容器各部位温度。
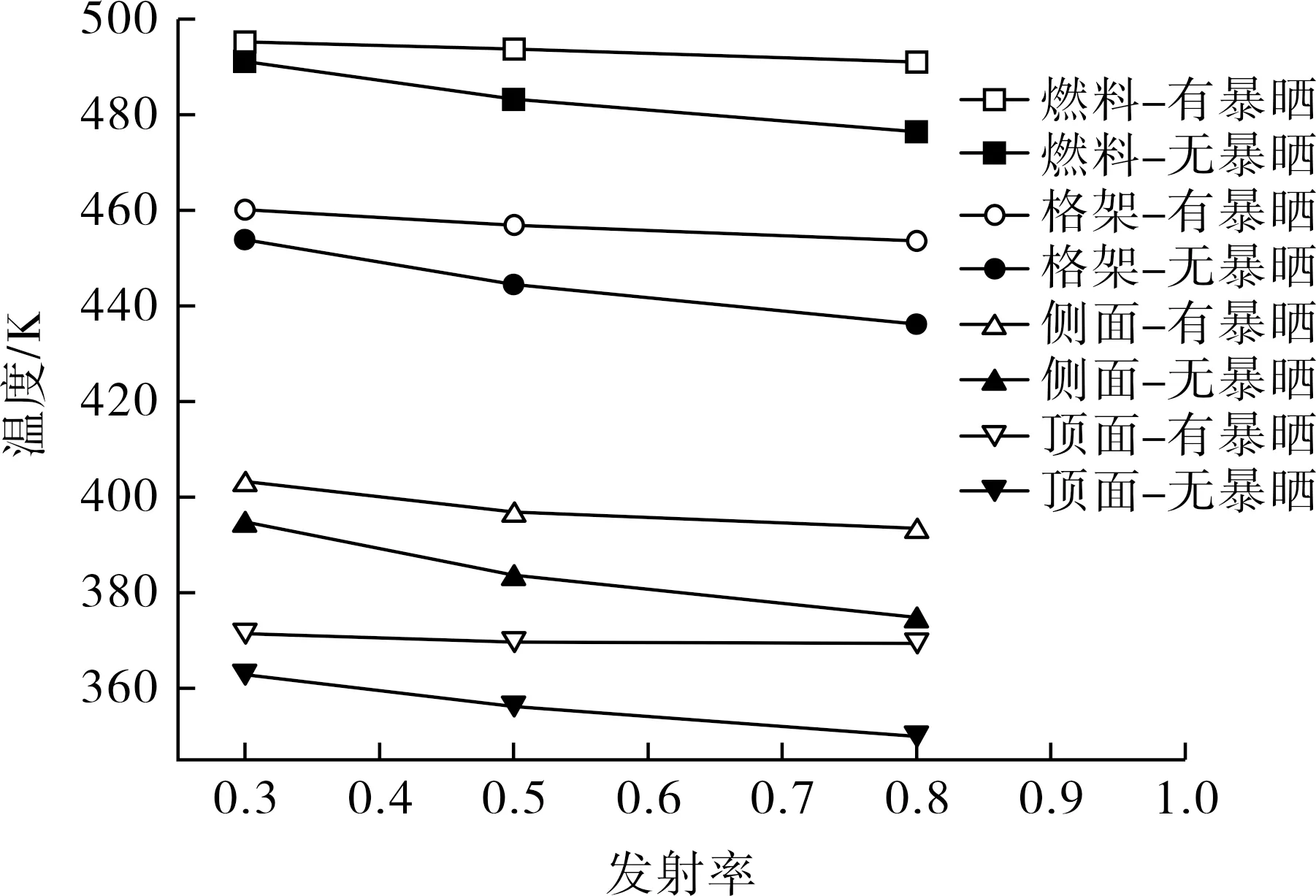
图8 不同工况下不同部件最高温度随外壁面发射率的变化曲线
表5列出了有暴晒下的传热功率。可以看出,当外壁面发射率增加时,总功率和总辐射功率明显增加,总对流功率变化不大。同时,当外壁面发射率从0.3增加至0.8时,总功率增加了1.25倍,而辐射功率增加了1.68倍。辐射功率增幅大于总功率增幅,说明了虽然外壁面发射率的增加可使太阳辐射能量增加,但同时也使辐射功率增加得更明显。
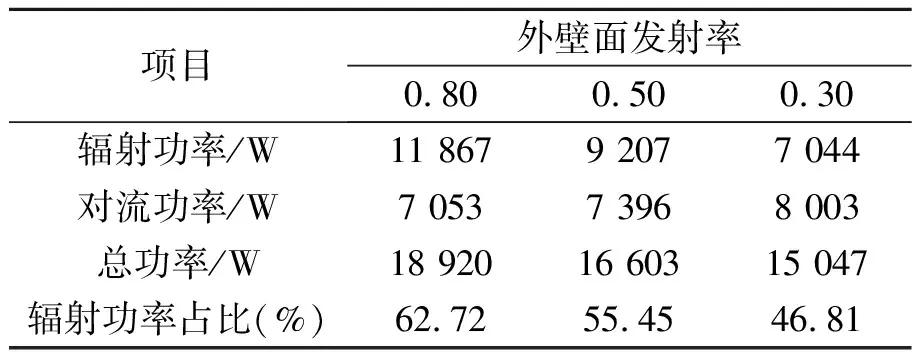
表5 有暴晒下不同外壁面发射率的传热功率及相对变化
3.2 容器内部壁面发射率对传热特性的影响
容器内部除固体间紧密贴合的壁面外,还存在接触氦气的固体壁面,需考虑其辐射传热。为论证内部壁面发射率对传热的影响,比较了有太阳暴晒工况下,内部壁面发射率设置为0.22,0.80,1.00时的温度分布,如图6(a)和图9所示。

(a)ε=0.80
容器内部壁面发射率从0.22增加至0.90,燃料包壳最高温度仅降低约2 ℃。由此可知,容器内部壁面发射率对容器各部位温度影响很小。其主要原因是,容器内部结构采用紧凑布置方式,固体壁面两侧基本为固体与固体接触,较少与氦气接触的固体壁面,辐射相比其他两种传热机理的功率占比很小。
为进一步论证容器内部其他两种传热机理的相对关系,通过设置氦气域为固体域,将原流体属性物性参数修改为固体属性下的物性参数,从而忽略了容器内部对流和辐射,实现容器内部仅考虑单一热传导的传热机制。
仅考虑热传导条件下容器内部传热效率提高,简化传热模型的整体温度较精确模型低3.5 ℃,如图10所示。说明容器内部传热以热传导方式传递了绝大部分热量,而对流和辐射传热方式占总功率比重较小。其原因在于,燃料篮内部的氦气被燃料格架分隔开,且局部位置温差驱动力小,不利于在容器内部形成稳定且高流速的自然循环流动,对流传热效果不佳。采用不考虑容器内部对流和辐射的方式,虽然对容器各部位温度影响不大,但该方式强化了内部传热,使得计算假设可能不够保守。
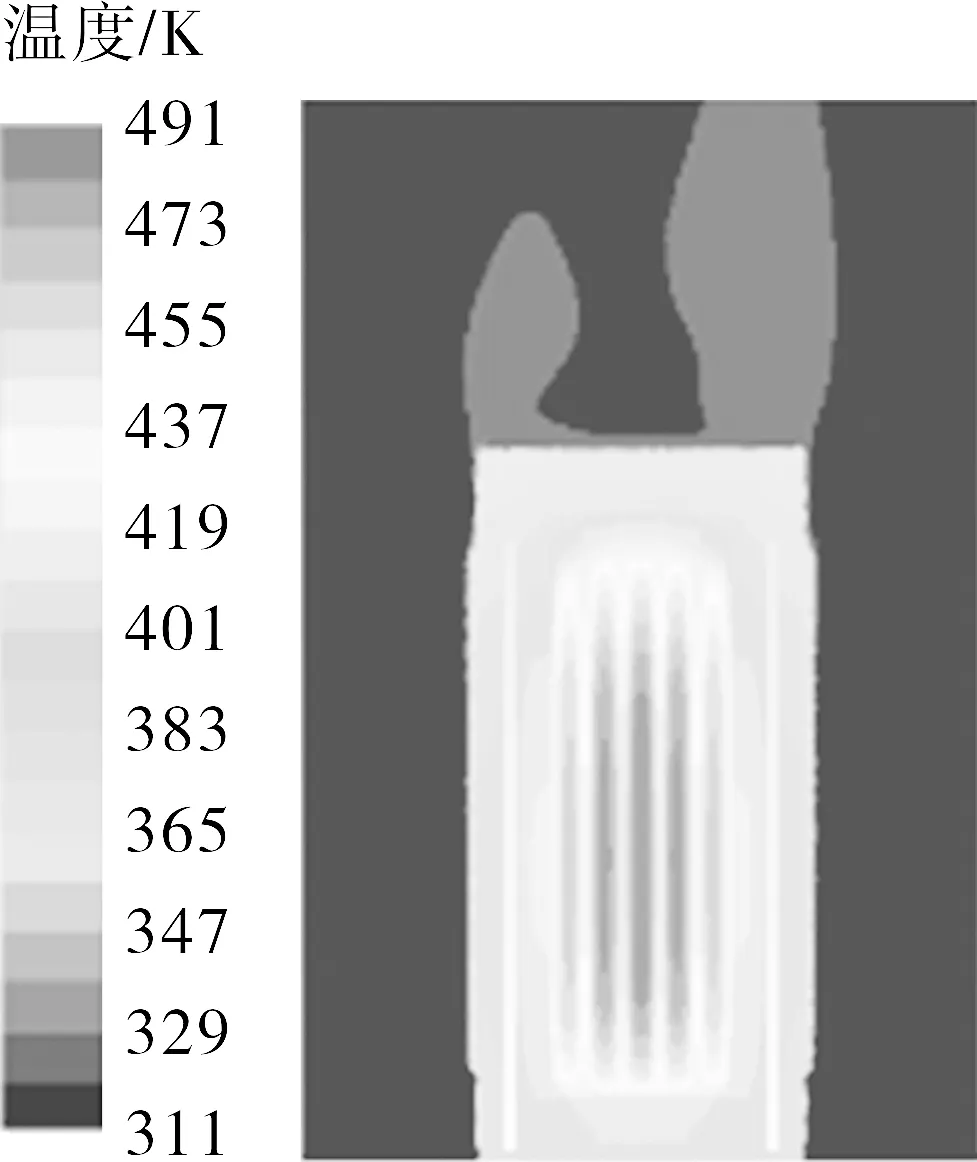
(a)考虑传导、对流和辐射
3.3 外部环境发射率对传热特性的影响
乏燃料容器采用集中存放形式贮存,辐射散热不可避免被外部环境反射,实际外部环境的发射率应小于1,分析计算中应予以考虑实际存放方式对外部环境发射率的影响。
为研究外部环境可能对容器辐射能量产生反射作用,设置了不同外部环境发射率(1.00,0.80,0.50),对比不同外部环境发射率下容器各部位温度分布,如图6(a)和图11所示。可以看出,当外部环境发射率越高,容器的整体温度越低。这归因于当外部环境发射率小于1,则有一部分容器辐射的能量受到外部环境的反射,容器往外辐射传热功率将会降低。
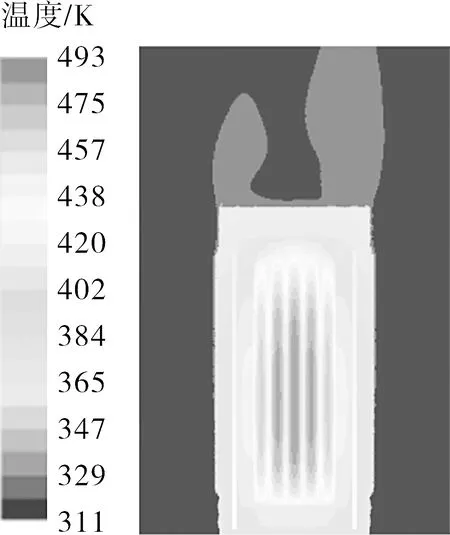
(a)ε=0.80
4 DO辐射模型验证
容器外部空间侧表面承受容器侧面和顶面的辐射传热,基于代数分析法和漫灰表面的辐射假设[12],计算含翅片结构容器外壁面对外部环境的辐射功率。通过对比CFD辐射功率和计算功率,验证DO模型CFD计算结果。对于含翅片的乏燃料贮运容器外壁面,首先基于代数分析法得到无翅片外壁面辐射功率,并假设翅片对表面积的增加倍数为η,可得带翅片外壁面的角系数和辐射功率。
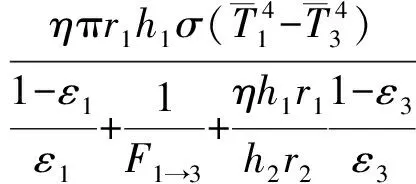
(3)
(4)
(5)
(6)
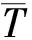
为验证DO辐射模型的适用性,以外部空气域侧面为对象,基于代数分析法和漫灰表面模型,根据式(2)计算翅片侧面以及顶面向空气域侧面辐射的传热功率。选取的工况载荷如表2所示。
将采用式(2)计算含翅片外壁面辐射功率与CFD结果进行对比(见表6),发现辐射功率随发射率的变化趋势基本一致,二者数值相差在10%以内。计算结果误差主要来源于公式法无法考虑壁面温度不均匀性,且简化采用了代数分析法推导有翅片结构的角系数,可能引入一定误差。
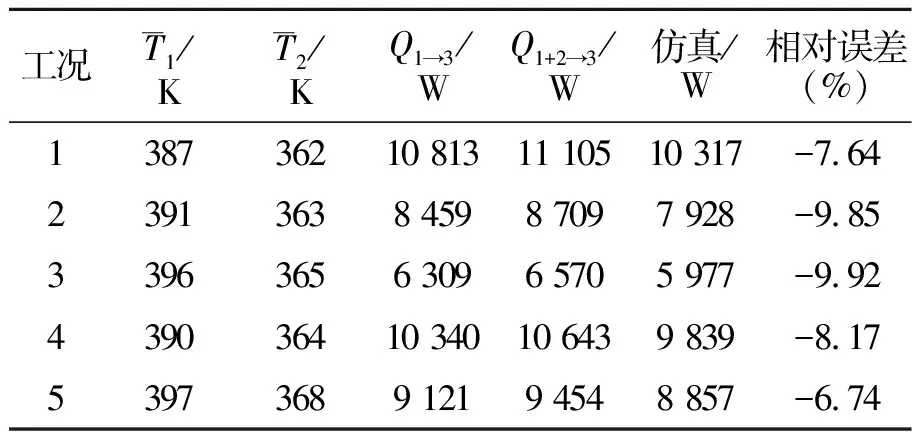
表6 不同工况下DO辐射模型验证结果
同时由表6可以看出,容器外壁面发射率越大,对外部环境的辐射功率越大;外部环境发射率越大,对外部环境的辐射功率也越大;容器侧面温度远高于容器顶面温度,表明容器侧面是辐射能量的主要来源。
5 结语
(1)容器外壁面发射率从0.30增加至0.80,无太阳暴晒工况的燃料包壳最高温度变化幅度是有太阳暴晒工况的3.51倍。容器内部壁面发射率从0.22增加至0.90,燃料包壳最高温度仅降低约2 ℃。容器外部环境的发射率对容器传热主导方式的影响明显。
(2)对于热传导占绝对主导的容器内部环境,建议优先选取热导率高的燃料篮结构,其他热参数如发射率、内部氦气压力等非关键参数影响较小。但需要注意避免中子屏蔽材料、容器外表面涂漆的温度超过功能失效温度限值。对于辐射和对流共同主导的容器外部环境,提高容器外表面的发射率和外部环境的发射率可有效降低容器的整体温度。
(3)结合代数分析法和漫灰表面模型对含翅片结构CFD辐射功率计算结果进行验证,公式计算结果和CFD计算结果吻合,误差小于10%。
该研究成果可在辐射传热方面对乏燃料贮运容器的热工分析及结构设计提供指导和借鉴。

