管内气液两相流动压降关联式研究进展
李 响,李秋英,密晓光,陈 杰,邱国栋,蔡伟华
(1.东北电力大学能源与动力工程学院,吉林 吉林 132012;2.中海石油气电集团有限责任公司,北京 100027.)
天然气作为优质清洁能源目前已经得到广泛应用[1],但是天然气在开采后面临运输和存储问题,故一般将天然气进行液化然后运输和存储.液化过程中,天然气主要以气液两相的形式在换热器内流动,由于气液两相之间存在复杂的质量、动量和能量传递,气液相界面易变形,气液分布不均匀、不稳定等特性导致准确计算其换热系数和摩擦压降难度较大.文献[2]综述了管内气液两相换热关联式研究现状,本文重点综述压降关联式研究进展.天然气属于非共沸混合工质,在冷凝时,气相和液相的组分不同,相变温度一直在不断变化.现有关联式并不是基于天然气提出,且不同关联式计算结果差异很大,适用范围有限,更加准确的关联式有待进一步研究.Dukler[3]基于单相流摩擦压降计算公式,提出了经典的均相流模型.该模型虽然计算简单,但模型过于粗糙,可靠性低.Lockhart-Martinelli[4]在水平管中对水-空气双组分两相流研究的基础上提出了著名的分相流动模型,同样因经验性过强,理论依据不足,故通用性不强.Neeraas[5]采用6种经典压降关联式(Lockhart[6],Fuchs[7],Chisholm[8],Friedel[9],Carter[10],Wallis[11])计算丙烷在1.2 MPa,质量流率为250 kg/(m2·s)下的摩擦压降,发现不同关联式结果仍然差异很大.
为此,本文从经验关联式以及理论关联式两方面出发,对目前已有的研究进行整理,为管内气液两相流摩擦压降的准确计算提供依据.
1 管内气液两相流摩擦压降经验关联式
1.1 均相流模型
两相摩擦压降最早使用的是均相流模型,均相流模型认为不同相间流体速度相同.此时,气液为均匀混合且相间无滑动.均相流的假设条件为:
(1)气相与液相速度相同;
(2)气相与液相满足热力学平衡状态方程;
(3)可使用单相流体的摩擦阻力计算公式来计算均相流的沿程摩擦阻力.
Dukler[3]法常用于均相流的摩擦压降计算,计算中各参数使用混合后的物性参数进行计算.具体计算公式如下:
(1)
(2)
(3)
ρf=βρg+(1-β)ρg
,
(4)
μm=βμg+(1-β)μl
,
(5)
公式中:Rem为气液混合物雷诺数;μg和μl分别为气相动力粘度和液相动力粘度,Pa·s;λm为气液混合物的摩擦系数;νm为气液混合物的速度,m/s.其中两相平均黏度的计算公式只是Dukler推荐的算法,学者们给出了不同的计算公式.其他均相流模型的具体表达公式如表1所示.

表1 均相模型
1.2 漂移流模型
漂移流模型又叫混合模型,该方法考虑气相与液相之间的滑脱影响,通过引入气相漂移速度这一参数来计算持液率,其他参数的计算方法与分相流(或均相流)计算方法相同.
假设各相速度不同,此时气液相间为有滑动特性的混合物.漂移流假设条件如下:
(1)气相与液相速度不相同;
(2)气相与液相满足热力学平衡状态方程;
(3)可使用单相流体的沿程摩擦阻力计算公式来计算漂移流的沿程摩擦阻力.
1.2.1 分相折算模型
分相折算系数法最经典的是Lockhart-Martinelli[6]法,该方法认为气相与液相之间无相互作用,把管道认为是气相与液相两条管道组合而成,通过气相与液相两条假设的管道压降得出真实管道内两相压降,并定义了Lockhart-Martinelli参数,该参数用X2来表示,具体计算公式如公式(6)所示.
(6)
Chisholm给出了φν、φl和X的函数表达式,如公式(7)、公式(8)所示.
(7)
(8)
Lockhart-Martinelli计算法是早期的混输计算方法.式中C为Chisholm系数、X为马丁内利参数.φν为气相折算系数,φl为液相折算系数.该公式适用范围有限,仅在小管径下计算效果较好,因此不同学者基于分相折算系数模型给出了不同管径与不同工质下的分相折算模型表达式,具体表达式如表2所示.

表2 分相折算模型
1.2.2 全相折算系数法
Chisholm[8]提出了一种经典的全液相折算系数计算方法:
(9)
(10)
(11)


表3 全相折算系数模型
1.2.3 两相增强因子法
Fuchs[7]法是经典的两相增强因子法.Fuchs法由挪威工业大学提出,计算结果和多个实验数据点吻合较好,得到一定的认可.该方法是在水平管R12蒸发实验得到的,测试管径为20.4 mm,压力为1.2 bar~2.6 bar,质量流率为65 kg/(m2·s)~775 kg/(m2·s),质量含气率为0~1.
该方法的基本思想是使用了一个两相增强因子将气液两相的压降关联起来:
(12)
公式中: (dP/dL)x=0和(dP/dL)x=1分别表示相同质量流量下饱和液相和饱和气相的摩擦压降,按单相流动的摩擦压降计算,一般应用时,两相修正系数是下列参数的函数:
(13)
Fr数计算如下:
(14)
当Fr数大于1.45,或者Fr数大于0.65且含气率大于0.15时,Ψ只是含气率的函数,这个情况下,流型预计是环状流,Ψ的函数形式由实验确定.Neeraas[5]通过实验验证发现该关联式在某些情况下误差增加,提出了如下修正:
(15)
修正之后的模型与Neeraas[5]实验数据吻合很好.该模型从原理上看,比分相折算和全相折算系数法要好.
1.2.4 基于流型的计算模型
上述压降关联式都没有区分流型,计算方便,由于不同的流型流动规律不同,故区分流型给出的关联式更加符合流体力学原理.大量研究发现,两相摩擦压降折算系数φ随马丁内利数Xtt的函数在某些情况下是不光滑的,斜率存在不连续的问题,分析认为这是由于流型的影响造成的[24].Baker[25]根据自己实验数据绘制的流型图,分别给出了泡状流、塞状流、分层流、弹状流和环状流摩擦压降的分气相折算系数计算公式.其计算公式为
(16)
针对不同流型,分气相折算系数φν具有不同取值.其中:
气泡流:
(17)
气团流(塞状流):
(18)
分层流:
(19)
冲击流(弹状流):
(20)
环状流(注:当d>0.25 m时取d=0.25 m)
(21)
公式中:A为流通面积,m2.
另外,波浪流压降计算应该采用汉廷顿(Huntington)公式:
(22)
(23)
公式中:f为管壁摩擦系数;Vsg为气相折算速度,m/s;Gl为液相的质量流率,kg/(m2·s) .
Baker[26]指出流型图上的转换界限虽然画的是一条线,但实际上的过渡区是一个很宽的范围,在流型转换界线附近按不同的流型选择关联式,会得到高达5倍差异的计算结果.
2 管内气液两相流摩擦压降理论关联式
2.1 分层流等效粗糙界面模型
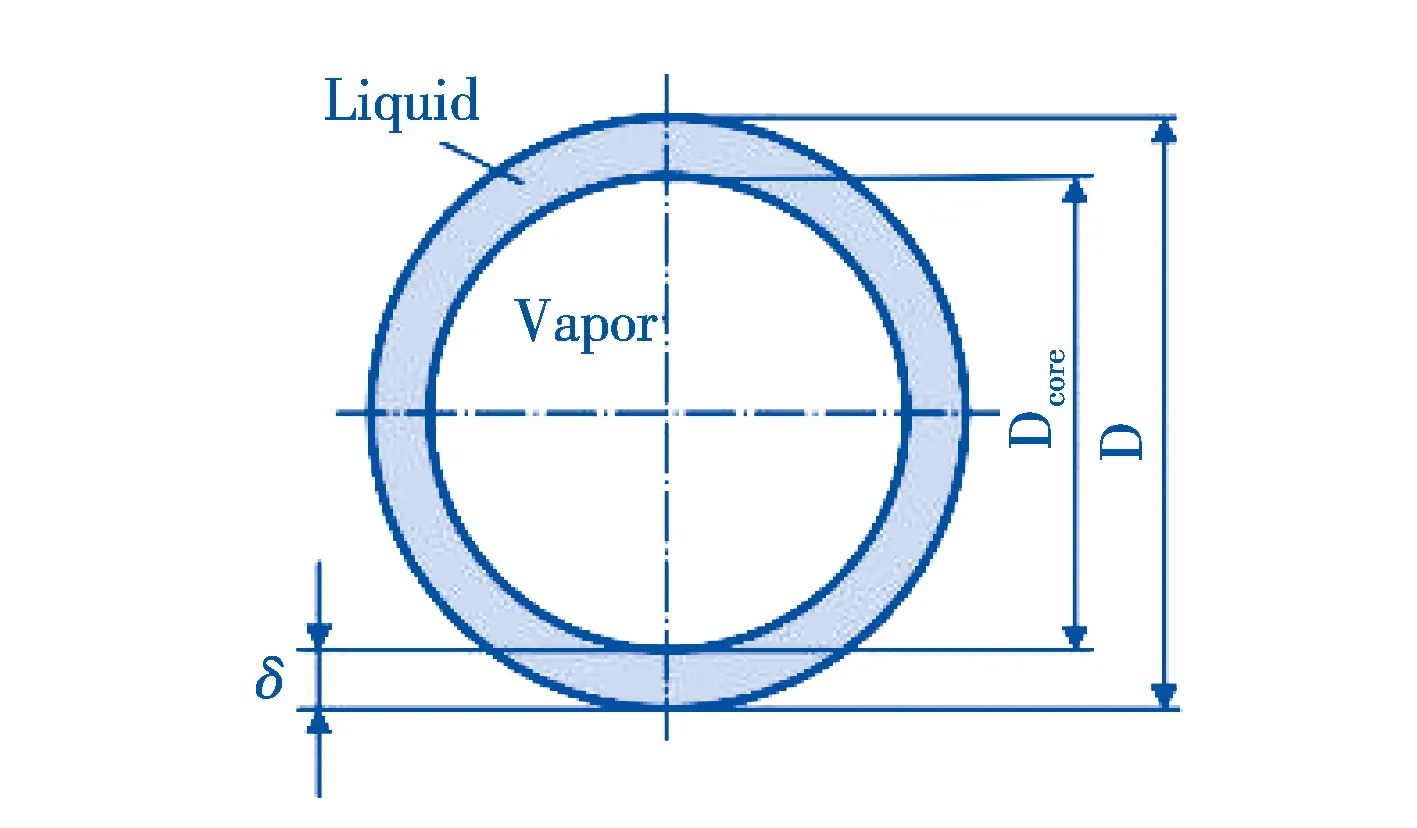
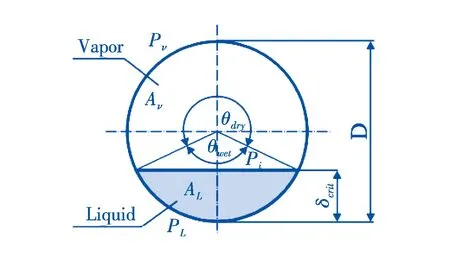
Hart等[27]研究表明,当气相流动速度较高时,此时两相界面不是平坦的.通过对低持液率下分层流界面研究,给出了等效粗糙界面模型.得到了低含液率下水平管道气液流动过程中含液率和压降的计算方法(0 (1)持液率HL的计算公式为 (24) (2)壁面润湿角θ的计算公式为 (25) (3)两相压降ΔPTP的计算公式为 (26) 如果νg≥νl并且0 (27) 公式中:νg、νl分别为气相和液相速度,m/s;fTP为两相摩擦系数. 在管道中流动的气、液相界面并不是平坦的,通过轴向观察可以得出,当气相速度逐渐升高时,管道中气相和液相界面会呈现下凹的变化.气相速度越大,下凹越明显.导致理论预测的几何关系与实际结果有明显偏差.如采用水平界面模型和等效粗糙表面模型进行计算时,会导致持液率和压力梯度偏差较大,而基于双圆环理论与重心前移思想提出的双圆环模型[28]可有效减小偏差.该模型由内管壁圆环和假想的偏心圆环组成.如图1所示. 图1 双圆环模型图 (1)“双圆环”模型中界面摩擦系数的相关性公式: (28) 公式中:Θ为壁面润湿分数;HL为持液率;νsg为气体折算速度,m/s;νsg.t为气体临界折算速度,m/s. (2)气壁摩擦系数fg的计算公式为 (29) 公式中:Ug为气相的实际速度,m/s;Dg为水力直径,m;νg为气相的运动粘度,m2/s. νg=μg/ρg . (30) (3)壁面润湿分数的计算公式为 (31) 公式中:Fr是Froude数. (4)转换边界的实际气体流速的计算公式为 (32) 公式中:νl为液相的运动粘度,m2/s;νl=μl/ρl;s为系数. Thome等[29]基于几种简化的界面两相流动结构,采用现象学方法建立了沸腾管内新的两相摩擦压降模型.如果流态是已知的,可以简化界面结构,提出一组方程来确定两相压降,同时要避免在流型过渡区出现数值跳跃. (1)环状流 简化环状流示意图如图2所示.忽略夹带作用,假设液膜在圆周上具有均匀的厚度δ. 图2 简化环状流示意图 基于稳态气液相动量平衡方程,可以得到摩擦压降表达式: (33) 公式中:δ为液膜厚度,m;τi为界面剪切应力,N. 环状流界面摩擦系数fi的计算公式为 (34) 公式中:We为Weber数;fi为界面摩擦系数;μg和μl为气相和液相的动力粘度,Pa·s;σ为表面张力系数,N/m. 此时摩擦压降可按下式计算: (35) (2)弹状流和间歇流 根据其流型图,弹状流和间歇流位于纯液相和环状流之间,是一种不稳定的流型,难以像环状流那样直接建模计算,因此将该流型衔接的两种流型(纯液相和环状流)进行加权得到弹状流和间歇流的的摩擦压降: (36) 公式中:ΔPl0为单相摩擦液压降,Pa;εIA为间歇流到环状流过渡边界处的截面含汽率. (3)分层波状流 分层波状流的简化示意图如图3所示. 图3 分层-波状流示意图 在这种情况下,干涸角θdry按下式计算: (37) 两相摩擦压降表达式为 (38) (4)分层流 如果x≥xIA,那么: (39) (40) 如果x (41) 公式中:ΔPl0为单相摩擦液压降,Pa;εIA为从环状流到间歇流过渡的截面含汽率;θstrat为起始角. 该文献作者认为上述建立的模型具有如下特点: (1)遵循压力梯度随蒸汽质量的变化规律. (2)能在高蒸汽质量下捕捉更大的压力梯度. (3)包括了界面波的影响. (4)考虑了流型的影响. (5)采用实际平均速度,而不是折算速度. 综上,由于两相流压降的复杂性,目前经验关联式仍然占主导,理论关联式相对较少.无论是经验关联式还是理论关联式,不同学者都做出了假设.目前管内气液两相流压降关联式特点总结如下: (1)国内外学者虽然做了大量的研究,得到了许多不同的计算关联式,但是这些关联式基本都是在单相摩擦压降基础上乘以两相折算系数或两相增强因子得到,折算系数或增强因子关联式基本都是从研究者自己或他人的试验数据基础上总结得来的经验关联式,经验性较强,通用性难以保证. (2)现有的理论关联式也仅仅是在大量简化假设条件下采用了理论的架构,其中的关键参数仍然离不开经验拟合,从计算精度上看,对于特定的工况现有理论关联式并不具有明显的优势. (3)两相流因其复杂性,已有文献普遍把±30%作为关联式与实验值之间可接受的偏差.因此现有关联式难以满足各种工程设计计算的精度和可靠性要求.更可靠的关联式还有待进一步探索. 实验是理论的先行,文献中烃类工质以及超临界工况实验数据较少,不同数据源之间也存在偏差,在今后的研究中应加强实验数据的准确性.由于两相流的复杂性,流型研究是两相流的关键,基于流型的压降预测方法准确度较高,是未来管内气液两相流压降预测的发展方向.2.2 分层流双圆环模型
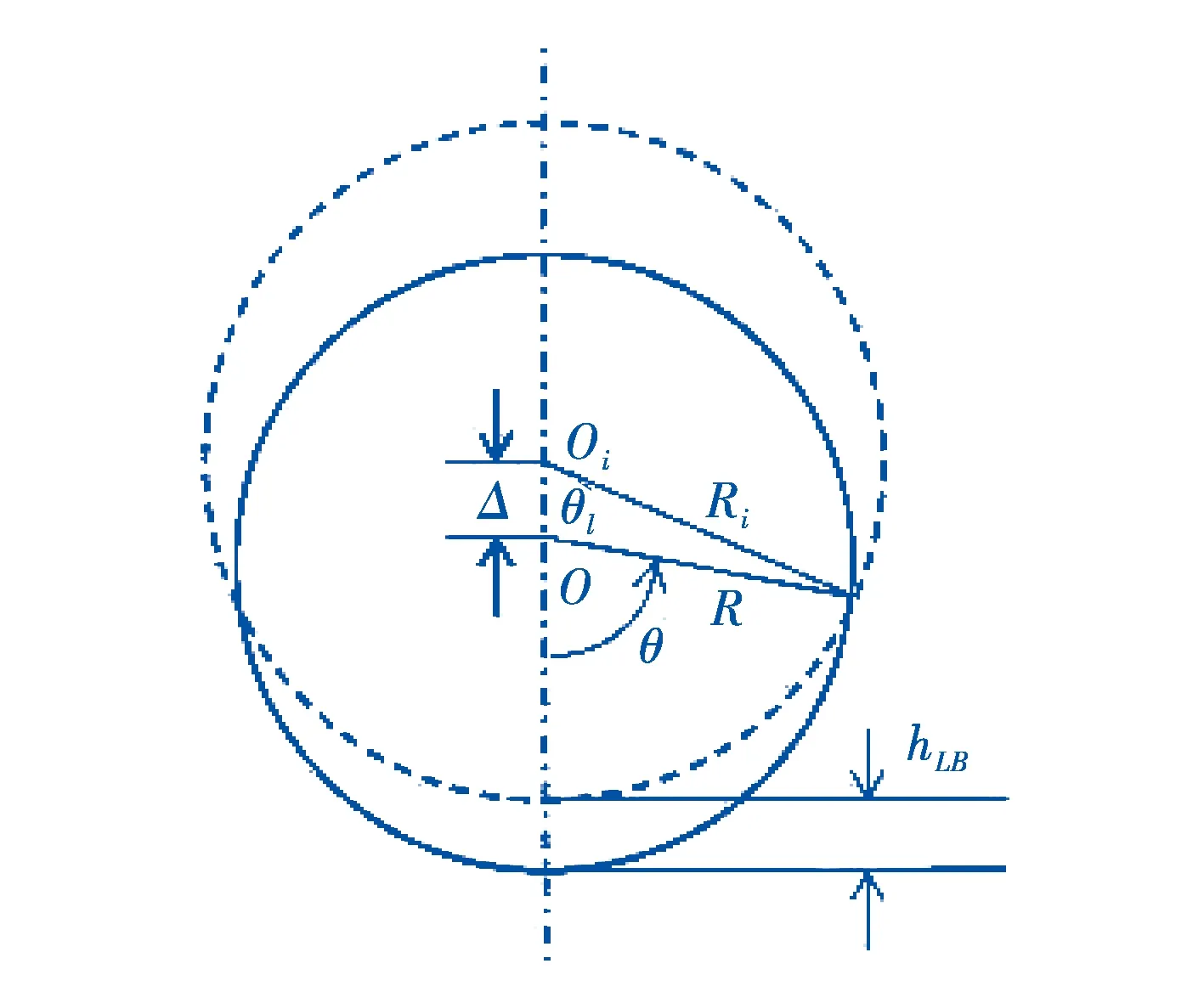
2.3 多种流型Thome法
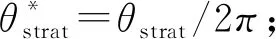
3 结 论

