基于MEEMD-Prony联合算法的电力系统低频振荡模态辨识

雷志勇，江 灏，李中胜

(1.福建水利电力职业技术学院电力工程学院，福建 永安 366000；2.福州大学电气工程与自动化学院，福建 福州 350108；3.福建水利电力职业技术学院，福建 永安 366000)

电力系统中并列运行的系统或发电厂失去同步，系统中将会出现功率、电压等电量不同程度振荡的现象，称为电力系统低频振荡.低频振荡是电力系统中最为严重的一类系统事故，持续时间长，可能引起电网大停电，影响电网的安全稳定运行[1].随着我国建设特高压骨干输电网络步伐的加快和总输电容量的不断增加，电力系统低频振荡现象时有发生.为确保电网安全稳定运行，低频振荡问题亟待解决.研究电力系统低频振荡，关键在于找出导致起振的原因及影响因素，采取有效的控制措施，进而抑制低频振荡发生，可采用信号模态辨识方法达到此目的[2].

当前，电力系统低频振荡的模态辨识中，常用的方法是Prony算法，经Prony算法分析后的数据准确、稳定性良好.刘鹏翔等[3]采用Prony算法针对含风电区域电网低频振荡模态及影响因素开展研究；Wadduwage[4]用多Prony模型识别了衰荡振荡中的主导低频模式.但Prony算法容易受噪音影响，在信噪比大于40dB的情况下，单纯地使用该算法求解容易出现严重误差，故需要通过滤除噪声再对数据进行处理[5].经验模态分解(Empirical Mode Decomposition，EMD)和集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)常用来进行信号中的噪声滤除，众多学者采用此类方法取得了一定的效果.例如，Li等[6]分析了EMD方法的滤波特性并用于信号滤波；罗小元等[7]将EMD方法用于工业无线通信滤波中；蒋沅等[8]将EEMD应用于超声水表的信号处理；Li等[9]将EEMD用于轴承故障信号特征提取.但经过应用验证，发现这两种方法存在模态混叠等问题亟待解决[10].采用改进的集合经验模态分解(Modified Ensemble Empirical Mode Eecomposition，MEEMD)算法分解重构后的信号与原信号非常相似，基本可以滤除干扰的噪声信号，而且有效的改善了EMD和EEMD方法的模态混叠问题[11].

据此，本文提出了一种MEEMD-Prony联合算法，针对仿真算例和实际电力系统信号应用该方法进行了低频振荡模态辨识.实验结果证明，该方法抗噪性能好，辨识结果精确，对研究电力系统低频振荡的成因，保障系统的安全运行有非常重要的作用.

1 基于MEEMD的Prony算法

1.1 改进的集合经验模态分解(MEEMD)

鉴于EMD方法和EEMD方法可能产生模态混叠和模态分裂，学者们采用了能够抑制模态混叠现象、解决模态分裂问题并提高运算效率的改进的EEMD算法，即改进的集合经验模态分解方法[14].该方法在非平稳信号中加入均值为0的白噪声，并进行EEMD分解，将分解结果平均，再做EMD分解，即得到本征模态函数(Intrinsic Mode Function，IMF)和剩余分量.具体过程如下.

首先向不平稳信号x(t)中加入均值为0的白噪声信号(即±ni(t))得：

(1)

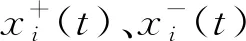
(2)

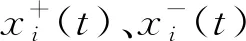
(3)

因ci(t)存在模态混叠且不一定是标准IMF分量，故将ci(t)定义为预本征模态函数(Pro-IMF)，对其再进行EMD分解，得到：

(4)

(5)

最终得到MEEMD分解的表达式如下：

(6)

1.2 Prony算法

Prony算法是提取平稳振荡模式的常用算法[15]，它针对等间距采样点，采用一组含p个具有任意相位、频率、幅值与衰减因子的指数函数的数学模型，输入信号(x(0)，x(1)，…，x(N-1))为主导振荡模式的IMF，其估计值的离散时间的函数形式为

(7)

公式中：Aki为第k个轨迹的幅值；θki为第k个轨迹的初相；fi为频率；σi为衰减因子；p为拟合的指数函数的个数；N为采样个数；Δt为采样时间间隔.

Prony方法的主要缺点是数据拟合的最终结果容易受到噪声影响，特别是当信噪比<40 dB时，其分析结果误差较大，这一缺点在实际数据处理前，对处理的数据进行滤波去除噪声即可解决.Prony方法的另一缺点则是无法反映动态过程的非平稳性，且无好的解决措施[16].

1.3 基于MEEMD的Prony算法的步骤

基于MEEMD的Prony算法的振荡模态辨识，流程步骤如下图1所示.

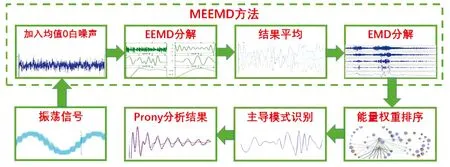
图1 MEEMD-Prony算法的振荡模态辨识流程图

对振荡信号进行MEEMD分解，获取其IMF分量并对其重构，将重构结果用Prony算法拟合，最终得到所需的结果.

2 数学算例分析

2.1 构造理想信号

为验证MEEMD-Prony联合算法的有效性，构造一低频振荡信号x(t)如下：

(15)

向信号x(t)加入噪声，得到纯净信号与加入噪声后的信号如下图2(a)所示.该信号由两组调幅信号组成，其中，纯净信号幅值为5，阻尼系数-0.5，频率为1 Hz；噪声信号幅值为2，阻尼系数-0.1，频率为0.5 Hz.经EMD分解产生6个IMF分量，而经MEEMD产生的IMF分量只有4个，如2(b)所示.将两种方法所得IMF分量重构，重构后信号如下图2(c)所示.

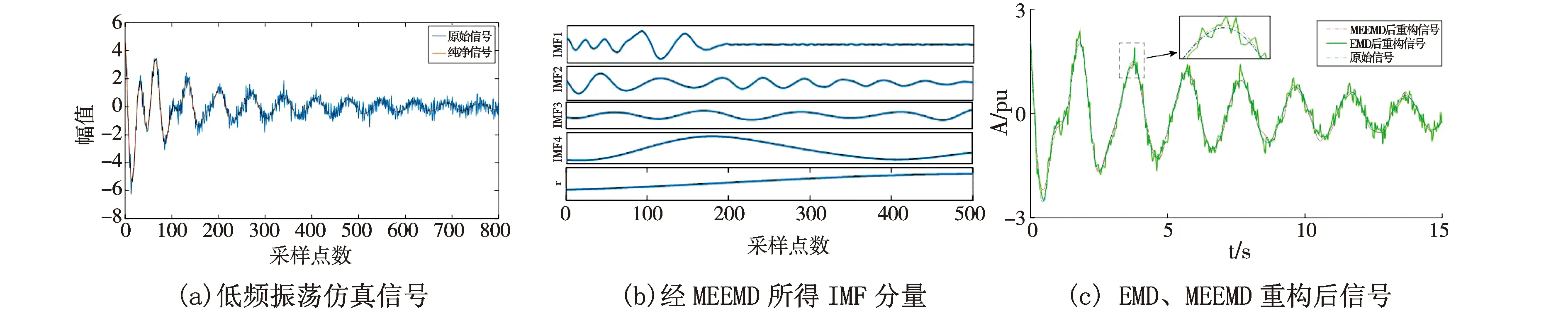
图2 算例信号构建

表1显示了重构后信号指标.结合图2、表1可以看出，EMD和MEEMD重构后信号与原始信号基本相符，但EMD重构出的信号仍然有毛刺存在.相比EMD，MEEMD分解产生的IMF分量更少，提升的信噪比更高，与原始信号的相关系数更高，均方误差更小分解重构后所得信号质量更好.

表1 重构信号指标

2.2 拟合结果及其分析

将低频信号x(t)用Prony算法、EMD-Prony算法、MEEMD-Prony算法进行拟合，辨识结果如下图3、图4、图5、表2所示.

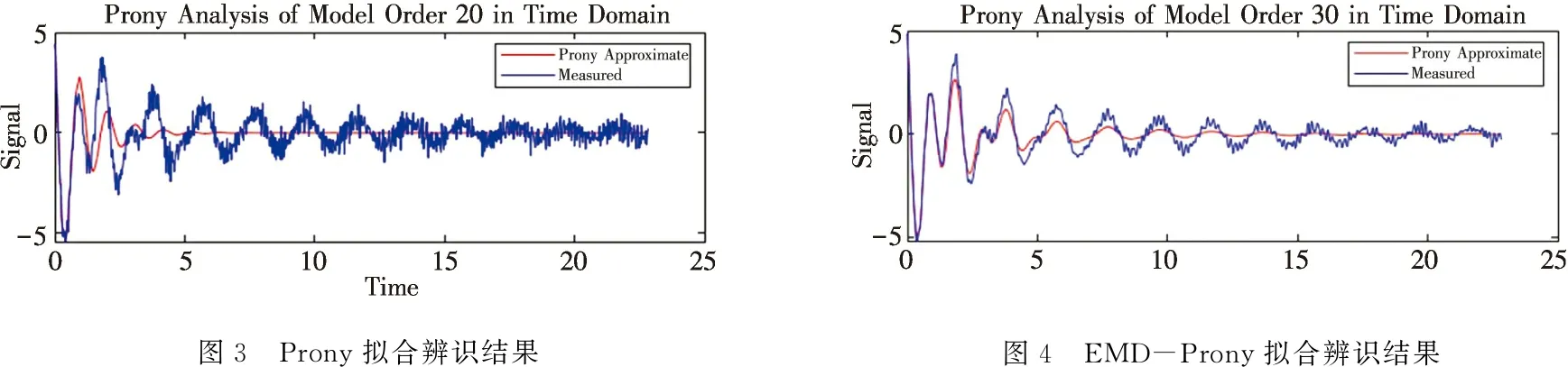
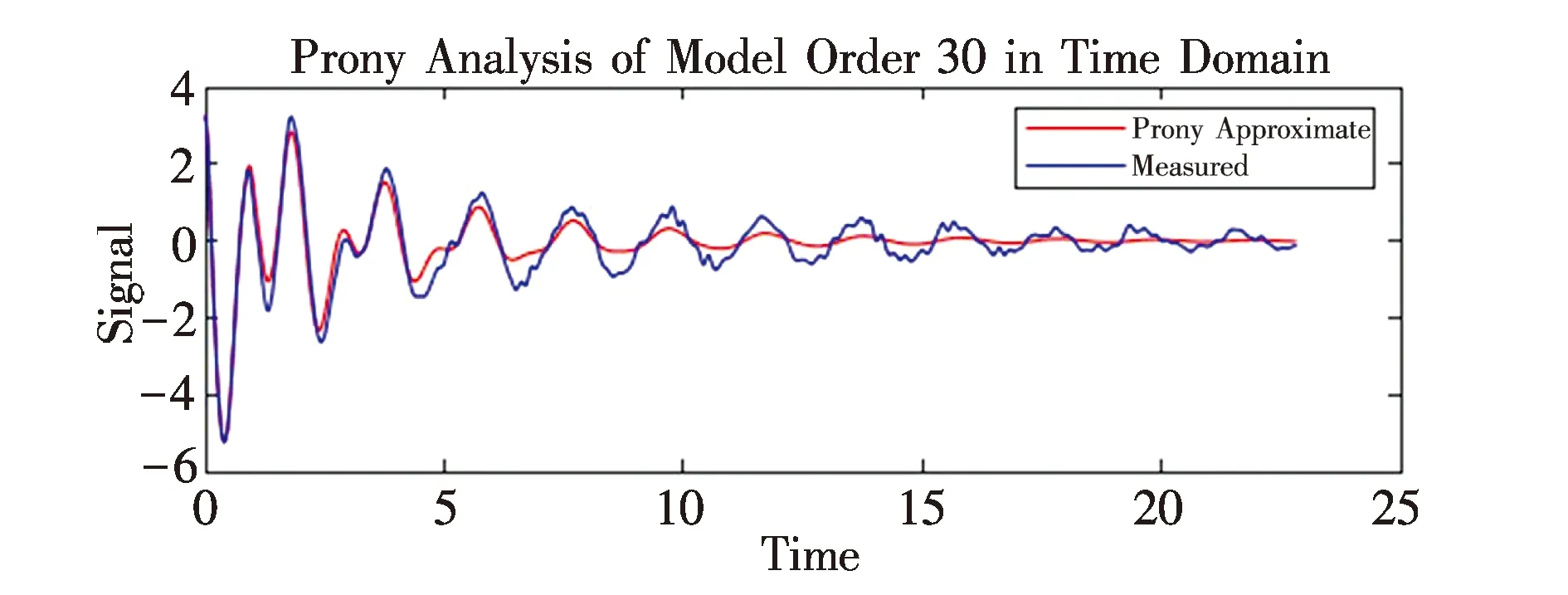
图5 MEEMD-Prony拟合辨识结果

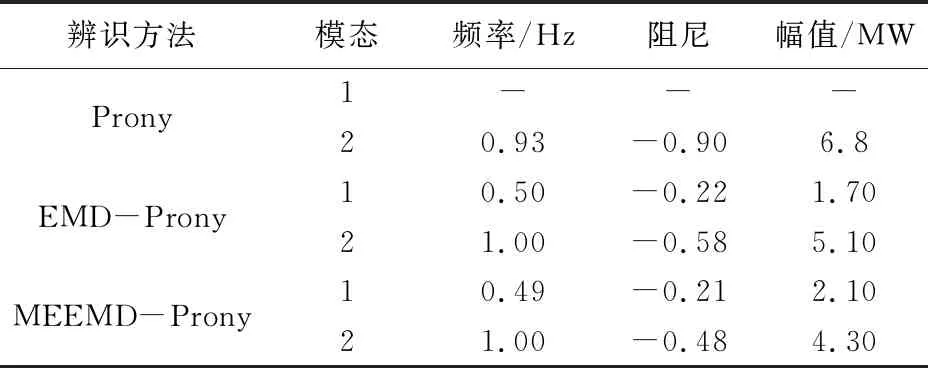
表2 辨识结果

由图3拟合结果可以轻易看出，由于受噪声影响，Prony算法的拟合结果与扰动前信号几乎完全不符.且由辨识结果表2来看，模态1丢失，模态2的数据振幅误差为1.8，频率误差为0.03，阻尼误差为0.4.辨识结果整体误差很大.由此可以看出Prony算法的拟合结果对噪声十分敏感，在处理含噪声干扰的信号时，无法得到准确的结果.

由图4拟合结果可以看到，经EMD滤波后的信号噪声减少，且Prony拟合结果与未加入噪声的纯净信号基本相符.由以上辨识结果可看出，模态1频率无误差，阻尼差距为0.12，幅值差距为0.3；模态2频率无误差，阻尼差距是0.08，幅值差距0.1，拟合结果无信号丢失且基本符合原信号.对比直接用Prony算法拟合的结果可知，EMD能够有效地滤除噪声，且经EMD滤波后的Prony拟合结果误差不会太大.

由图5拟合结果可以看出，经MEEMD滤波后的信号噪声相比EMD少很多，而且基本趋于稳定.信号的辨识结果，模态1频率无误差，阻尼的误差为0.11，幅值的误差为0.1；模态2频率误差0.1，阻尼的误差为0.02，幅值误差为0.7，相比经EMD滤波后的Prony拟合结果误差基本不大.且相比于EMD，可以看出MEEMD过滤后的信号更加稳定，噪声也基本滤除.

3 MEEMD-Prony算法于电力系统分析

3.1 EPRI-36节点系统

EPRI-36节点系统如图6(a)所示，考虑如下扰动：在1 s时BUS20至BUS22之间联络线20%处发生持续时间为0.1 s的三相短路故障，在1.1 s时故障消除，步长为0.01 s，仿真时长设定20 s.采集发电机G3相对功角信号(以G1为参考发电机)作为分析振荡信号，并在该信号中人工添加信噪比为9.5 dB的高斯白噪声得到的含噪振荡信号如图6(b)所示.

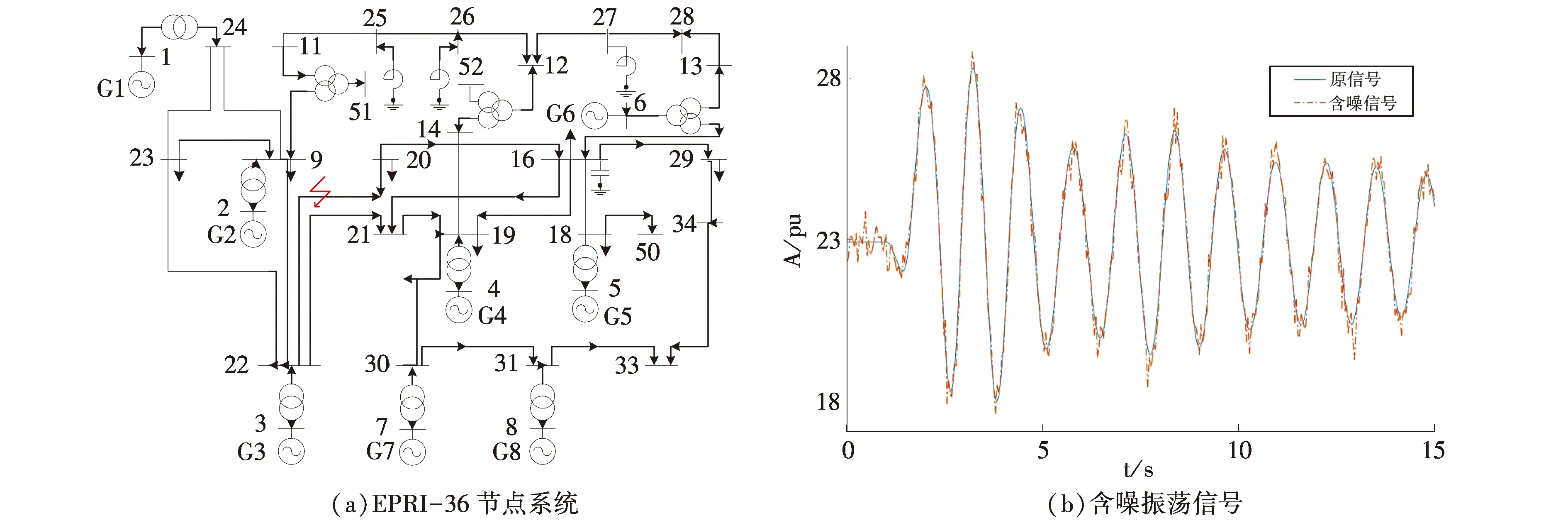
图6 EPRI-36节点系统及振荡信号

图6(b)所示低频振荡信号经EMD和MEEMD分解后所得IMF分量如下图7所示.

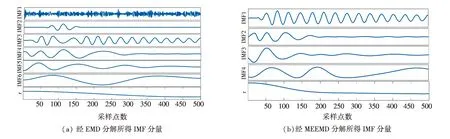
图7 EMD和MEEMD分解IMF分量

由图7可以看出，经EMD分解产生了6个IMF分量，而经MEEMD产生的IMF分量只有4个.将两种方法所得的IMF分量重构，重构后的信号如图8所示，信号的指标如表3所示.

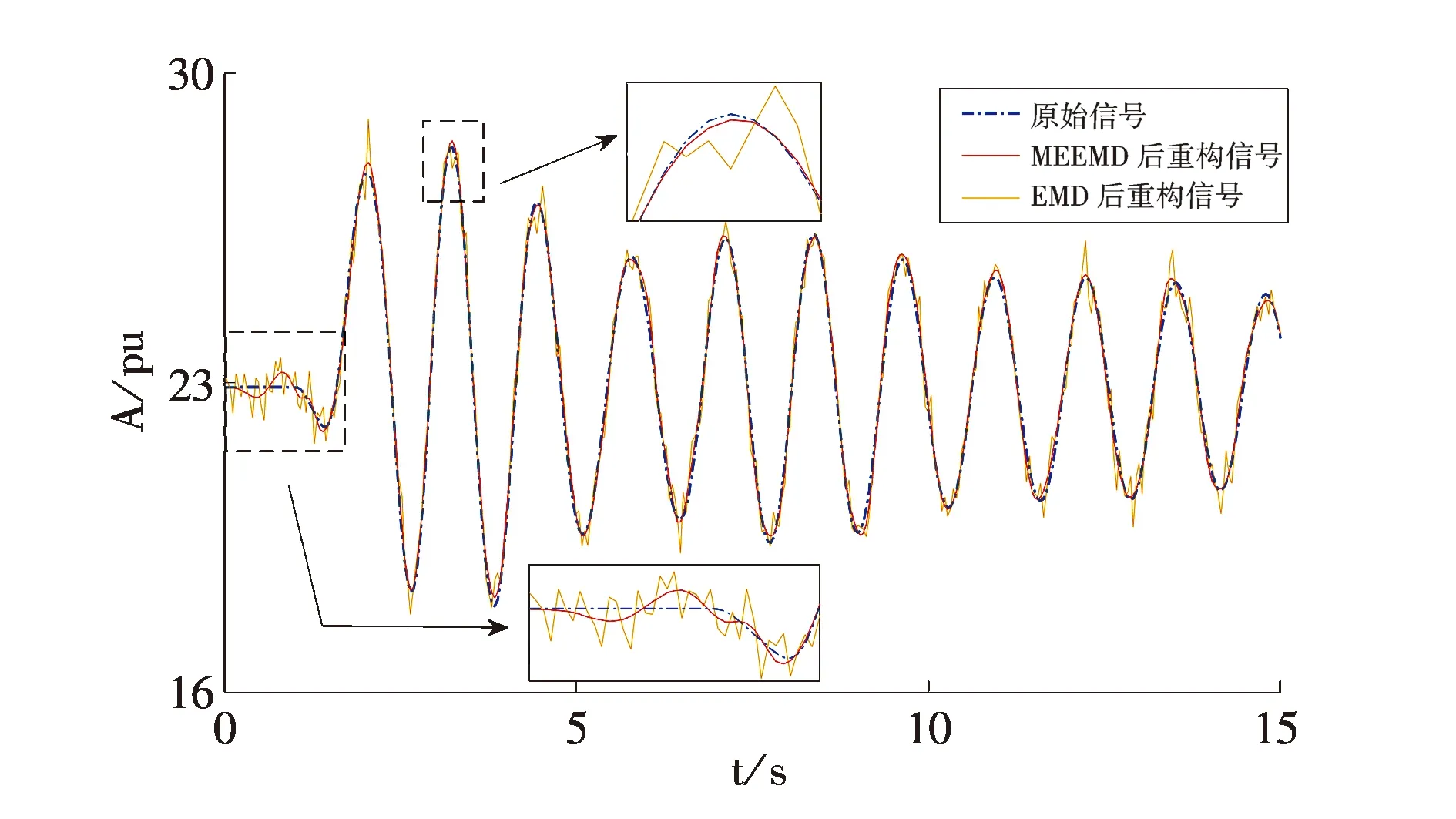
图8 EMD、MEEMD重构后信号

表3 重构信号指标

3.2 拟合结果分析

经过电科院PSASP软件对于本次故障小干扰特征值计算得知，在此方式下有2个弱阻尼主导振荡模态，一个频率为0.777 5 Hz，另一个频率为0.980 2 Hz.分别采用Prony、EMD-Prony和本文方法对含噪功角振荡信号进行模态辨识，并在表4给出结果.由表4中参数对比可知，在噪声干扰下，Prony算法只能辨识出其中一种模态频率；EMD-Prony算法虽能较完整地提取参数特征，但在精度方面上稍有不足；MEEMD-Prony算法能辨识出两种频率，且与小干扰稳定计算结果基本吻合.

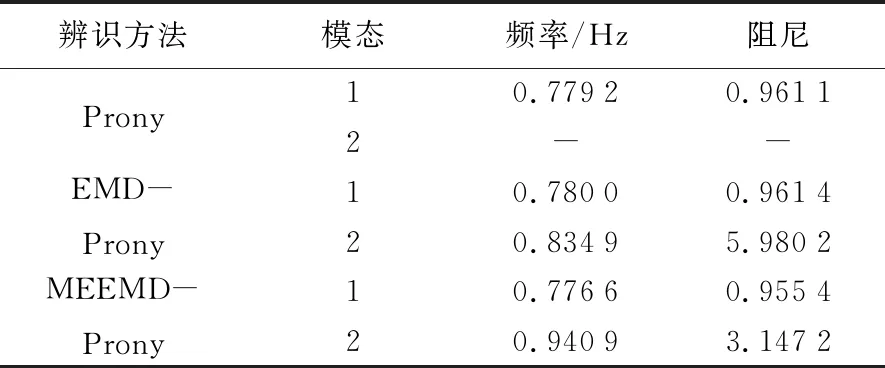
表4 辨识结果

4 结 论

该文首先介绍了电力系统低频振荡的模态辨识的常用方法及优缺点；其次详细介绍了基于MEEMD的Prony算法步骤及计算过程；最后通过仿真检验了MEEMD-Prony联合算法的有效性.综上所述可知，改进的集合经验模态分解(MEEMD)在数据的预处理上相比集合经验模态分解(EMD)要优秀很多，其对噪声的滤除更加彻底，所得数据也更平稳一些.Prony算法在经过滤波后基本可以得到精确度较高的模态数据.由以上结论可知，基于MEEMD的Prony算法对低频振荡信号的参数辨识非常有效，且拥有非常优秀的抗噪能力，对研究电力系统低频振荡的原因及其影响因素，保障系统的安全运行有非常重要的作用.