基于负荷模式能量的永磁风机电网功率振荡特性分析

刘 铖，王 旭，张宇驰

(东北电力大学现代电力系统仿真控制与绿色电能新技术教育部重点实验室，吉林 吉林 132012)

为实现碳达峰、碳中和的战略目标，找寻并应用能代替传统化石能源发电的新能源已经成为亟待解决的问题[1].可再生能源以其清洁、高效、低碳等优点发展迅速，其中以风力发电为代表的可再生能源将成为新型电力系统的重要组成部分.高比例风电并网电力系统是以新能源为主体，并由输电线路及负荷等部分组成的统一系统，以风电为代表的新能源发电设备接入系统导致系统惯量降低，加之风电自身的波动性、不确定性以及随机性导致了系统的低频振荡分析愈加复杂，系统的小干扰稳定特性发生变化，电力系统安全稳定运行面临着更大的挑战[2-6].传统大多是以源侧、网侧为切入点分析风电并网电力系统低频振荡特性，然而负荷作为系统重要组成部分，实时参与系统振荡过程，从负荷侧同样可分析系统的低频振荡特性，为电力系统小干扰稳定分析提供了新的角度，因此从负荷侧分析高比例风电并网电力系统小干扰稳定性具有重要的意义.

随着PMSG在电力系统中大规模推广和使用，国内外学者对于直驱永磁风机并网小干扰稳定问题展开了深入的研究.文献[7]建立了详细了16阶永磁风机小干扰模型，利用特征值分析法将该模型降为四阶，所得到的四阶模型通过时域仿真得到了和详细模型一致的结论.文献[8]研究了不同类型风电机组对系统小干扰稳定影响，证明了双馈变速风电机组(Double Fed Induction Generator，DFIG)在近距离、低渗透率情况对小干扰稳定性影响最有利.文献[9]对不同类型风机的振荡模式阻尼特性进行分析，并根据风机并网后系统动态特性因素的风电机组选型提出建议.文献[10-11]采用特征值分析法证明了直驱永磁风机出力增加对与风电强相关的振荡模式阻尼比呈现减少趋势，系统小干扰不稳定程度增加.文献[12]研究不同类型风电机组对系统小干扰影响与暂态稳定影响进行比较分析，证明不同类型的风电机组并网影响程度均不同.文献[13]研究了虚拟惯量控制下，PMSG对系统小干扰稳定性的影响主要体现在接入位置及容量有关.文献[14]分析了永磁风机运行参数对系统小干扰稳定性的影响.文献[15]分析了永磁风机机侧动态特性和网侧动态特性对系统机电振荡特性的影响.

由上述文献可知，目前分析PMSG并网对系统小干扰稳定性影响主要基于特征值分析法从源侧以及网侧进行研究.而特征值分析法是根据电力系统特征值进行求解，对于直驱永磁风机接入后系统振荡的物理过程描述尚不足.此外，现有研究内容大多分析直驱永磁风机对系统振荡模式阻尼比的影响，对从负荷角度分析风机接入对系统小干扰稳定影响鲜有研究，然而通过负荷侧也能表征出系统振荡特性，揭示风机参与振荡的具体过程，对负荷侧研究PMSG并网对系统小干扰稳定的影响也可为后续需求侧负荷调控提供理论依据.

针对以上不足，若可将能量函数与小干扰模式概念相结合，从负荷模式能量的角度展开对直驱永磁风机并网振荡参与过程进行研究，推出基于负荷模式能量系统小干扰稳定评价指标，实现对系统小干扰稳定性进行评价.在Power System Analysis Toolbox (PSAT)中构建含PMSG接入的四机两区系统进行验证，揭示含PMSG并网系统的低频振荡特性.

1 PMSG数学模型

永磁风机是一种基于全功率变流器的典型变速恒频风机，其模型如图1所示.永磁风机依靠背靠背的双脉冲变换器实现最优转速的控制，同时利用其自身网侧的变流器对有功功率和无功功率进行解耦以实现与电网的同步运行.永磁风机的优点体现在(1)永磁风机设备简单，减少系统运行损耗与机械故障的发生频率；(2)由于结构简单，运行和维护的成本也大大降低；(3)实现与电网的完全解耦，便于控制和分析其接入电网后的特性.

图1 永磁直驱风力发电机模型

PMSG定子与转子绕组的d-q轴电压为[16]

uds=-rsids+ωmxqiqs

，

(1)

uqs=-rsiqs-ωm(xdids-Ψq)

，

(2)

公式中：uds和uqs分别为d轴和q轴定子电压；ids和iqs分别为d轴和q轴定子电流；rs为定子电阻；Ψq为转子回路恒定磁通；ωm为转子角速度.

永磁风机网侧变流器等效电路如图，其有功功率和无功功率可以表示为[17]

pc=udcidc+uqciqc

，

(3)

Qc=uqcidc-udciqc

，

(4)

图2 永磁同步发电机等效电路

公式中：idc和iqc分别是网侧变流器dq轴坐标系下电流的直轴和交轴分量；udc和uqc分别是网侧变流器dq轴坐标系下的电压直轴和交轴分量.

换流器网侧电压与外部电网电压和相角存在如下关系：

udc=uisin(-θ)

，

(5)

uqc=uicosθ

，

(6)

将公式(5)和公式(6)带入到公式(3)中，可以得到永磁风机注入电网的有功功率为

Pc=-uiidcsinθ+uiiqccosθ

，

(7)

2 含PMSG电力系统负荷模式能量

2.1 含PMSG电力系统负荷模式能量函数的构建

为了能够准确从负荷角度分析PMSG参与振荡的物理过程，通过电力系统小干扰与能量相结合，构建含PMSG电力系统负荷模式能量函数.所得到的负荷模式能量函数可以针对PMSG并网系统发生低频振荡进行分析，在针对某关心模式，从负荷模式能量角度出发，负荷模式能量由同步机的状态变量与PMSG状态变量共同组成，找到负荷模式能量中具体风电状态量部分与同步机状态变量部分的联系，从而探究风机与同步发电机间的动态交互过程及风电状态量在低频振荡中如何参与和体现，实现对从负荷侧对含PMSG电力系统低频振荡特性解析.

针对含永磁风机的多机系统，发电机采用经典二阶模型，考虑发电机的阻尼，不计励磁调速器，负荷为恒阻抗负荷，不考虑风速影响设PMSG为恒风速运行.

对系统动态响应方程在平衡点处进行小干扰处理：

(8)

公式中：ΔX=[Δxδi，Δxωi，ΔxPMSG，Δxzi]T，Δxδi、Δxωi为同步机状态变量，ΔxPMSG为永磁风机的状态变量，Δxzi为其他状态变量；ΔUN=[Δu1，Δν1，Δu3，Δν2，……，Δun，Δνn，Δm1，Δm2，……，Δmn]Δun，Δνn为网络节点电压幅值和角度增量，Δmn为网络中其他代数变量；ABCD为系数阵.

n维系统状态变量解的一般形式为

(9)

公式中：φi，Ψi分别为右左特征向量.

网络节点电压的幅值和角度及其他代数变量为

ΔUN(t)=-D-1CΔx(t)=BΔx(t)

，

(10)

公式中：B=-D-1C.

对负荷所在母线电压增量表达式

(11)

(12)

公式中：Bi=B(i，：)，Bi+1=B(i+1，：)；c=Ψx0；d为状态变量个数；h为特征值个数；m为同步机状态变量个数；n为风机状态变量个数.

恒阻抗负荷模型有较好的调节效应，其模型函数定义为

(13)

公式中：V0代表负荷所在母线的稳态运行电压；PL0代表负荷在稳态运行时对应的有功功率；QL0代表负荷在稳态运行时对应的无功功率.

对恒定阻抗模型在平衡点处进行线性化处理：

(14)

含PMSG电力系统负荷i的模式能量表达式为

(15)

公式中：VLi-PMSG为PMSG并网电力系统负荷i的模式能量；ΔPLi为负荷i所在母线的功率增量；Δθi为负荷i所在母线的电压相角增量.

所得到的含PMSG电力系统负荷模式能量表达式可以分解为负荷模式能量的自相关与互相关的形式，即：

ΔVL-PMSG=ΔVLz-PMSG+ΔVLh-PMSG

，

(16)

公式中：ΔVLz-PMSG为负荷模式能量自相关模式；ΔVLh-PMSG为负荷模式能量互相关模式.

自相关模式势能指系统状态矩阵中特征值自身交互，组成自身二倍的形式，互相关模式能量指不同的特征值两两交互.负荷模式能量自相关部分由风电状态变量与同步机状态变量耦合后共同表征，在单一主导模式系统中可针对负荷模式能量的自相关部分对风机参与系统振荡过程进行解析[18].

1.2 基于负荷模式能量的系统小干扰稳定评价指标的构建

含PMSG并网电力系统中出现的小扰动有很多，例如风机风速的扰动，发电机的切除或接入，以及因为风吹摆动等引起输电线路电抗产生变化等，因此系统运行过程中小干扰必然存在.尤其对于含高比例PMSG并网系统而言，小干扰稳定性分析变得更加复杂，故对含PMSG系统进行小干扰稳定评价尤为重要.在系统发生低频振荡的过程中，同步发电机以及PMSG的模式动能与网络中的支路与负荷的模式势能相互转化[19-21].

从负荷模式能量角度衡量系统小干扰稳定程度，除了由负荷模式能量的振荡幅值大小决定，还取决于负荷模式能量振荡衰减的程度，因此本文构建基于负荷模式能量的系统小干扰稳定评价指标(Small Disturbance Stability Evaluation Index，SDSEI)对于系统小干扰稳定程度进行量化评价：

(17)

公式中：νL为负荷模式能量；νLmax负荷模式能量的最大值.

所建立的指标值是基于负荷模式能量振荡幅值与变化程度对系统小干扰稳定性进行评价，负荷模式能量振荡幅值选择负荷模式能量曲线第一摆幅值，负荷模式能量变化程度由负荷模式能量曲线第一摆极大值与第二摆极大值的差值代替.

根据DL/T 1234-2013《电力系统安全稳定计算技术规范》规定，系统一般临界阻尼比为0.03.对于系统临界阻尼比0.03下对应SDSEI值作为系统小干扰稳定临界值，并根据临界值判断系统小干扰稳定程度.若根据负荷能量计算出SDSEI值比小干扰稳定临界值小，说明系统小干扰稳定恶化；若根据负荷能量计算出SDSEI值比小干扰稳定临界值大，说明系统小干扰稳定改善.

3 仿真结果及分析

为了详细分析PMSG接入系统中负荷模式能量的变化规律及振荡过程风电参与振荡的特性，对系统小干扰稳定性进行评价.仿真如下：

3.1 算例1

在PSAT中建立如图3所示的四机两区域系统，发电机均采用计及阻尼系数的经典模型，负荷采用恒阻抗模型.

图3 四机两区系统

对四机两区进行小干扰分析，结果如表1所示.其中，模式3为系统主导振荡模式，为发电机1、发电机2与发电机3、发电机4之间的振荡，振荡模式阻尼比为0.03.

表1 四机两区系统振荡模式

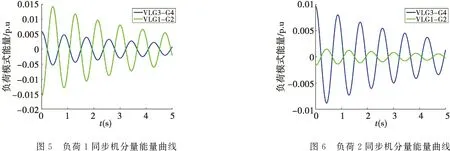
求取系统中负荷区域间振荡模式能量曲线如图4所示，由图可以得出负荷1与负荷2模式能量方向相反，区域间振荡模式将系统分为两个区域，其中负荷1属于区域1，负荷2属于区域2.

图4 四机系统负荷模式3能量曲线

进一步分析负荷模式能量方向相反的原因，对负荷模式能量中不同同步机成分进行分解如图5-6所示.由图5可知，在负荷1模式能量曲线中，{G1，G2}分量与{G3，G4}分量方向相反，与小干扰振型保持一致，并且{G1，G2}分量的大小要高于{G3，G4}分量，证明了位于区域1的负荷1受其区域中发电机{G1，G2}影响更大.由图6可知，在负荷2模式能量曲线中，{G1，G2}分量与{G3，G4}分量方向相反，与小干扰振型保持一致，并且{G3，G4}分量的大小要高于{G1，G2}分量，证明了位于区域2的负荷2受其区域中发电机{G3，G4}影响更大.

由图4可以得出负荷模式能量曲线，对系统SDSEI值进行计算，此时系统区域间振荡模式阻尼比为0.03，并以此值作为系统小干扰稳定临界值，对系统小干扰稳定进行评价.为了验证指标的准确性，将系统区域间振荡模式阻尼提升至0.07，得到负荷模式能量曲线如图7所示；将系统区域间振荡模式阻尼减弱至0.02，得到负荷模式能量曲线如图8所示.

计算三个系统的SDSEI值进行计算如表2所示.

表2 不同阻尼水平系统SDSEI值计算

由表2可以得出系统小干扰稳定临界值为0.174.当系统振荡模式阻尼水平下降时，对应SDSEI值减少，表征出系统小干扰稳定性恶化；当系统振荡模式阻尼水平上升时，对应SDSEI值增加，表征出系统小干扰稳定性改善.

3.2 算例2

为分析PMSG接入对系统的影响，将节点4的同步发电机替换为PMSG如图9所示.同步发电机均采用经典模型，并计及系统的阻尼，负荷设为恒阻抗负荷模型，PMSG采用PSAT中的五阶模型[22]，不考虑风速影响，设PMSG恒风速运行，PMSG的渗透率为29%.

对PMSG接入四机两区进行小干扰分析，结果如表3所示.其中，系统主导振荡模式为模式2，属于{G1，G2，G3，θPMSG}和{idcPMSG}之间的振荡，振荡模式阻尼比为0.03.

表3 四机两区系统并入PMSG的振荡模式

求取PMSG并网系统负荷的模式2能量曲线如图10所示.由图可以得出负荷1与负荷2模式能量方向相同，说明负荷1和负荷2属于同一区域.其中，负荷2模式能量的振荡幅值高于负荷1模式能量的振荡幅值，说明PMSG接入对负荷2的影响更大，表现为负荷距离风机接入位置越近，受风机的影响越大.

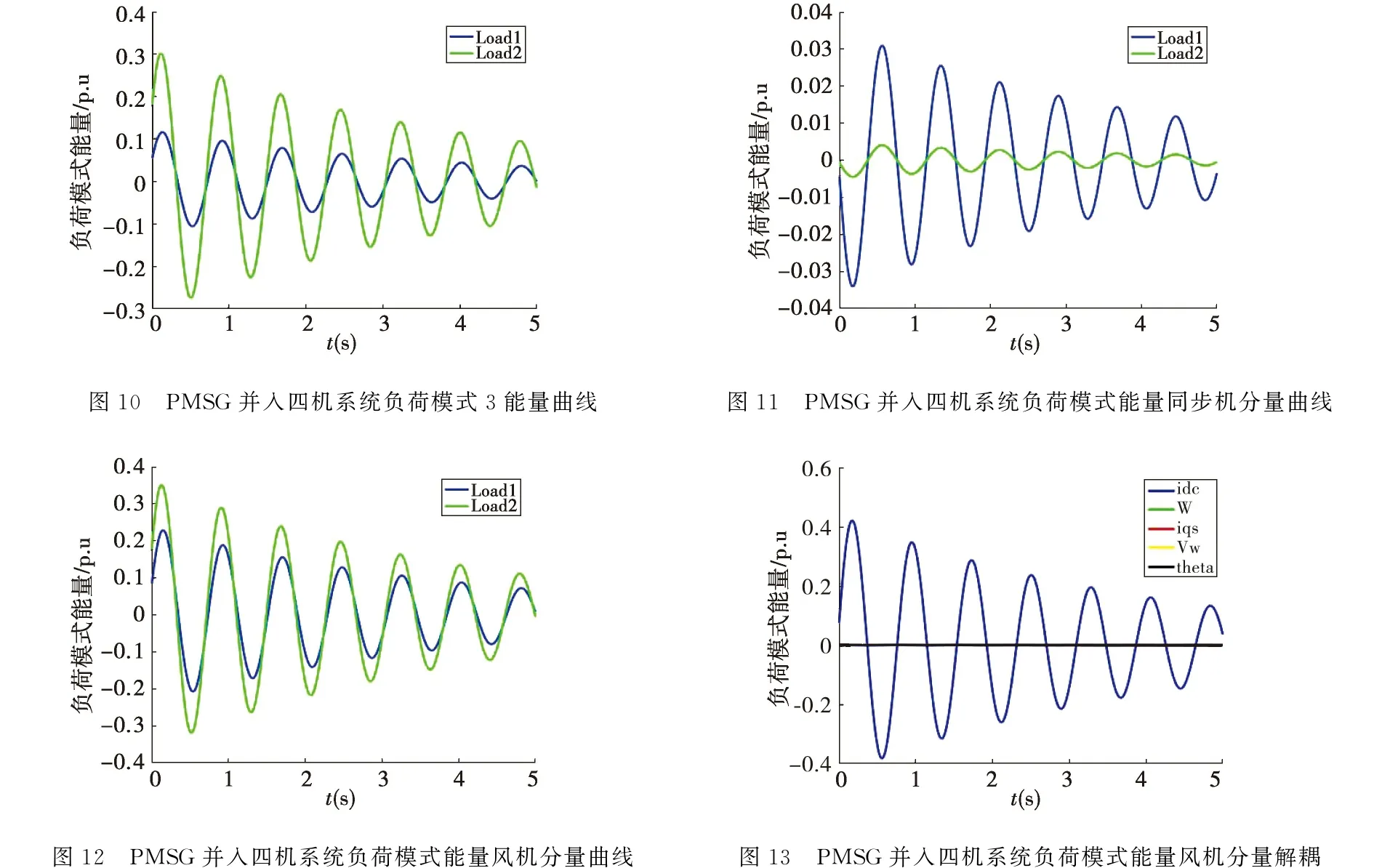
进一步分析PMSG并网负荷模式能量曲线，对负荷模式能量曲线中同步机分量与风机分量进行分解如图11～图12所示，并对负荷模式能量中的风机分量进行解耦如图13所示.由图可知，同步机分量与风机分量方向相反，且风机分量大于同步机分量，风机分量中idcPMSG占主导地位.由于负荷模式能量中同步机分量与风机分量方向相反，证明了PMSG接入对于系统小干扰稳定的影响与同步机对于系统小干扰稳定性的影响相反.负荷模式能量中风机分量振荡幅值大于同步机分量振荡幅值，说明了PMSG加入对于系统小干扰稳定的影响占主导地位.

由图10可以得出负荷模式能量曲线，对系统SDSEI值进行计算，此时系统区域间振荡模式阻尼比为0.03，并以此值作为系统小干扰稳定临界值，对系统小干扰稳定进行评价.为了验证指标的准确性，将系统区域间振荡模式阻尼提升至0.07，得到负荷模式能量曲线如图14所示；将系统区域间振荡模式阻尼减弱至0.02，得到负荷模式能量曲线如图15所示.

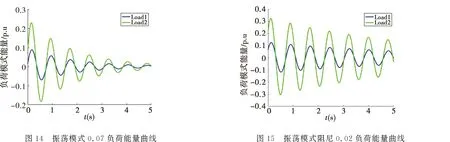
计算三个系统的SDSEI值进行计算如表4所示.

表4 不同阻尼水平系统SDSEI值计算

由表可以得出系统小干扰稳定临界值为0.17.当系统振荡模式阻尼水平下降时，对应SDSEI值减少，表征出系统小干扰稳定性恶化；当系统振荡模式阻尼水平上升时，对应SDSEI值增加，表征出系统小干扰稳定性改善.

4 结 论

本文利用能量函数与小干扰结合的方法对含高比例PMSG并网电力系统负荷模式能量进行了推导并仿真分析，从负荷角度对含高比例PMSG并网电力系统振荡特性进行解析，得到结论如下：

(1)高比例PMSG并网使得电力系统惯量降低，小干扰稳定性恶化，在负荷角度表征为负荷模式能量振荡幅值较传统电力系统负荷模式能量振荡幅值明显增高.

(2)负荷模式能量能够准确反应出高比例PMSG接入电力系统振荡特性的变化.其中，负荷模式能量中的风机成分能够表征出风机参与系统振荡的方式，同时证明了PMSG接入对于电力系统小干扰稳定影响处于主导地位.

(3)传统电力系统中负荷模式能量受距离近同步发电机影响大，而在高比例PMSG并网电力系统中，负荷距离风机接入点位置越近，受风机的影响越大，表征为负荷模式能量振荡幅值升高，负荷小干扰稳定性恶化严重.

(4)所构建的小干扰稳定评价指标能够基于负荷模式能量确定PMSG并网电力系统小干扰稳定临界值，对PMSG并网电力系统小干扰稳定特性进行评价.