基于系统导纳的并网逆变器谐振机理分析

苑忠奇，金国彬

(东北电力大学现代电力系统仿真控制与绿色电能新技术教育部重点实验室，吉林 吉林 132012)

近年来，分布式电源广泛应用于电力系统中，如光伏发电、风力发电等场合中，其中，并网逆变器扮演者重要的角色，将各类电源并入大电网中[1].目前，各种类型逆变器的控制方法已经比较成熟，在理想情况下保持稳定[2].在单台逆变器容量有限的情况下，广泛采用多台逆变器并联提高系统容量及效率等.但大规模逆变器并联与电网阻抗交互作用，在逆变器之间、逆变器与电网间引起串、并联谐波谐振问题[3].

并网逆变器系统稳定性分析方法主要有状态空间模型和阻抗模型[4]等方法.状态空间模型通常与时域仿真配合，通过求解系统特征值，分析系统参数对稳定性影响[5].但是这种方法作为一种数值计算，对参数依赖性以及系统复杂度要求较高，需要大量计算，无法揭示系统谐振机理[6].文献[7]中首次在直流-直流换流器系统中提出阻抗模型的概念.文献[8]将阻抗分析应用到并网逆变器系统稳定性分析中，将逆变器系统分为两个子系统分别建模分析系统稳定性.

基于阻抗分析方法，应用奈奎斯特判据分析系统稳定性，但是无法直接分析系统谐振频率，通过改进阻抗分析方法使阻抗比满足稳定性判据[9].针对多台逆变器并联，文献[10-11]通过建立多逆变器系统并网数学模型，揭示串、并联谐振机理，但是高阶系统计算复杂.文献[12]对每台逆变器建立并网电流数学模型，通过每台逆变器导纳对其他部分导纳的比值，分析每台逆变器的稳定性，但是，对系统系统稳定需要进行多次计算.文献[13]通过所有逆变器导纳与电网导纳的比值，应用奈奎斯特判据分析系统稳定性，但无法分析每台逆变器稳定性.文献[14]根据系统总电导和总电纳分析系统稳定性，得到逆变器并网谐振机理，但并未分析单台逆变器的阻尼特性.文献[15]利用全局导纳对并网逆变器并联系统的谐振机理进行分析研究，但未揭示单台逆变器对系统稳定性的影响.

本文针对多并网逆变器并联系统，在阻抗分析方法的基础上，建立多逆变器并联系统的系统导纳等效电路模型，分析系统导纳与系统稳定性的关系.在此基础上，不同工况下分析系统导纳中电导、电纳的作用，揭示系统谐振机理.最后，通过时域仿真验证该方法的有效性.

1 三相LCL型并网逆变器系统导纳建模

三相LCL型并网逆变器并联结构图如图1所示.每台逆变器经LCL滤波器接入公共连接点PCC.其中，Vdc为直流侧电源电压；VT为三桥臂功率开关管，不考虑死区带来的影响；L1n、L2n、Cn分别为n(n=1，2，…)台并联逆变器的逆变器侧电感、电网侧电感以及滤波电容，忽略寄生电阻的影响；Zg为电网阻抗，忽略电网电阻；ugabc为三相对称电网电压；i1，n、ig，n、ic，n分别为逆变器侧电感电流、网侧电感电流、电容电流；ig为并网侧总电流.

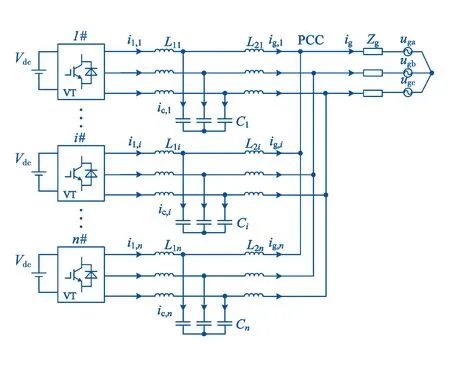
图1 并网逆变器并联系统结构图

三相LCL型并网逆变器的控制结构图如图2所示，以第i#台逆变器为例进行分析.采用静止坐标系αβ轴进行坐标变换，锁相环PLL的带宽设置为25 Hz，以避免低频段负阻尼的影响.因此系统可以看成是单入单出且解耦的，以其中一相为例进行说明.其中，upcc为公共连接点PCC点电压，iref为参考电流.upcc经过锁相环PLL为iref提供并网电压相角θ，采样信号ig与参考信号进行比较，经准比例谐振QPR电流控制器后与电容电流ic比较后载入脉冲宽度调制PWM.PWM采用对称采样方式，即采样频率fs等于开关频率fsw.

根据图2所示，得到计及延时的三相LCL型并网逆变器系统的传递函数结构图，如图3所示.其中kad为电容电流反馈系数.

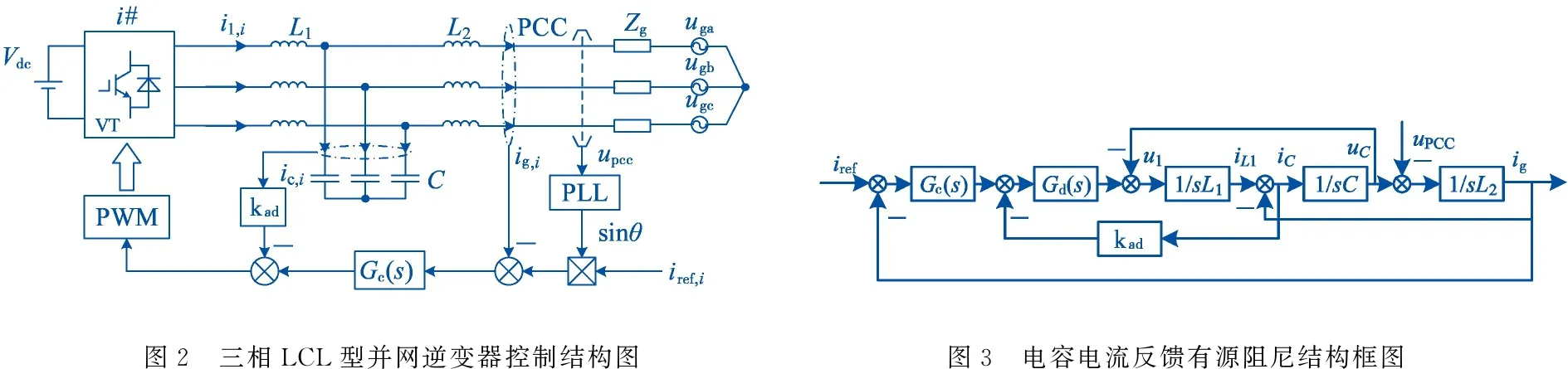
如图3中所示，Gd(s)为并网逆变器系统延时环节，包括计算延时和采样延时环节，如公式(1)所示.

(1)

(2)

公式中：Ts为采样时间，Ts=1/fs；s为拉式算子.Kp、Kr分别为比例系数、谐振系数；ωo为基频角频率，ωo=2πfo，fo=50 Hz；ωi为控制带宽，ωi设计为π rad/s以降低基频变化对系统稳定性影响.

三相并网逆变器系统中从PCC端向逆变器侧看去的等效导纳模型如图4所示，逆变器侧等效为电流源Gcl(s)·iref和输出导纳Yo(s)的并联，网侧为电网阻抗与电压串联.

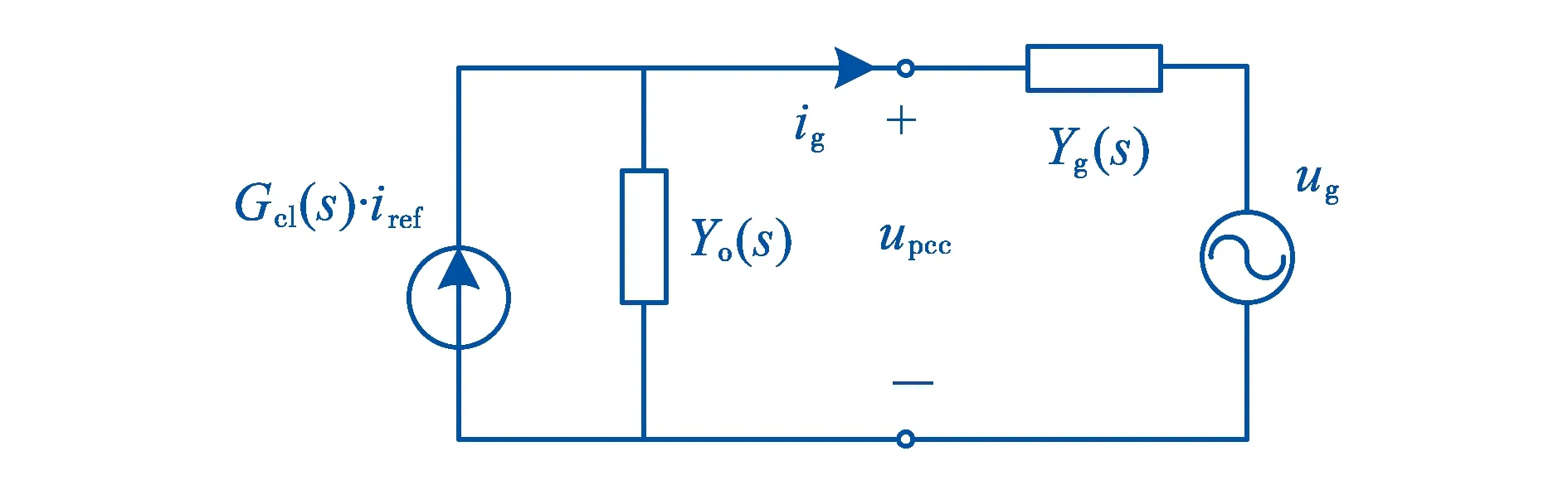
图4 单台并网逆变器系统的等效导纳模型

首先考虑单台逆变器系统，假设电网电压是稳定的，不计电网电压背景谐波；并且当不计电网阻抗时，逆变器是稳定的，即要求逆变器系统闭环传递函数Gcl(s)是稳定的.根据图4所示的等效电路，逆变器输出电流为

(3)

基于假设条件和公式(3)，当且仅当逆变器导纳与电网导纳之比Yo(s)/Yg(s)满足奈奎斯特准则时，单个逆变器并网系统将保持稳定.

根据图3结构图化简可得，电压upcc和电网电流ig之间的逆变器输出导纳Yo(s)可推导如公式(4)所示.

(4)

在上述单台逆变器分析的基础上，分析多台逆变器并联时系统稳定性.如图1所示的多台逆变器并联的等效导纳电路图如图5所示.

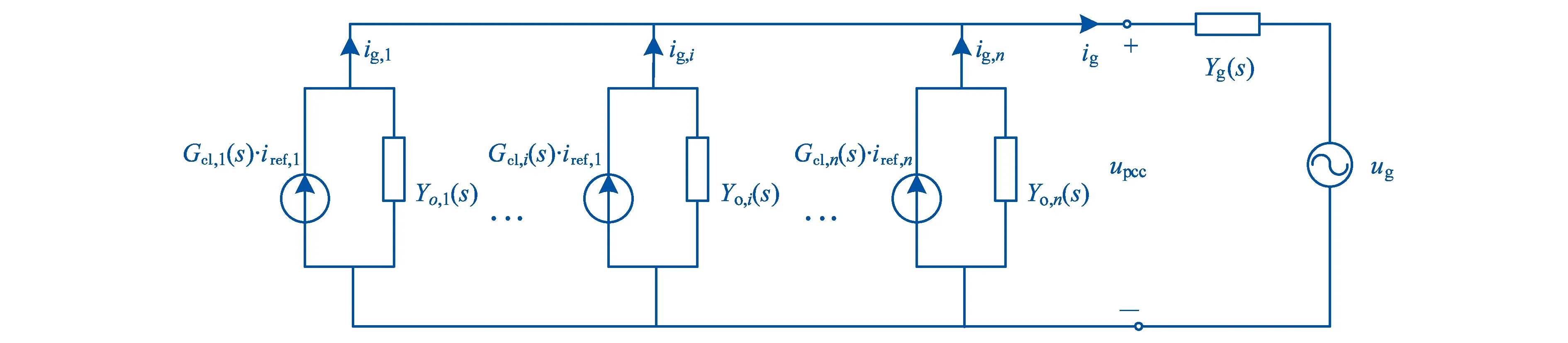
图5 多逆变器并联系统等效导纳电路

对图5所示电路应用节点电压法列写方程，如公式(5)所示.

(5)

为消除电压upcc项，根据基尔霍夫电流定律，第i#台逆变器的并网电流如公式(6)所示.

ig,i=Gcl,i·iref, j-Yoc,i·upcc

.

(6)

联立公式(5)、公式(6)推导可得第i#台逆变器的并网电流如公式(7)所示.

(7)

(8)

从公式(7)中可以看出，多台逆变器并联时，第i#台逆变器的输出电流取决于三部分，一是取决于逆变器自身的等效电流，二是取决于其他逆变器的等效电流，三是与电网电压的交互作用.假设每台逆变器的闭环传递函数Gcl，i(s)提前设计为单独稳定，且电网稳定.通过分析每台逆变器的稳定性，可以分析整个逆变器系统的稳定性.进行n台逆变器分析后，如果所有n台逆变器都是稳定的，则多并联逆变器并网系统是稳定的.从多台并网逆变器系统的阻抗分析法可以看出，必须对n台逆变器进行n次分析，才能确定整个电网系统的稳定性，因此不可避免的会增加计算量.当逆变器台数和电网阻抗发生变化时，需要对公式(7)、公式(8)进行重新计算.

2 并网逆变器系统的导纳特性条件

逆变器的输出导纳可以等效为“RLC”串联电路，电网因其性质不同本文等效为“RL” 串联电路，因此并网逆变器系统等效电路图如图6所示.

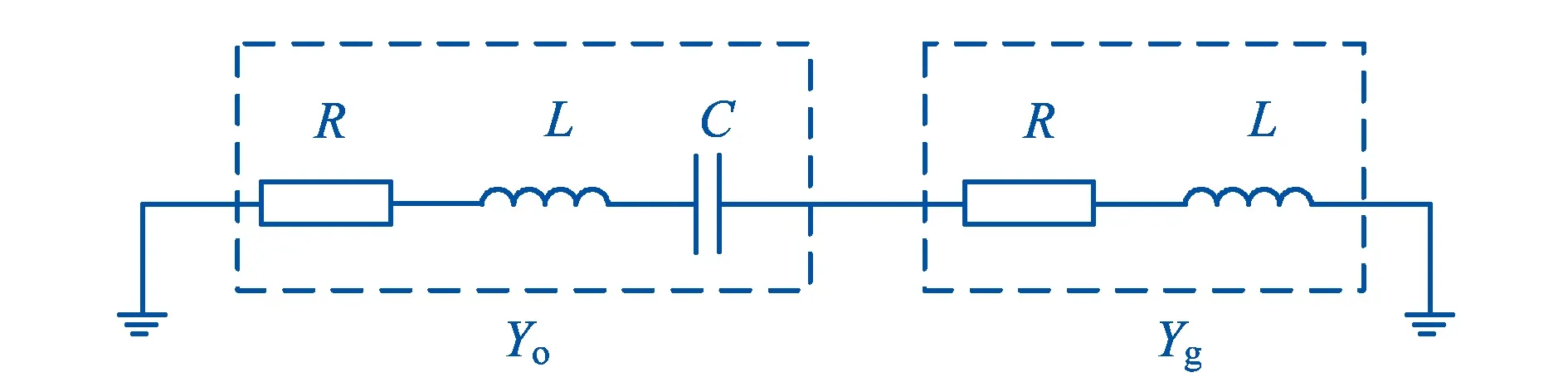
图6 并网逆变器系统等效电路图

从图6中可以分析，系统导纳可以等效成二阶振荡电路，若系统等效电导G是非负的，则系统稳定；相反，若G为负值，则系统可能处于不稳定状态.

并网逆变器系统的系统导纳可以表示为

(9)

由公式(7)进一步变形可得：

(10)

根据公式(10)可以分析，电网导纳Yg为无源元件，不含右半平面RHP极点.考虑电网电压稳定，等效电流源Gcl，i·iref，i无右半平面极点，则逆变器输出电流与1/Ys有关，即与Ys的零点有关.

根据图6、公式(9)和公式(10)系统导纳用电导和电纳表示为

Ys=G+jB

，

(11)

公式中：电导G为系统阻尼水平；电纳B为系统可能出现的谐振点.

系统可能出现的情况如下所示：

(1)电导G始终为非负，不论系统是否存在谐振点，系统始终保持稳定；

(2)若系统不存在谐振点，即系统为容性或感性，不论G为何值，则系统稳定；电导G小于0时，若系统谐振点不位于此区间，系统仍保持稳定；

(3)电导G小于0时，且系统谐振点位于此区间，则系统不稳定.

根据上述分析，由公式(11)中Ys可以分析并网逆变器系统稳定性.与公式(8)的比值形式稳定性分析相比，以系统导纳分析系统稳定性，从系统电导G和电纳B分析系统阻尼和系统谐振点.系统导纳方法在计算量方面大大降低，同时分析了每台逆变器对系统稳定性的贡献.此外，当电网阻抗和逆变器参数发生变化时，可以很方便地观察到系统导纳特性的变化，包括系统阻尼水平和谐振点位置的变化.

3 并网逆变器谐振机理分析

由图3所示，可以化简推导出系统开环传递函数

(12)

当不计电网阻抗时，根据表1所示参数以及公式(11)画出系统bode图，如图7所示.从图中可以看出，幅值裕度和相位裕度满足要求，此时系统保持稳定.

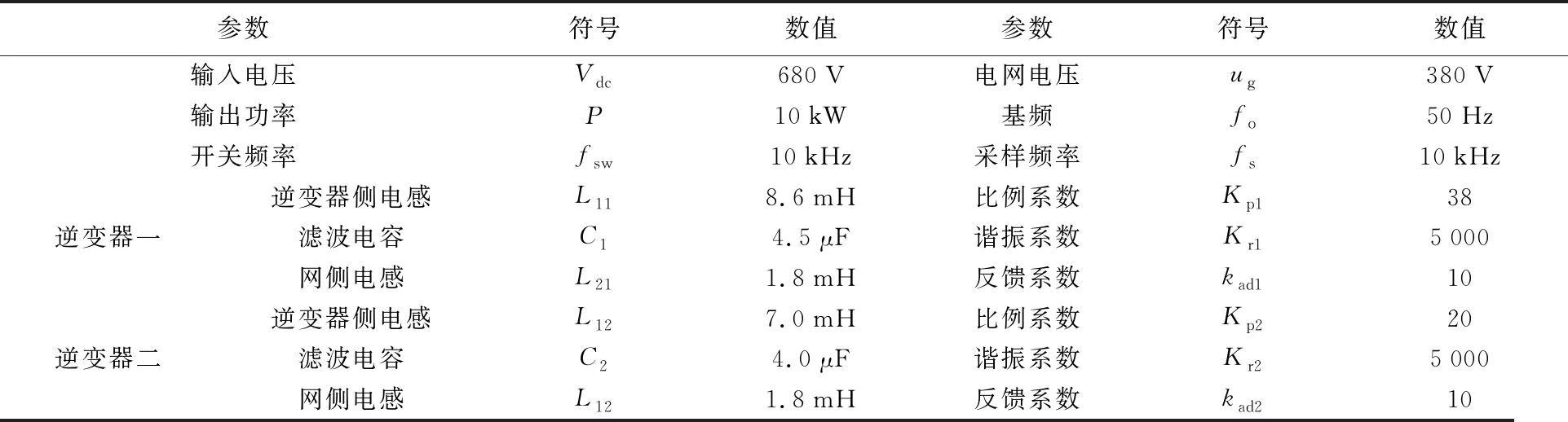
表1 并网逆变器系统的各项参数

图7 不计电网阻抗时系统开环bode图

3.1 不同电网阻抗

电网阻抗变化时系统导纳特性图及部分放大图如图8所示.由于电网阻抗只影响电纳，因此系统电导保持不变，从图8(a)中可以看出，电导在一段区间内为负阻尼.当电网阻抗Lg=0.1 mH时，由于虚部电纳始终为负值，不存在谐振点，因此系统恒稳定.

如图8(b) 中所示，当电网阻抗Lg=1.8 mH时，存在虚部为0的点，此时谐振点位于负阻尼区间，系统不稳定.当电网阻抗进一步增大时，Lg=3.0 mH，虚部电纳继续上移，谐振点仍位于负阻尼段，系统仍不稳定.

图8 不同电网阻抗时系统导纳特性及局部放大图

3.2 多逆变器并联

首先考虑逆变器参数一致时并网逆变器系统，以表1参数中逆变器一为例进行分析.逆变器台数n=2，4时的系统导纳特性图及局部放大图如图9所示.从图中可以看出，当n=2时，系统谐振点频率降低，谐振点进入负阻尼区域发生振荡.当逆变器台数继续增加时，n=4，谐振频率继续降低，系统有可能发生失稳，振荡频率约为1 150 Hz左右.

图9 多逆变器并联时系统导纳图

进一步分析逆变器参数不一致时逆变器并联谐振机理.以表1中2台逆变器一和1台逆变器二为例进行分析.并网逆变器系统导纳特性图如图10所示.从图中可以看出，并网逆变器系统存在多个谐振点，只有一个谐振点在负阻尼区主导系统谐振，此振荡频率为1 180 Hz.逆变器一导纳Y1、逆变器二导纳Y2和电网导纳Yg的特性图及局部放大图如图11所示.逆变器一的电导为-0.017，逆变器二的电导为0.003 5，电网导纳为0，由于系统阻尼为负，因此逆变器一主导系统谐振.

图10 系统导纳特性图

图11 逆变器一、二和电网导纳特性图

4 算例分析

由上述谐振机理分析可知，可以清楚直观地量化并展现系统导纳随频率的变化趋势，具有明确的物理意义.而时域仿真法通过仿真软件建立电力电子逆变器系统仿真模型以分析系统稳定性和谐振特性，实质是对系统微分方程组进行数值积分从而求解系统运行曲线，并能够直观准确的提供电网波形信息.但其无法量化分析谐振发生机理，因此通常作为验证理论分析结果的一种辅助手段，与阻抗分析法配合使用进而全面深入地研究谐振机理问题.因此为了验证谐振机理理论分析的正确性，以表1中所示逆变器参数为例，在MATLAB/Simulink中搭建并网逆变器系统仿真模型进行验证.

4.1 不同电网阻抗

不同电网阻抗时电网电流波形图如图12所示.图12(a)中，在0.4 s时改变电网阻抗，在0.4 s前电网阻抗Lg=0.1 mH，电网电流波形稳定；0.4 s后电网阻抗Lg=1.8 mH时很快发生振荡，由快速傅里叶变换FFT分析谐波畸变率THD为7.17%，振荡频率为1 450 Hz.图12(b)显示0.4 s后电网阻抗Lg=3.0 mH时，电网电流波形发生振荡，振荡频率为1 330 Hz左右.系统振荡频率随着电网阻抗的增加而降低.这与第二节中电网阻抗变化时机理分析一致.

图12 不同阻抗时电网电流波形图

4.2 多逆变器并联

如图13所示为逆变器参数一致时并联电网电流波形图，其中以一相电流波形为例进行分析.图13(a)所示两台逆变器并联时，并网电流发生振荡，电流谐波畸变率THD为10.3%，振荡频率为1 300 Hz左右.图13(b)所示4台逆变器并联时，可以看出，电网电流很快发生失稳，振荡频率约为1 165 Hz.上述分析表明，这与第二节中多逆变器并联时谐振机理分析一致.

图13 多逆变器并联时电网电流波形图

如图14所示为逆变器参数不一致时，2台逆变器一与1台逆变器二并联时电网电流波形图.由前述分析可知系统阻尼仍为负，仍处于谐振状态，电流谐波畸变率THD为6.05%，与图13(a)相比有所降低，这是因为逆变器二为系统提供的正阻尼所致.

图14 逆变器参数不一致时电网电流波形图

5 结 论

本文针对多逆变器并联系统的谐波谐振问题，基于阻抗分析法建立系统导纳模型，分析系统电导、电纳与系统稳定性关系，分析不同工况下谐振机理，以及单台逆变器对系统的阻尼贡献，并进行仿真算例分析，得到主要结论如下：

(1)与基于阻抗比值分析谐振机理相比，基于系统导纳模型的谐振机理分析计算较为简单，通过系统导纳的电纳、电导可以进行谐振机理分析.

(2)系统导纳的电导体现系统阻尼水平，电纳反映系统可能出现的谐振点.若电导为负且存在谐振点，则系统发生谐振甚至失稳；若电导特性始终保持为正，则系统恒稳定.基于系统导纳可以有效分析每台逆变器对系统的阻尼贡献.

(3)在电网阻抗、并网逆变器数量变化时等工况下，系统阻尼和谐振点会相应发生变化，时域仿真验证了该方法的有效性.