基于Pareto 的电池容量衰退权衡优化控制策略

林歆悠，叶常青，苏 炼

福州大学机械工程及自动化学院，福州 350002

随着能源问题和环境问题越来越受到大众的关注，而汽车作为消耗石油和有害气体排放的主要源头之一，未来的汽车工业开始经历从液体燃料动力系统到电气化动力系统的转变[1].由于混合动力汽车具有不止一个能量源，因此需要设计一种能量管理策略(Energy management strategy,EMS)以协调多能源之间的功率分配，从而实现插电式混合动力汽车的最优经济性.

国内外的许多研究人员已经提出了大量的EMS，从时间尺度的角度看，EMS 可以分为离线能量管理策略、在线能量管理策略.离线能量管理策略主要有线性规划、动态规划(Dynamic programming,DP)，粒子群算法、遗传算法以及凸规划[2-4]等；在线控制策略又包括电量消耗和电量维持策略[5]、模糊逻辑控制[6]、等效消耗最小化策略(Equivalent consumption minimization strategy,ECMS)[7]、神经网络控制[8]、庞特里亚金最小原理(Pontryagin’s minimum principle,PMP)导出的策略[9]、由DP 导出的策略[10]等.而目前很多研究只解决功率分配问题，并没有考虑动力电池等元器件的使用寿命，这种忽视将导致车辆总生命周期成本增加.因此，最近一些EMS 将车辆能量储存组件的性能约束纳入优化约束.

随着车辆储能系统的研究深入，锂离子电池具有高能量、高功率密度的特点[11]，是新能源中首选的储能技术；由于汽车对耐久性和稳定性要求较高，电池长期的循环和贮存性能越来越受到人们的关注.然而，电池寿命是先进储能系统总寿命周期成本的主要不确定因素之一，因此，锂离子电池的性能衰退以及健康管理一直以来都是一个很大的研究课题[12-14].一般来说，电池老化表现为储存能量和提供能量的能力下降，这与容量损失和内阻增加有关.电池的老化，主要表现为阳极和阴极的老化，它的基本原理是：电解质和阳极之间形成了一个保护层，即固态电解质界面膜（Solid electrolyte interface,SEI），进而随着SEI 的形成以及增长导致了阳极的老化、活性锂及可移动锂离子的损失，最终导致了自我放电和不可逆的电池容量衰退.混合动力汽车的燃油经济性、回收能力和驾驶性能受其能量储存系统的比功率和能量容量的显著影响[15].锂离子电池的老化模型可分为物理化学模型和经验模型两大类.基于物理化学建模的锂离子电池文献相当广泛.第一个模型具有两个复合电极和一个分离器，并进一步扩展，以考虑在电池处于充电模式时，在负电极表面附近持续出现非常缓慢的溶剂扩散/还原的情况下，具有循环数的电池的容量衰减[16].文献[17]提出了一种多目标最优控制问题，目的是对功率分流插电式混合动力汽车(Plug-in hybrid electric vehicle,PHEV)的低功率进行管理，使健康退化和能源消耗成本最小化，通过阳极侧阻膜的形成，定量研究了电池的老化性能.文献[18]根据一维ECMS 和电池退化模型研究了一辆具有双行星齿轮组结构的混合功率分配PHEV 的结构设计和控制对燃料消耗和电池退化的影响.文献[19]针对具有大电池组的单轴并联插电式混合动力客车，利用锂离子电池的容量损失模型来模拟循环寿命和日历寿命，通过跟踪两个参考轨迹来调整电池的荷电状态(State of charge,SOC)和有效的安培小时流量，并设计了一种PMP 的在线协调优化方法实现降低能耗和电池退化总成本的目标.林歆悠等[20]为提高插电式燃料电池混合动力汽车的经济性和燃料电池耐久性，将燃料电池开路电压衰退转化成等效的氢气消耗加入到目标价值函数之中，制定了等效氢气消耗最小的反馈优化控制策略.

额外的优化目标会造成严重的计算负担，因此生成可信Pareto 解比较困难.本文所构建的PHEV 能量管理问题需要使油耗及电池衰退两个目标最小，那么在燃油经济性和电池衰退之间就会有一个基本的权衡，然而，现实的情况是，电池寿命会大幅降低，而燃料消耗只会减少一点点.据作者所知，现有文献对于最优权重的选择阐述很少，因此本文构建了考虑燃油经济性和电池寿命的目标函数加权组.通过引入权重系数将多目标优化问题转化为单目标问题，采用动态规划算法求解实现全局最优，通过对比不同权重下的油耗及电池损耗选择最优权重系数，最后运用ECMS验证了所提策略的有效性.

1 电池容量衰退模型的构建

在前言中，已经详细介绍了电池性能衰退的几种情况及基本原理，由此，电池的衰退反映在工作状态中就表现为衰减的放电效率及缩短的纯电动里程.据此，在电池的循环工作中，首先对影响电池衰退的因素进行分析，再根据电池的特性构建电池的性能衰退模型.

1.1 电池容量衰退的影响因素

通常情况下，电池衰退可分为可逆衰退和不可逆衰退[21]，目前，对电池寿命衰减的研究一般是针对不可逆容量衰退进行的，造成电池容量不可逆衰退的原因除了其自身因素外，还有很多因素，比如电池生产时的状况、电池放置时间、电池SOC、工作的环境等等，本节所涉及的主要因素为电池的放电深度、充放电倍率、温度及充放电截止电压.

1.1.1 放电深度

放电深度指的是放出的电量占总电量的比值，通常用DOD 表示，如DOD=0.4，则表示动力电池由满电时的SOC=1 放电到SOC=0.6 时所放出的电量.相关文献研究表明，锂电池的循环寿命随着DOD 的逐渐增加而逐渐减少[21]，如图1 所示.

图1 电池循环次数与放电深度的关系Fig.1 Relationship between the number of battery cycles and the depth of discharge

1.1.2 充放电倍率

电池的充放电倍率指的是充放电电流与电池额定容量的比值，常用Ic来表示，充放电倍率越大，电池容量衰退越快，如果充放电倍率过大，则会导致动力电池的损坏，如图2 所示.

图2 不同放电倍率下的电池衰退率Fig.2 Battery decay rate at different discharge rates

1.1.3 温度

电池性能衰退在一定程度上也受温度的影响，据研究表明，锂离子电池的工作温度的大概范围是-20 ℃～60 ℃，而其最佳的工作温度范围在20 ℃～40 ℃，如图3 所示，此时的锂电池具有最大的循环寿命，低温或者高温都会对动力电池的寿命有比较大的影响[22].

图3 不同温度下的锂电池寿命曲线Fig.3 Lithium-ion battery life curve at different temperatures

1.1.4 充放电截止电压

图4 为某锂离子电池在不同充电截止电压下的容量衰退曲线，众所周知，过充电及过放电都会导致不可逆的电池容量衰退，由图可知电池容量衰退的速度随着充电截止电压的增加而变快；同理，当电池放电时，电池容量衰退的速度随着放电截止电压的减少而变快.

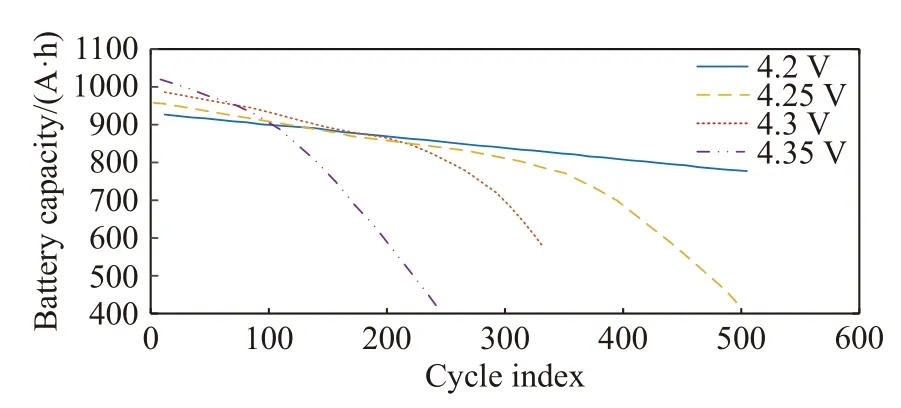
图4 不同充电截止电压下的电池容量衰退Fig.4 Battery capacity degradation at different charge cutoff voltages

综上，影响电池性能衰退的因素很多，但实际生产过程中，厂家会对电池的一些参数进行规定以保证安全性.本文考虑从温度和充放电倍率对锂离子动力电池循环寿命的影响进行分析.

1.2 电池的热模型

基于电池的热动力学和电池的等效电路模型，依据已有电池热模型，假设电池组可以看作一个热量均匀法的整体，那么电池的发热和温度变化率可以表达如下：

1.3 电池的容量衰退模型

电池的老化来源于复杂的机理，造成了电池的容量衰退和内阻的增加.在车辆的运用中，电池的老化有两种情况，一种是储存时的老化，另一种是循环工作时的老化，本节主要考虑的是车辆工作时的电池循环老化.电池的容量衰退模型是基于电池老化研究的基础上所开发出来的.由于在简单性和准确性之间的良好折衷，本节电池的容量衰退模型将会运用与最优控制问题相联系的半经验模型，其通用模型[23].

其中，Qloss是电池容量相对于额定容量损失的百分比；B是指前系数；Ea是活化能，J·mol-1；R是气体常数，J·(kg·K)-1；Ah 是安时通量，A·h；z是幂率因子.

因上述的通用模型是电池在实验室环境中测得的，与实际情况有所差别，因而在该通用模型的基础上考虑到电池SOC、平均充放电倍率对电池老化的影响对其进行了修正[24]，修正后的老化模型具有如下的形式：

2 考虑电池容量衰退的PHEV 控制策略的构建

电池的性能衰退通常包含电池容量的衰退及电池内阻的增加，本节主要针对电池的容量衰退进行分析，电池容量衰退表现出的就是电池寿命的衰减.通常电池的使用寿命被定义为电池从其初始值容量下降到其80%容量时的寿命[25]，那么相对于电池的额定循环寿命，电池寿命可以用电池达到寿命结束时的累积放电量来表征.电池的额定寿命从累积总电量的角度可以表示为：

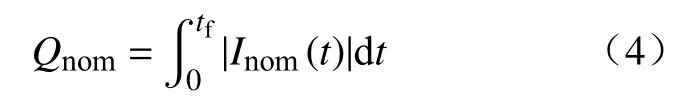
其中，Inom是电池额定工况下的充放电电流，tf是电池寿命终止时间.

电池实际运行过程中，它所处的环境就不一定是标况下的环境，由此，引入严重程度因子 σ的概念，用来量化表达相对于额定条件，实际条件下对电池老化影响的程度[26]，它的表达式如下：

其中，Qact是电池寿命结束时实际的累计总电量，I为实际充放电电流.当电池经历一个更严重的负载循环时，严重程度系数大于1，预期寿命更短.此外，严重程度因子也可根据上述的电池老化模型的经验来获得，电池寿命终止可以定义为20%的容量损失，本节定义的额定工况中Ic,nom为1C，温度为25 ℃，SOC为0.5，则电池的额定寿命和实际寿命表达式如式（6）所示:

由此，我们定义有效的累计电量如式（7）所示：

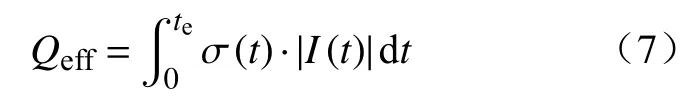
其中，te是结束时间，s；有效累计电量给出了相对于额定寿命的电池损耗，因此，当Qeff=Qnom时，电池寿命终止.由此，使电池老化最小化的目标就可以转换为使Qeff最小化.

根据上述可知，本文的PHEV 能量管理问题可以表述为一个使油耗最小同时电池容量衰退也最小的权衡优化控制问题.该问题是一个多目标问题，通过引入权重系数将该问题转化为单目标问题，其中的状态变量为SOC 和电池温度，控制变量为电机转矩.电池温度、SOC 及严重程度系数的三维关系图如图5 所示.

图5 电池SOC、温度和严重程度系数关系图Fig.5 Chart of battery SOC,temperature,and severity coefficient

由于状态变量有两个，一般情况下的动态规划已具有较大的计算量，这就导致计算时间更长，不论是在仿真还是实际操作过程中都不太利于控制策略的改善.为了避免该问题，同时电池的温度与电流及电池的充放电倍率之间具有一定的关系，那么可以通过充放电倍率间接地评价电池的寿命，则在不同的温度下，严重程度因子与电池SOC及电池的充放电倍率的关系如图6 所示.

图6 不同温度下的严重程度系数关系图.（a）15 ℃；（b）30 ℃；（c）45 ℃；（d）60 ℃Fig.6 Relationship diagram of severity coefficients at different temperatures：(a) 15 ℃；(b) 30 ℃；(c) 45 ℃；(d) 60 ℃

这里简化价值函数，不考虑电池温度这一状态变量，在电池温度为25 ℃下构建包含电池损耗的目标价值函数，具体如下：

其中，第一项为油耗价值成本（包含电池的等效油耗），第二项为电池损耗价值成本，α(0≤α≤1)为权重系数,为燃油消耗率，F为仅考虑燃油消耗的评论燃油消耗率，Qeff,diff为考虑最佳电池寿命的最小有效安时量.当 α=1，此时不考虑电池的老化，只考虑油耗的情况，是最好情况下的油耗及最坏的情况下的电池老化.理论上，最低老化的情况下，即 α=0，车辆将作为一辆传统汽车使用而不使用电池，这将产生零老化效果和最大的燃油消耗.为了上述的油耗成本及老化成本两项在数值上具有可比性，对它们进行了标准化，采用差值标准化，即通过最低点和理想点的最优函数值的差值进行标准化，进而给出最优目标函数在Pareto 最优集内变化的区间长度.该标准化方法通过目标函数在Pareto 最优集上变化的真实区间对目标函数进行标准化，得到了比较理想的归一化结果.直观上不难看出，归一化后的两项将以0 和1 为界，在加权目标函数中具有可比性.系统所受的约束如下：

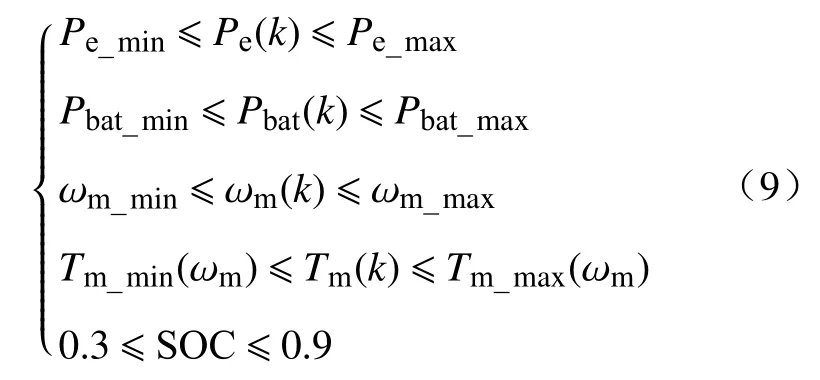
其中，Pe_max、Pe_min分别为发动机最大功率和最小功率，kW；Pbat_max、Pbat_min分别为充电功率的最大值和最小值，kW；ωm_max、ωm_min分别为电机转速的最大值和最小值，r·min-1；Tm_max、Tm_min分别为电机最大转矩和最小转矩，N·m.

动态规划作为一种保证全局最优性的方法，被应用于最优控制问题的求解.我们将动态规划用于求解上述所构建的控制问题，此处简要说明其过程.动态规划需要系统的离散时间描述和决策变量的离散值集，如式（10）所示：

其中，Δt是采样时间，s；NT是样本中优化时域长度，其计算如下：

系统的状态是离散的，只能取最大或最小值间有限数量的值中的一个.该值的集可以定义为：

其中，j=1,···,NSOC，NSOC是SOC 在每个时间步长可用的网格点数量，本章的控制输入电机转矩Tm也需要在允许的范围内进行离散化：

其中，Nu是每个时间步长可用的控制点数量，其控制问题就是使总成本最小化，其表达式如下：

本节所采用的DP 求解最优控制下的发动机转矩及电机转矩的流程图如图7 所示.动态规划算法确定最佳的电荷状态序列，然后作为结果，获得驱动电机扭矩.在本文中，使用Matlab 编写动态规划程序进行全局优化求解.

图7 考虑电池容量衰退的权衡控制策略DP 求解流程图Fig.7 Solution flow chart of the trade-off control strategy DP considering battery capacity decline

3 验证和结果分析

为了模拟一些激进型、高速或高加速的驾驶行为，体现所制定策略的优化效果，这里采用US06 驾驶循环工况进行验证.根据本论文所构建的基于Pareto 的电池容量衰退权衡优化能量管理策略，通过重复US06 工况，分析不同权重因子（0.1≤α≤1）下的权衡优化电池容量衰退和发动机油耗的Pareto 非劣最优目标域的性能，其结果如表1 和图8 所示.

图8 7 个US06 工况下不同权重时的DP 解Fig.8 DP solutions of seven US06 operating conditions with different weights

表1 7 个US06 工况下的仿真结果Table 1 Simulation results of 7 US06 operating conditions

由上述结果可知，当权重系数由1 变成0.9时，Qeff由257.6 A·h 减少到137.9 A·h，减少了46.4%，即极大地减小了电池寿命衰减的程度，而耗油量由3.941 L 增加到3.983 L，燃油消耗量只增加了1%，因而，只增加微小的燃油消耗，却能极大地减小电池老化的影响；再比如，当权重系数由1 变成0.3 时，Qeff由257.6 A·h 减少到7.7 A·h，减少了97%，但是燃油消耗量由3.941 L 增加到4.326 L，油耗增加了8%，此时虽说极大地降低了电池的老化影响却牺牲了较多的燃油经济性，这有背于所设计的控制策略初衷，因而本节选用 α=0.9作为最优权重系数.注意，因 α=0时代表车辆以传统的汽车模式进行工作，因而没有电量的消耗，所以表中并未列出.

为了进一步分析观察控制策略在最优权重系数下的行为，根据上述分析时选用的7 个US06 工况片段，其在权重系数 α的值分别为1、0.9、0 时的电池SOC 曲线如图9 所示.由图9 可知，α=0时，电池是不工作的，因而其电池的荷电状态未发生改变；α=0.9时的SOC 曲线要比 α=1时的SOC 曲线平缓一些，这说明有权衡时的电池的放电比没有权衡时的电池放电要平缓，这对减慢电池的衰减有利.

图9 不同权重下的SOC 曲线.（a）车速示意图；（b）SOC 变化曲线Fig.9 SOC curves under different weights: (a) speed diagram;(b) SOC change curve

图10 为不同权重下的充放电倍率和严重程度系数，从图10(a)中可以看出，在考虑到电池的衰退时，电池的充放电倍率要明显低于不考虑电池衰退时的充放电倍率.由1.1.2 节中的影响因素可知，电池的充放电倍率越大，电池容量衰退越快，也即电池老化的越快，因而本节提出的考虑电池衰退且权重因子 α=0.9时的策略能够在保证车辆的燃油经济性的牺牲几乎可以忽略不计的情况下明显地降低电池老化的速度，即明显地降低电池性能衰退的程度.此外，图10(b)进一步说明了所选用的策略在该权重因子下的有效性.由第2 节可知，严重程度系数表示实际条件影响电池老化的程度，标况下，电池随着使用时间的增加也会逐渐老化，但不同工况下使用电池，其相对于标况下的老化速度要更快，即 σ越大，Qeff越大，其相对于额定寿命的电池损耗越快，达到Qeff=Qnom的速度也越快，预期寿命越短.α=0.9时的严重程度系数要明显的小于 α=1时的严重程度系数，因而有权衡优化时的电池老化速度比无权衡优化时的老化速度要慢，电池寿命比无权衡优化时的寿命要长.

图10 不同权重下的仿真结果.（a）充放电倍率；（b）严重程度系数Fig.10 Simulation results under different weights: (a) charge and discharge ratio;(b) severity coefficient

有无权衡优化时的电机、发动机转矩对比如图11 所示，相比于无权衡优化时电机转矩，有权衡优化时的电机输出转矩减小，说明电池的输出功率减小，电池的放电倍率减小，进而电池的性能衰退减慢；而相比于无权衡优化时的发动机转矩，有权衡优化时的发动机输出转矩有所增大，进而导致油耗有所增加，但由表1 可知，其油耗只增加了1%，几乎可以忽略，但Qeff却降低了46.4%，因而以极小的油耗牺牲换取较大的电池寿命提升是可取的，说明该策略是有效的.

图11 不同权重下的仿真结果图.（a）电机转矩；（b）发动机转矩Fig.11 Simulation results under different weights: (a) motor torque;(b) engine torque

依据上述所构建的策略在DP 求解下的结果，为进一步说明本文构建的策略的有效性，选取上述结果中权重 α=0.9时的策略在相同工况下进行在线的ECMS 求解，所得结果与此权重下的DP 求解结果进行对比分析，结果如图12～14 所示.图12为权重 α=0.9时，在相同工况下不同方法的SOC曲线，由图可知，两种方法下的SOC 曲线非常接近，此外，两种方法下的充放电倍率及严重程度系数 σ的仿真结果如图13 所示.

图12 不同方法下的SOC 曲线Fig.12 SOC curves under different methods

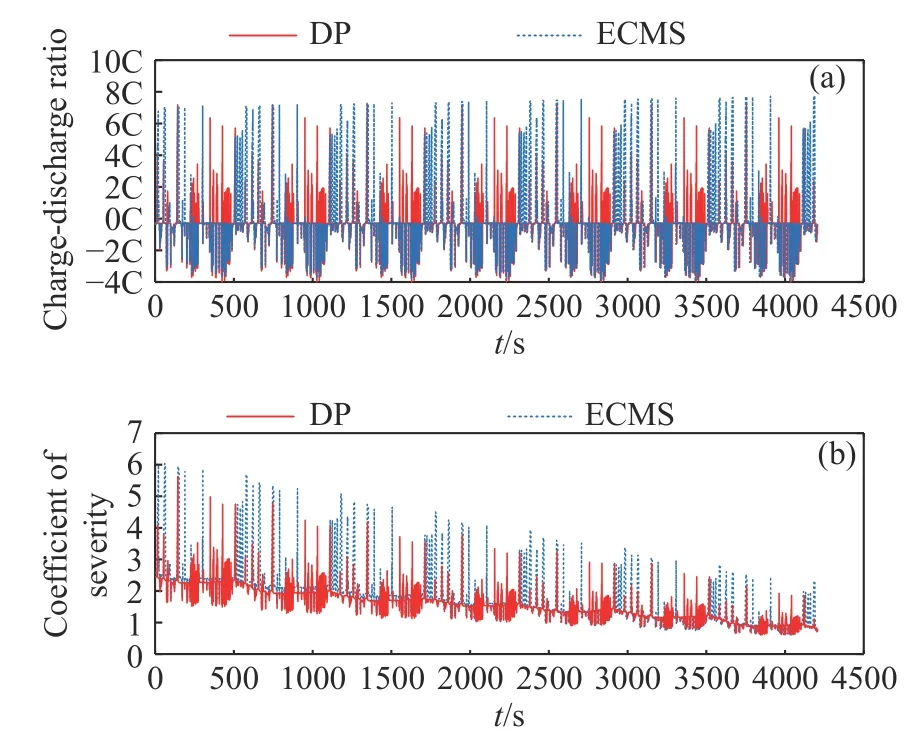
图13 不同方法下的仿真结果对比图.（a）充放电倍率；（b）严重程度系数Fig.13 Comparison figure of simulation results under different methods: (a) charge and discharge ratio;(b) severity coefficient

由图13 可知，相比于DP 结果，在线策略的充放电倍率有一部分要较大，有一部分较小，整体上看还是会稍大于DP 策略的充放电倍率；从严重程度系数上则能够更明显地看出DP 解的系数要小一些，在线策略下的电池老化速度则会稍快一些，两种方法的具体比较结果如表2 所示.图14 为两种方法下的发动机转矩对比及电机转矩对比，由图14 可知，相比于DP 法，在线ECMS 方法的发动机转矩整体要大一些，电机的转矩则要小一些，因而导致车辆的油耗有所增加，这也体现了在线策略无法实现全局最优的一个缺点.

图14 不同方法下的仿真结果对比图.（a）发动机转矩；（b）电机转矩对比Fig.14 Comparison diagram of simulation results under different methods: (a) engine torque;(b) motor torque comparison

由表2 可知，相比于DP 法，在线ECMS 方法的油耗增加了0.82%，有效电量增加了3.7%，所使用的在线ECMS 求解与DP 求解的结果虽存在一定差距，但不论是从油耗还是电池的损耗方面，都在可接受范围内，据此说明了本章所构建的策略的有效性，同时还说明了，在线ECMS 策略方法能够达到接近最优的性能，同时还减少了计算时间，提升了计算速度.

表2 不同方法下的仿真结果对比Table 2 Comparison of simulation results under different methods

4 结论

本文首先对电池性能衰退的主要影响因素进行分析，并搭建了电池的容量衰退模型，据此构建了考虑电池性能衰退的PHEV 控制策略.在此过程中引入了严重程度系数这一概念用来衡量电池的老化程度，通过Pareto 非劣目标域选取合适的权重因子，利用DP 求解，并从电池的充放电倍率、严重程度系数及有效电量Qeff的角度来分析所构建控制策略的有效性.通过验证，其结果表明，在牺牲极小的燃油经济性情况下，可较大地降低电池老化的速度，即较大的降低电池性能衰退；此外，选取一个最优权重系数进行了验证，并与DP优化的方法进行对比，其比较结果表明了所构建策略的有效性.