基于温度效应的半水磷石膏水化反应热动力学模型
王贻明,王志凯✉,吴爱祥,彭青松,李剑秋
1) 北京科技大学土木与资源工程学院,北京 100083
2) 贵州大学化学与化工学院,贵阳 550025
半水磷石膏(Hemihydrate phosphogypsum,HPG)作为一种广泛应用于工程建设的建筑材料,对其生产工艺及化学成分的研究已日趋成熟,但其内部反应机制较为复杂,目前仍无法准确判断HPG胶凝性能的发展趋势[1-3].作为矿山充填胶凝材料,HPG 在堆存状态下会自发地转化为二水磷石膏(Phosphogypsum,PG),胶凝活性下降,难以满足远距离矿山充填所需的力学性能指标要求.要实现HPG 资源化利用技术新突破,关键是阻滞HPG自发地向PG 进行转化,则需对堆存状态下HPG的转化过程进行深入研究.前人研究发现[4-6],胶凝材料的反应活性直接影响水化放热量和放热速率,进而影响硬化浆体的微观结构和力学性能.因此,在堆存过程中HPG 发生化学反应会有水化热的释放,使体系中温度场与化学场相互影响,促进HPG 向PG 转化,故对HPG 水化放热过程进行准确推算、分析和模拟,是有效抑制HPG 转化的前提[7].
为寻求一种模型描述胶凝材料在水化过程中放热量的变化规律,国外学者开展了大量的研究工作.Ulm 和Coussy[8]采用多孔介质理论和热力学方程,探讨了多孔介质热传递理论,并提出一种早龄期混凝土热-化-力耦合模型.Suzuki 等[9]根据混凝土中水分和热量的传导过程,建立了微观粒子水化模型.Gawin 等[10]基于前人研究,提出了混凝土在温度场和化学场耦合作用下水分扩散动力学模型.通过以上研究发现,胶凝材料水化热的释放归根结底是化学反应中能量发生变化,而强度增长源于化学反应过程中反应物的聚合[11-12].
因此,本文基于不同初始堆存温度下HPG 自由水质量分数的变化规律,结合热力学和化学反应动力学基本理论,推导HPG 水化放热演变规律,进而建立HPG 水化反应热动力学模型,并采用COMSOL Multiphysics 软件进行数值验证,该模型可为后期设计延缓HPG 转化方案提供模型指导,对HPG 的推广应用有非常重要的现实意义.
1 不同堆存温度下HPG 自由水质量分数测定试验
1.1 半水磷石膏
试验所用的HPG 选自贵州某化工公司生产车间.HPG 的初始自由水、结晶水质量分数及孔隙率测定结果详见表1.采用国产Winner 2000 型激光粒度分析仪对HPG 进行粒度分析,结果见图1.

表1 HPG 相关性质参数Table 1 Property parameters of HPG

图1 HPG 粒径分布Fig.1 Particle size distribution of HPG
由表1 可知,HPG 初始自由水质量分数较高,达到22.1%,初始结晶水质量分数仅为5.4%,未达到二水石膏理论结晶水质量分数20.93%,表明HPG 具有一定的胶凝活性.HPG 的孔隙度为52.95%,属于土壤孔隙度范畴(43%~54%),则与空气对流热交换系数可近似为20 W·m-2·K-1[13].由图1可知,HPG 由粒径小于100 μm 的颗粒组成,其中颗粒累积分布为10%的粒径D10=20.20 μm,中值粒径D50=57.27 μm,颗粒累积分布为60%的粒径D60=65.29 μm,不均匀系数Cu=3.23,HPG 颗粒级配不良,具有高气孔率,堆存时与空气对流热交换相对较充分.
1.2 不同初始堆存温度控制
试验考虑不同初始堆存温度下HPG 自由水质量分数变化规律,则堆存温度的选择对整个试验及后期现场实际应用非常关键.一般初始堆存温度范围在20~80 ℃区间[14],经过实践检验,发现初始温度降至20 ℃,所耗资超出企业认可范畴,故在此不做进一步研究.35 ℃是HPG 经过多种物理降温措施后,进行堆存时的初始温度,此时经济性较合理;80 ℃是磷酸生产工艺中使用品位较好的矿样制酸时,期间不经过任何物理降温,产生的HPG 初始温度;40 ℃和60 ℃是在生产工艺中经过不同的少许几种物理降温措施产生的HPG 初始温度,因此,本文选取初始堆存温度为35、40、60 和80 ℃进行研究.为保证对HPG 初始温度进行准确控制,对采用不同降温措施的HPG 生产线分别进行跟踪测温、取样,温度误差控制在±2℃,直至选取试验所需温度的试样.值得注意,本次试验的4 组HPG 试样,物料性质存在一定的波动,但相关重要参数无较大差异,不会对试验结果有明显影响.
1.3 堆体制备及温度、自由水质量分数监测
将不同初始温度的试样按照现场堆体形态进行堆筑,放置于温度为25 ℃的恒温养护室(当地年平均温度)进行堆存,此堆筑模型尺寸高为600 mm,底面直径为600 mm.与现场大体积堆体相比,此模型试验只考虑初始堆存温度对HPG 水化放热的影响,暂不考虑尺寸效应[15].
采用温度计对HPG 堆体的表面和中心区域进行监测,了解其温度随时间的变化规律.为准确掌握温度变化规律,规定前1 h 内,以10 min 为周期进行监测,之后每隔1 h 监测一次,直至36 h(矿山经验堆存时间).同时,以3 h 为监测周期,参考《磷石膏》(GB-T 23456—2009)和《石膏化学分析方法》(GB 5484—2000),对HPG 进行自由水质量分数测定,计算方法如式(1)所示.
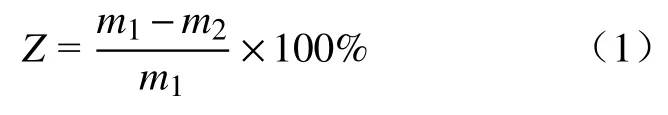
式中:Z为HPG 的自由水质量分数,%;m1为样品烘干前的质量,g;m2为样品烘干至恒重的质量,g.
2 HPG 水化反应热动力学模型建立
2.1 水化反应热力学分析
对HPG 进行热力学分析,首先确定其水化反应的标准吉布斯自由能和标准摩尔生成焓变.参考《高温水溶液热力学数据计算手册》[16],得到CaSO4·2H2O、CaSO4·0.5H2O 和H2O 的热力学数据,见表2.

表2 相关物质热力学数据Table 2 Thermodynamic data for related substances
在25 ℃标准大气压下,HPG 会水化生成二水石膏,其反应方程式为:

式中:Q为水化热.
HPG 水化反应的标准吉布斯自由能为:

HPG 水化反应的标准摩尔生成焓变为:

从热力学分析可以看出,在25 ℃有水坏境中,HPG 水化生成PG 的<0,表明HPG能自发地水化生成PG;<0,说明HPG的水化反应是一个放热过程[17].由此可知,在堆存过程中,随着HPG 自发地水化生成PG,放热量逐渐增大,导致堆体内部温度逐渐升高,加快了水化反应速率,此时体系中的温度场与化学场相互耦合会促使HPG 转化速率加快[18].HPG 在堆存过程中,温度与化学反应相互作用机理如图2 所示,其中,①代表温度对HPG 水化反应的影响,体现在温度对HPG 水化反应速率的影响,使HPG 较早地转化为PG;②代表化学反应对温度的影响,表现为HPG 水化过程中化学反应的热效应(焓变)导致HPG 堆体温度分布发生变化[19].
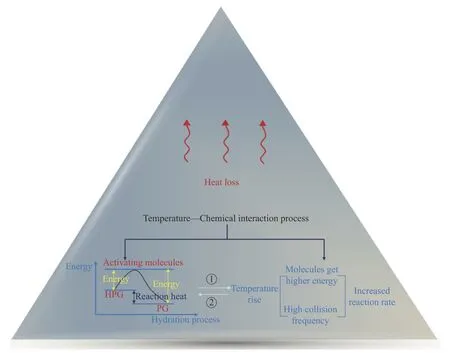
图2 堆体内部温度与化学相互耦合作用关系图Fig.2 Relationship between the temperature and chemical interaction in the reactor
2.2 水化反应的传热方程
2.2.1 传热方程
根据傅里叶热传导定律可知,假设在HPG 堆体内部取一体积元(x,x+dx;y,y+dy;z,z+dz),热流从一面流入,从其他面流出,则净留体积元的热量等于从流入面元减去从其他面元流出的热量[20],如图3 所示.设热流流出为正,则流入体积元的热量dQ为:
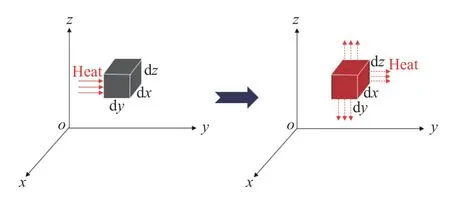
图3 热传导示意图Fig.3 Heat conduction diagram

式中:qx|x+dx、qy|y+dy和qz|z+dz分别为单位时间单位体积x、y和z轴方向流入面元的热量;qx|x、qy|y和qz|z分别为单位时间单位体积x、y和z轴方向流出面元的热量;∇(λ∇T)为体积微元内净留的热量;λ为热传导系数;T为堆存温度.
在HPG 堆体水化放热模型中,可根据广义传热方程(式(4))表达式,推导HPG 水化反应传热方程.在HPG 堆体中没有发生明显流体对流现象,且颗粒之间相互剪切效果也不明显,则流体对流做功放热和黏性放热近似为0;同时,堆体无明显压力做功,则HPG 水化反应传热方程可由式(5)表示.


式中:q为热密度(HPG 水化反应过程某时刻所释放的热量).假定该体系介质为各向同性,则Cp和λ均为常数.
2.2.2 边界条件确定
若堆体内部温度分布用函数T(x,y,z,t)表示,初始条件表达式如式(6)所示.
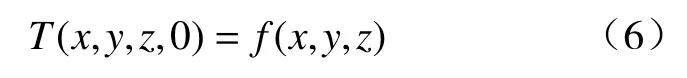
式中,f(x,y,z)为HPG 堆体内初始温度分布情况的函数表达式.
当研究有界区域内的温度分布,边界条件通常有以下三类[21-22].第一类边界条件:若已知区域边界上温度分布,则可归结为第一类边界条件.

式中:∂W为HPG 堆存区域W边界;T1(x,y,z)为∂W上的已知函数.
第二类边界条件:若已知区域边界上每一点的热流密度,由Fourier 定律可知,认为温度沿界面的法向导数是已知的,可归结为第二类边界条件.
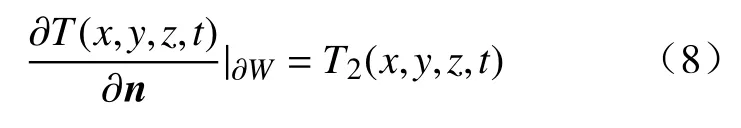
式中:T2(x,y,z,t)为边界上的已知函数;n为∂W的外法线方向的单位向量.
第三类边界条件:若已知周围介质在物体表面的温度为T1(x,y,z,t),在堆存区域表面∂W,HPG和外部介质(空气)间有温差,会产生热量的转移,则满足Newton 热交换定律,在无穷小的时段内,经物体表面无穷小面积流入周围介质中的热量和物体与介质在接触面上的温度差成正比,即:
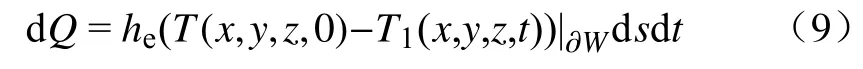
式中:he为热交换系数.
根据HPG 堆存试验发现,模型边界条件可用第三类边界条件表示.由傅里叶定律可知,dt时间内从物体内部流向边界面元ds的体积元热量为:

式(9)与式(10)结合可得:
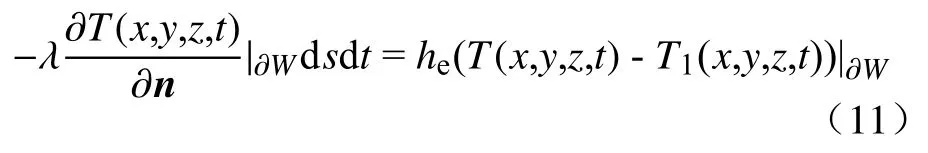
则此体系的边界条件为:

其中:h=>0;T3(x,y,z,t)=为边界上的已知函数;k为反应速率系数.
2.3 水化反应的化学反应动力学方程
HPG 水化过程的化学反应动力学方程可依据体系中自由水质量分数变化规律进行研究,分别对不同初始堆存温度下的自由水质量分数进行数学回归拟合,图4 所示.拟合结果见表3,发现不同堆存温度下HPG 自由水质量分数随时间变化曲线符合一级反应动力学规律[23],且具有较高的相关性.随着初始堆存温度的升高,HPG 自由水质量分数变化幅度增大,反应速率系数增大,表明堆体内部水化反应随温度升高而变得剧烈,体系中的自由水将更快地转化为结晶水.

表3 不同初始堆存温度条件下HPG 自由水质量分数变化规律数学拟合结果Table 3 Mathematical fitting results of the variation law of the HPG free water mass fraction under different initial storage temperatures

图4 不同初始堆存温度下自由水质量分数回归拟合.(a)35 ℃;(b)40 ℃;(c)60 ℃;(d)80 ℃Fig.4 Regression fit of the free water mass fraction at different initial storage temperatures: (a) 35 ℃;(b) 40 ℃;(c) 60 ℃;(d) 80 ℃
对不同初始堆存温度与反应速率系数进行数学拟合,旨在建立一个考虑初始堆存温度和反应速率系数的统一水化反应速率模型.Arrhenius 方程是基于化学反应动力学反映化学反应速率系数随温度变化关系的重要公式[24],故本文采用Arrhenius 方程对HPG 水化反应速率系数与初始堆存温度变化关系的散点图进行指数拟合求解,结果如图5所示.

图5 反应速率常数随初始堆存温度的变化趋势Fig.5 Trends of reaction rate constants with the initial storage temperature
因笔者与文献[25]所用的试验材料均为贵州某化工公司的HPG,其物质的表观活化能不随温度变化而改变,则HPG 的表观活化能为15300 J·mol-1,HPG 水化反应速率方程可由式(13)表示.
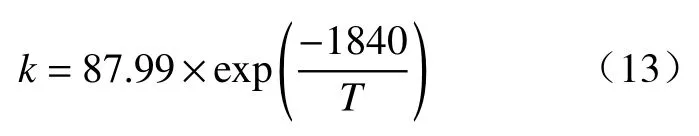
由HPG 水化的标准摩尔生成焓变可知,HPG的水化热为118.28 kJ·kg-1,其热量随HPG 的水化而逐渐释放,则HPG 水化反应过程所释放的热量与其水化率(自由水转化为结晶水的质量分数)密切相关,任意t时刻HPG 堆体水化释放的累积热量Q(t)可表示为:
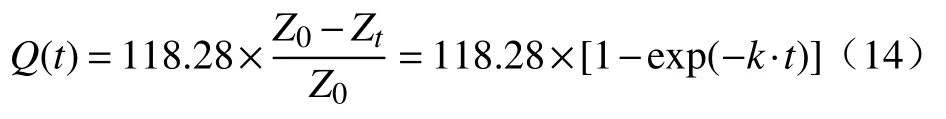
其中:Z0为不同初始堆存温度下的初始时刻自由水质量分数,%;Zt为不同初始堆存温度下堆存时间为t时刻的自由水质量分数,%.
对式(14)求导,则得任意t时刻HPG 水化反应所释放的瞬时热量q(t)为:

式(15)则为HPG 水化过程的化学反应动力学方程.
根据HPG 水化反应传热方程和化学反应动力学方程的结果,将式(5)与式(15)整理,并结合式(13),可得HPG 水化过程中温度-化学耦合作用模型,即HPG 水化反应热动力学方程,具体表达式为:

需要注意的是,式(16)中的具体表达式可能会因温度、试验材料和堆体体积等不同而产生差异,但是其温度-化学耦合形式可供其他胶凝材料参考.
3 HPG 水化反应热动力学数值模拟
3.1 物理模型及网格划分
由于室内堆存实验的堆体为圆锥体(高度为600 mm,底面直径为600 mm),可采用二维轴对称几何模型进行模型构建,二维轴对称模型可以节省运算时间且不会影响模拟结果[26].之后对几何模型进行映射网格划分,此次数值模拟考虑到堆体与空气之间存在对流热交换,故对模型边界处的网格进行细化,以保证边界热交换计算结果更为准确.对称物理模型及其网格划分,如图6 所示.

图6 对称物理模型及网格划分Fig.6 Symmetric physical model and grid division
3.2 传热与常微分方程(ODE)模块
采用COMSOL 软件对HPG 水化反应热动力学方程进行求解,需在软件中选取传热模块与数学模块进行耦合模拟计算.对多孔介质传热模块中内嵌的方程进行设置,并辅以ODE 模块,将完整的本构方程进行嵌入并计算,该模型嵌入过程如图7 所示,材料相关属性见表4.

表4 相关参数设置Table 4 Relevant parameter settings

图7 本构模型嵌入.(a) 传热模块设置;(b) ODE 模块设置Fig.7 Constitutive model embedding: (a) heat transfer module setup;(b) ODE module setup
3.3 模拟结果
图8 为模拟堆体温度变化结果与试验结果数据对比图.对比结果可以看出,模拟内部温度变化结果与试验数据基本吻合,说明本文建立的HPG水化反应热动力学本构模型是可靠的,但是模拟表面温度结果相比实测试验数据要低,推测是由于监测外表面温度时,温度计插入堆体外表面层,导致模拟温度低于实测温度.

图8 模拟温度变化曲线与试验结果对比.(a) 内部温度;(b) 表面温度Fig.8 Comparison of the simulated temperature change curve with the test results: (a) internal temperature;(b) surface temperature
不同初始温度下HPG 堆体的内部温度均经历升温、快速冷却、缓慢冷却三个阶段.其中堆体内部温度在前10 min 内均在升高,升高范围在0~1 ℃,原因是:在堆存前期,HPG 反应较剧烈,水化产生的热量无法及时散发,水化放热速率大于对流散热速率,则内部温度呈逐渐升高.快速冷却阶段是因为水化放热速率下降,使反应产生的热量可通过对流散热方式得到快速释放.值得注意,在快速冷却阶段中,不同初始温度的堆体持续时间不同,其中80 和60 ℃的堆体在8 h 后,进入缓慢冷却阶段,40 ℃的堆体在11 h 后进入,35 ℃的堆体在9 h后进入.推测初始温度为80 ℃和60 ℃的堆体在快速冷却阶段持续时间较短,是因为初始温度较高,导致内部HPG 水化反应速率增大,促使HPG较早地转化为PG,使后期没有反应热源提供热量;而初始温度为35 ℃的堆体,在快速冷却阶段仅持续至9 h,推测是由于内部温度较低,仅有部分HPG 发生反应,产生少量的热能较早地被对流散发.经过快速冷却阶段之后,堆体中大部分的HPG 已经反应生成PG,放热速率开始降低,内部温度也逐渐下降,直至最后温度保持恒定.不同初始温度下HPG 堆体表面温度呈逐渐下降趋势,原因是堆体表面与空气直接形成热对流,使其快速发生热交换,直至后期表面温度趋近于环境温度而不发生变化.
图9 为不同初始温度的堆体在堆存36 h 时的温度云图.根据模拟结果可知,堆存36 h 时,堆体内部温度均有不同程度下降,但不同堆体的内部温度随着初始温度增加而增加,堆体表面温度均趋近于环境温度.综上所述,建议HPG 堆体初始温度尽量控制在40 ℃以下,即可以保证在长时间堆存状态下HPG 保持较好的胶凝性能,又能保证降温费用的经济合理,有利于HPG 的资源化利用.

图9 不同初始堆存温度HPG 堆体堆存36 h 后温度云图.(a) 35 ℃;(b) 40 ℃;(c) 60 ℃;(d) 80 ℃Fig.9 Temperature cloud diagram after storage of 36 h HPG with different initial storage temperatures: (a) 35 ℃;(b) 40 ℃;(c) 60 ℃;(d) 80 ℃
4 结论
(1)通过热力学分析,发现HPG 在堆存过程中能自发地水化生成PG,而且HPG 的水化反应是一个放热过程.随着水化反应的进行,放热量逐渐增大,堆体内部温度逐渐升高,加快了水化反应速率,使堆体中温度场与化学场相互作用,促使HPG快速转化.
(2)基于热力学及化学反应动力学的基本理论,结合自由水质量分数变化规律,提出堆存温度与时间关系的HPG 水化反应热动力学本构模型.采用COMSOL 数值模拟软件,将本构模型嵌入传热和ODE 模块,对不同初始堆存温度的堆体进行数值模拟,模拟温度变化曲线与实测结果较为吻合,验证了本文所提出HPG 水化反应热动力学方程的可靠性.
(3)通过对不同初始温度下HPG 堆体内部温度变化分析,建议HPG 堆体初始温度尽量控制在40 ℃以下,即可以保证在长时间堆存下HPG 有较好的胶凝性能,又能保证降温费用的经济合理,有利于HPG 的资源化利用.
(4)对于散热条件较差而导致内部热量无法散发的大体积HPG 堆体,体系内部水化过程可能与本文构建的模型存在显著的差异,需在后续研究中,针对大体积HPG 堆体开展深入研究.

