链段刚性对非溶剂致相分离成膜过程影响的耗散粒子动力学模拟

唐元晖，李春玉，林亚凯，张春晖，刘泽，余立新，王海辉，王晓琳

（1.中国矿业大学(北京)化学与环境工程学院,北京 100083；2.清华大学化学工程系,膜科学与工程北京市重点实验室,北京 100084）

近年来，以膜作为分离过程核心组件的膜分离技术在海水淡化、工业废水及生活污水处理等水处理领域得到越来越广泛的应用.非溶剂致相分离（NIPS）法，通常也称为浸没沉淀法，是20世纪60年代就被提出的多孔膜制备方法，其过程是在常温下将聚合物溶液浸没在聚合物的非溶剂（凝固浴）中，使聚合物溶液内的溶剂与非溶剂发生跨界面的双扩散传质过程，诱导聚合物溶液相分离并形成非对称膜结构.通过NIPS法制备的聚合物膜，微观上通常是由疏松通透的多孔断面主体和致密聚合物表层组成的非对称结构，是目前应用最广泛的超滤/微滤膜材料［1］.其中，非溶剂与溶剂间传质诱导的相分离对最终聚合物的孔隙率、孔径分布等膜的微观结构特征以及膜的强度和渗透性等性能有着决定性的作用［2］.目前对NIPS过程得到的膜结构的优化和膜性能的提升主要依赖于实验的反复尝试，缺乏对相分离过程本身复杂的热力学和动力学因素的深入理解.为了更好地掌握操作参数与膜微观结构之间的联系，从20世纪80年代开始，Wang等［3］采用模型和模拟的方法来描述和研究NIPS过程，多数是基于Flory-Huggins热力学理论和传递过程原理来对膜形成过程中的浓度场和温度场进行数值分析，并结合体系热力学相图得到系统在相分离中的相变路径从而实现对膜结构的预测［4］.不过传质计算无法直观地展示相分离过程和膜微观结构特征.近20年来，随着高性能计算在硬件和软件上的快速发展，推动了计算机模拟方法，包括分子动力学（MD）、蒙特卡洛（MC）及耗散粒子动力学（DPD）等，在流体相分离和流动领域的广泛应用，使得可以基于分子或者粒子体系和合适的相互作用力场，直接模拟聚合物溶液的相分离过程.

DPD是1992年由荷兰的Hoogerbrugge和Koelma在分子动力学模拟的基础上提出、1997年由英国的Groot和Warren完善的一种基于粗粒化分子的流体动力学模拟方法［5］.由于其模拟体系的时空尺度能达到微米和毫秒的介观尺度［4］，自提出后就受到了复杂流体动力学领域研究者的关注，在聚合物体系相分离［5，6］、表面活性剂［7］及微通道流动［8］等领域均有广泛应用.近年来，DPD也逐渐被用于研究聚合物溶液体系的NIPS动力学过程和相应的成膜机理中.

2008年，Lu等［9］率先使用DPD构建了虚拟聚合物体系的二维模型来模拟NIPS过程.2018年，本课题组［10］针对NIPS法聚合物/溶剂/非溶剂体系的成膜过程的早期阶段构建了DPD三维模型，得到了体系相分离形貌演变及相区尺寸变化等重要结果，说明DPD能够成功应用于聚合物溶液的NIPS过程的动力学研究.本课题组［11］针对聚醚砜（PES）/N-甲基-2-吡咯烷酮（NMP）/水的实际体系，研究了NMP和水的跨界面传质和聚合物浓度等对PES相分离早期过程和膜孔径结构的影响.

在上述模拟NIPS过程的研究中，均采用了Groot和Warren在1997年提出的弹簧力来链接聚合物相邻的重复单元［5］，其中弹簧力（）的表达式如下：

式中：K为弹簧常数，K=4；为聚合物相邻重复单元间的距离，DPD模拟中涉及的单位通常按照一定的规则归一化使用无因次量纲［5］，因此本文中DPD力场相关物理量的单位按照引用文献的规则归一化为1.

在此力场中聚合单元间仅存在距离限制，而缺少角度等限制，导致弹簧力场控制下的聚合物链段是很柔软的.

目前常用的有机膜原料按聚合物链段柔性可分为柔性聚合物（如聚偏氟乙烯及聚丙烯等）和刚性聚合物（如聚砜和聚醚砜等），弹簧力场则主要适用于链接柔性聚合物的重复单元.由图1可见，PES链段中相邻重复单元存在空间位阻较大的砜基和苯基结构，这意味着结构单元间的角度是无法随意弯曲的，呈现出一定的刚性.然而弹簧力场控制下的PES链段是很柔软的［式（1）］，同时Dingeman等［12，13］研究发现，描述聚合物链段的力场会影响聚合物链段的径向分布函数，进而可能改变聚合物的相行为.

Fig.1 Atomic structure of PES(A)and schematics of the MD simulation strategy for the PES/NMP solution formation process(B)

为了更加准确地模拟PES/NMP/水体系的NIPS过程并考察PES刚性对相分离过程的影响，本文基于量子力学计算构建了PES/NMP溶液，通过对PES单体间距离和角度分布映射的方法将分子动力学模拟所得的原子尺度信息与DPD粒子间的相互作用联系起来，构建了符合PES链段刚性的简谐力场；然后在前期已构建的PES/NMP/水体系的DPD模拟平台基础上［11］，对比简谐力场与式（1）的弹簧力场对聚醚砜溶剂相分离过程的影响，并考察了不同聚合物浓度下该体系相分离的变化，最后结合文献中的实验结果得到综合评价.

1 模拟方法及模型构建

1.1 模拟方法

分子动力学是一种基于牛顿力学来模拟由原子构成的分子体系的动态行为或宏观性质的方法.在分子动力学模拟中，原子和分子间的相互作用分为成键相互作用（如键长势能、键角势能等）和非键相互作用（如范德华相互作用、氢键等）.通常将这些相互作用以数学形式的力场进行表达，常用的力场有GAFF力场［14］、AMBER力场［15］及CHARMM力场［16］等.本文根据量子力学采用Gaussian软件［17］构建PES/NMP溶液的全原子体系，使用Amber软件［18～21］开展PES溶液的MD模拟，选择的力场是GAFF.由于本文的重点在于MD与DPD之间的映射和DPD模拟，关于MD的模拟细节请参考文献［22，23］.

DPD是一种粗粒化的分子动力学，该方法将微观粒子粗粒化为一定量原子或分子的集合.为了便于运算，DPD模拟通常采用约化单位［5］，即用于描述DPD力场的物理量的单位均为1.在DPD体系中，每个粒子具有相同的质量，粒子质量中心的运动符合牛顿运动方程，且所有的DPD粒子都会受到3种力的作用［24］：保守力（FC）、耗散力（FD）和随机力（FR），它们都是粒子对间在截断半径（rc）距离内的相互作用，其中保守力是用于表征体系特性的力，其表达式如下：

式中：αij为粒子间的排斥力参数；耗散力体现了体系黏度，随机力反映了热涨落的影响，表达式分别为：

式中：ωD和ωR是依赖于r的权重函数，并且当rij＞rc时其值均为是一个符合高斯正态分布的随机变量；参数γ和σ分别是耗散力和随机力的系数.耗散力和随机力也是作用于两个粒子质心的连线，同时保证动量守恒，耗散力使体系粒子的温度降低，随机力给体系注入能量，耗散力和随机力分别起到了摩擦作用和噪声作用，两者结合起来成为一个热浴.

1.2 MD到DPD的映射

为了构建更加准确的DPD力场来描述聚合物链段，近年来研究者们开展了很多研究来更精准地构建从全原子到DPD粒子体系的粗粒化映射.Lu等［25］从MD模拟中获得聚乙烯链段的径向分布函数，进而得到聚乙烯重复单元间的距离和角度分布，而后在DPD体系中依据距离和角度分布以及Rosenbluth规则进行原子再生长，从而得到结构更加合理的聚乙烯链段；Ortiz等［26］从MD模拟中获得了环氧乙烷-聚乙二烯（PEO-PEE）嵌段共聚物的均方根偏差（RMSD），而后将RMSD映射到DPD体系，进而得到了符合PEO-PEE嵌段共聚物结构特征的力场.根据上述研究结果，本文将通过MD模拟获取PES单体质心间距离和角度的分布，并将其映射到DPD体系，从而构建符合PES链段刚性的简谐力场.

1.2.1 MD体系构建 通过MD对PES/NMP在室温下形成的溶液开展模拟，得到热力学平衡态，从而获得PES链段在NMP中PES重复单元间的距离和角度的平衡分布结构特征.为了构建PES/NMP的全原子体系，本文基于量子化学方法，使用Gaussian软件构建PES单体以及NMP分子并对其进行优化，其中结构优化时选择了MP2方法，基组为6-31g（d），静电荷优化时采用Merz-Kollman方法得到了拟合静电势电荷.基于此优化的结构采用Amber软件构建出聚合度为30的PES链，并在真空中进行能量极小化和分子动力学平衡，从而得到结构合理且松弛的PES聚合物链段.最后利用Packmol软件［27］构建聚合物质量分数为16%的PES/NMP溶液盒子，盒子采用周期性边界条件，由于MD体系时空尺度的限制，将溶液设置为仅含有5条重复单元数为30的PES链，溶液构建过程如图1所示，即将PES链和一定数量的NMP分子放入模拟盒子中，通过Amber软件进行能量极小化和分子动力学过程，并在温度为298 K条件下运行100 ns的NPT系综以保证体系达到稳定状态，从而得到稳定的PES/NMP溶液，最终该体系总能量、温度、压力及密度均达到稳定状态（图2）.

Fig.2 Evolutions of the density and pressure(A),energy and temperature(B)of PES/NMP solution in the NPT ensemble during 100 ns

本文中分子动力学过程所采用的力场为Amber中的GAFF力场，其表达式如下［14］：

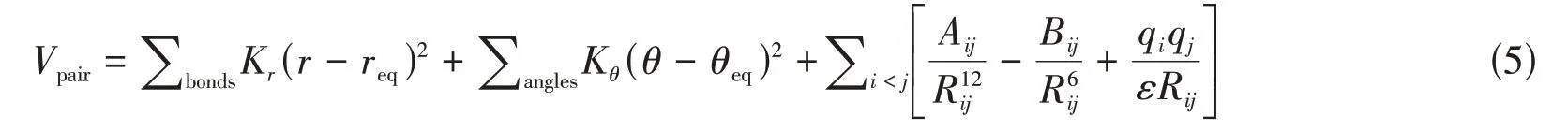
式中：Vpair为体系总势能；r和θ分别为粒子间距离和角度；req和θeq分别为平衡距离和平衡角度；Kr和Kθ分别为键势能常数和角势能常数；Rij为粒子i和粒子j质心间的距离；Aij，Bij和ε均为势能参数；qi和qj分别为粒子i和粒子j所带电荷数.由式（5）可以看出，GAFF力场主要由键长相互作用、键角相互作用以及非键相互作用三部分组成.

1.2.2 DPD体系构建 从图3（A）可以发现，PES单体或NMP分子整体呈平面结构，与DPD粒子的球形结构偏离较大，但从参考文献［5，7，26］等中均可以发现，将分子粗粒化为DPD粒子并没有严格遵循分子本身的结构，而是根据模拟体系本身的物性确定的粗粒化方案.因此，本文基于本课题组已发表的工作［11］，将PES单体和NMP分子的实际体积映射到DPD模型中：分别将1个PES单体或2个NMP分子粗粒化为1个DPD粒子，1个DPD粒子所占据的体积为0.2 nm3.其映射模型分别如图3（A）所示.在DPD模拟中，长度单位为截断半径（rc′，nm），质量单位为粒子质量（m′，g/mol），能量单位为［（kBT）′，J］（上标′为模拟中带单位的量）.为了便于计算，通常对各个单位进行无量纲化处理［5］，由此得到长度单位为rc，质量单位为m，能量单位为kBT.本文中每个DPD粒子所占据的体积均为0.2 nm3，数密度为3，即单位体积的空间区域可容纳3个粒子，进而得到时间单位为τ′=其中玻尔兹曼常数kB=1.38×10-23J/K，参考温度Tref=298 K，M是所有粒子的平均分子量，根据本课题组之前的研究结果［11］，本文中M=203，所以时间单位τ′=7.9×10-12s，并且在DPD模拟中所使用的时间步长Δt=0.01τ′.

在粗粒化模型和时空尺度确定后，开始构建PES/NMP溶液的DPD模型体系.PES链的聚合度与MD体系均为30，溶液的聚合物质量分数也均为16%，由于后续模拟相分离过程需要用水作为凝固浴，而NMP的黏度大于水，为了将两者黏度进行区分，本文将NMP模型设置为两个DPD粒子相连，而水模型为单独的DPD粒子（图3）.然后采用GALAMOST软件［28］构建尺寸为20rc×20rc×20rc的聚合物溶液盒子，盒子采用周期性边界条件.然后在298 K条件下，对溶液进行30000τ的均一化［图3（B）］.

Fig.3 Schematics of the coarse-graining from the molecular level to the DPD particles(A)and a snapshot of the DPD equilibrium system of the PES/NMP solution(B)

在PES/NMP溶液的DPD体系中，粒子间的相互作用通过排斥参数αij实现，而排斥参数αij与Flory-Huggins相互作用参数χij有关，其关系式如下：

式中：当温度为298K时，kBT=1，相同粒子间的排斥参数αij=75kBT/ρ=25［5］.PES与NMP间的相互作用参数χij=0.16，排斥参数αij=25.56.

此外，对于构成PES链的粒子之间的相互作用方式，本文引入了简谐键势能（Harmonic bond potential）和简谐角势能（Harmonic angle potential），从而取代Warren所提出的弹簧势能，其中简谐键势能［Vbond(r)］表达式为［28］：

式中：kb表示弹簧常数；rb表示平衡距离.

简谐角势能［Vangle(θ)］表达式为［28］：

式中：ka表示势能常数；θa表示平衡角度.

1.2.3 MD到DPD的映射通过映射的方法将MD模拟所得的原子尺度信息与DPD粒子间的相互作用联系起来，具体方法如图4所示.首先利用Amber中的cpptraj模块对MD体系中PES相邻重复单元的质心间的距离和角度分布数据进行统计及高斯拟合，得到的PES相邻重复单元间的距离和角度示意图如图4（A）所示；然后在DPD体系中，通过预估简谐力场中［即式（7）和式（8）］的参数kb，rb，ka和θa，并按1.2.2节的方法得到均一稳定的PES/NMP溶液，对构成PES相邻粒子质心间的距离和角度分布数据进行统计和高斯拟合，这些距离和角度可以近似地理解为DPD粒子间的键长和键角；接下来将拟合得到的均值和方差与分子动力学所得结果对比，不断调整简谐力场参数，并重复上述步骤，直到DPD体系所得的键长和键角分布与MD体系趋于一致［图4（B）］，即在该力场参数条件下DPD体系的PES结构最接近于MD体系.最终拟合得到的两体系的均值和方差如表1所示，键长和键角分布高斯曲线如图5（A）和（B）所示，本文所构建的DPD简谐力场表达式为：

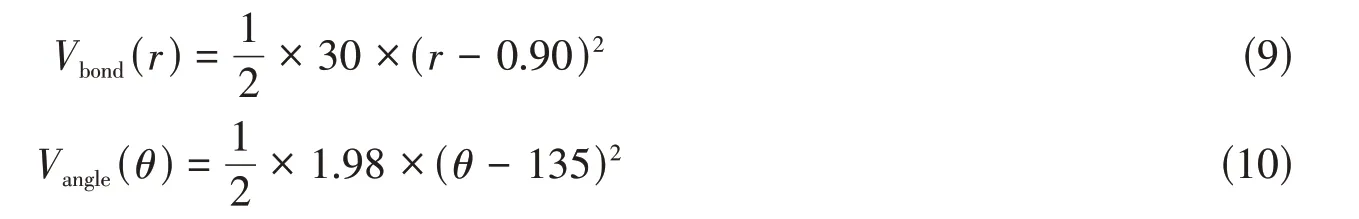
Fig.4 Schematic diagram of the mapping of bond length and angle from MD(A)to DPD(B)

Table 1 Mean and variance of bond lengths and angles in MD and DPD simulation

此外，由表1和图5可以发现，DPD体系的键角分布均值和方差与MD体系基本一致，这说明对于聚合物链键角的优化效果是较好的.虽然DPD体系的键长分布的均值与MD体系基本一致，但两者分布的方差间差距较大，这是因为在DPD体系中，键长方差的大小取决于简谐键势能表达式中参数kb的大小，kb越大，方差越小.但我们并没有过度提高kb的值，否则会使简谐力场的刚性过强，降低模拟效率：导致DPD需要更小的步长来避免体系发生可能的崩溃，降低DPD体系可达到的时空尺度.

Fig.5 Distribution of bond length(A)and angle(B)between consecutive PES repeat units

1.3 DPD模型构建和模拟结果表征

采用与1.2.2节相同的方法得到PES/NMP/水体系的粗粒化模型，最终该体系的粗粒化参数如表2所示，粗粒化模型如图6所示，粒子间的相互作用参数χij及排斥参数αij如表3所示.

Table 2 Molecular volume,molar mass,and the number of species per particle for PES,NMP and water

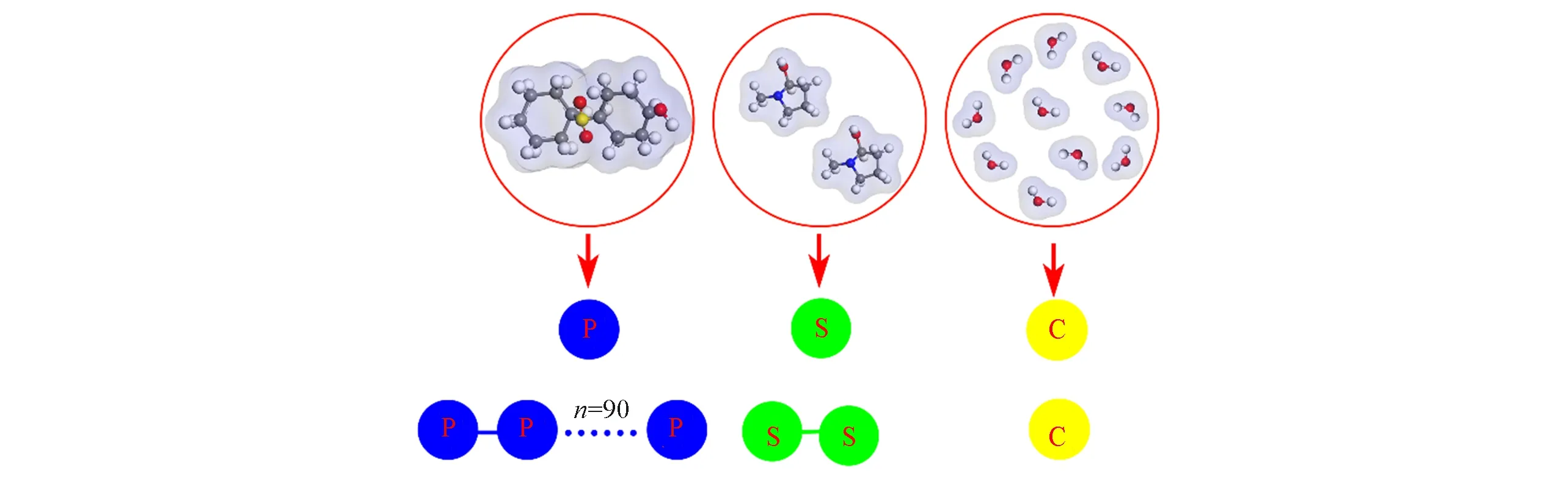
Fig.6 Schematics of the coarse-graining from the molecular level to the DPD particles

Table 3 Flory-Huggins interaction parameter χij and the corresponding DPD repulsio n parameter aij between different species

在DPD模拟阶段，本文分别构建凝固浴盒子（尺寸为90rc×50rc×90rc）和聚合物盒子（尺寸为90rc×90rc×90rc），并且两盒子在x和z方向均为周期性边界条件，y方向设置了中性基板限制.中性基板是由两层冻结的DPD粒子构成的，并且近基板区域设置了反弹边界条件，本文中的中性基板与聚合物、溶剂的相互作用参数均等于10.8，该值已在文献［5］中被证明能正确描述体系在边界处的密度分布.

分别对聚合物和凝固浴进行30000τ的均一化，以确保粒子均匀分布在各自的空间内.将平衡后的两体系按照图7（A）所示的方式拼接在一起，并移除两体系中间部分的中性基板［如图7（A）中的箭头所示］，此时该体系的尺寸为90rc×140rc×90rc.图7（B）显示了初始状态下PES浓度为12%（体积分数）时各个粒子的体积分数分布以及总粒子数密度分布.值得注意的是，体系的总粒子数密度在y=50rc处略有降低［图7（B）洋红色虚线由3.0降至2.8］，这是移除两体系中间部分的中性基板导致的，但总粒子数密度的变化幅度较小，因而其对整体的影响可以忽略.将聚合物溶液与凝固浴间的临时壁移除后，使PES溶液与非溶剂（水）充分接触混合，并对相分离过程进行10000τ的DPD模拟.

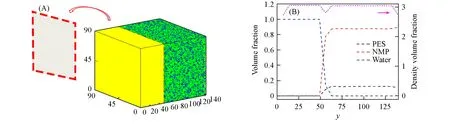
Fig.7 Schematics of the DPD simulation strategy for the membrane formation process via NIPS

采用与前期工作［11］相同的表征方法对DPD模拟结果进行表征.首先采用回转半径（Rg）对PES链段刚性进行表征，其计算方法如下：

式中：ri是链段i的位置；rcm是聚合物链质心的位置.由式（11）可知聚合物链段刚性越强，其重复单元距离链段质心间的距离越大，进而导致其均方回转半径越大.

相分离过程的形貌表征是通过程序计算得到体系中不同区域的密度分布，并基于Matlab软件绘制了局部聚合物体积分数大于或等于45%的等值面.本文中DPD体系数密度为3，而模拟的聚合物溶液的体积分数为8%～16%，均小于33%，这意味着聚合物溶液均一时单位体积的空间区域内存在0～1个聚合物粒子，当聚合物溶液发生相分离时，聚合物富相区域单位体积空间内可聚集2～3个聚合物粒子，因此通常认为局部聚合物体积分数达到40%～50%即为富相区域.本文选择局部聚合物体积分数45%作为聚合物富相与贫相的临界点，前期工作中［11］同样采用的是该值.由于体系中存在跨越相界面的粒子传递，必然会造成体系中沿流动方向（即y轴）上的局部密度发生明显的变化，本文计算了各个粒子沿y轴方向的密度分布以及每个区域内的平均粒子数.聚合物的相区尺寸是公认的相分离过程的常规表征手段，本文采用与前期工作［11］相同的计算方法，有别于常规均匀体系的相区尺寸计算［29］，本文的相区尺寸去除了如图7（A）所示的凝固浴部分，仅计算了铸膜液一侧的聚合物相区尺寸随时间的变化.

除了相分离过程的表征，本文以相分离形貌较完善的体系认定为可能形成的膜结构，计算了此时模拟所得聚合物膜的二维和三维孔径分布，其中二维孔径的计算方法为：首先通过程序计算了体系中不同局部区域的密度场体系的密度场，然后沿y轴扫描，对于xz二维截面中PES粒子体积分数小于45%的区域（聚合物贫相区域）即认定为孔径区域，通过统计沿y轴孔径区域所占的面积即得到了聚合物膜的二维孔径分布，这种二维孔径分布可以直接地反映体系沿粒子传质方向上体系的不对称性变化；对于三维孔径的获取，首先去除了凝固浴所在部分的区域，而后使用Zeo++软件进行分析［30］.

2 结果与讨论

首先在聚合物体积分数为12%的条件下，探究聚合物链段刚性对PES/NMP/水体系相分离过程的影响；然后在简谐力场条件下，探究聚合物体积分数从8%增加至16%时PES/NMP/水体系相分离过程的变化.

2.1 聚合物链段刚性对NIPS法成膜过程的影响

将PES链长设定为90，聚合物初始体积分数为12%，对比了两种力场条件下体系相分离过程随时间的变化.图8为在4个时间步长（2500τ，5000τ，7500τ和10000τ）下的相分离形貌图，其中蓝色区域为局部聚合物体积分数大于或等于45%的等值面.在PES/NMP溶液与水之间的界面上，水和NMP快速进行物质交换，导致聚合物在界面区域快速聚集，形成薄而致密的聚合物表层.从图8可以观察到，简谐力场的成膜速度更快，并且形成的膜也更加致密，在2500τ时［图8（A）］已初步形成了聚合物表层.随着聚合物表层的逐渐形成，界面处的NMP与水的交换速率逐渐变慢，并且由于非溶剂水的推动，聚合物表层逐渐向盒子的右侧移动，并且随着时间的推移，水逐渐扩散到溶液内部区域，聚合物层逐渐生长，且变得更加致密.同时PES溶液内部逐渐发生聚合物聚结，由此产生了表层下的多孔亚层结构，这是典型的聚合物富相成核和生长的特点.

为了更加直观地描述以上现象，并探究力场对膜结构的影响，计算了体系中各粒子沿y轴的体积分数分布以及总数密度分布（图9），图9中洋红色虚线表明该体系是总数密度为3的粒子均匀分布体系，这与DPD初始设置的条件相吻合；通过比较同一力场的不同时刻NMP和水的粒子分布（图9中红色和蓝色虚线）可以发现，初始时水位于凝固浴侧，NMP位于铸膜液一侧，随着时间的推移两者逐渐相互扩散，并且在PES体积分数分布（图9中黑色虚线）的峰值处两者的扩散趋势明显减缓，这是由于在界面附近形成了致密的聚合物层导致的.

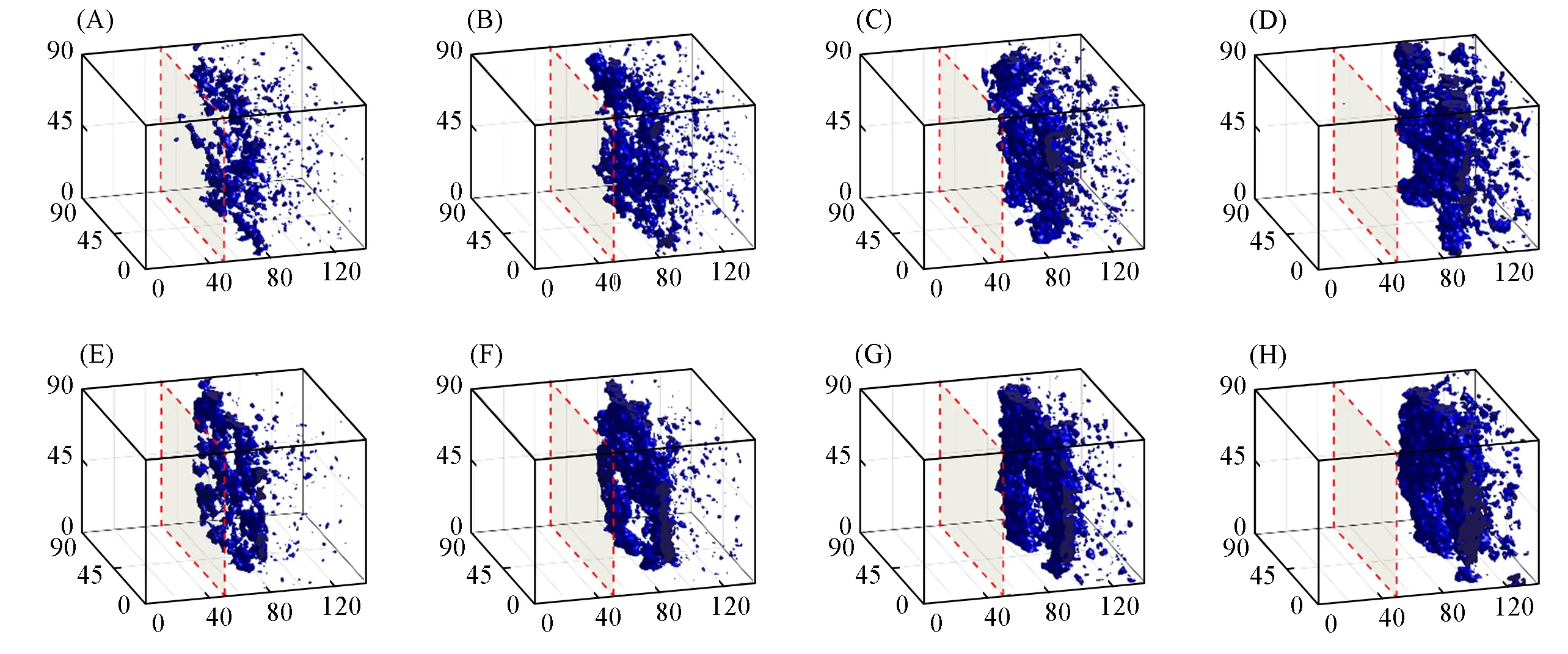
Fig.8 Morphology evolution of the systems with initial polymer volume fractions 12% in spring force field(A—D)and harmonic force field(E—H)at 2500τ(A,E),5000τ(B,F),7500τ(C,G)and 10000τ(D,H)during the DPD simulations

Fig.9 Profiles of volume fraction of PES(black),NMP(red)and H2O(blue)and total particle density(magenta)along the y axis in spring force field(A—D)and harmonic force field(E—H)at 2500τ(A,E),5000τ(B,F),7500τ(C,G)and 10000τ(D,H)during the DPD simulations

图10给出不同力场下PES在不同时刻的体积分数分布.初始的PES浓度在溶液侧的分布是均匀的，由于非溶剂水和溶剂NMP在界面上的传质，使得PES在相界面上逐渐形成了致密层，正好对应于PES体积分数上的峰值，此峰的高度逐渐增加并且向右移动，且其峰宽度保持相对恒定，进一步说明了PES表层的厚度不变但更为致密.在两种力场条件下，聚合物形态随时间变化（图8）以及聚合物体积分数分布演变（图10）非常相似，这说明两者相分离机制是相似的.尽管在两种力场条件下都能观察到相似的行为，但是各组分的体积分数变化速率存在明显的差异，简谐力场条件下的NMP和水的传质速率以及成膜速度更快.此外，简谐力场中PES峰明显高于弹簧力场，但是峰宽却略小于弹簧力场，这表明简谐力场形成的膜表层更加致密且略薄.

图11（A）给出不同力场条件下Rg随时间的变化.首先，随时间的延长，Rg值迅速减小，简谐力场从6.59rc降至6.14rc，弹簧力场从6.59rc降至3.99rc，在1500τ后减小趋势变得非常缓慢.这可能是因为初始时NMP与水发生快速的物质交换，导致界面处聚合物快速析出，因而Rg迅速降低；随后由于膜表层的形成，导致NMP和水传质速率降低，聚合物析出速率同样降低，所以Rg减小趋势也逐渐平缓.此外，还发现简谐力场的Rg值始终大于弹簧力场，这说明弹簧力场下的PES链段更柔软，而简谐力场在其基础上增加了对聚合物结构单元间键角的约束，使聚合物刚性更大，这与文献［31］中的结论一致.

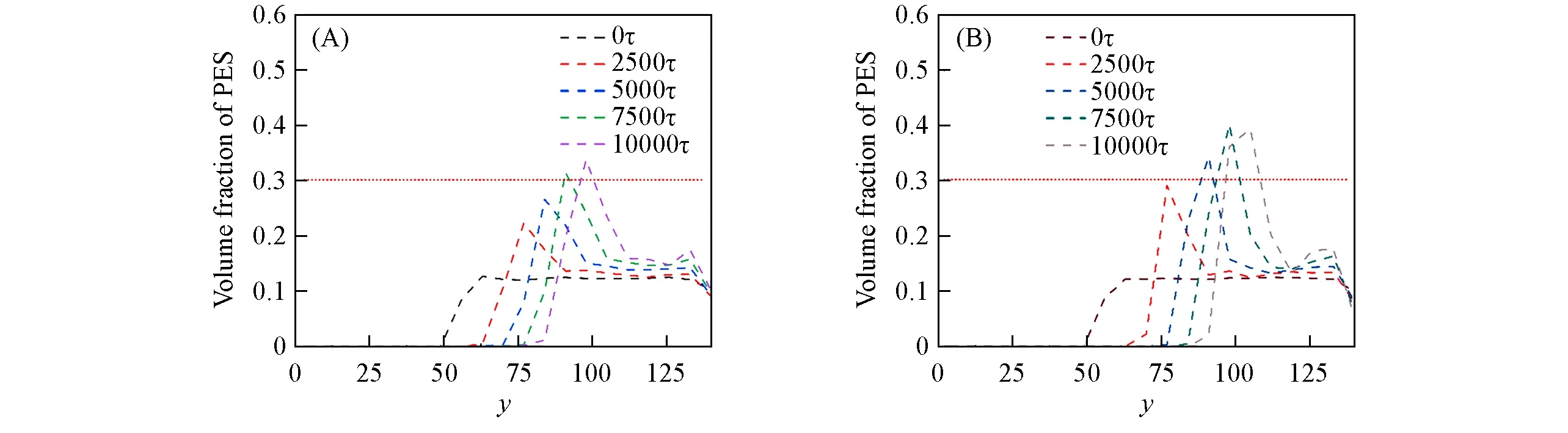
Fig.10 Profiles of volume fractions of PES along the y axis at spring force field(A)and harmonic force field(B)of different times

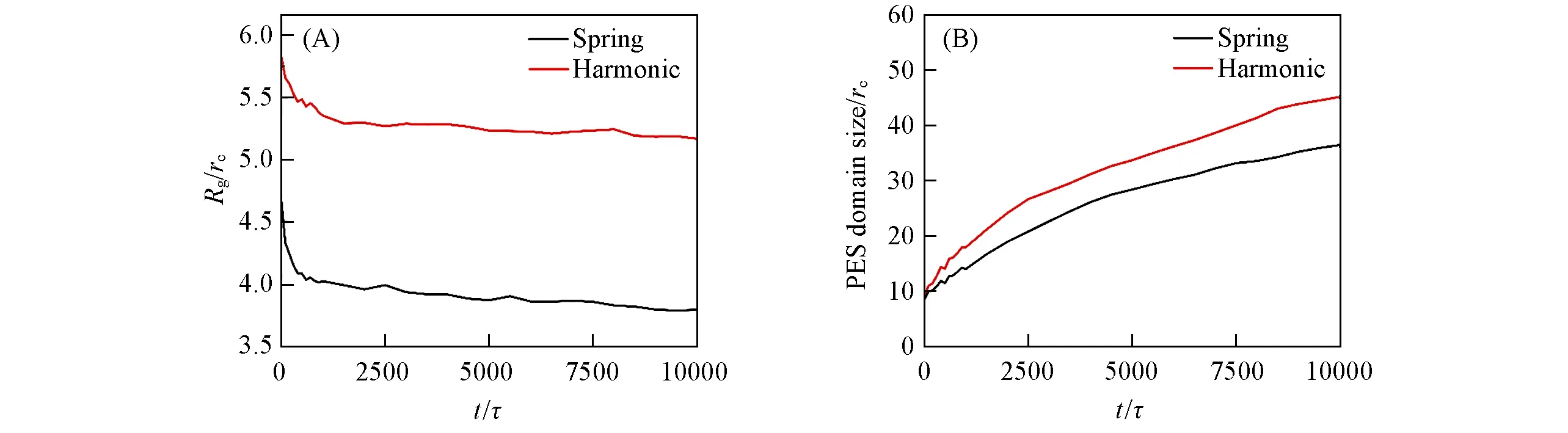
Fig.11 Evolution of radius of gyration Rg(A)and PES domain size(B)as functions of time for the systems in harmonic force field and spring force field

聚合物的相区尺寸变化是衡量聚合物体系相分离程度的常用手段，相区尺寸增大表明从铸膜液中析出的聚合物富相在逐渐增长，即相分离的程度增大.图11（B）给出PES的相区尺寸随时间变化.可见，随着相分离的进行，相区尺寸先快速增长，而后缓慢增加.初始时增加较快可能是由界面处聚合物迅速成膜引起的，随后成膜速度降低，导致相区尺寸增长也趋于平缓.此外，在整个过程中，简谐力场的相区尺寸一直大于弹簧力场，这也进一步印证了简谐力场条件下聚合物刚性较大，链段不容易被压缩这一结论.

对于不对称的形态结构，二维（2D）孔径分布和三维（3D）孔径分布都是有重要意义的.二维孔径表示在二维截面中孔径区域所占面积的大小，其可以间接地反映孔隙间相互连通的程度；而三维孔径分布表示的是整体孔径大小的分布，其与膜的渗透性有直接关系.由图10可见，聚合物浓度在y轴方向上达到一定峰值是存在一个过度过程的，这是由于在界面处部分聚合物链段延伸到凝固浴中导致的，该部分在除去NMP和水后不能形成具有显著分离效果的固体膜结构，因此在聚合物浓度峰值处设置了一个截止值［图12（A）］，仅计算截止值右侧区域的孔径.由图12（B）可以看出，简谐力场和弹簧力场在对二维孔径分布的影响上具有相似性，膜表面结构相对于内部更加致密.与弹簧力场相比，简谐力场作用下膜表层孔径略小，这是由于聚合物刚性增强，导致水难以穿透膜表层与NMP进行质量交换所致，二维孔径分布表明聚合物链段刚性增强有助于形成更加致密的膜表层.图12（C）为不同力场下的膜的三维孔径分布图.与弹簧力场相比，简谐力场下的膜的孔径分布略宽，但两者的最大孔径是相近的，这表明力场主要影响的是膜表面孔径分布，对内部疏松层的影响并不明显.

Fig.12 Effects of harmonic force field and spring force field on the 2D and 3D pore size distributions

2.2 聚醚砜浓度对NIPS法成膜过程的影响

目前，人们普遍认为NIPS法成膜过程中溶剂和非溶剂的质量交换作用对最终膜结构和性能有着决定性的作用［2］，其中溶剂和非溶剂间的传质与溶剂/非溶剂相互作用、聚合物浓度、聚合物链长以及非溶剂温度等有重要联系.本课题组前期的模拟研究发现［10，11］，在聚合物溶液发生NIPS过程中，聚合物浓度对膜结构的影响更大.因此，本文在简谐力场的条件下探究聚醚砜浓度对相分离过程的影响，并结合前期的工作［11］，对比在简谐力场和弹簧力场条件下聚醚砜浓度对相分离过程的影响.

由图13可以看出，同一浓度下，随着时间的推移膜形貌的变化与图8～图12结果相似.当聚合物浓度较低（8%，体积分数）时，初始时聚合物的高浓度区域较少，且表层更加多孔；当聚合物浓度较高（16%，体积分数）时，由于聚合物链更容易发生聚集，会增加聚合物的局部浓度，从而可以观察到更多的高浓度聚合物区域，且其表层的孔也会更少.这些观察结果与实验结果是一致的［32～34］，即膜表层为致密层，内部为多孔亚层结构.

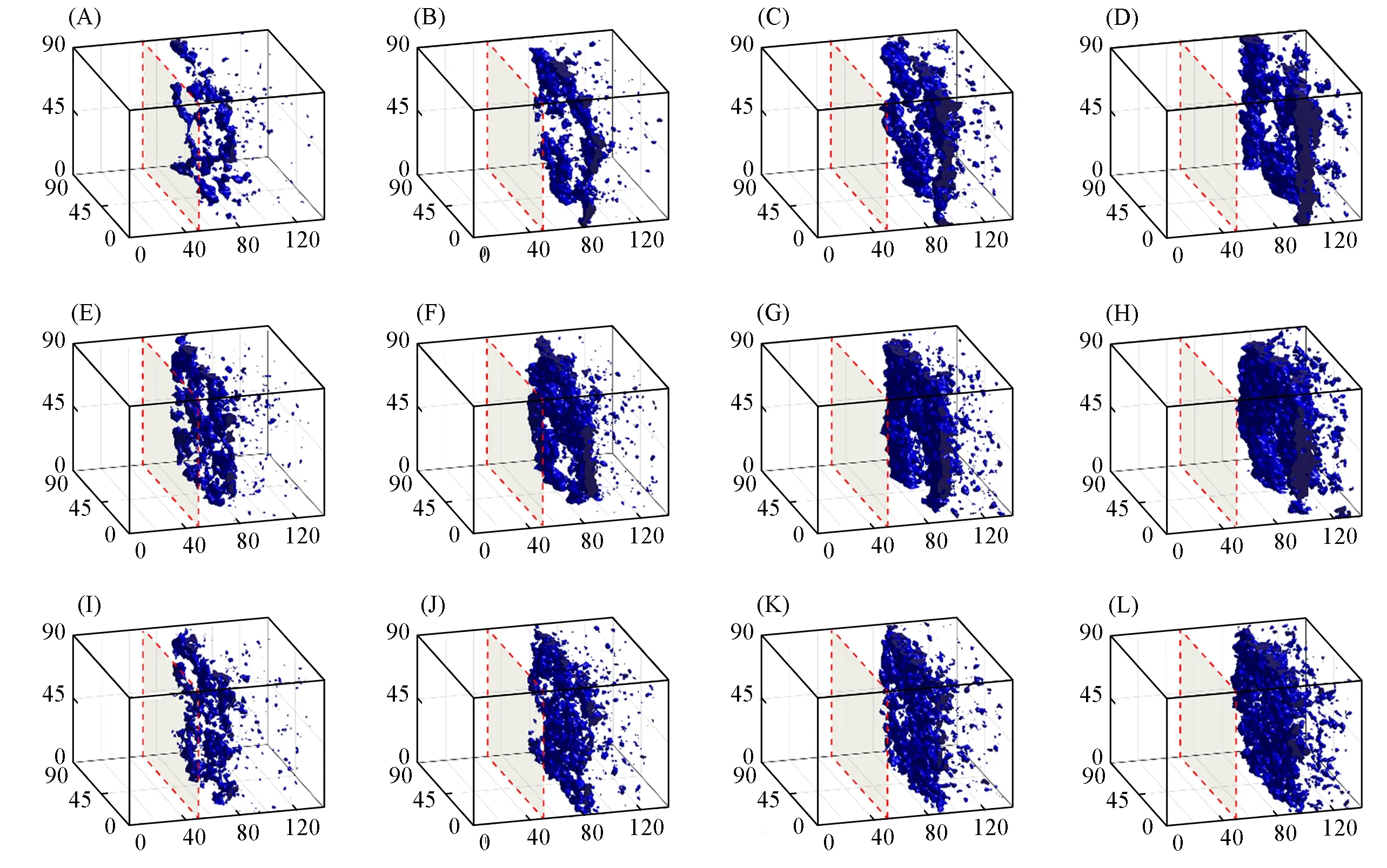
Fig.13 Morphology evolution of the systems with chain length n=90 and initial polymer volume fractions of 8%(A—D),12%(E—H),and 16%(I—L)at 2500τ(A,E,I),5000τ(B,F,J),7500τ(C,G,K)and 10000τ(D,H,L)during the DPD simulations

图14表明，随着时间的推移，峰的高度逐渐增加并向右移动，随着聚合物初始浓度的增加，峰的宽度也缓慢增长，这说明PES浓度的增加会导致在界面附近形成了厚且致密的聚合物层，这与实验观察结果一致［33，35］.此外，随着聚合物浓度的升高，聚合物溶液黏度变得更大，并且所形成的膜表层也会更加致密，进而会导致溶剂与非溶剂的传质减慢，从而延迟相分离，这一现象在图13（D），（H）和（L）的相分离形貌中得以体现.浓度为16%的膜表层明显更加致密，但其厚度却低于浓度为12%的膜表层厚度；这一现象同样可以在图14中观察到，浓度为16%的PES分布密度峰高明显高于12%的，但其峰宽却明显小于12%浓度下的.

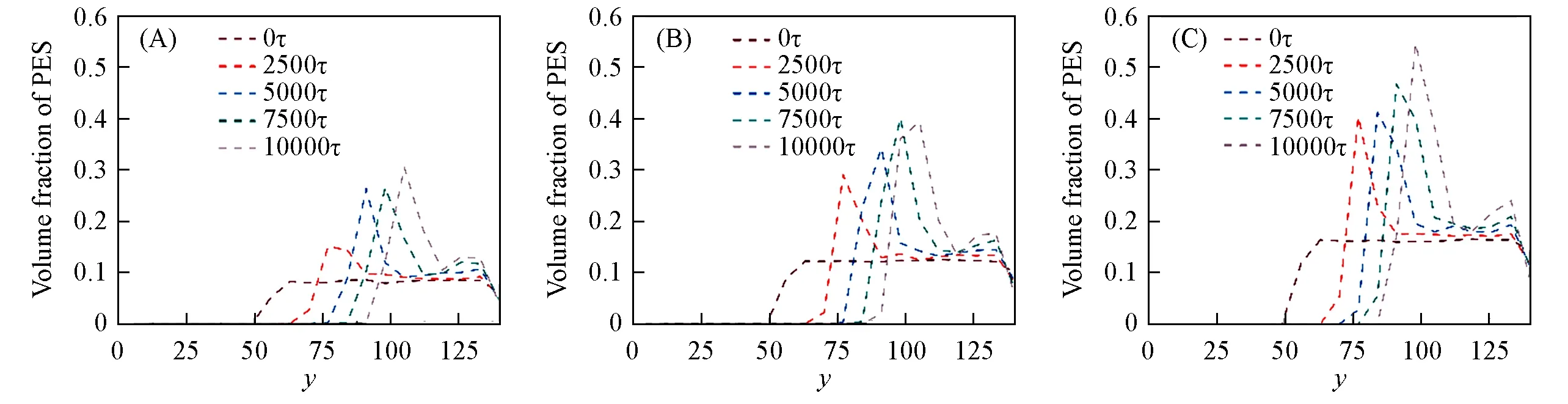
Fig.14 Profiles of volume fractions of PES along y axis at 0,2500τ,5000τ,7500τ and 10000τ

图15（A）给出3种不同的PES浓度条件下，PES的Rg随时间的变化.在初始阶段，Rg下降得很快，而后又缓慢地减小.这可能是因为初始时聚合物链段较为舒展，导致Rg的初始值较大；而随着非溶剂的接触，导致了聚合物链快速聚集，因而Rg快速降低最后趋于稳定.但不同浓度PES溶液的初始Rg也是不同的，浓度为8%，12%和16%时的初始Rg值分别为5.97rc，5.84rc和5.82rc，即当聚合物浓度增加时，初始Rg值会略有降低，这与聚合物溶液理论是一致的［36，37］.但是当体系逐渐稳定后，Rg值却随浓度的增大而减小了.这可能是由于低浓度时，聚合物被溶剂和非溶剂压缩导致其所占空间相对较小，因而分子链更加团聚，所以稳定后浓度低时Rg反而较小.

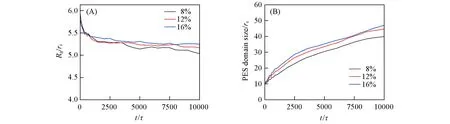
Fig.15 Radius of gyration Rg(A)and domain size(B)as functions of time for the systems with polymer volume fractions of 8%,12%and 16%

图15（B）给出不同浓度下聚合物相区尺寸随时间的变化.由图15（B）可见，随着时间的推移，相区尺寸首先是快速增加，而后增长速度逐渐减缓.初始时相区尺寸快速增加可能是由界面处聚合物层的形成导致的，而后由于膜表层形成导致了物质交换阻力变大，因而相区尺寸增长幅度减小.此外，PES浓度越高，相区尺寸越大，这是因为聚合物浓度越大越容易在NMP与水物质交换的时候析出成膜.

图16（A）给出不同浓度PES的二维分布孔径.可见，不同浓度的孔径分布总体趋势是相同的，膜表层的二维孔径均明显小于内部孔径，这与实验结论一致［34，38］.随着聚合物浓度从8%增加到16%，膜表层孔径明显减小，由7.1rc减小至0.4rc，这与文献中的实验结果符合得很好［33，34］.与前期弹簧力场的模拟结果相比［11］，简谐力场条件下模拟得到的表面孔径更加接近于实验所得到的纳米级孔径［34］，并且在低浓度时（8%）表现尤为明显，表明聚醚砜链段刚性的增强使得模拟体系更加接近实际；但内部疏松层的二维孔径却随着浓度的升高而减小，这是因为聚合物浓度升高在一定程度上阻碍了溶剂与非溶剂的传质作用，导致了内部存在部分溶剂保留的现象，这一现象可以从实验中观察到［34］.图16（B）为不同浓度下膜的三维孔径分布图.随着PES浓度从8%增加到16%，孔径分布会明显变窄，且随着浓度的增加，三维孔径分布峰由7.1rc降至3.9rc，与文献［34］中实验数据的吻合性更好.

Fig.16 Effects of initial polymer volume fraction(8%,12%,16%)on the 2D(x-z plane)pore size profile(A)and 3D pore size distributions(B)

3 结 论

通过从MD模拟映射的方法构建了符合PES刚性结构的DPD简谐力场，证明了不同力场施加下的PES链段刚性对PES/NMP/水体系NIPS过程存在影响.首先，施加不同力场时，在整体上均可得到明显的非对称结构；其次，PES链段刚性的提升能够明显提升体系的相分离速度，同时会导致相界面处的PES薄层形成得更加快速而致密，孔径更小，而对内部的疏松结构影响较小；此外，结合不同力场下聚合物浓度对相分离过程的影响发现，不同PES浓度下，链段刚性的提升对相分离过程的特征和演变趋势没有造成根本性的变化，与经典的弹簧力场的模拟结果在整体趋势上有相似性，这一点也说明了弹簧力场的模拟结果也有相当的参考价值.本文中简谐力场的构建从原理而言并不复杂，但实际操作上较为繁琐且耗时，因此对于一些精确度要求不高的体系而言，经典的弹簧力场依然是简便且有效的方法.