订购和运输原材料的最优方案的研究

向 阳，任 红，耿亚东，詹明强

（西藏民族大学，陕西 咸阳 712082）

1 问题的研究背景

随着经济的发展，物流运输和材料运输也越来越重要。各个企业相互合作，形成一条供应链，体现着各个企业之间的相互利益。从材料运输到成产成品的过程中会有各种问题，如供应商每周的供货量、客户每周的需求量以及物流公司每周的运货量，同时在运输过程中也会有一些损耗。在考虑以上各种因素的基础上寻求最优方案是一件比较复杂是事情，同时各个供应商以往的行为也会影响着人们的抉择。

2 订购和运输原材料最优方案问题及其分析

针对订购和运输原材料最优方案问题，首先以订货量、供货量、稳定性（即供货量和订货量的差值的标准差）和供货效率（供货大于订货的周数），运用专家评价法，得出这4 项指标的权重向量ω1；其次运用熵值法[1]算出4 项指标的权重向量ω2；然后以0.8∶0.2 进行权重修正，算出最终的权重向量ω；最后根据求得的权重向量ω，对这4 项指标进行加权分析，并根据权重向量ω 对每个指标加权求和，得出最终的量化分数，并根据分数排名。

2.1 决策影响因素及其影响机理的分析

为分析决策影响因素及其影响机理，根据分析得出保障企业生产重要性的4 项指标，见图1。

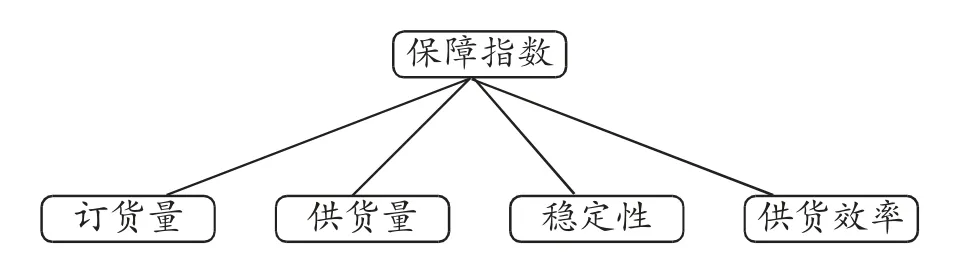
图1 保障企业生产重要性指标示意图

由此得出保障企业生产重要性指标（即保障指数）的4 个主要决策指标，分别为订货量、供货量、稳定性、供货效率。对此4 项指标进行分析，可建立以下模型。

2.2 模型建立与求解

根据以上分析，运用改进的层次分析法，通过考察过去企业的生产影响，结合专家估计，得出最终的权重。

由于专家赋值权重存在一定的主观因素，因此结合运用熵值取权法[1-2]。熵值取权法的优点是可以通过判断各因素的变化剧烈程度来决定此因素在最终目标上所占的权重，具有一定的客观性。因此，可根据专家估计，构造出4 项指标之间的关系矩阵[3-4]为m0=权重向量ω1=[0.055 3 0.565 0 0.262 2 0.117 5]。一致性检验参数为

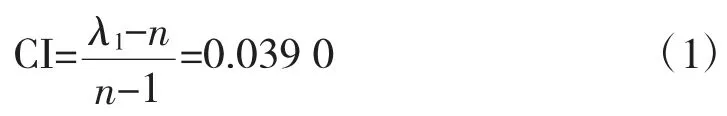
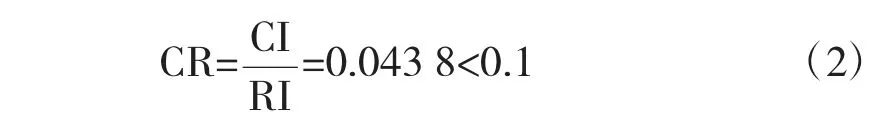
因此，满足一致性检验要求。

同时，又可根据熵值取权法，客观地得出另一个1×4 的权重向量ω2。接着以0.8∶0.2 的比例，修正两种不同方法得出的权重向量，使得到的权重向量更加可信，最终得到总的权重向量ω=[0.170 0 0.457 7 0.216 3 0.156 0]。综上所述，可以建立模型为

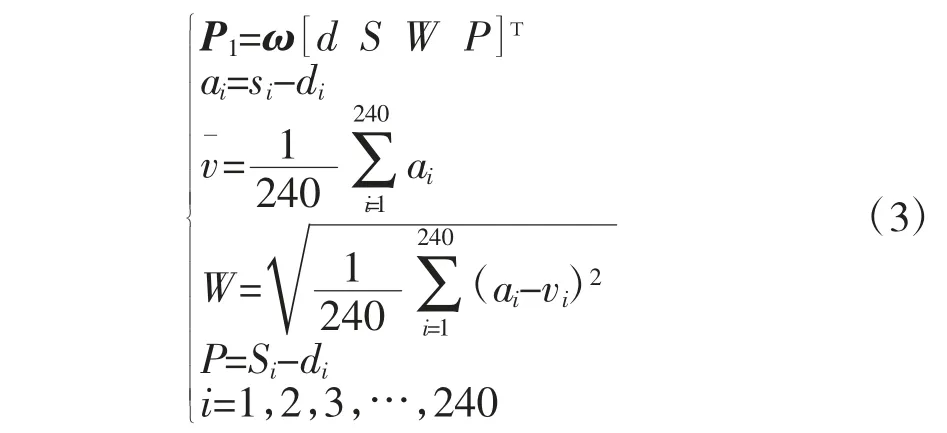
式中：d、S、W、P 分别为订货量、供货量、稳定性、供货效率。

2.3 结果分析

仅运用改进的层次分析法有一定的主观性，结合熵值取权法对得到的权重进行修正，可以得到相对真实可信的结果。由于可以运用此方法对任意数量的供应商进行分析，得出权重排名，因此此方法具有一定的普适性。

3 订购和运输原材料最优方案问题的延伸

虽然在对各个供应商进行量化分析之后已可以得出排名，但是在现实生活中还需要考虑保证生产需求的情况、要求供应商数量最少的情况以及考虑损耗率、经济性等问题的情况，从而考虑原材料的订购方案和运输方案。

3.1 问题分析

本文对企业生产条件作一定的假设：一家企业每周的产能为2.28 万m3，每1 m3需要消耗A 类原材料0.60 m3，或B 类原材料0.66 m3，或C 类原材料0.72 m3，损耗率分别为a1、b1、c1。根据上文对供应商的综合评价与分析，先考虑供应商数量最少但满足生产需求的情况条件，再考虑运输损耗率、每周产量、经济性等问题来建立最优方案，由于延伸问题存在各种约束条件，因此在原问题的基础上建立优先权的动态规划模型。以3 类原材料供应商数量最少值为目标函数，以每种产品生产数量和每周产量为约束条件，μ 为所有供应商损耗率的平均值，xA为A 材料选择供应商数量，同理xB、xC分别为B 原材料、C 原材料的供应商数量，建立以下基于优先权的动态规划模型[5]。

3.2 模型建立

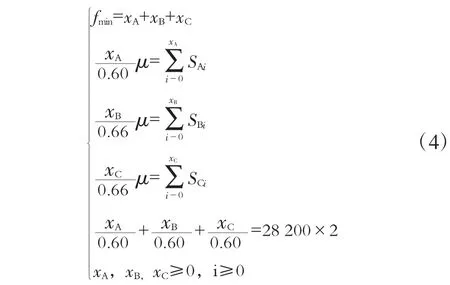
式中：S 为供货量；i 为周数。

3.3 模型求解

根据以上模型，可以通过MATLAB 软件进行科学运算[3-4]。如果确定需要多少周，则可以得出最少需要多少家供应商；同时，如果知道了A、B、C 3 类原材料的单价，便可以求得经济性最高的最优方案。

3.4 模型评价与分析

在原问题的供应商综合评价与量化排名后，再增加新的约束条件，该延伸问题同样可以得以解决，因此可知该模型具有一定的合理性和可行性。

4 结束语

本文主要借助现实生活中的原材料订购与运输问题，结合数学建模思想，首先运用改进的层次分析法进行分析得出各个因素的权重；其次利用熵值取权法对改进的层次分析法得出的权重进行修正，使结果更加可信；最后对各个供应商进行量化分析。进一步地，考虑在保证生产量不变的前提条件下，要求供应商数量最小、最经济的订购和运输原材料的最优方案，先建立基于量化分析排名的优先权的动态规划模型，再求解出最优方案，该模型方法在实际生产和现实生活中有一定的借鉴意义。