一个新的三维混沌系统的特性分析、电路实现

颜闽秀, 谢俊红， 孙靖宇

(1.沈阳化工大学 信息工程学院， 辽宁 沈阳 110142； 2.工业环境-资源协同控制与优化技术辽宁省高校重点实验室， 辽宁 沈阳 110142； 3.北京首钢国际工程技术有限公司， 北京 100041)

混沌[1]作为非线性动力学系统中特有的一种运动形式，由于其具有对初始条件极端敏感性和内在随机性等特征，使其在通信、电子、信息处理等科学领域引起了人们广泛的关注[2].早在1963年，Lorenz意外地发现了第一个混沌吸引子[3].之后，不同类型的新混沌系统随之不断地被发现.1976年，MAY教授提出了Logistic混沌系统模型[4]，新系统比Lorenz系统简单、且拥有不同于Lorenz系统的拓扑结构[5].1999年，CHEN提出了Chen系统[6]，随后LÜ、CHEN接着又提出了LÜ混沌系统[7].此后，不断产生新型的混沌系统，有LIU混沌系统[8]、QI混沌系统[9]、具有切换函数的三维连续混沌系统[10]、含有一个非线性乘积项的四维超混沌系统[11]、拥有恒定Lyapunov指数谱的新混沌系统[12]、产生多翼的四维混沌系统[13].由于混沌信号具有类随机、长期不可预测性等特性，它常被应用于工程领域，如保密通信、信息加密[14]等，并逐渐扩展到天文学、生物学等其他领域[15].为了将更多的混沌系统应用在工程中，必须丰富混沌数目，构造更多的混沌系统.本文在文献[16]的基础上提出一个新型三维自治混沌系统，该系统系数为1，第1个方程和第3个方程各含有一个非线性交叉乘积项为x2x3和x1x2，与一般的Lorenz混沌系统相比系统结构较简单，混沌吸引子较复杂.通过对系统的相轨迹图、功率谱图、分岔图、Lyapunov指数谱等的理论分析和仿真实验，验证了系统的混沌特性.最后，设计合适的电路图，并利用电路软件Multisim模拟仿真，证明了本文提出的新系统电路在物理上是可以实现的.

1 新混沌系统模型及其基本特性分析

1.1 新混沌系统模型

在文献[16]的基础上提出新三维自治混沌系统.与文献[16]相比，最主要差别在于系数和非线性项的不同，文献[16]的系统系数为2，第2个方程的非线性项是交叉乘积项x1x2，第3个方程的非线性项为x2，而该系统系数为1，第1个方程和第3个方程各含有一个非线性交叉乘积项,为x2x3和x1x2，且结构较简单[以下简称为系统(1)]，其动力学方程如下：

(1)

式中a、b是实常数.当a=1、b=1,选取初始值(0.1，0.1，0.1)时，新系统存在的吸引子如图1至图4所示.

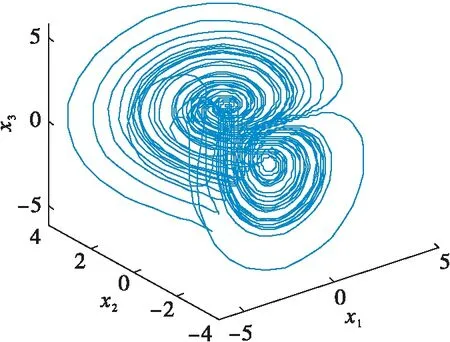
图1 混沌吸引子Fig.1 Chaos attractor

图2 x1-x2相图Fig.2 x1-x2 phase diagram

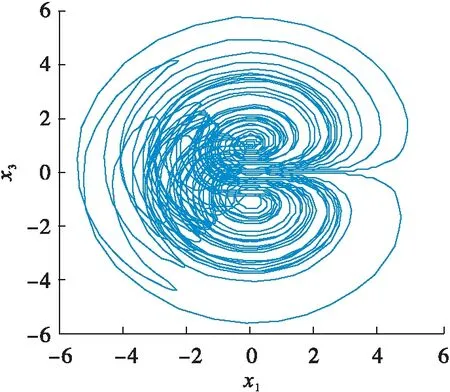
图3 x1-x3相图Fig.3 x1-x3 phase diagram

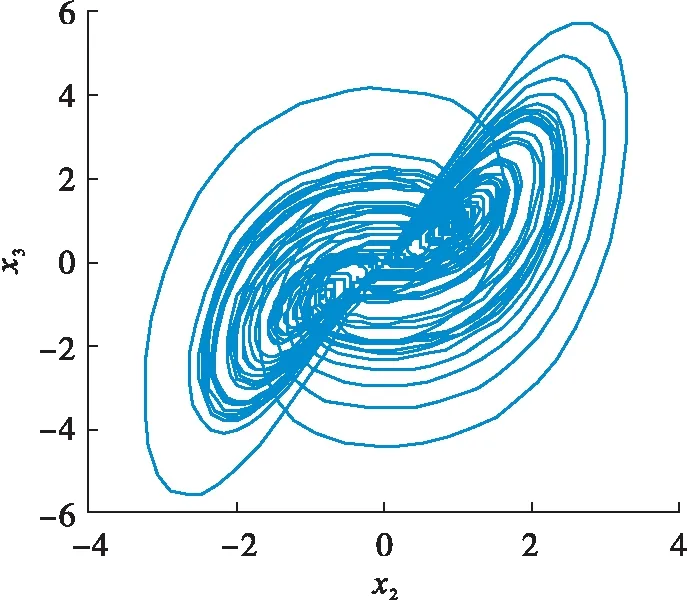
图4 x2-x3相图Fig.4 x2-x3 phase diagram

1.2 李雅普诺夫指数和维数

利用MATLAB，通过正交法求得李雅普诺夫指数为:λL1=0.211,λL2=0,λL2=-1.21,如图5所示.

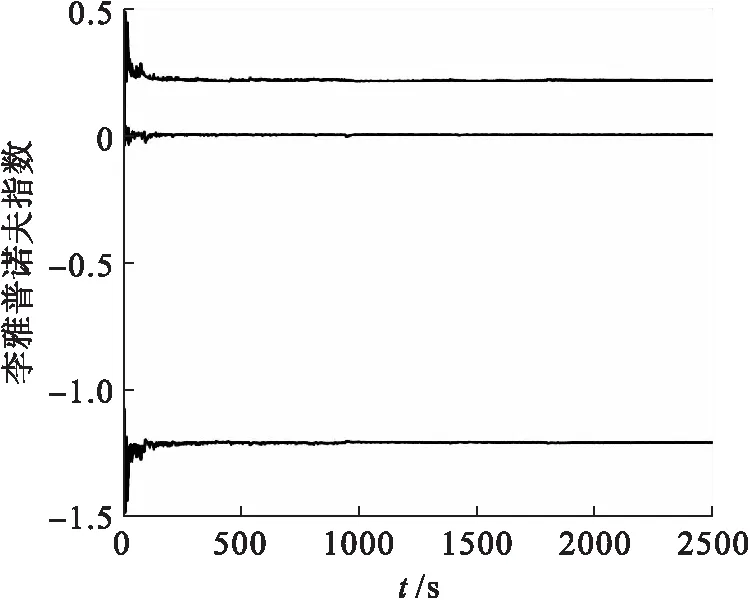
图5 李雅普诺夫指数Fig.5 Lyapunov exponents

计算李雅普诺夫维数得到

(2)

由于系统(1)的Lyapunov指数分别为正值、零值和负值，Lyapunov维数为分数维数，则这个三维非线性动力学系统的混沌解在相空间的表现是在一个一定的区域内无限填充或具有分数维结构的不变集合，所以，可以解释系统(1)是混沌的.

1.3 系统的耗散性和吸引子的存在性

计算系统的耗散度∇V：

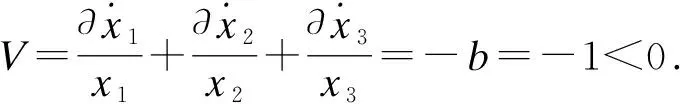
(3)

∇V<0，说明这个三维非线性动力学系统是一个耗散的非线性动力学系统，其指数形式收敛为

(4)

因此，系统的所有轨迹运动被限制在零体积的集合上，其轨道最终将安居在一个不变的吸引子的集合中，这表明了吸引子的存在性.

1.4 平衡点及其稳定性

令系统(1)等式右边等于0，即：

(5)

得到两个平衡点的解，分别为:A(0,-1,-1),B(0,1,1).

在平衡点A(0,-1,-1)，获得雅可比矩阵

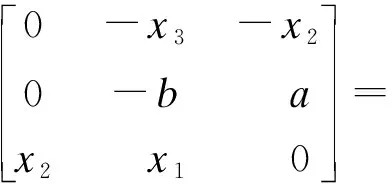
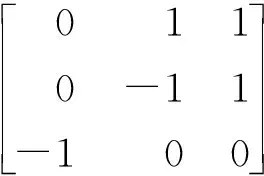
(6)

令det(J1-λE)=0,从而其相应的特征根为：0.176 6-1.203i,0.176 6+1.203i,-1.353.可看出特征根有一个负实根和两个正实部的共轭复数，由Routh-Hurwitz判据可知该平衡点是不稳定的鞍焦点.

在平衡点B=(0，1，1)，获得雅可比矩阵

(7)

同理特征根为：0.176 6-1.203i,0.176 6+1.203i,-1.353.根据特征根情况可确定，特征根有一个负实数和两个正实部的共轭复数，从而可知该平衡点同样也是不稳定的鞍焦点.

1.5 参数变化时系统的分岔图和李雅普诺夫指数谱

当固定参数为b时，令a∈(0.1,8)，给出状态变量x1随参数a逐渐变化时的分岔图和李雅普诺夫指数谱,如图6、图7所示.

图6 系统的a-x1分岔图Fig.6 a-x1 bifurcation diagrams of the system

图7 参数a变化时系统的李雅普诺夫指数Fig.7 Lyapunov exponent of the system when parameter a changes

由图7可看出:当a在区间[0.1,2.4)∪(2.55,5.5]时，系统的最大Lyapunov指数大于0，由混乱密集相点组成的混沌区域出现在分岔图中，这阐明系统处于混沌状态；当a在区间[2.4,2.55)∪(5.5,8]时,系统的最大Lyapunov指数小于0，由混乱密集相点组成的混沌区域没有出现在分岔图中，所以，系统由混沌进入周期状态.

当固定参数a时，令b∈(0.5,2)，状态变量x随参数b逐渐变化时的分岔图和Lyapunov指数谱由MATLAB进行绘制，如图8、图9所示.

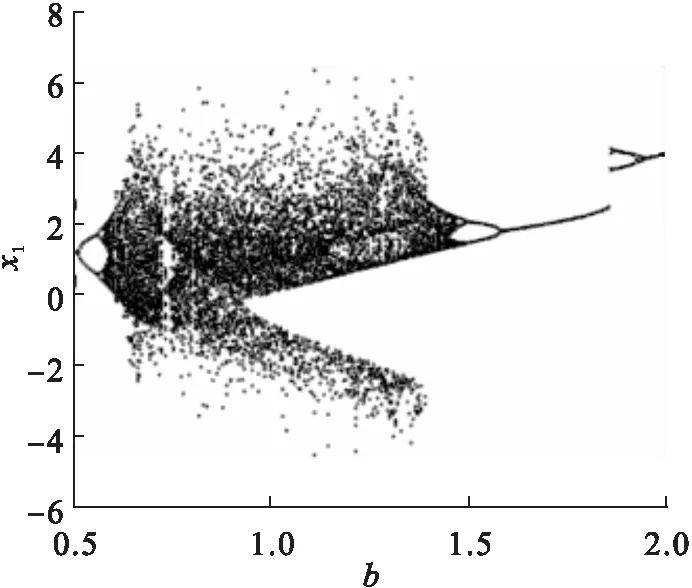
图8 系统的b-x1分岔图Fig.8 b-x1 bifurcation diagrams of the system

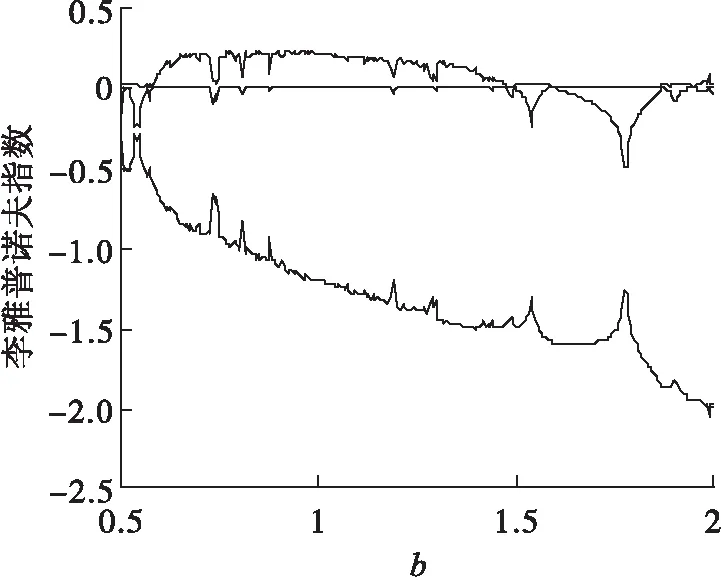
图9 参数b变化时系统的李雅普诺夫指数Fig.9 Lyapunov exponent of the system when parameter b changes

从图9可看出:当b在区间[0.5,0.57)∪[0.735,0.75)∪(1.48,2]时,系统的最大Lyapunov 指数小于0，这意味着系统处于周期状态；当b在区间 [0.57,0.735)∪[0.75,1.48]时,系统的最大Lyapunov大于0，系统从周期开始进入混沌状态，在分岔图中出现的混沌区域是由成片混乱密集相点组成的.

从上述的分岔图和李雅普诺夫指数谱的分析可见，系统的整个状态是由参数a、b的变化决定的，并且系统变量呈现出极其丰富和复杂的混沌动力学行为.因此，验证了该系统的混沌特性.

1.6 系统的频谱图以及庞加莱截面图

观察系统的功率谱图和庞加莱截面的截止点是为了观察这个新的三维非线性混沌系统的动力学特性.绘制系统关于x1的功率谱图和截面x3=1时的庞加莱截面图，分别如图10、图11所示.

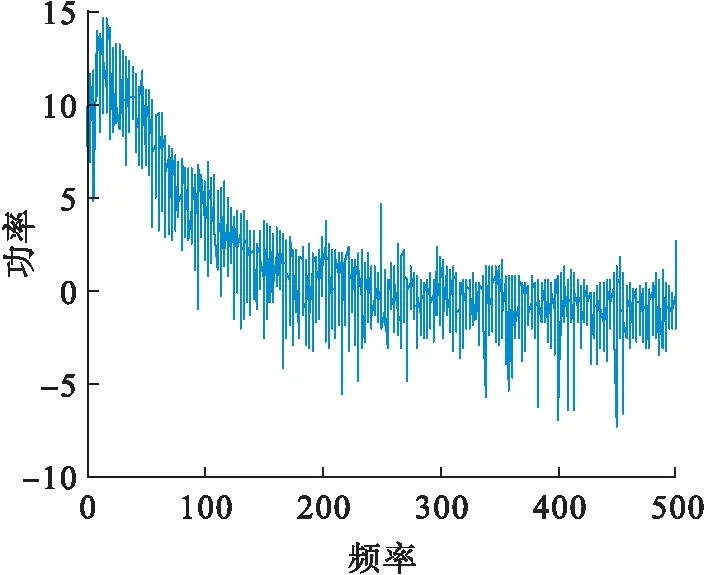
图10 系统的功率谱图Fig.10 Power spectrum of the system

图11 系统的庞加莱截面图Fig.11 Poincare section of the system

通过计算机数值仿真得到这个新的三维非线性自治混沌动力学系统的功率谱图，其频谱是连续谱，没有明显的波峰.而这个新的三维非线性自治混沌动力学系统的庞加莱截面图是一些杂乱无章的点的集合.因此，这反映了混沌动力学系统的一个基本特征.

2 系统电路设计与仿真实现

下面将判断系统(1)能否实现.通常，任一个整数阶三维非线性自治连续平滑动力学系统都能够物理实现，或能够用电子电路实现.由理论分析和仿真结果得到了验证.用Multisim软件实现的电子电路原理图如图12所示.电路采取线性电阻、电容器、运算放大器、模拟乘法器(增益为1).模拟乘法器可应用在实现系统中的非线性乘积项，电容器可应用在实现积分运算中，可借用运算放大器及其相关电阻构成实现加、减以及积分运算模块.

图12 系统的混沌系统电路原理图Fig.12 Circuit diagram of chaotic system

根据基尔霍夫电流定律和基尔霍夫电压定律写方程，则有：

(8)

与系统(1)相比，公式(8)中的线性电容值以及线性电阻值分别取为：

(9)

依据上述数据，对所设计的混沌电子电路进行仿真，结果如图13至图15所示.从图13、图14、图15可以发现，这个新的电路能够产生混沌现象,且能产生复杂而丰富的非线性动力学行为.通过电路仿真、数值计算和理论分析,其结果显然完全一致，这也证实了提出的混沌系统是一种新的混沌系统，而且可以在电路中实现.

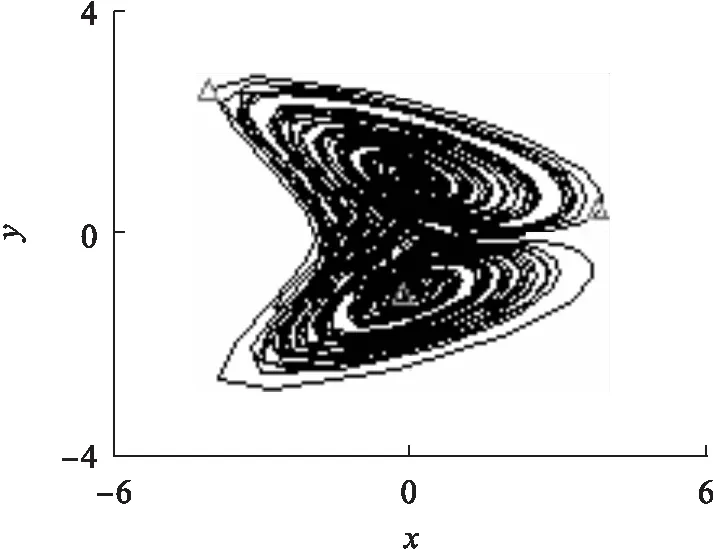
图13 x-y相图Fig.13 x-y phase diagram

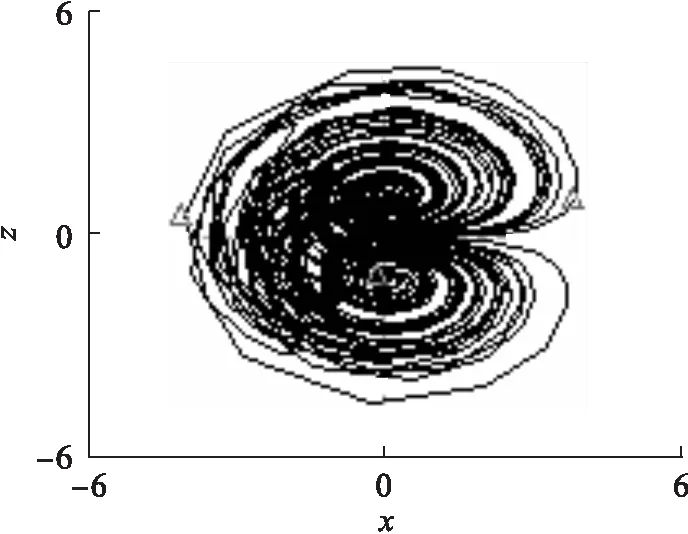
图14 x-z相图Fig.14 x-z phase diagram

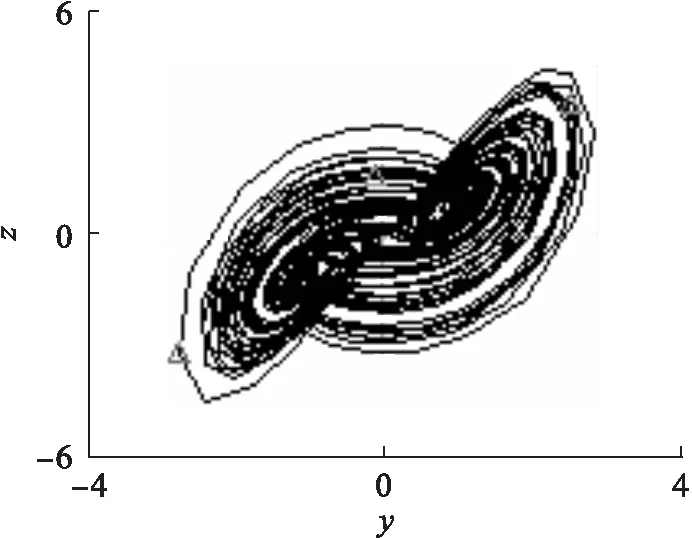
图15 y-z相图Fig.15 y-z phase diagram

3 结 论

提出了一个新的三维混沌系统.新系统具有丰富的动力学行为.通过理论分析、计算机数值仿真、Lyapunov及其维数、平衡点及其稳定性、耗散性及其存在性、分岔图及其Lyapunov指数谱等对新的三维混沌系统的动力学特性进行了检验.由此可见，所提出的混沌系统具有较为复杂的动态行为，应用在工程中有很大潜力.遵循系统方程设计了电路仿真实验，并且由混沌系统模型搭建电路进行进一步验证，由此确认了此新系统的物理可完成性.所设计的混沌电路，可使用在混沌的通信保密以及信息加密之中，同时也可当作系统的有效信号发生器.但是，该系统在同步控制的方法上有待进一步研究.