主成分分析阈值选择差异性分析研究

张 婧，刘 倩

（1.兰州石化职业技术大学，兰州 730070；2.国家电网兰州供电公司，兰州 730050）

引 言

主成分分析（Principal component analysis，PCA）是特征提取和降维的一种方法，其目的是将一系列具有相关关系的多个指标或影响因子转化为一组新的相互独立的综合指标，在转化的同时尽可能多地保留原始变量的信息，以实现对多变量的降维，从而降低问题的复杂度［1］。关于主成分阈值选择的标准，文献［2］明确给出了选择依据，即：“保留特征值大于平均特征值的主成分，对于一个相关矩阵，对应的平均特征值为1”。文献［3］对核心主成分代表的含义进行了解释和分析。具体地，文献［1］选择95%作为主成分阈值；文献［4］选择90%作为阈值；文献［5］以99%作为阈值；文献［6］同样选择99%作为阈值；文献［7］中没有说明具体阈值选择多少，而是将维度从784维降到441维；文献［8］分别选择95%、97%和99%作为阈值，进行了数字图像压缩；而文献［9］选择76%的主成分，将原有11维数据降至4维；文献［10］中对于分布鲁棒的有条件风险值和风险规避的生产-运输问题，提出的PCA仅使用50%的主成分，得到近似解（在1%以内），计算时间减少了1～2个数量级。

综合以上分析，很多应用以平均特征值作为选择主成分的标准，但是阈值选择低于该标准应用结果是否会降低，并没有明确的分析。因此本文提出一种PCA阈值选择差异性的实验分析方法，并选择PCA-BP神经网络对手写体数字进行分类，研究主成分阈值与分类结果之间的变化关系。为了使结果具有可比较性，选择来自美国国家标准与技术研究所的手写体数据集MNIST作为样本进行实验。结果表明本文得出的阈值选择差异性分析结果可以为不同应用中主成分分析阈值的选择提供依据。

1 基本算法

1.1 主成分分析

（1）主成分分析原理

主成分分析就是将原来的p个变量，通过线性组合方式生成p个包含原有变量信息的综合变量，组合方式表示为

将上述线性组合方式用向量方式重写为Fj=αj1x1+αj2x2+…+αjp xp，j=1，2，…，p。同时应该具有以下3个条件：

①两者互不相关，即Cov(Fi，Fj)=0。

②F1的Var(F1)最大，F2的Var(F2)次之，以此类推，Fp的Var(Fp)最小。

因此，本文将Var(F)最大的称为第1主成分，即F1；将Var(F)次之的称为第2主成分，即F2；以此类推，Var(F1)最小的为第p主成分，即Fp。其中aij称为主成分系数。

（2）主成分选择

在主成分分析中可以获得与原变量维度相同的p综合变量，且对应的方差依次递减，相应的所含原变量数据的信息也递减。在实际应用中，如果将这p个主成分全部使用，则达不到降维的效果。而且根据方差，前面几个主要的成分基本上包含了绝大多数原始数据信息，因此p个主成分不用全选。主成分的选择方法是以每个主成分的累计贡献率作为依据，根据其大小选择前k个。其中贡献率指该主成分的方差占所有主成分方差和的比重，用贡献率βi来表示，表达式为

贡献率βi的大小反应了该主成分包含原变量信息的多少，其中选择多少个主成分一般以平均特征值作为依据。

（3）主成分分析

对MNIST数据集进行主成分分析，根据单个主成分贡献率以及累计主成分贡献率，绘制主成分贡献率直方图，如图1所示。

图1 主成分贡献率Fig.1 Contribution rate of principal components

为了直观感受PCA分析降维以后与原图的区别，这里选择将维度下降到86维、96维、99维的数据，进行反向还原处理，然后对图像进行重构，由于样本数量较大，选择训练数据的前100个样本进行还原对比，如图2所示。

图2 降维后数据重构对比Fig.2 Comparison of data reconstruction after dimensionality reduction

1.2 PCA-BP神经网络分类模型

（1）BP神经网络

BP神经网络有输入层、隐含层和输出层3层构成，典型的网络结构如图3所示［11］。网络激活函数选择Sigmoid函数，通过反向传播输出层误差，调整权重值与偏置使得代价函数C=最小。

图3 神经网络结构Fig.3 Neural network structure

在实际使用过程中，将反向传播算法与随机梯度下降等算法进行结合使用，从而能计算许多训练样本所对应的梯度。例如给定一个大小为m的小批量数据，下面对小批量数据应用梯度下降学习算法进行描述：

①输入训练样本的集合。

②对每个训练样本x：设置对应的输入激活ax，1，并执行下面的步骤：

前向传播：对每一层l=2，3，…，L，计算zx，l=wlax，l-1+bl和ax，l=σ(zx，l)。

输出误差δx，L：计算误差向量δx，L=∇aCx⊙σ′(zx，L)。

反向传播误差：对每一层l=L-1，L-2，…，2（除了输出层和输入层），计算δx，l=((wl+1)T·

③梯度下降：对每一个l=L-1，L-2，…，2根据更新权重和偏置。

（2）分类模型

PCA-BP神经网络分类模型如图4所示。基于PCA神经网络的分类识别步骤为：

图4 PCA-BP神经网络分类模型Fig.4 PCA-BP neural network classification model

①获取数据且进行预处理并归一化。

②进行样本的主成分分析，对预处理后的样本集进行主成分分析，选择特征值大于平均特征值的m个主成分作为新的训练和测试样本。

③根据不同主成分，创建不同结构的神经网络，进行训练，最后进行测试。

④将第3步的测试结果与没有主成分分析的测试结果进行比较，观测效果是否降低，训练效率是否提升。

2 仿真结果与分析

应用PCA分析，将MNIST数据的784维降至10、20、30、40、41、42、43、44、45、46、47、48、49、50、58、86、153和330维，然后分别选择隐含层神经元个数为30和100，与原784维分类结果进行比较。由于维数过多，因此选择部分对比结果，结果如图5所示，其中第1行为隐含层神经元个数为30的对比结果，第2行为隐含层神经元个数为100的对比结果。

图5 降维后分类结果对比Fig.5 Comparison of classification results after dimensionality reduction

通过图5的分析可知，增加隐含层神经元个数，对于分类结果有明显的提升。而维度从10～330分类结果明显是从低到高再到低的一种变化规律。主成分分析在降维的同时，提高了网络学习的效率，不同维度学习时间对比如图6所示。从图6分析可知，降维大大提高了网络的学习效率，所用时间与维度的关系近似为线性。

图6 不同维度学习时间Fig.6 Learning time in different dimensions

为了更好地说明分类准确率、主成分阈值（累计方差贡献率）和维度之间的关系，分别对隐含层神经元个数为30和100时，每个维度的最高分类准确率和主成分阈值进行仿真，结果如图7所示。

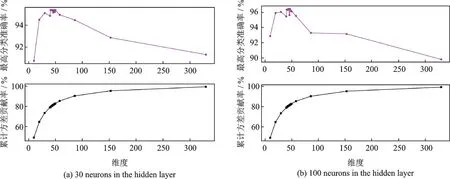
图7 不同维度分类准确率与主成分阈值对比Fig.7 Comparison of classification accuracy and principal component thresholds in different dimensions

通过仿真结果可以看出方差累计贡献率与维度之间是正相关的。随着维度的增加，分类准确率也随之增加，当维度到50维以后，分类准确率明显减小。维度最密集区也是分类准确率最高区域，对应维度是41～50维之间，对应方差累计贡献率在79%～81%之间。58、153和330维对应方差累计贡献率分别为85%、90%、99%。因此，依据平均特征值作为阈值，保证了原有数据信息最大程度不丢失，但不能作为应用的硬性标准。

3 结束语

本文提出一种主成分阈值选择差异性的实验分析方法，通过研究得出降维大大提高了网络的学习效率，所用时间与维度的关系近似为线性。维度与累计方差贡献率正相关。随着维度的增加，分类准确率也随之增加，当但维度增加到50维以后，分类准确率明显减小。维度最密集区也是分类准确率最高区域，对应维度在41～50维之间，对应方差累计贡献率为79%～81%。因此，平均特征值作为阈值并不能作为其他应用的一个阈值，且主成分的提高并不会使分类准确率提高。但是根据降维后数据重构对比图（图2）发现，维度在小于86的范围内，信息识别难度加大，分析其原因是由于其数据主要结构特征在79%～81%范围形成，随着结构特征增加反而影响应用结果。