一种基于邻域近似精度的离群点检测方法

张玉婷，冯 山

（1.四川师范大学计算机科学学院，成都 610068；2.四川师范大学数学科学学院，成都 610068）

引 言

离群点检测多用于入侵检测、信用卡诈骗和医学诊断等领域［1-2］，有分布式［3］、深度［4］、距离［5-6］、密度［7］和聚类［8］等方法。分布式检测要预设数据分布规律，不适合分布未知情形；深度法针对高维数据，效率低；距离和密度法由于利用欧式距离来设计，所以不是检测标称或混合属性离群点的最佳方法；聚类法开销大。

粒计算作为一个重要的研究方向，它主要分为2类：（1）以处理不确定性为主要目标，如以模糊处理和粗糙集为基础的计算模型；（2）以多粒度计算为目标，如商空间理论。其中，经典粗糙集理论模型［9］已经成功应用于标称特征选择和相关性分析等研究。近年来，针对距离和密度法不能有效处理包含标称属性数据的不足，提出了多种基于粗糙集的方法。例如，基于经典粗糙集，文献［10］采用粒计算的思想构建对象离群因子并做离群检测。文献［11］用粗糙边界定义对象异常度以做离群检测。文献［12］用粗糙集隶属度扩展了一种新方法。文献［13］提出了基于粗糙边界和距离的离群检测。文献［14］提出了基于经典近似精度的离群检测。但它们采用等价关系的方式建立数学模型，其检测模型均只适于处理标称属性数据集。

基于邻域粗糙集的特征选择［15-16］能有效处理混合属性数据集。例如，文献［17］提出了基于邻域模型的邻域离群检测。然而，其对参数选择非常敏感。文献［18-21］提出了面向混合属性数据的离群检测。但这些方法均未考虑邻域粗糙度量的离群点检测模型。邻域粗糙度量主要包括邻域近似精度和邻域粗糙度量等［16］，它是度量混合属性数据不确定性的有效方法，可以用于混合属性数据集的离群点检测建模。

针对混合属性离群点检测问题，本文构造了一种基于邻域近似精度的离群点检测方法（Neighborhood approximation accuracy-based outlier detection，NAAOD）。该方法以优选异构邻域关系度量和统计邻域半径构建邻域信息系统（Neighborhood information system，NIS），以邻域近似精度离群因子表征对象离群度。对比实验表明，NAAOD算法能同时适于各种属性组合的离群检测。

1 预备知识

假设信息系统IS=(U，A，V，f)，其中U={x1，x2，…，xn}，属性集A非空为属性a的值域；f：U×A→V，∀a∈A和∀x∈U，f(x，a)∈Va。当A=C∪D时，信息系统变为决策系统，简记为DS=(U，C∪D，V，f)，其 中C={c1，c2，…，cm}且D={d}。为 讨 论方 便，设B⊆C且|·|为集 合的势。

定义1［15］论域对象xi的B邻域∀xi∈U和∀B⊆C，δB(xi)={xj|xj∈U，ΔB(xi，xj)≤ε}是xi的B邻域，ε是邻域半径，ΔB(xi，xj)是距离函数。对∀xi，xj，xk∈U，有：

（1）ΔB(xi，xj)≥0⇔xi=xj，ΔB(xi，xj)=0；

（2）ΔB(xi，xj)=ΔB(xj，xi)；

（3）ΔB(xi，xk)≤ΔB(xi，xj)+ΔB(xj，xk)。

例如，关于条件属性子集C的混合欧式重叠度量（Heterogeneous euclidean overlap metric，HEOM）［22］为其中

式中ω{cj}为cj的权重。显然，式（1）可同时处理数值、标称属性及属性值未知情形。δB(xi)为关于属性子集B的以xi为中心的邻域粒，ε=0时退化为等价类。

∀xi∈U，δ(xi)∉∅且称{δB(xi)|xi∈U}覆盖论域U。U上邻域关系N B可写成关系矩阵易知N B是相似关系，邻域内样本彼此相似，δB(xi)是0-1向量，即

2 基于邻域近似精度的混合离群点检测

2.1 检测方法

可用最小-最大归一化［18］对数据集属性和维数差异作量纲统一。同HEOM，异构邻域关系度量（Heterogeneous neighborhood relation metric，HNRM）可定义如下：

定义4对给定，∀xi，xj∈U，B={cj1，cj2，…，cjl}(1≤l≤m)⊆C，xi与xj的混合或HNRM值，其中

易知，式（2）可同时度量不同属性组合的对象差异度，但ε一般由专家确定［17，19，21］，其主观随意性会导致算法对参数敏感。为此，文献［18］提出了具有自适应特性的ε取值法，即

式中：std(cj)为属性标准差；λ为调整参数。显然，式（3）的邻域半径ε取值方式更为合理，它用于调整邻域半径。

性质1条件属性子集并的邻域关系等价于其邻域关系的交，即对

假设C1，C2⊆C分别为数值型和标称型条件属性子集。由性质1易知，对象x的邻域有如下等式成立：

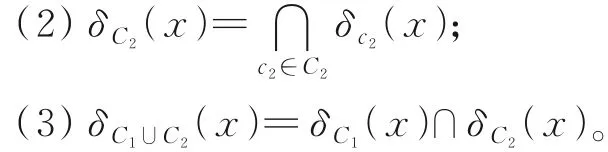
对x∈U和U上邻域关系，可得x的一组邻域粒。利用x的邻域粒差异或距离等信息可以进行离群检测。一般而言，为计算x的离群度，可先算邻域粒离群度，再确定离群因子。邻域粒离群度可用邻域粒的邻域近似精度度量。

定义5特定邻域近似精度关于NE的邻域近似精度可定义为

邻域近似精度常用来度量决策类的论域近似度。一般来说，δB(xi)对一组邻域关系近似精度很低时表明δB(xi)行为异常或离群程度高。而经典近似精度离群因子［14］仅适于度量标称属性。对混合属性，可用邻域粒离群度（Neighborhood granule outlier degree，NGOD）和邻域近似精度离群因子（Neighborhood approximation accuracy-based outlier factor，NAAOF）有效度量。前者度量给定邻域粒的离群程度，后者度量给定对象的离群程度。

式中δB(xi)对一组邻域关系的近似精度很低时δB(xi)对邻域关系影响小，可认为δB(xi)行为异常且离群度高。此时，NGOD(δB(xi))大，可以度量δB(xi)的异常性，进而度量xi的离群性。基于NGOD的邻域近似精度离群因子，即论域对象xi的NAAOF定义如下：

定义7xi∈U的邻域近似精度离群因子可定义为

2.2 检测算法步骤及复杂度

算法步骤如下：

输入：IS=(U，C，V，f)，邻域离群阈值μ，调整参数λ

输出：离群点集OS

算法复杂度：第（2）步的频度为(n×n)，对第（3～12）步的频度为m×(m+1+(m-1)×n)，第（13～18）步的频度为n。故整体的频度为(n2+m2×n+m2+m+n-m×n)。因此，算法的时间复杂度为O(m2n)，空间复杂度为O(mn)。

3 数据实验及结果

实验以文献［14，18］预处理方法为基础，并与适于标称的基于粒计算和粗糙集的离群检测（Outlier detection based on granular computing and rough set theory，ODGrCR）［14］、基于粒计算（Granular computing，GrC）的方法［10］、基于粗糙隶属度函数（Rough membership function，RMF）的方法［12］、适于数值属性的基于距离（Distance，DIS）的方法［5］以及适于混合属性的基于邻域信息熵的离群检测（Neighborhood information entropy-based outlier detection，NIEOD）［19］和基于邻域值差异度量的离群检测（Neighborhood value different metric-based outlier detection，NVDMOD）［20］算法进行对比，以验证NAAOD算法的有效性。最后，从文献［18］中选择了6个离群点检测数据集（含标称、数值和混合属性）。这些数据集分别为Cred、Germ、Heart、Lymp、Wbc和Yeast。进一步，它们被分别导入信息系统ISC、ISG、ISH、ISL、ISW和ISY。为便于比较，同文献［14］的策略，分别从离群点数据集中选取2个子集，最终实验数据子集的基本特征信息描述如表1所示。

表1 实验数据集描述Table 1 Description of experimental data set

以离群点覆盖率（Coverage ratio，CR）［19，23］来评价所提算法。设OStopk(X)是X中离群值排前k的对象，OStrue(X)是真实离群点，则|OStopk(X)∩OStrue(X)|即检测出的真实离群点数。易知，CR(k)=|OStopk(X)∩OStrue(X)|/|OStrue(X)|为离群点覆盖率。显然，TR(k)不变时，CR(k)越大算法性能越好。在实验中，取k=|OStrue(X)|时的离群点覆盖率作为最终对比结果。

对于NAAOD、NIEOD和NVDMOD算法，其参数调节范围均为［0.1，2］且步长为0.1。最终，最优覆盖率作为实验结果。GrC算法的粒距离采用重叠距离法度量［10］。在粗糙集方法中，Lymphography和Wisconsin Breast Cancer对象的属性值均被当作标称类型［8］。除Yeast数据集，用MDL［24］离散化数值属性外，其他数值属性均使用Weka中等宽的离散化方法，其中离散化区间数为3。DIS算法采用欧氏距离度量和最小-最大归一化预处理。

NAAOD算法与对比算法在代表子集上的实验对比结果如表2所示。从表2中可以看出，NAAOD算法在6个混合属性数据子集上实现了较优的结果。例如，在C1上，NAAOD算法的覆盖率为88.00%，与NIEOD和NVDMOD算法相等。而对于ODGrCR、GrC、RMF和DIS算法，其覆盖率分别为60.00%、28.00%、64.00%、68.00%，均小于NAAOD算法的覆盖率。因此，本文所提方法适用于混合属性数据的离群点检测。

此外，NAAOD算法在两个标称属性数据上均取得了最高的覆盖率。表2显示，NAAOD算法在两个标称属性数据上的覆盖率为100%，即它能检测出全部离群点。然而，对于其他方法的覆盖率均小于或等于100%。同理，通过表2可以看出NAAOD算法在大部分数值属性数据的覆盖率均大于或等于其他对比算法。通过上述分析表明NAAOD算法也能有效处理标称和数值属性数据集。

表2 对比实验结果Table 2 Results of comparative experiments %

阈值λ在NAAOD算法中起着重要的作用。C1和W2数据集被选取来探索参数对实验结果的敏感性。在C1和W2数据集上，其覆盖率随参数λ的变化曲线如图1所示。从图1可以看出在大部分数据集上随λ增加，其覆盖率先增加，然后呈现出趋于平衡的趋势。同时，也可以看到对于不同的数据集可以在多个参数λ值下取得最优值。

图1 在C1和W2数据集上覆盖率随参数λ的变化曲线Fig.1 Variation curves of coverage rates with parameters λ on C1 and W2 datasets

4 结束语

基于邻域粗糙集框架，围绕混合属性离群检测问题，提出了基于邻域近似精度的具有自适应特性的离群检测方法。其离群因子融入了具有自适应特性的HNRM度量，且数值型属性无需离散化，能处理混合型数据集。数据实验结果表明，NAAOD算法能有效处理数值、标称和混合型属性数据集。接下来将从三支决策角度进一步研究基于粗糙集模型的其他相关离群点检测方法。