品数学文化 探微课教学
——以“赵爽弦图”为例
黄丽娟
(福建省莆田市城厢区霞林学校,福建 莆田 351100)
一、背景介绍
“赵爽弦图”被誉为中国数学界的图腾,2002年在北京召开的国际数学家大会上,就以此为会徽,足以见得它的完美赵爽是三国时期非常有名的数学家,他大约在222年的时候深入研究了《周髀算经》,书中的一段530余字的“勾股圆方图”(后称“赵爽弦图”,其简图如图1)注文是数学史上极有价值的文献,这个注文也让赵爽对勾股定理产生新的证明方法
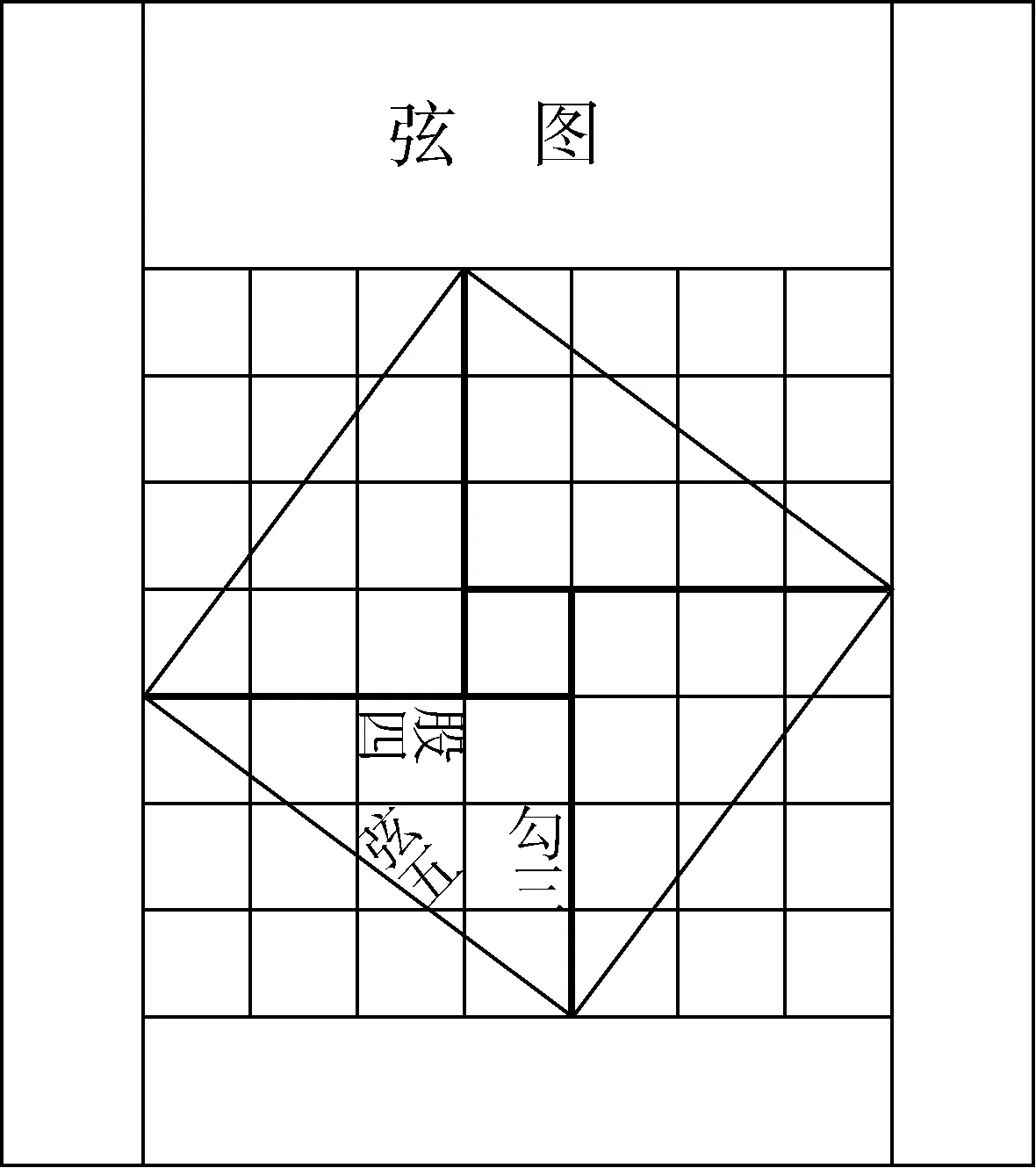
图1
这个新的证明方法是这样表述的:弦图(如图1),又可以勾、股相乘为朱实二,倍之为朱实四;以勾、股之差自相乘为中黄实;加差实,亦成弦实赵爽的这个证明可谓别具匠心,他通过几何的拼、补、割,证明代数之间的恒等关系,既具严密性又具直观性,为中国古代以形证数、形数统一,让代数和几何紧密结合树立了一个典范
二、中考链接
近年来,中考与“赵爽弦图”有着千丝万缕的联系,各地市的考试也都能找到“赵爽弦图”的影子
【典型例题A层】
(2018·莆田)如图2,四个全等的直角三角形围成一个大正方形,中间阴影部分是一个小正方形,这样就组成一个“赵爽弦图”,若=5,=4,则正方形的面积为________
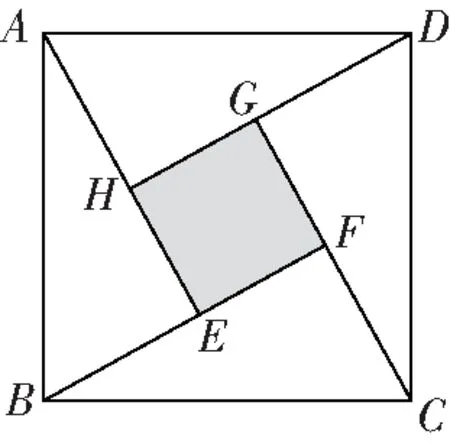
图2
小结:(如图3)
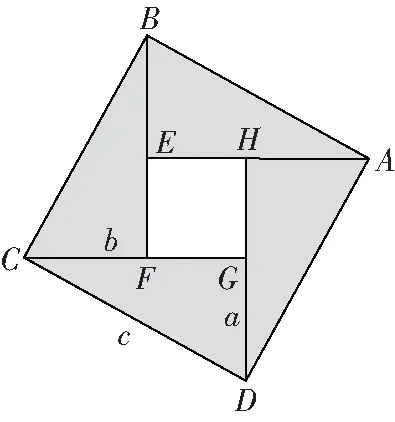
图3
勾股定理:=+,=-,
正方形==+,
正方形=(-),
4△=正方形-正方形=-(-)=+-(-)=2
【A层变式】
1(2020·宁夏)2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》(如图4所示),其中大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边长为,较长直角边长为如果将四个全等的直角三角形按如图5所示的形式摆放,那么图5中最大正方形的面积为________
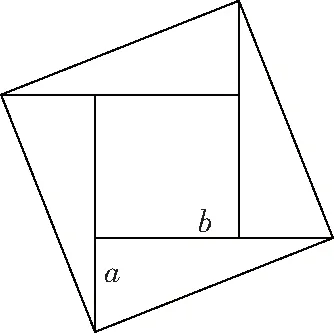
图4
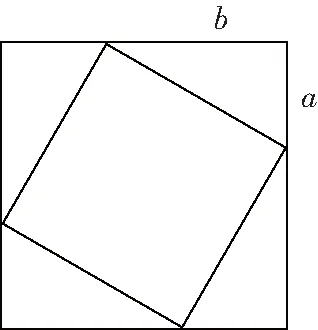
图5
2如图6所示,2002年8月在北京召开的国际数学家大会会标如图所示,它是由4个直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形最小的锐角为,大正方形的面积为25,小正方形的面积为1,则cos=________
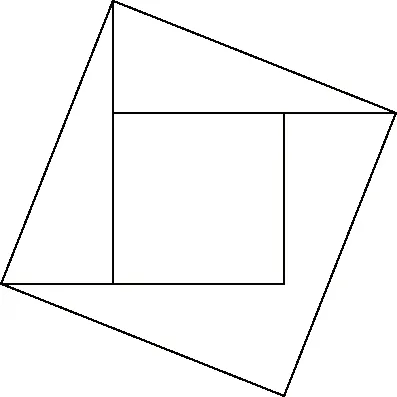
图6
小结:变式的两道题都可以通过前面的小结进行解题,在讲解这两道题时可以从两个不同角度进行引导,其中第1题从已知条件出发,第2题则是从问题出发,让学生体验“逆向思维”的美妙
【典型例题B层】

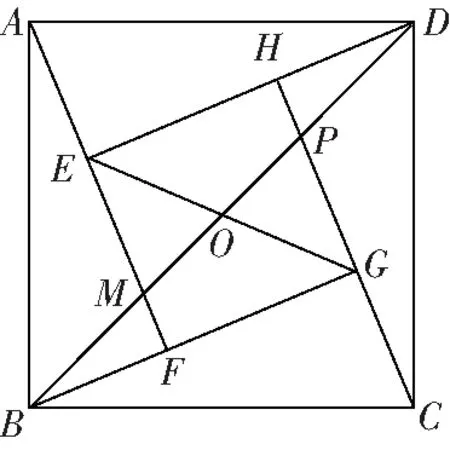
图7

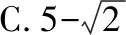
思路分析:
本道例题可以一题多解,结合本题的题型特征,方法一,可以采用选择题中较为常用的赋值法,如设题目中涉及的线段为单位“1”,再结合相似求出它们的面积比;方法二,结合弦图模型面积相等的关系,再结合三角形相似求得面积之比;方法三,可以直接通过正方形的性质,全等三角形等几何图形的相关知识,求出面积比
【典型例题C层】
如图8所示,正方形的边长为10,==8,==6,连接,则线段的长为________
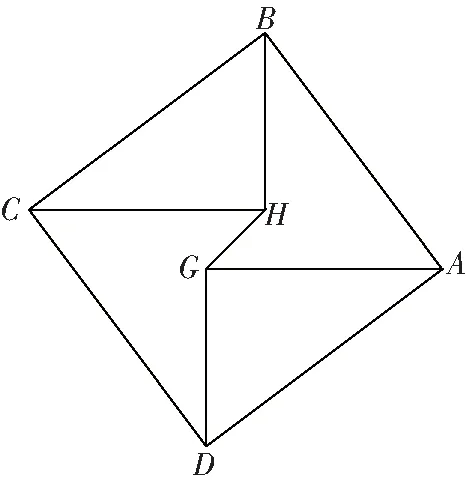
图8
【C层变式】
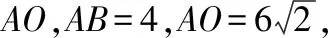
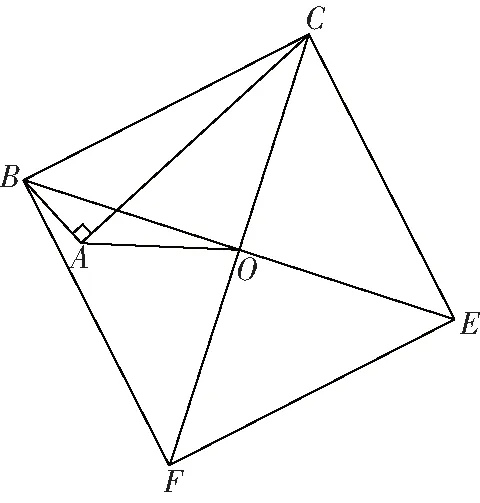
图9
小结:在解决正方形问题时,分析已知条件,再结合“赵爽弦图”的结构特征,通过补全“赵爽弦图”进行解题,能够为我们的解题带来便捷
三、实践思考
(一)尊重学生最近发展区,关注数学问题的变式
数学家哈尔莫斯说过,“问题是数学的心脏”在本微课中,教师结合学生接受问题的难易程度,设置了A,B,C三个层面的问题,这三层的问题由浅入深、层层递进,设置问题时有意识地让问题起点低,入口宽,同时在合适的时候对问题进行相应的变式,以求一题多变,提升学生的思维在设计本微课时,教师考虑到“赵爽弦图”是在勾股定理的证明时引入的,由等积法作为铺垫,学生在此前已有一定的逻辑基础.因此,在尊重学生最近发展区的前提下,A层问题主要考查“赵爽弦图”中的面积问题,在知识生成部分,教师可对例题进行适当的问题变式,帮助学生建立知识间的内在联系,发散学生的思维,培养学生灵活多变的思维品质.最后的C层题目中是在原有例题的基础上进行合理的变式,这样处理的目的是打破学生思维的平衡,引起学生适当的焦虑,刺激学生努力去思考问题,如果学生有障碍,就有了继续观看下去的内驱力.
(二)构建逻辑连贯,走出思维迷宫
著名数学家庞加莱这样说道:“逻辑用于证明,直觉用于发明”赵爽为了证明勾股定理,进行了一系列的变换他的证明之巧,心思之细腻无与伦比本微课在勾股定理的论证方面不予累赘,在微课中通过一系列的习题展示数学严谨的逻辑思维微课中三个层面的习题先由最简单的直接套用公式,再到有弦图的模型,结合相似等知识进行巩固,最后撤掉弦图的模型,需要自己添加辅助线构造模型,以此来达到由浅入深、深入浅出的效果在这几个层面的习题设置时始终贯串“赵爽弦图”这根主线
微课中的B层习题有意识地引入前年的一道中考真题,本道真题采用一题多解,目的就是培养学生思维的灵活性.本题乍看图形不简单,没有已知相关的数据,后面要求的是两个正方形的面积之比.同学们的常规思维会去求相应的边长,再结合面积公式求解,朝着这个方向走下去会走进“思维迷宫”.为了有效避免这种情况,微课中结合题型特征,以及前面“赵爽弦图”图形结构特征的铺垫,讲解时先由学生惯性思维“想知道边长又不懂得”,借势引入了赋值法,再结合三角形相似求出相应边长间的比例,最后结合“赵爽弦图”中面积的特征顺利解出二者的面积之比.
C层的例题是在前面两个层面例题的基础上在思维层面有所提升.在解决部分正方形问题时,学生需要在深刻理解“赵爽弦图”的模型下,利用“赵爽弦图”结构本身的特殊性,通过补全弦图进行解答,从而使问题得以快速解决.当然,在录制完本微课时,笔者自认为在讲解C层例题时思维的引导还是不够,对于怎样想到添加辅助线,构造“赵爽弦图”解题,为什么要这么操作的讲解还是不够细致,若在这方面思维引导得更加到位,效果应该会更好.
(三)微课教学与数学文化齐飞
数学,显性的是知识、模型和逻辑,隐性的是思想与方法,其背后蕴含的是丰富多彩的数学文化本微课最大的亮点是对数学文化的渗透,开始时教师先介绍高考考试大纲对数学文化的重视,由此让学生对考纲有了进一步的认识同时,为了让学生深入理解数学文化的内涵,引领学生走上数学大道,微课中详细介绍了赵爽相关信息正如张奠宙先生所说过的,“当我们真正地把数学文化的魅力渗入教材、到达课堂、融入教学时,数学就会更加平易近人,让大家通过文化层面易于理解数学、喜欢数学、热爱数学”美中不足的是本微课除了直观呈现“赵爽弦图”之外,在现代信息技术方面的应用应该继续深挖
四、结束语
“赵爽弦图”作为中国数学界的图腾,经典且久远本节微课通过一题多变,一题多解,结合数形结合思想、方程思想、从特殊到一般等常见的数学思想,感受到逻辑思维、图形几何直观、数学运算等数学核心素养这些都是课程改革中强调需要具备的素养,因此,我们要好好欣赏“赵爽弦图”,提升数学文化底蕴

