GeoGebra辅助棱锥的外接球教学案例
徐 敏
(江西省莲花中学,江西 萍乡 337100)
一、引 言
《普通高中数学课程标准(2017年版2020年修订)》的颁布实施,明确提出了鼓励学生运用信息技术学习、探索和解决问题GeoGebra动态软件在演示中不仅有“形”的动态变化,且有对应的“数”的变化,数形结合思想是高中的重要的思想方式.GeoGebra软件兼备几何、代数、概率与统计、微积分、动画动态展示等功能,是适合师生自主探究,互动交流的动态软件.GeoGebra在数学教学中的应用越来越广泛.
基于高中数学核心素养下,对GeoGebra动态几何软件与高中数学相关知识融合的课堂教学案例的研究,构建现代教育技术与高中数学的纽带,为课堂教学提供丰富多样的呈现方式.以GeoGebra辅助多面体外接球教学案例,让学生直观地感受高中数学六大核心素养中的直观想象、数学抽象、数据分析的能力,感受现代科学技术与高中数学的融合带来的课堂教学成果和独特优势,让学生做到学以致用.本文以GeoGebra辅助教学,主要探讨解决棱锥外接球常见的两种方法,即补形法和一般方法(确定球心法)的教学案例,展现GeoGebra动态软件在数学教学中的应用和解决多面体外接球优势.
二、基本性质
圆的性质:圆的任何一条弦的中垂线经过圆心;
球的性质:经过球的任何一个截面的圆心作该截面的垂线经过球心
三、典例分析
方法一:补形法
特征:存在棱锥一条棱垂直于该棱锥的一个面时,此时使用补形法,一般补形为直棱柱,这样棱锥外界球转化为直棱柱的外接球问题

这是一道关于三棱锥外接球问题,考查了学生的抽象思维能力和空间想象能力,传统教学无法给学生展示动态过程,使得教学不够生动具体,教师讲完这道题后,学生可能对这道题还是一头雾水,不能够理解,也无法想象出具体的情形,教学效果很弱.下面我们采取GeoGebra的3D绘图区来分析这道题,试图解决传统教学上的薄弱问题,同时激发学生学习数学的热情和好奇心,激发他们的学习兴趣.
GeoGebra辅助解题步骤如下:

图1

图2

图3

图4
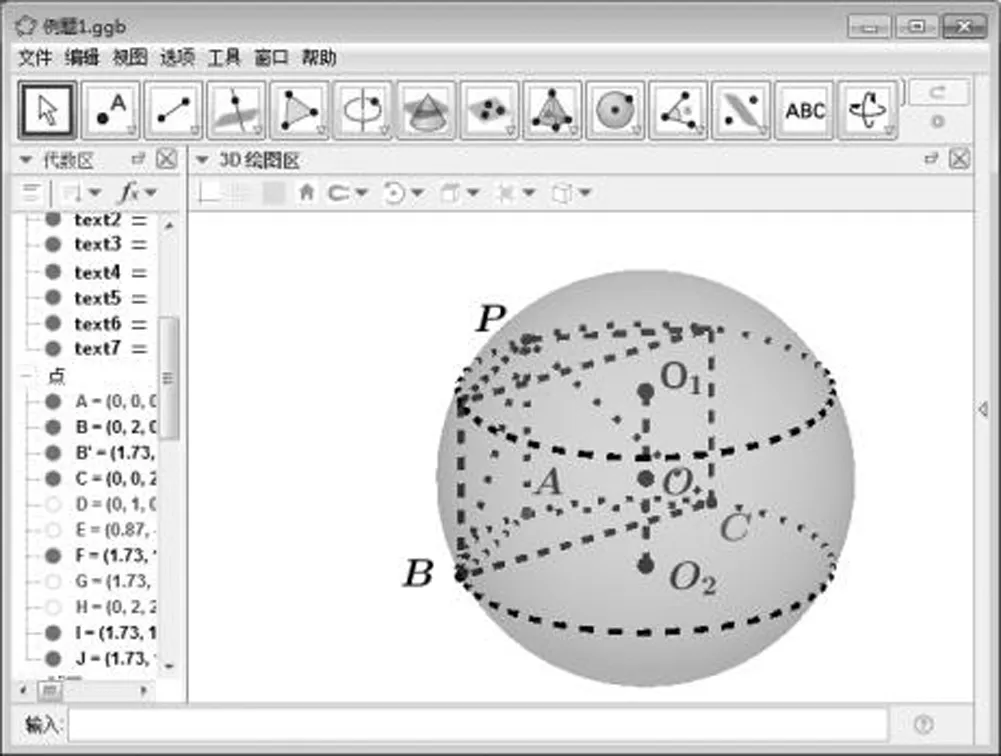
图5
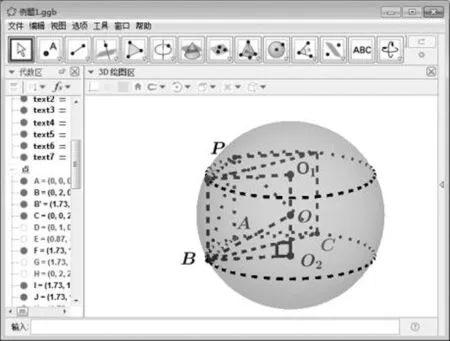
图6





1(2019全国卷Ⅰ)已知三棱锥-的四个顶点在球的球面上,==,△是边长为2的正三角形,,分别是,的中点,∠=90°,则球的体积为( )
分析研究可知,低水头水闸消能效果一般都不很理想,消能率低,闸后水流流速仍然较大,对下游河床及两岸容易形成冲刷,必须采取一定的工程措施才能达到良好的消能效果。通过对普通(单一)消力池、普通(单一)消力池和辅助消能工、复式消力池的消能分析研究,得出如下结论:
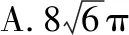
这道高考题同样是一道三棱锥的外接球问题,使用传统教学方式很难展示图形效果,若借助GeoGebra动态软件3D绘图区绘制图像,既能生动形象地解决这道题,又能在教学过程中构建学生的空间想象能力.
GeoGebra辅助解题步骤如下:
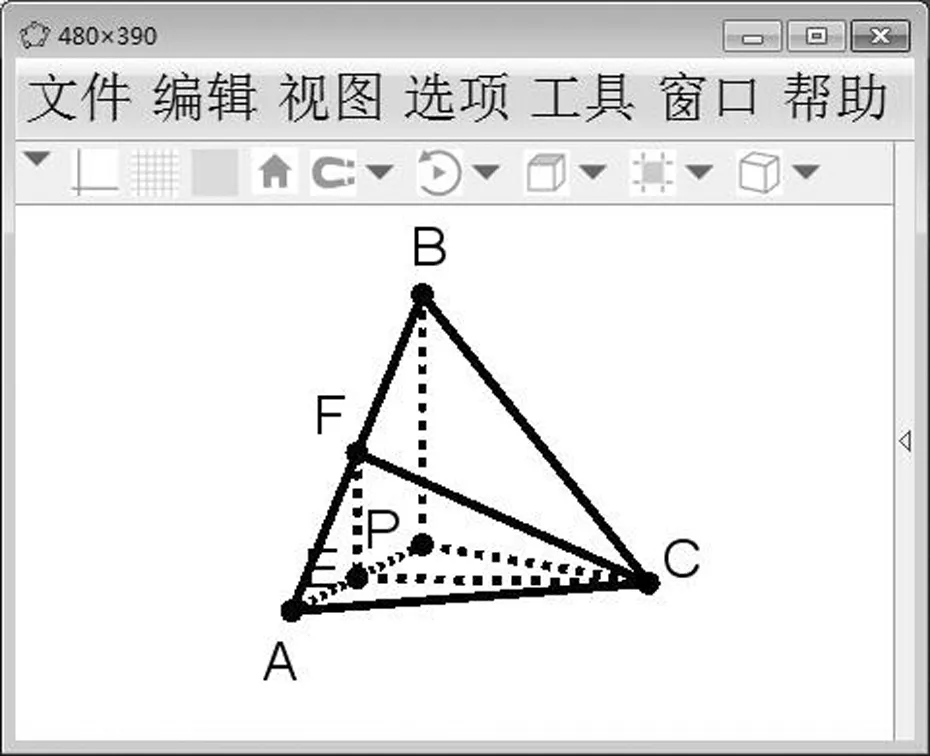
(1)

(2)

(3)
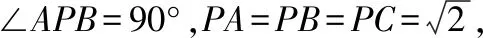
方法二:一般形式(确定球心法)
特征:不能使用补形法解决的棱锥的外接球问题,此时可以通过球的性质确定外接球的球心,得到外接球的半径,从而在相应的直角三角形中计算出半径的值
2已知三棱锥-中,△与△是边长为2的等边三角形,且二面角--为直二面角,则三棱锥-的外接球的表面积为( )

我们通过对题目条件分析可知不能使用补形法,现使用确定球心法来解决问题,GeoGebra软件辅助教学过程如下:

图8

图9
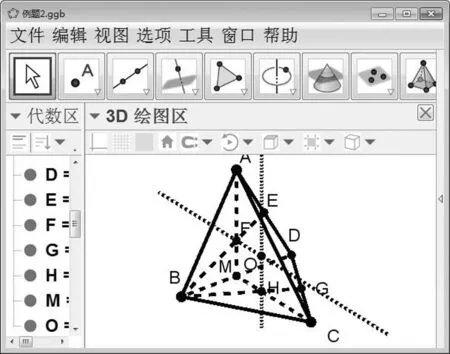
图10

图11

图12





2已知等腰直角三角形中,==2,,分别为,的中点,沿着将△折成直二面角(如图13),则四棱锥-的外接球的表面积为________
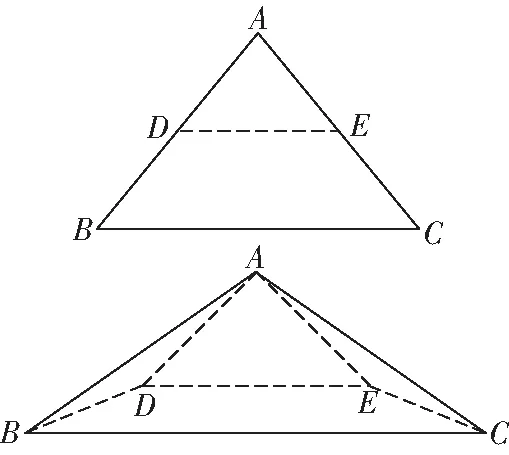
图13
通过对题目条件分析可知不能使用补形法,现使用确定球心法来解决问题,GeoGebra软件辅助教学过程如下:

(1)

(2)

(3)
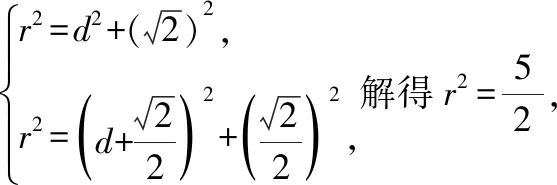
四、结束语
通过以上几个GeoGebra辅助教学典例,我们可以看出,使用GeoGebra动态软件辅助数学课堂教学,能够将抽象的知识用直观的图像表示出来,将抽象的图像转换为动态的直观图像,3D绘图区可以让学生多角度观看立体几何图像,让学生在理解上更加直观通透,达到传统教学无法达到的课堂效果,极大地提升了课堂教学效果和教学质量.

