工程数学课程中几个思政案例分析
翟亚利 艾小川 冯 杭
(海军工程大学基础部,湖北 武汉 430033)
习近平总书记在全国高校思想政治工作会议上指出,“要用好课堂教学这个主渠道”“其他各门课都要守好一段渠、种好责任田,使各类课程与思想政治理论课同向同行,形成协同效应”课程思政是贯彻习主席教育思想的重要举措,高等院校教育要推进课程思政建设,就是要在教育教学和实践训练中坚决落实习近平总书记关于教育的重要论述工程数学课程是大学本科学生需要学习和掌握的一门基础数学课程,与后续专业课程的学习和工程应用密切相关,工程数学课程具有受众面广、学时长的特点,应尽快推进课程思政建设,积极响应习近平总书记号召,加强政治引领,把思想政治教育贯穿育人全过程本文对工程数学课程的几个思政案例进行分析和探讨
1 课程思政在工程数学课程中的体现形式
课程思政建设是落实立德树人根本任务的战略举措,必须将价值塑造、知识传授和能力培养三者融为一体不可割裂针对传统的工程数学课堂教学注重知识传授和能力培养,而轻视学生价值观引导这一实际状况,课程思政建设要求教师们注重课程的育人功能,将思政元素有机融入课堂教学中,达到润物无声的育人效果
在工程数学课程教学中进行课程思政就是要在知识传授中呈现思政元素,因此,挖掘思政元素并进行课程设计是有效进行课程思政教育的前提课程设计要以课程教学计划为基础,对思政元素进行一定的简化和整理,在塑造学生价值的过程中,既要便于学生理解且不增加学生的学习负担又要控制时长不增加教学学时
在工程数学教学过程中,常见的思政元素是数学家们在艰苦条件下对数学发展作出的贡献,特别是中国数学家们的贡献,以此激发学生的学习兴趣,可以增强学生的学习主动性,使学生明确科学需要创新力,培养学生善于思考、勇于创新的精神,进一步培养学生的爱国热情,使学生为祖国感到自豪如,华罗庚(1910—1985)只有初中学历,由于感染风寒导致腿部落下残疾,但他通过刻苦自学成为世界级的数学家、多国科学院院士,深耕解析数论、矩阵几何学、多复变函数论、偏微分方程等领域,在中华人民共和国成立60周年时被评选为“100位新中国成立以来感动中国人物”之一陈省身(1911—2004)是中国第一个自己培养的数学研究生,毕业于南开大学,获清华大学理学硕士学位、汉堡大学理学博士学位,他的贡献主要包括给出高维Gauss-Bonnet公式的内蕴证明,提出陈氏示性类,发展了纤维丛理论,建立了高维复流行上的值分布理论等,他是20世纪最伟大的几何学家之一,被誉为现代微分几何的奠基人吴文俊(1919—2017)年少时以“拓扑地震”成名国外,他在拓扑学的示性类和示嵌类方面进行了奠基性的研究工作,这项研究在拓扑学中具有承前启后的作用吴文俊在年近花甲之时开创了数学机械化领域,在中华人民共和国成立70周年时被授予“人民科学家”的荣誉称号
除了介绍中国数学家、世界数学家在相关知识领域的贡献,教师也可以结合热点和生活实际撰写合适的案例,通过案例达到育人的目的
2 思政案例分析
2.1 矩阵乘法与大国工匠精神
案例:甲方需要向乙方传输一张具有军事特色的图片——飞机,出于保密和经济方面的考虑,需要对图片进行加密传输如何对图片进行加密呢?
案例分析:
图片加密的方法有很多,比较常用的方法就是通过矩阵乘法来加密,可以通过将飞机图片隐藏在常见的图片中进行传输比如,将飞机图片隐藏在校园建筑物图片中
案例求解:
借助Matlab软件,读取需要传输的飞机图片和校园建筑物图片,并截取建筑物图片和飞机图片具有相同的像素的部分.分别用飞机图片的红绿蓝三原色数据乘密钥矩阵,进而将变换后的三原色数据矩阵合并为图片数据,将合并后的数据与校园图片数据相加就可以得到加密后的图片数据.在这一过程中涉及的Matlab语句有:imread、size、cat、imshow、double、int.
飞机图片、校园建筑物图片、加密后的图片如图1所示

图1
信息隐藏案例的分析可以让学生感受到数学知识在实际生活和工作中的应用,提高学生的学习兴趣在学习和工作过程中,哪些信息需要隐藏呢?比如,学生进行了学术研究或开展了相应的试验研究但还没有撰写学术论文、企业的核心技术、国家在某方面取得的新成果等教师要引导学生,让学生明白科学研究的方向和内容不分大小,在社会发展进步的任何一个方面,都需要一些潜心研究、甘于寂寞、甘于奉献的人,为祖国不断强大贡献自己的一份力,从而培养学生的大国工匠精神
2.2 正态分布与分级评价
在论文评审中经常采用等级评价的方式,通常情况下一篇论文会由多位评审专家进行评审,根据评审结果对论文进行综合评价
案例:现得到三位评审专家对甲、乙、丙三篇论文的评价结果,见表1所示
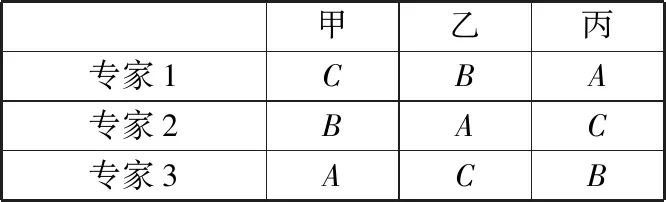
表1 三位专家对三篇论文的评审结果
如何根据三位专家的评审结果对这三篇论文的优劣进行排序
案例分析:
由以上评审结果很难对这三篇论文的优劣进行排序,所以,我们需要搜集更多的三位专家的论文评审结果,一方面,专家打分具有一定的个人偏好,可通过大量信息分析专家在论文分级评价过程中的个人偏好;另一方面,每一名专家打分受到个人认知水平、个人对评分标准的理解、个人对参评论文的要求等多种因素的影响,其打分服从正态分布因此使用正态分布结合搜集到的信息将等级转化为数值分这样就可以使用数值分对三篇论文进行排序
案例求解:
现搜集到三位评审专家对相同的40份论文的评价结果,如表2所示

表2 三位专家对40份论文的评审结果
由表2可知,直观上,专家1的要求更高一些,因为被专家1评为的论文份数最少下面将表2使用正态分布将等级转化为数值分
先在标准正态分布下计算每一位专家各个等级分对应的数值分,对于某等级选择使得两侧的概率相等的数来表示该等级的分值由表2可知专家1评等级的分值满足

查标准正态分布表得=1285专家1评等级的分值满足

查得=0065专家1评等级的分值满足

查得=-115
类似地,专家2的三个等级对应的数值分为0935,-0155,-1215,专家3的三个等级分对应的数值分为 104,-0155,-1355
由此得到,甲的论文得分情况为-115-0155+104=-0265,乙的论文最后得分为-0355,丙的论文最后得分为 -0085,通过比较大小可知三篇论文分值从高到低的排序为丙、甲、乙
案例分析不仅可以提高学生的学习兴趣和学习主动性,而且可以让学生感受到概率论在现实生活中的广泛应用,使用数学知识研究事物的内在规律,认识现象所蕴含的事物本质同时,这个案例分析,让学生明白,在学习、工作、生活中碰到困难时,应该寻找科学的、有说服力的依据,使用科学的方法挖掘现象所掩盖的事实,通过摆事实、讲道理解决矛盾和困难
2.3 期望与新冠肺炎核酸检测方案
受新冠疫情的影响,某一地区在连续出现本土确诊病例且该确诊病例在潜伏期活动范围比较广的情况下,通常需要对该地区人员免费进行全员核酸检测,为了节约核酸检测成本并提高检测效率,经常采用混合样本检测的方式这一行为就可以使用概率论中随机变量的数学期望进行解释
案例:假设由于防疫需求需要对某地区进行全员核酸检测,该地区的人口总数为,市民感染新冠肺炎(即核酸检测结果为阳性)的概率为,计划采用个人混合样本的检测方式进行检测,应该如何确定,此时检测工作量的效率如何?
案例分析:
采用个人混合样本的检测方式,则在未感染的情况下平均每个人的核酸检测次数为1,若个人中有一个人感染,则需要对这个人中的每个人再单独进行一次核酸检测,因此每个人进行核酸检测的次数可以看作随机变量,通过计算随机变量的期望,在平均检测次数最小的优化目标下确定的大小
案例求解:
设每个人核酸检测的次数为随机变量,该地区核酸检测结果为阳性的概率为,则核酸检测结果为阴性的概率为=1-,个人混合样本呈阴性的概率为,个人混合样本呈阳性的概率为1-则为二项分布,其分布律如表3所示

表3 随机变量X的分布律
由离散性随机变量期望的计算公式计算得到每个人的平均检测次数为

由于进行核算检测的总人数为,则该地区进行核算检测的平均总次数为
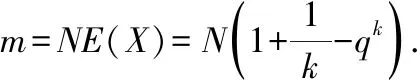
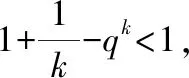

从理论上来分析,在对未感染概率有一定了解的条件下,应该选择使得()达到最小的,此时混合样本的样本数可以使得检测费用和检测效率达到最大而实际上,受到人员组织、现场管理、样本混合充分性、取样试管的大小等多方面因素的影响,通常需要结合实际确定混合样本的人数
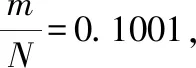
在生活实际中,政府机关与医学部门的工作人员会综合考虑,在充分利用现有资源的基础上提出合适的检测策略达到防疫效果和效益的最大化,比如,对于感染概率偏大的地区,有些地区采用4人混合样本的采样方法市民要充分相信职能部门的科学决策,积极主动配合各项决定和政策,将个人防疫安全与大环境防疫安全融为一体,要明白只有大环境安全自身才能安全的道理
2.4 极大似然估计与水雷引信设置
背景介绍:某型号水雷的引信为综合引信,其中声引信主要通过获取目标行驶过程中的声音强度等相关信息进行综合判断,并决策水雷是否发生动作因此,在引信上有安装声接收装置,用来接收目标行驶过程中发出的声音信号
在这一过程中需要解决两个问题:目标物体声音信号的分布情况,以及水雷声引信在什么情况下动作
围绕第一个问题设置案例一
案例一:某外军舰船经常在我国海域附近活动,水下测量系统可测得其声音信号假设测得的舰船在某频段上的20个声音信号数值见表4所示在工程上一般认为,一段时间内测量得到的目标声音信号值服从正态分布,如何根据所测得的目标声音信号估计正态分布中的参数呢?

表4 目标声音信号值
案例分析:
舰船声音为其动力机械(主机、辅机、螺旋桨、推进系统等)和辅助机械(泵、风机等)在运行时发出的声音,虽然可以通过声源控制、传递途径控制、使用接收器噪声防护设备等方法进行声音控制,但是很难做到完全消除此外,长期的实践经验表明,自然现象和社会现象中,大量随机变量都服从或近似服从正态分布一般来说,若影响某一数量指标的随机因素很多,这些因素相互独立且每一个因素所起的作用又不太大,则这个指标可认为是服从或近似服从正态分布因此,案例中一段时间内测量得到的目标声音信号值服从正态分布的假设是合理的
案例求解:
假设舰船的声音信号为随机变量,由工程实际有~(,),其中,为正态分布的均值,为正态分布的方差,均值和方差均未知设测量得到的个舰船声音信号值为,…,
这是一个含有2个未知参数的连续型随机变量,采用极大似然估计法估计未知参数

按照极大似然估计的步骤,第一步写似然函数

第二步,求似然函数的最大值点先对似然函数取对数,得到对数似然函数

由于含有2个未知参数,对数似然函数分别对未知参数,求偏导,得到对数似然方程组

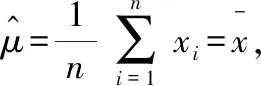
若以案例一中的舰船为打击目标,其声音信号的分布情况可以为水雷声引信的设计提供依据这就是前面提到的第二个问题:水雷声引信在什么情况下动作
案例二:水雷声引信的设计要求之一是合理设定动作参数动作参数是指水雷声引信动作所需的目标声音信号的最小值在设计动作参数时,需考虑目标漏检(目标声音信号小于)的情况,假定要求漏检的概率不超过0005,又设在一段时间内目标声音信号服从参数未知的正态分布,应该如何来设计水雷声引信的动作参数呢?
案例分析:

案例求解:
假设目标声音信号为随机变量,~(,),其中和为正态分布的未知参数


本案例设计为复合案例,涉及多个参数估计的方法和步骤、极大似然估计的不变性、正态分布的标准化等多个知识点,通过案例式教学可以让学生体会到如何将实际问题转化为数学问题进行分析和求解,提高学生的学习兴趣和学习主动性此外,该案例设计与军事内容相关,使学员更好地理解数学知识与军事问题的联系,深刻体会数学的“无处不在”,塑造学员的抽象思维能力、定量思维能力、逻辑推理能力和创新意识,增强“四个自信”
3 结 语
工程数学是大学本科的一门基础数学课程,具有受众面广、学时长、与工程实际联系紧密的特点,在该课程中进行课程思政教育具有紧迫性和可行性工程数学课程思政建设要达到“润物无声”的效果,需要从数学家在数学中的贡献、数学案例分析等环节入手,本文对几个思政案例进行了分析和总结,为工程数学课程思政建设奠定基础

